基于QPSO聚类算法的图像分割方法

王丹　周锦程

【摘 要】量子粒子群优化算法克服了传统粒子群优化算法中无法保证全局收敛、容易陷入局部最优的缺点，是近年来优化技术领域的一个研究热点。本文结合当前图像分割中常用的K-均值聚类算法中的相关技术，设计了基于QPSO的聚类算法并将其用于图像分割处理问题中。实验结果表明：在图像分割处理中，相对于K-均值聚类算法，QPSO聚类算法不仅不依赖于初始聚类中心的选择，而且还能得到相对于K-均值聚类算法精度更高的聚类中心，其在图像分割中的效果优于通常的K-均值聚类算法。

【关键词】PSO算法；QPSO算法；K-Means聚类；图像分割

【Abstract】The quantum particle swarm optimization（QPSO） algorithm overcomes the shortcomings of the traditional particle swarm optimization algorithm which can not guarantee the global convergence， easy to fall into the local optimal. QPSO algorithm has become a research hotspot in the optimization technology filed in recent years. In this paper， combined with the relevant technology of the current commonly K-Means clustering algorithm in the image segmentation problem， we propose a new QPSO based clustering algorithm and we use it to the image segmentation filed. Experimental results show that， with respect to the K-means clustering algorithm， QPSO clustering algorithm does not rely on the choice of the initial cluster center， but compared with the K-means clustering algorithm， it can get higher precision clustering center. Thus， it is better than the usually K-means clustering algorithm in the image segmentation problem.

【Key words】PSO Algorithm； QPSO Algorithm； K-Means Clustering； Image Segmentation

0 引言

群体智能算法是基于群体行为对给定目标进行寻优的一种启发式搜索算法，自20世纪80年代出现这类算法以来，已经得到了众多研究人员的广泛关注，并已发展成为优化技术领域的一个热点研究方向。粒子群优化（Particle Swarm Optimization，PSO）算法[1]是一种典型的群智能优化算法，该算法于1995年由美国社会心理学家Kennedy博士和电气工程师Eberhart博士在对社会型生物群体行为模拟的基础上提出。由于PSO算法计算简单、控制参数较少且易于实现，因此已被广泛应用于各种优化计算领域[2-4]。因为PSO算法通常无法保证收敛于优化问题的全局最优解甚至于局部最优解[5]，因此，国内学者孙俊等人受量子力学等相关理论的启发，利用量子测不准原理来描述粒子的运动状态，并在PSO算法基础上提出了具有量子行为和全局收敛性能的量子粒子群优化（Quantum-behaved Particle Swarm Optimization，QPSO）算法[6]，该算法认为处于量子束缚态的粒子可以以一定的概率密度出现在空间中的任何点，粒子可以在整个可行空间中进行搜索且不会发散到无穷远处。

在图像处理的研究中，人们通常会关注图像中的某些局部内容，如目标或者前景，以便进行后续的图像处理，这种把图像分成若干个特定的、具有独特性质的区域并提取出感兴趣的目标的技术和过程，称为图像分割。图像分割是图像分析的重要环节，经过图像分割所提取出的目标可以广泛应用于图像的语义识别、图像搜索等众多领域。

1 相关概念

1.1 标准PSO算法

由Kennedy和Eberhart所提出的PSO算法，其主要思想来源于对鸟类群体行为的研究。在利用该算法解决优化问题的过程中，首先是要初始化一组随机解，然后通过迭代方式来搜寻最优值。在PSO算法中，每个优化问题的解都被看做搜索空间中的一只鸟，称为“粒子”。所有的粒子对应着优化问题的适应值，粒子的速度决定了其飞行的方向和距离，粒子通过追寻群体中的最优粒子来完成解空间的搜索，其具体的算法原理描述如下：

1.2 QPSO算法

由于PSO算法不能收敛于全局最优解，甚至局部最优解[5]，许多学者提出了大量的方法以改进PSO算法的收敛性能，但实际情况表明，很多方法对PSO算法的改进是有限的。孙俊等人在研究了Clerc等人关于收敛行为的研究成果后，从量子力学的角度出发，提出了具有量子行为的粒子群优化算，即QPSO算法[6]。在该算法中，由于其采用了量子测不准理论，因此粒子的位置和速度不能同时被精确测定，但由波函数的统计意义，可以通过波函数给定的概率密度函数来确定粒子在某个时刻出现的概率，该算法原理描述如下：

1.3 K-均值聚类算法

K-均值聚类算法又叫K-Means聚类算法，其算法原理是：首先随机地从数据集中选取K个点作为初始聚类中心，然后计算各个样本到聚类中的距离，把样本归到离它最近的那个聚类中心所在的类；然后计算新形成的每一个聚类的数据对象的平均值来得到新的聚类中心，如果相邻两次的聚类中心没有任何变化，说明样本调整结束，聚类准则函数已经收敛。K-均值聚类算法的一个特点是在每次迭代中都要检查每个样本的分类是否正确，若不正确，则需进行调整，待全部样本调整结束后，再修改聚类中心，进入新一轮的迭代。如果在迭代过程中，所有的样本均被正确分类，则聚类中心不会再有变化，这标志着算法已经收敛。K-均值聚类算法的算法流程可以描述如下：

Step 1 从n个数据对象任意选择k个对象作为初始聚类中心。

Step 2 根据每个聚类对象的均值（中心对象），依据距离公式（8）计算每个对象与这些中心对象的距离；并根据最小距离重新对相应的对象进行划分。

Step 3 按照公式（9）重新计算每个（有变化）聚类的均值（中心对象）。

Step 4 计算误差平方和准则函数（10）的值，判断是否满足算法结束条件，若满足，则算法结束。否则循环Step 2到Step 3，直到满足算法结束条件为止（即每个聚类不再发生变化，或达到最大迭代次数）。

2 基于QPSO聚类算法的图像分割

2.1 QPSO聚类算法的图像分割流程

K-均值聚类算法是当前流行的基于图像颜色的图像分割方法，在进行QPSO算法聚类分割时，受K-均值聚类算法的良好性能的启发，我们采用K-均值聚类算法中样本到聚类中心的距离作为QPSO算法中聚类的度量标准，即：

Step 1 提取图像的RGB通道的灰度级强度作为特征向量。

Step 2 初始化（聚类中心、个体最优解、全局最优解）。

Step 3 根据式式（11）计算聚类，根据式式（12）计算个体的适应度函数值。

Step 4 计算并更新粒子群的平均最好位置mbest，更新个体最好位置pbest和全局最好位置gbest。

Step 5 根据式（6）计算随机点p。

Step 6 根据式（7）更新粒子的中心向量。

Step 7 重复Step 2至Step 6，直到满足迭代结束条件或最大迭代次数为止。

3 实验结果

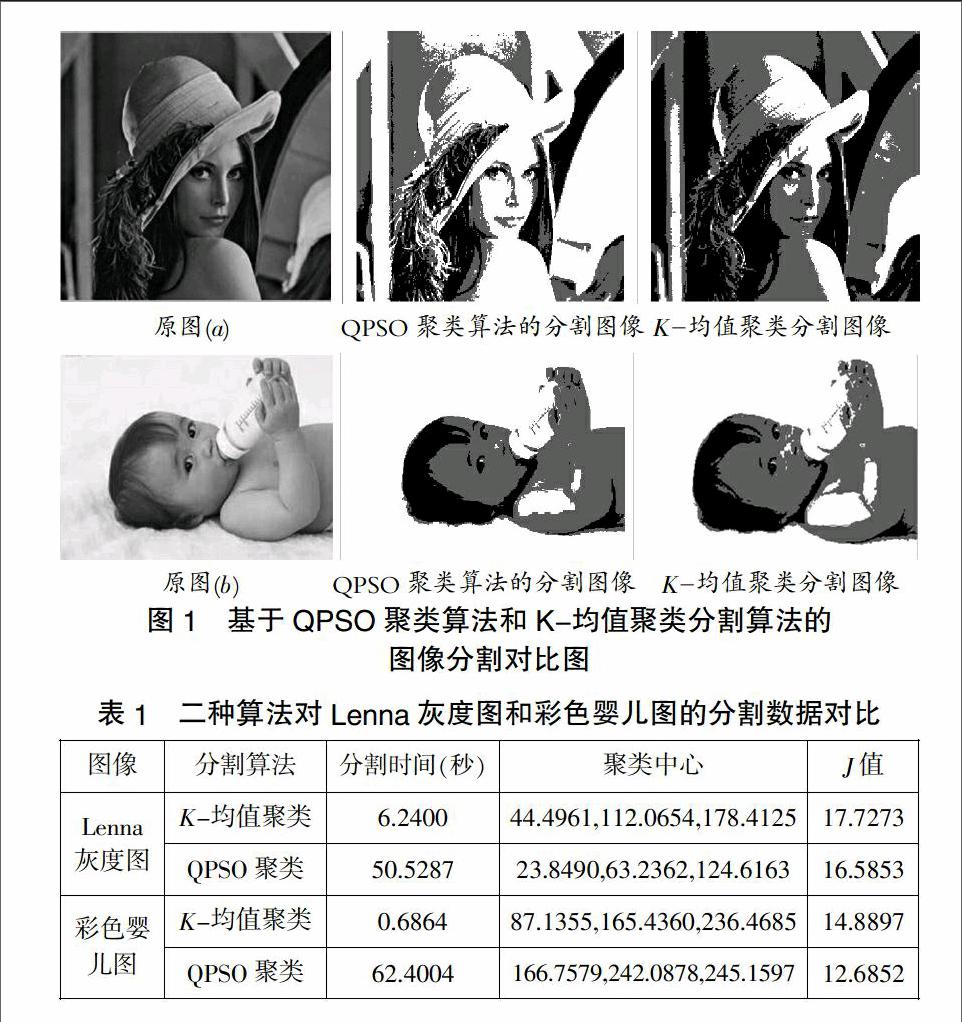
为验证基于QPSO聚类算法的图像分割性能，我们分别采用基于QPSO聚类算法和K-均值聚类分割算法对255×255的Lenna灰度图和250×350的彩色婴儿图进行实验对比分析，实验环境选用AMD Athon 645 4核3.10GHz处理器，内存为4GB的PC机，其分割结果如图1所示：

通过对以上两组分割结果图像的对比，我们看到QPSO聚类算法和K-均值聚类算法对原图（a）和原图（b）进行的图像分割都取得了比较良好的效果，且基于QPSO聚类算法的图像分割结果轮廓更为清晰，层次更为分明。

表1给出了二种算法对Lenna灰度图和彩色婴儿图分割的对比数据，从表1可以看出，K-均值聚类算法在分割时间开销上相对于QPSO聚类算法有着一定的优势，且基于QPSO聚类算法在分割Lenna灰度图和彩色婴儿图中，其误差平方和项对应的J值均小于相应的K-均值聚类算法。此外，由于K-均值聚类算法对初始聚类中心的选取至关重要，若选取不得当，可能会大大增加聚类的时间开销，甚至在一定的迭代步内可能无法得到满足精度要求的解。而QPSO聚类算法对初始聚类中心没有任何要求，且其可以得到比K-均值聚类算法精度更高的聚类中心。

4 结语

受K-均值聚类算法的启发，我们设计了基于QPSO的聚类算法来处理图像分割问题。实验结果表明，相对于K-均值聚类算法，QPSO聚类算法在不需要选择适当的初始聚类中心的情况下也能够获得精度比K-均值聚类算法更高的聚类中心，且基于QPSO聚类算法的图像分割方法比K-均值聚类算法的图像分割得到的分割图像轮廓更为清晰，层次更为分明。

【参考文献】

[1]Kennedy J， Eberhart R C. Particle swarm optimization[C]. IEEE International Conference on Neural Networks，1995， 1942-1948.

[2]Cohen S， de Castro L N. Data clustering with particle swarms[C]. IEEE Congress on Evolutionary Computation， 2006： 1792-1798.

[3]Lope H S， Coelho L S. Particle swarn optimization with fast local search for the blind traveling salesman problem[C]. Fifth International Conference on Hybrid Intelligent Systems， 2005： 245-250.

[4]Nenortaite J， Simutis R. Adapting particle swarm optimization to stock markets[C]. Proceedings 5th International Conference on Intelligent Systems Design and Applications， 2005： 520-525.

[5]Van Den Bergh F. An analysis of particle swarm optimizers[D]. University of Pretoria， 2006.

[6]Sun J， Feng B， Xu W. Particle swarm optimization with particles having quantum behavior[C]. IEEE Congress on Evolutionary Computation， 2004： 325-331.

[责任编辑：杨玉洁]