一种雷达伺服系统的复合控制策略

官伯林

【摘 要】雷达伺服系统的控制策略，能够直接影响雷达探测范围、跟踪精度、实时性、稳定性等性能指标，是制约雷达系统性能的关键之一。为改善雷达伺服系统的控制性能，提高系统的稳定性和鲁棒性，提出一种复合控制策略。在详细分析雷达伺服系统动力学特性的基础上，建立了雷达伺服系统的动力学数学模型；然后基于该数学模型，设计出一种基于迭代学习控制和模糊PID控制的复合控制策略，应用模糊PID控制以提高伺服系统的动态性能和鲁棒性，应用迭代学习控制以提高伺服系统的稳态精度。仿真结果证明，所设计的复合控制能够保证雷达伺服系统的稳定性，而且控制精度高，鲁棒性好，控制性能良好；因而能够有效地提高雷达系统的性能，具有良好的实际应用价值。

【关键词】雷达伺服系统；复合控制；迭代学习控制；模糊PID控制

【Abstract】The control strategy of radar servo system is one of the key factors that limit the performance of radar system， which can affect the radar coverage， tracking accuracy， real-time， and stability. For improving the control performance of radar servo system， the compound control system is built. Through the dynamic analysis， the dynamic model of system is build， and the compound control strategy is designed based on iterative learning control theory and fuzzy PID control theory. Fuzzy PID control theory could improve the dynamic property and the robustness of system， and iterative learning control theory could improve the stability accuracy of system. The result of simulation proves the validity of compound control strategy， which could keep the stability of system， and improve the control accuracy and robustness of system. Then the compound control strategy can improve the performance of radar system， and could be applied in practice.

【Key words】Radar servo system； Compound control； Iterative learning control； Fuzzy PID control

0 引言

随着雷达技术的迅速发展，特别是软件化和通用化等新概念雷达的提出，对雷达伺服系统控制精度的要求越来越高。同时，作为雷达重要组成部分的伺服系统，其控制技术是制约雷达系统探测和跟踪性能的关键之一[1，2]，对于雷达探测范围、跟踪精度、系统实时性和快速性等雷达性能的影响是不可忽略的[3，4]。

然而目前雷达伺服系统的控制策略设计中，仍然以PID控制为主[5]。PID控制虽然算法简单；但是PID参数调试过程繁琐，效率低；而且PID控制局限于线性系统，鲁棒性差；同时PID参数值虽然有一定局域性的优化值，但非全局的最优值。

因此，单一的PID控制已无法满足雷达新技术研究和发展的需求[6，7]；必须设计新型的雷达伺服系统控制策略，以提高雷达伺服系统的控制稳定性和控制精度，改善雷达系统的综合性能[8，9]。

现有的各类控制算法当中，迭代学习控制算法简单，不依赖于系统的精确数学模型，同时学习能力强，只需较少的先验知识，即可以非常简单的方式处理不确定度相当高的非线性强耦合动态模型；模糊PID控制既具有模糊控制灵活而适应性强的优点，又具有常规PID控制精度高的特点， 对被控对象的时滞、非线性和时变性具有一定的适应能力等优点，同时对噪声也具有较强的抑制能力，鲁棒性强。

因此，本文提出一种将迭代学习控制和模糊PID相结合的新型复合控制策略；然后，将此策略应用于雷达伺服系统的控制当中，通过仿真实验，以验证所设计的复合控制策略的有效性和实用性。

1 雷达伺服系统数学模型

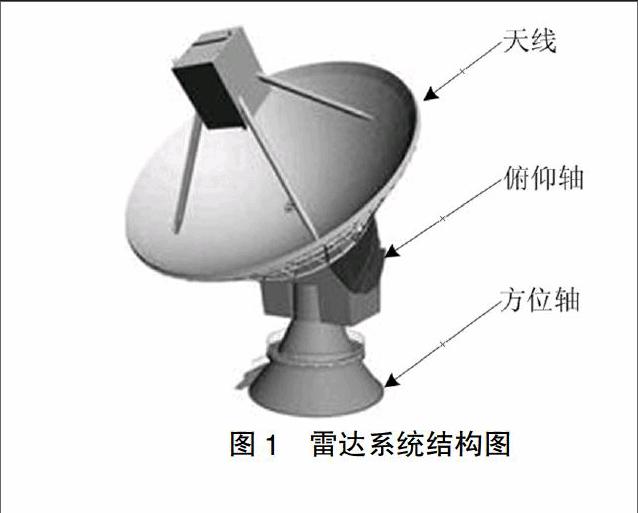
雷达系统结构如图1所示，方位轴和俯仰轴通过力矩电机驱动，从而带动雷达天线转动。通过系统中方位轴和俯仰轴的动能、势能和磁能分别进行分析，可以建立雷达伺服系统的机电动力学模型：

（1）动能：方位动能Tφ只有绕方位轴的转动动能；俯仰动能Tθ包括两部分，即绕方位轴的转动动能和绕俯仰轴的转动动能；电机转子动能Tm包括方位电机和俯仰电机的动能。

（2）势能：设大地坐标轴的原点为零势能点。系统势能V包括重力势能和方位、俯仰传动链的等效弹性势能。

（3）磁能：磁能W主要由方位、俯仰伺服驱动电机的磁能产生。

（4）耗散能：耗散能F包括按线性阻尼模型考虑系统的耗散能，以及各转动轴电机和传动链的耗散能。

通过以上分析，可以得到雷达伺服系统的Lagrange函数为：

2 雷达伺服系统的复合控制策略

基于迭代学习控制和模糊PID控制的复合控制策略原理如图2所示，其中，迭代学习控制器用于消除死区、非线性等外界扰动，模糊PID控制器用于改善系统响应速度，提高系统控制精度。

图2中，rd（t）为期望输出值，ek（t）为跟踪误差，yk（t）为实际输出值，uk（t）为控制信号，ukf（t）为前馈环控制信号，ukb（t）为反馈环控制信号。

2.1 模糊PID控制器设计

模糊PID控制器原理如图3所示，定义系统误差e，误差变化ec和PID控制kp、ki、kd的模糊子集均为：{NB， NM， NS， ZO， PS， PM， PB}，控制系统隶属度函数图如图4所示。kp/ki/kd自适应模糊整定规则表如表1所示。

设PID参数初始值为kp0、ki0、kd0，则模糊PID控制器的参数值为：

2.2 迭代学习控制器设计

迭代学习控制分为开环学习算法和闭环学习算法。开环学习算法利用控制系统的上一次运行的信息，迭代周期较长，而且容易出现发散现象；闭环学习算法利用控制系统的当前运行信息，同时舍弃上一次的运行信息，具有更好的跟踪性能和抗干扰性。因此，本次设计采用闭环PID学习算法，如下式所示：

3 仿真实验和分析

为验证所设计的复合控制策略的有效性，将其应用于雷达伺服系统的控制当中，通过仿真实验进行验证。

首先，根据对雷达伺服系统的动力学数学模型分析可知，若不考虑系统方位轴和俯仰轴之间存在的耦合关系、参数不确定性和外界扰动，则对于方位、俯仰两个传动子系统，均可以简化为二阶传动模型：

因而在控制器设计中，把雷达伺服系统各转动轴之间存在的耦合关系、参数不确定性和外界扰动等不确定因素均作为干扰w，以简化控制系统数学模型，降低控制系统分析和控制器设计难度。

因此，雷达伺服系统的复合控制中，可以将方位轴和俯仰轴均简化为二阶传动系统，分别设计复合控制器，其控制系统结构如下图所示：

为验证所设计控制器的有效性，选取典型的阶跃响应曲线和正弦响应曲线，应用复合控制策略进行仿真测试，并与模糊PID控制和PID控制相比较，以验证本文所设计控制策略的控制性能。

图6和图7分别给出了三种控制器对雷达伺服系统的阶跃响应控制仿真曲线（各转动轴转角阶跃为α=0.5rad）和正弦响应控制仿真曲线（各转动轴正弦幅值为α=0.2rad，周期为T=2.5s）。从图6和图7的控制曲线中可以看出，与模糊PID控制和PID控制相比，本文所设计的复合控制方法，不但能够保证雷达伺服系统的稳定，而且响应速度快，调节时间短，控制误差小，控制精度高。因此，雷达伺服系统的动态响应特性和稳态特性均最为优越，使得系统具有良好的控制性能。

4 结论

本文首先在分析雷达伺服系统动力学特性的基础上，基于Lagrange- Maxwell机电动力学方程，建立了雷达伺服系统的动力学模型，然后根据雷达伺服系统设计的需求，设计了雷达伺服系统的基于迭代学习控制和模糊PID控制的复合控制策略，应用迭代学习控制器消除死区、非线性等外界扰动，应用模糊PID控制器改善系统响应速度，提高善系统控制精度。最后通过仿真实验，以验证所设计的复合控制控制策略的有效性和实用性。

仿真实验结果证明，与其它控制策略相比，应用本文设计的复合控制策略能够保证雷达伺服系统的稳定，而且系统在控制运动过程中的控制误差最小，控制精度最高；同时系统各转动轴的控制调节时间最短，稳态误差最小；因而雷达伺服系统的动态性能指标和稳态特性均最为优越，具有良好的控制性能。综上所述，本文的复合控制策略，设计方法简单，控制精度高，系统的自适应能力和鲁棒性好，具有重要的理论意义和实际应用价值。

【参考文献】

[1]周剑.α-β滤波器和复合控制[J].系统工程与电子技术，2007，29（3）：368-371.

[2]孙丽娜，宋悦铭，戴明.采用复合控制提高机载光电平台的数引跟踪精度[J].光学精密工程，2008，16（2）：265-269.

[3]张远高，杨文光，孙汉青等.两种自动跟踪控制策略的比较[J].火力与指挥控制，2014，39（增刊）：71-73.

[4]贾建芳，李瑞，李江.前馈-模型参考自适应复合控制策略[J].火力与指挥控制，2014，39（12）：135-138.

[5]刘小强，芦峰，梁晓东，等.一种光电复合跟踪控制切入反馈控制的误差抑制方法[J].应用光学，2013，34（1）：51-55.

[6]王小齐，赵振海，李晶娣，等.再生反馈技术在跟踪控制系统中的应用[J].应用光学，2004，25（6）：1-4.

[7]陆培国，寿少峻.健在光电系统高精度跟踪控制技术[J].应用光学，2006，27（6）：480-483.

[8]张柏林，黄建国.目标前馈在精密跟踪雷达中的应用[J].现代雷达，2001（3）：65-68.

[9]罗安，孙景芳.相控阵天线波束指向跟踪算法研究[J].舰船电子工程，2008（1）：32-36.

[责任编辑：汤静]