支付值为语言信息的矩阵对策求解方法

杨靛青，李登峰

(福州大学经济与管理学院，福建 福州　350116)

支付值为语言信息的矩阵对策求解方法

杨靛青，李登峰

(福州大学经济与管理学院，福建 福州350116)

摘要：在阐述语言评估标度定义及其运算法则、 比较规则的基础上，提出了支付值为语言信息的矩阵对策定义及其解的概念，并研究了如何将求解局中人的极大-极小与极小-极大策略问题转化为求解一对辅助线性规划问题. 数值实例表明，所提方法是有效、 实用的，所建立的支付值为语言信息的矩阵对策理论与方法既是对经典矩阵对策理论的发展，又可为解决其他带有模糊语言信息的对策问题提供新的途径.

关键词：语言信息； 矩阵对策； 线性规划； 对策论

0引言

矩阵对策是一类在对抗竞争对策问题中应用比较成熟的对策，主要思想是局中人在有限个策略中根据不同对策局势的支付情况选择最有利自己的策略方案. 目前，支付值为数值的矩阵对策研究已经取得了丰硕的成果[1-12]. 但在一些实际对策问题中，由于对策环境的复杂性、 多样性和不确定性，人们(局中人)对局势结果(或结局)的主观判断可能难以完全用数值精确度量，或数值度量的成本、 技术要求过高，又或者用模糊语言判断便可以满足决策需要. 在这些情形下，局中人对局势结果的判断一般直接用语言形式表达. 例如，将两家电子商务商家在市场竞争中如何提高各自产品的市场份额看作一个对策问题，对策的结果为商家对各个局势下的销售情况的主观判断，用“很高”、 “高”、 “一般”、 “低”、 “很低”等语言术语来评估各局势的销售量. 这类对策问题可用语言信息表示局中人的判断结果，通过建立支付值为语言信息的矩阵对策加以研究解决.

在阐述语言评估标度集及其比较、 运算规则的基础上，着重研究支付值为语言信息的矩阵对策(简称语言值矩阵对策)问题. 首先，给出语言值矩阵对策的定义及其解的概念； 然后，将求解两个局中人的策略问题转化为求解一对辅助线性规划问题. 可为解决复杂模糊信息环境下的竞争决策与对策问题提供新的途径.

1语言评估标度

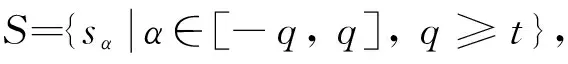
1) 若α≥β，则sα≥sβ，特别若α=β，则sα=sβ；

2) 存在负算子neg(sα)=s-α，特别地，neg(s0)=s0；

3) 若α>β，则max{sα，sβ}=sα和min{sα，sβ}=sβ.

定义1设sα，sβ∈S，λ∈[0，1]，规定：

1) sα⊕sβ=sα+β； 2) λsα=sλα

定理1设sα，sα1，sα2∈S，则

1) sα1⊕sα2=sα2⊕sα1； 2) λ(sα1⊕sα2)=λsα1⊕λsα2(λ∈[0，1])；

3) λ1sα⊕λ2sα=(λ1+λ2)sα( λ1，λ2∈[0，1])

2支付值为语言信息的矩阵对策的数学表示及其解的定义

由于实际竞争性决策问题的复杂性和不确定性，通常很难精确地给定局中人的支付值，而采用语言评估术语相对方便、 简单. 因此, 建立语言评估术语与语言值之间的对应关系，可以方便地描述复杂的竞争性决策问题.

由于局中人之间的利益是根本对立的，因此对于有理智的局中人而言，常遵循“从最坏处着想，从最好处入手”的决策原则. 例如，设S′={s-3，s-2，s-1，s0，s1，s2，s3}，其中语言评估标度的语义为s-3=极低，s-2=很低，s-1=低，s0=一般，s1=高，s2=很高，s3=极高. 局中人P1的语言值矩阵A为:

定义2 若存在混合策略(x*，y*)(x*∈X，y*∈Y)使得对任意x∈X，y∈Y，满足:

E(x，y*)≤E(x*，y*)≤E(x*，y)

则称(x*，y*)是Γ2的混合策略鞍点，x*与y*分别为局中人P1和P2的最优(混合)策略，v=x*TAy*为语言对策值.

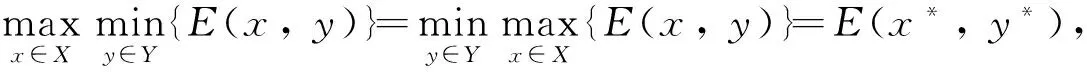
3二人零和语言值矩阵对策的线性规划求解模型

每个局中人都是在对方的每个纯策略下，考虑选择使自己的语言期望支付值达到最大的混合策略. 当局中人P1选用混合策略x∈X、 局中人P2选用纯策略γj∈C2时，局中人P1的语言期望支付值为

其中: A•j是矩阵A的第j列,E(x，j)是语言值. 局中人P2选取纯策略使E(y，j)达到最小，即为

(1)

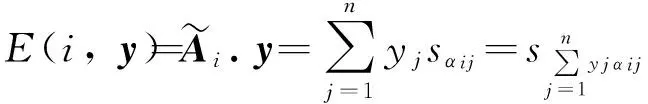
其中： Ai•是矩阵A的第i行，E(i，y)是语言值. 局中人P1选取纯策略使E(i，y)达到最大，即为:

(2)

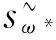
(3)

和

(4)

根据前面的分析，式(3)与 式(4)可以改写成为如下通常的一对对偶线性规划模型：

(5)

和

(6)

4应用实例分析

电商P1和P2争夺某种产品电子商务市场，各自制定策略，以提高自己产品在电子商务市场的销售量. 由于网上消费对这两种产品的需求量是固定的，因此一家电商销售量的提高会引起另一家电商销售量的下降. 两家电商考虑采用下面3种策略来提高自己这两种产品在该市场上的销售量. 策略δ1：网络宣传； 策略δ2：降低价格； 策略δ3：改善物流服务. 两家电商策略的选择问题可以看成一个矩阵对策，即电商P1和P2分别看成两个局中人，均根据语言评估标度集S′={s-3，s-2，s-1，s0，s1，s2，s3}对其局势进行判断、 评估. 电商P1在各局势下的支付矩阵用语言支付矩阵表示如下:

试确定两家公司的极大-极小与极小-极大策略.

根据S′与语言支付矩阵A，可得语言评估标度矩阵为:

由式(5)与式(6)可构建如下一对对偶线性规划模型:

(7)

和

(8)

5结论

本文研究了支付值为语言值的矩阵对策问题，提出这类矩阵对策的定义与解的概念，建立了局中人极大-极小与极小-极大策略问题的线性规划求解方法. 该方法的主要特点是计算简便、 实用性强. 决策者或专家可通过经验或历史数据评估出不同纯策略局势下的语言评估标度，直接用该方法模型快速计算出最优混合策略及语言对策值，为策略制定提供参考. 该方法可应用于带有模糊语言信息的其他竞争性决策与对策问题，是对经典矩阵对策理论与方法的扩展、 创新. 然而，研究中也发现该方法存在不足. 首先该方法要求决策者对局势的语言评估是准确的、 恰当的，否则计算出的结果会有偏差，甚至错误； 另外，该方法建立在均匀语言评估标度的基础上，实际对策局势评估中存在语言标度非均匀等情况. 显然, 此类语言矩阵对策不适用本文提出的方法. 基于其他语言评估标度方法，建立更有效的语言值矩阵对策的求解方法将是今后的研究工作.

参考文献：

[1]CAMPOSL.Fuzzylinearprogrammingmodelstosolvefuzzymatrixgames[J].FuzzySetsandSystems，1989，32(3): 275-289.

[2]BECTORCR，CHANDRAS，VIJAYV.Matrixgameswithfuzzygoalsandfuzzylinearprogrammingduality[J].FuzzyOptimizationandDecisionMaking，2004，3(3): 255-269.

[3]BECTORCR，CHANDRAS，VIJAYV.Dualityinlinearprogrammingwithfuzzyparametersandmatrixgameswithfuzzypayoffs[J].FuzzySetsandSystems，2004，146(2): 253-269.

[4]LIDF.Afuzzymultiobjectiveapproachtosolvefuzzymatrixgames[J].JournalofFuzzyMathematics，1999，7(4):907-912.

[5] 李登峰. 模糊多目标多人决策与对策[M]. 北京: 国防工业出版社，2003.

[6]NISHIZAKII，SAKAWAM.Fuzzyandmultiobjectivegamesforconflictresolution[M].Heidelberg:Physica-Verleg，2001.

[7]ATANASSOVKT.Intuitionisticfuzzysets[J].FuzzySetsandSystems，1986，20(1): 87-96.

[8]ATANASSOVKT.Intuitionisticfuzzysets[M].Heidelberg:Springer-Verlag，1999.

[9]LIDF.Afastapproachtocomputefuzzyvaluesofmatrixgameswithpayoffsoftriangularfuzzynumbers[J].EuropeanJournalofOperationalResearch，2012，223(2): 421-429.

[10]LIDF.Linearprogrammingapproachtosolveinterval-valuedmatrixgames[J].OMEGA:TheInternationalJournalofManagementScience，2011，39(6): 655-666.

[11 ]LIDF.OWA-basednonlinearmathematicalprogrammingapproachtofuzzymulti-attributegroupdecisionmakingwithlinguisticvariables[J].NewMathematicsandNaturalComputation，2010，6(3): 285-300.

[12]LIDF.Multiattributegroupdecisionmakingmethodusingextendedlinguisticvariables[J].InternationalJournalofUncertainty，FuzzinessandKnowledge-BasedSystems，2009，17(6): 793-806.

(责任编辑： 林晓)

Method for solving matrix games with payoffs of linguistic information

YANG Dianqing，LI Dengfeng

(School of Economics and Management，Fuzhou University，Fuzhou，Fujian 350116，China)

Abstract:The definition of linguistic labels and their operational laws as well as comparison laws are introduced. The definition of matrix games with payoffs of linguistic information and the concept of their solutions are given. The max-min and min-max strategies of two players are calculated by solving a pair of auxiliary linear programming models. A numerical example shows that the proposed method is effective and practical. The theory and method of matrix games with payoffs of linguistic information are not only an extension of those of classical matrix games，but also provide a new route for solving other matrix games with fuzzy linguistic information.

Keywords:linguistic information; matrix game; mathematical programming; game theory

DOI:10.7631/issn.1000-2243.2016.03.0301

文章编号：1000-2243(2016)03-0301-05

收稿日期:2014-06-12

通讯作者:李登峰(1965-)，教授，主要从事经济管理决策与对策、 运筹管理等方面研究，lidengfeng@fzu.edu.cn

基金项目：国家自然科学基金资助项目(71231003，71171055)； 福建省社会科学规划资助项目(2012C022，FJ2015C141，FJ2015B185)； 福建省中青年教师教育科研资助项目(JA13392S)； 福州大学社科科研扶持基金资助项目(15SKF13)

中图分类号：O225

文献标识码：A