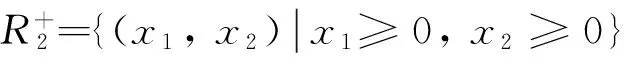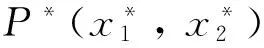具有时滞和避难所的复合型竞争合作模型的Hopf分支

周青娇, 魏凤英

(福州大学数学与计算机科学学院, 福建 福州　350116)

具有时滞和避难所的复合型竞争合作模型的Hopf分支

周青娇, 魏凤英

(福州大学数学与计算机科学学院, 福建 福州350116)

摘要：考虑一类具有时滞及避难所的复合型竞争合作模型的Hopf分支情况, 通过分析雅克比矩阵的特征值证明当时滞τ在一定范围内变化时, 正平衡点是局部渐近稳定的. 当时滞τ穿过某些特定值时, 该模型在正平衡点附近产生Hopf分支. 最后, 通过数值模拟验证所得结论的有效性.

关键词：复合型竞争合作系统; 避难所; 时滞; Hopf分支

0引言

在Lotka-Volterra模型中, 两种群间的作用总是固定不变的： 负相关、 中性或者正相关. 一般认为，当两种群竞争相同的食物来源时，其中一个种群的存在会抑制另一个种群的增长. 在传统的Lotka-Volterra竞争模型中, 我们总是假设两种群间的作用是负相关的. 但在自然环境中，竞争的种群间的作用也可以是正相关的. 例如，豆类植物虽然跟附近的植物是竞争的, 但处于低密度时, 它会为附近的植物提供氮气[1], 此时豆类植物是有利于其它植物的生长[2]. 另外, 有学者研究表明动物间也存在着互利[3]. 目前，已经有许多学者对具有复合作用的物种进行相关研究[3-7]. 其中文[3]在Lotka-Volterra模型的基础上，提出了复合型竞争合作模型. 复合模型指的是, 两种群间的作用并不总是固定的: 当种群的密度小于某个临界值时, 它对另一个种群的作用是合作的； 当种群的密度大于这个临界值时, 它对另一个种群的作用是竞争的. 该模型为:

(1)

其后, 文[4]对如下的模型进行详细的研究:

(2)

其中, x2种群对x1种群始终是竞争的. x1种群对x2种群是复合作用的: 当x1b时, x1种群对x2种群是竞争的．

另一方面，许多学者研究表明人类的活动严重影响生物的生存. 杨道德等[8]认为许多哺乳动物濒危灭绝的部分原因是动物生存环境的破坏. 赵洪峰等[9]指出鸟类濒临灭绝的主要原因是人为干扰所造成的栖息地破坏. 为保护濒危物种, 我国已建立自然保护区为这些物种提供避难所. 目前, 虽有学者研究过竞争模型的Hopf分支[10], 但尚未有学者同时考虑具有避难所和时滞的复合型竞争合作模型的Hopf分支问题.

本研究在模型 (2)的基础上引入避难所．假设x2种群是濒危物种, 人类为x2种群提供避难所. 在避难所的作用下, 可以将x2种群分为两个部分, mx2表示躲进避难所的x2种群的密度, (1-m)x2表示与x1种群发生作用的种群密度, 且0

(3)

1Hopf分支

将系统(3)改写成：

(4)

其中: a11=a1(1-m), a22=a2(1-m).

(5)

(6)

(7)

分离式(7)的实部和虚部, 得到

(8)

由式(8)有

(9)

矛盾. 因此cosωτ=0, 从而sinωτ=1或者-1. 以下分两种情形讨论.

情形1sinωτ=1.

由式(9)得

(10)

(11)

情形2sinωτ=-1.

由式(9)得

(12)

定理1对于系统(3)有:

(i)P0(0, 0), P1(c1, 0)不稳定.

(ii)当c1c2a1(1-m)时, P2(0, c2)是不稳定的.

2数值模拟

(13)

(14)

参考文献：

[1] BERTNESS M D, LEONARD G H. The role of positive interactions in communities: lessons from intertidal habitats[J]. Ecology, 1997, 78(7): 1 976-1 989.

[2] ZHANG B, ZHANG Z, LI Z,etal. Stability analysis of a two-species model with transitions between population interactions[J]. Journal of Theoretical Biology, 2007, 248(1): 145-153.

[3] ZHANG Z. Mutualism or cooperation among competitors promotes coexistence and competitive ability[J]. Ecological Modelling, 2003,164(2): 271-282.

[4] WANG Y, WU H. A mutualism-competition model characterizing competitors with mutualism at low density[J]. Mathematical and Computer Modelling, 2011, 53(9): 1 654-1 663.

[5] RITA H, RANTA E. Competition in a group of equal foragers[J]. The American Naturalist, 1998, 152(1): 71-81.

[6] NEUHAUSER C, FARGIONE J E. A mutualism-parasitism continuum model and its application to plant-mycorrhizae interactions[J]. Ecological Modelling, 2004, 177(3): 337-352.

[7] HERNANDEZ M J. Spatiotemporal dynamics in variable population interactions with density-dependent interaction coefficients[J]. Ecological Modelling, 2008, 214(1): 3-16.

[8] 杨道德, 蒋志刚, 马建章, 等. 洞庭湖流域麋鹿等哺乳动物濒危灭绝原因的分析及其对麋鹿重引入的启示[J]. 生物多样性, 2005, 13(5): 451-461.

[9] 赵洪峰, 高学斌, 雷富民, 等. 中国受胁鸟类的分布与现状分析[J]. 生物多样性, 2005, 13(1): 12-19.

[10] ZHANG J, JIN Z, YAN J,etal. Stability and Hopf bifurcation in a delayed competition system[J]. Nonlinear Analysis: Theory, Methods & Applications, 2009, 70(2): 658-670.

(责任编辑： 林晓)

Hopf bifurcation of a mixed cooperation-competition model incorporating time delay and refuge

ZHOU Qingjiao, WEI Fengying

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou，Fujian 350116, China)

Abstract:The Hopf bifurcation of a mixed cooperation-competition model incorporating time delay and refuge is considered in this paper. By analyzing the eigenvalues of Jacobian matrices, we prove the local asymptotical stability of the positive equilibrium over a range of the delay and when τ passes through some special value, Hopf bifurcations occur at the positive equilibrium of the model. Numerical simulations are carried out to illustrate the effectiveness of our results.

Keywords:mixed cooperation-competition model; refuge; time delay; Hopf bifurcation

DOI:10.7631/issn.1000-2243.2016.03.0320

文章编号：1000-2243(2016)03-0320-05

收稿日期:2014-01-05

通讯作者:魏凤英(1976-)，教授，主要从事随机微分方程与生物数学研究，weifengying@fzu.edu.cn

基金项目：国家自然科学基金资助项目(11201075)； 福建省自然科学基金资助项目(2010J01005)

中图分类号：O175.14

文献标识码：A