局部窗口动态选择的RSF模型

林 静，王美清

(福州大学数学与计算机科学学院，福建 福州　350116)

局部窗口动态选择的RSF模型

林 静，王美清

(福州大学数学与计算机科学学院，福建 福州350116)

摘要：针对PDE(partial differential equation)图像分割模型-RSF(region-scalable fitting energy)模型对初始轮廓线选择敏感问题，提出根据图像的灰度变化信息动态选择高斯核函数窗口大小的改进RSF模型. 实验表明, 该模型提高了RSF模型对初始轮廓线的鲁棒性.

关键词：图像分割； RSF模型； 高斯核函数； 边缘停止函数

0引言

基于PDE(partial differential equation)模型的图像分割方法是当前研究热点之一. 这类方法最早可追溯到1987年Kass等提出的活动轮廓模型，即snake模型[1]. 该模型在轮廓曲线上定义能量泛函，然后把图像分割问题归结为该能量泛函的最小化问题. 由于该模型提取的目标精确且连续光滑，因此引起人们的极大兴趣，提出了各种改进模型，如MS模型[2]、 GAC模型[3]和CV模型[4]，以及用于处理非同质图像的PS模型[5-6]、 RSF模型[7-8]等. 其中RSF模型从局部信息出发构造能量泛函，对如医学图像等非同质图像有较好分割效果，因此得到广泛研究.

由于RSF模型只利用图像的局部信息，因此容易陷入局部最小值，在实际应用中表现为对初始轮廓线和高强度噪声敏感. 针对RSF模型对初始轮廓线敏感问题，文献[9-10]将CV模型和RSF模型的能量泛函进行了加权组合，提出了LGIF(local and global intensity fitting)模型. 该模型结合了CV模型对初始轮廓线位置、 噪声不敏感和RSF模型能够处理非同质图像的优点. 但是权值需人为设定，且不同图像权值差异较大，给使用者带来不便. 文献[11]提出了结合图像局部熵的WRSF(weighted region-scalable fitting)模型，部分改善了RSF模型对初始轮廓线和噪声的敏感性. 文献[12]提出了结合全局和双核(即灰度域上的核函数和RSF模型的空域核)局部拟合的活动轮廓分割模型.

本文主要针对RSF模型对初始轮廓线的敏感性展开研究. 对比CV模型和RSF模型可以发现，CV模型只考虑背景和目标两个区域的平均性质，是一个全局模型，因此对初始轮廓线的位置不敏感，但不能分割局部细节丰富的非同质图像； 而RSF模型则采用每个像素点周围邻域的平均性能，是一个局部模型，虽可分割非同质图像，但对初始轮廓线的位置敏感. 当初始轮廓线选择不好时会陷入极小值而得不到正确解. 当邻域范围扩大至整个图像区域时，RSF模型退化为CV模型. 因此本文提出了根据图像的灰度变化信息动态选择高斯核函数窗口大小的改进RSF模型. 实验表明，改进的RSF模型不仅能保持RSF模型处理非同质图像的能力，而且提高了RSF模型对初始轮廓线的鲁棒性.

1RSF模型分析

1.1RSF模型

李纯明等[8]提出利用图像局部灰度信息分割非同质图像的RSF模型. 设I: Ω⊂R2→R为灰度图像，C是Ω上的封闭曲线，将Ω分割为外部Ω1=outside(C)和内部Ω2=inside(C)两个区域. 对任一给定的像素点x∈Ω，文献[8]首先定义局部灰度拟合(LIF)能量：

(1)

在局部灰度拟合(LIF)能量的基础上，综合考虑轮廓线C的光滑性和演化曲线拓扑变化等性质，RSF模型给出的能量泛函的水平集表示形式为：

(2)

对于固定的水平集函数φ，使F(φ，f1(x)，f2(x))达到最小的f1(x)和f2(x)为：

(3)

1.2RSF模型分析

在式(2)给出的RSF模型中，Kσ是窗口大小为(4σ+1)×(4σ+1)的高斯核函数，因此像素点x在轮廓线外部和内部的拟合值f1(x)、 f2(x)实际是以x为中心的(4σ+1)×(4σ+1)的窗口内所有像素值的加权平均，分析结果如图1所示. 图1(a)为原始图像及初始轮廓线，图1(b)为RSF模型迭代停止时的分割结果. 图上标出了目标边缘上点p1的外部和内部拟合值{f1，f2}，以及与该点相邻的外部点p2和内部点p3的像素值. 在p1处，f1=118.0，近似于该点外部邻域点p2的灰度值； 类似地，f2=67.3，近似于该点内部邻域点p3的灰度值.

(a)原始图像和初始轮廓线

(b)RSF模型迭代停止时的分割结果

(a)二值图像和初始轮廓线

(b)RSF模型迭代停止时的分割结果

为了消除这类伪边缘，文献[11]通过局部熵来调整核函数的权值分布，把能量泛函修改为(水平集表示形式)如下形式：

(4)

2局部窗口动态选择模型

(a)二值图像和初始轮廓线

(b)本文模型迭代停止时的分割结果

相应地，RSF模型(2)修改为：

(5)

采用梯度下降流方法求解能量泛函(5). 对固定的水平集函数φ，使F(φ，f1(x)，f2(x))达到最小的f1(x)和f2(x)为：

(6)

对于固定的f1(x)和f2(x)，使F(φ，f1(x)，f2(x))达到最小的φ应满足：

(7)

其中:δε是Hε的导数.

在数值实现中，采用与文献[8]中对RSF模型类似的实现方式. 式(7)可以通过一个有限差分方案(时间向前-空间中心差分格式)来离散化. 水平集函数初始化为二值函数，即在初始轮廓线内部取负值-c0，外部取正值c0. 在本文实验中选取c0=2.

3实验结果与分析

图4为RSF、 WRSF和本文模型在3个不同大小的初始轮廓位置对X-ray1血管图像的分割效果. 从图中可看出，RSF模式、 WRSF模式对三个初始轮廓位置都不能正确分割； 而本文模型均可得到理想分割效果.

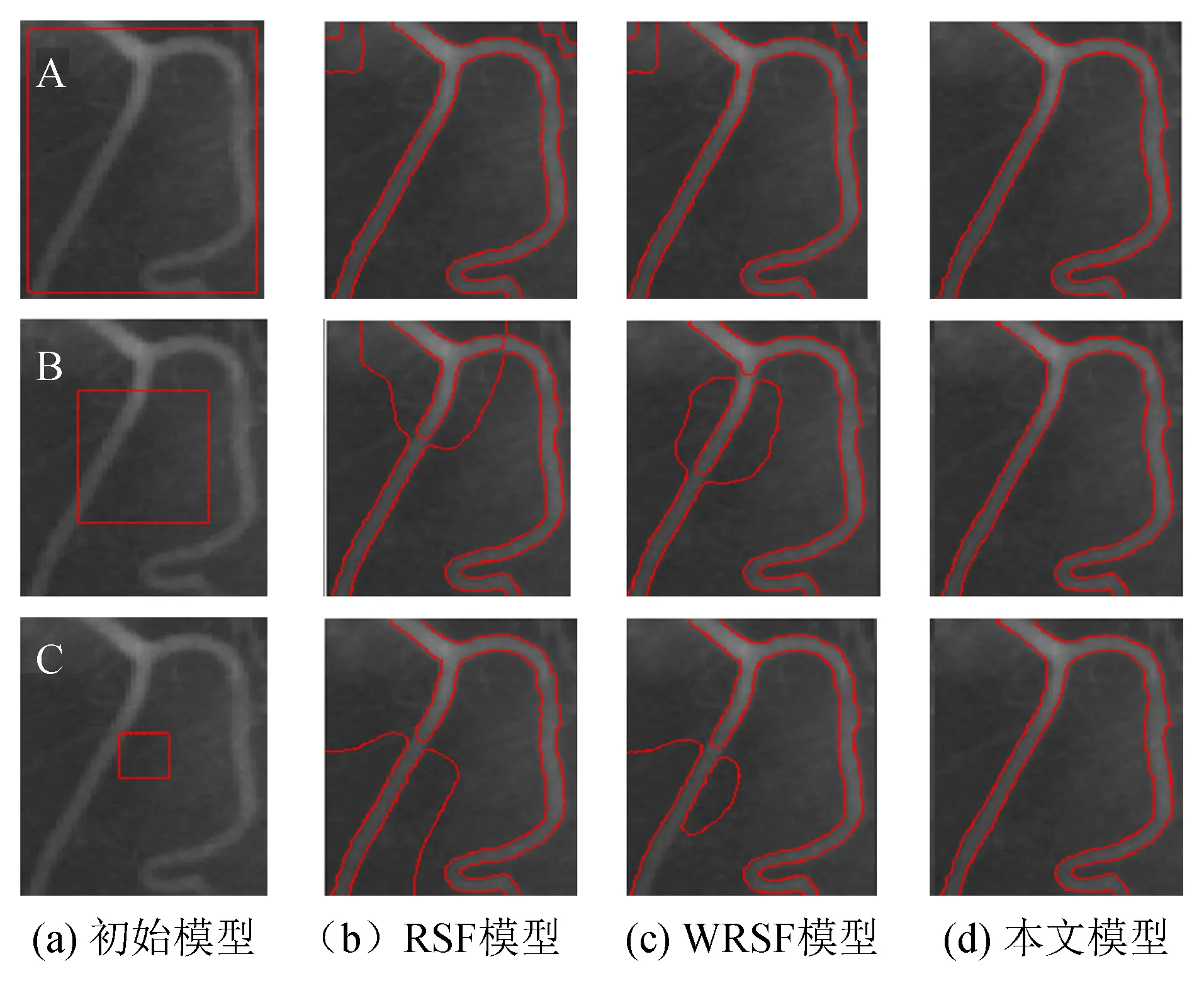
图4　　　　RSF模型、 WRSF模型和本文模型对X-ray1　　　血管图像的分割结果Fig.4　　　　Segmentation results of the RSF model、 WRSF model 　　　and new RSF model for a X-ray1 image

图5　　　　RSF模型、 WRSF模型和本文模型对X-ray2　　　血管图像的分割结果Fig.5　　　　Segmentation results of the RSF model、 WRSF model 　　　 and newRSF model for a X-ray2 image

图5为RSF、 WRSF和本文模型在3个不同大小的初始轮廓位置对X-ray2血管图像的分割效果. 从图中可看出，RSF模式对三个初始轮廓位置都不能正确分割； WRSF模式除对C初始轮廓位置能正确分割外，对A、 B初始轮廓线位置都不能正确分割； 而本文模型均可得到理想分割效果. 其中本文模型中参数ν选0.0025×255×255.

图6为RSF模型、 WRSF模型和本文模型在8个不同初始轮廓位置对人造图像的分割结果. 从图中可看出, RSF模型对8个初始轮廓线位置都不能正确分割； 从WRSF模型除对C初始轮廓位置能正确分割外，对其他初始轮廓线位置都不能正确分割；而本文模型均可得到理想分割效果. 其中本文模型中参数v选0.003×255×255，γ=19.

图6　RSF模型、 WRSF模型和本文模型对人造图像的分割结果Fig.6　Segmentation results of the RSF model、 WRSF model and new RSF model for a synthetic image

4结语

针对RSF模型对初始轮廓线敏感的问题，提出了根据图像的灰度变化信息动态调整高斯核函数窗口大小的改进RSF模型. 在灰度变化缓慢的同质区域，选用较大窗口来计算局部拟合能量； 而在细节丰富的区域，则选用较小窗口. 窗口的动态调整通过边缘检测函数来实现. 实验表明，该模型不但能处理非同质图像的能力，而且提高了RSF模型对初始轮廓线的鲁棒性. 但是，引入窗口较大的高斯核函数使得所提方法的计算量增大，特别是对那些尺寸较大的图像. 因此下一步工作将通过采用不同的优化方案来加快收敛速度.

参考文献：

[1] MICHAEL K, ANDRE W，DEMETRI T. Active contour models[J]. International Journal of Computer Vision，1987，1(4): 321-331.

[2] MUMFORD D，SHAH J. Optimal approximation by piece-wise smooths functions and associated variational problems[J]. Communications on Pure and Applied Mathematics，1989，42(5): 677-685.

[3] CASELLES V, KIMMELS R，SAPIRO G. Geodesic active contours[J]. Comput Vis，1997，22(1): 61-79.

[4] CHAN T，VESE L. Active contours without edges[J]. IEEE Trans Image Process，2001，10(2): 266-277.

[5] TSAI A，YEZZI A，WILLSKY A S. Curve evolution implementation of the Mumford-Shah functional for image segmentation，denoising，interpolation，and magnification[J]. IEEE Transaction on Image Processing，2001，10(8): 1 169-1 186.

[6] VESE L A，CHAN T F. A multiphase level set framework for image segmentation using the Mumford-Shah model[J]. International Journal of Computer Vision，2002，50(3): 271-293.

[7] LI C，KAO C，GORE J，etal. Implicit active contours driven by local binary fitting energy[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Minneapolis: IEEE，2007： 1-7.DOI: 10.1109/CVPR.2007.383014.

[8] LI C，KAO C，GORE J C，etal. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Trans Image Process，2008，17(10): 1 940-1 949.

[9] WANG L，LI C，SUM Q，etal. Brain MR image segmentation using local and global intensity fitting active contours/surfaces[J]. Proceedings of Medical Image Computing and Computer Aided Intervention (MICCAI)，2008，11(1): 384-392.

[10] WANG L，LI C，SUN Q，etal. Active contours driven by local and global intensity fitting energy with application to brain MR image segmentation [J]. Computerized Medical Imaging and Graphics，2009，33(7): 520-531.

[11] HE C J，WANG Y，CHEN Q. Active contours driven by weighted region-scalable fitting energy based on local entropy[J]. Signal Processing，2012，92(2): 587-600.

[12] 赵杰，祁永梅，潘正勇. 结合全局和双核局部拟合的活动轮廓分割模型[J]. 计算机应用，2013，33(4): 1 092-1 095.

(责任编辑： 蒋培玉)

An improved RSF model changing dynamically the size of local windows

LIN Jing，WANG Meiqing

(College of Mathematics and Computer Science，Fuzhou University，Fuzhou，Fujian 350116，China)

Abstract:RSF (region-scalable fitting energy) model is a famous PDE(partial differential equation) image segmentation model，which is sensitive to initialization. To address this problem，a modified RSF model whose the window size of Gaussian kernel function to each pixel in images be selected dynamically is proposed. The window sizes of Gaussian kernel functions of the model depend on the intensity of images. The experimental results show that the proposed model allows for more robustness to initialization compared to the original RSF model.

Keywords:image segmentation； region-scalable fitting energy model； Gaussian kernel function； edge stopping function

DOI:10.7631/issn.1000-2243.2016.03.0413

文章编号：1000-2243(2016)03-0413-06

收稿日期:2013-08-16

通讯作者:王美清(1967-), 教授、 博士生导师, 主要从事图像处理技术、 数值计算技术等方面研究，mqwang@fzu.edu.cn

基金项目:国家自然科学基金资助项目(11071270)

中图分类号：TP391

文献标识码：A