不同轴压比下叠合板式剪力墙结构抗震性能分析

杨联萍, 余少乐, 张其林, 崔家春

(1．同济大学 土木工程学院，上海　200092； 2．上海现代建筑设计(集团) 有限公司，上海　200041 )

不同轴压比下叠合板式剪力墙结构抗震性能分析

杨联萍1,2, 余少乐1, 张其林1, 崔家春2

(1．同济大学 土木工程学院，上海200092； 2．上海现代建筑设计(集团) 有限公司，上海200041 )

摘要：叠合板式剪力墙结构是一种新型的装配式结构，它吸收了现浇混凝土结构与预制混凝土结构的优点，已经在国内中低层建筑中推广应用。目前的研究只是针对低轴压比下的抗震性能，将其推广应用于高层建筑中必然要开展高轴压比下抗震性能的研究。首先从理论上推导了在高轴压比下叠合板式剪力墙的极限承载力，结果表明叠合板式剪力墙由于预制层中混凝土强度等级高于现浇层的混凝土，在高轴压比下叠合剪力墙的极限承载力达到甚至超过了现浇整体剪力墙。基于OpenSEES采用两种不同模型对叠合板式剪力墙在不同轴压比下的受力性能进行模拟。第一种是多垂直杆单元模型，第二种是模型是纤维截面模型。模拟结果验证了理论推导的正确性，边缘构件预制的叠合剪力墙的极限承载力在高轴压比下要高于边缘构件现浇的叠合剪力墙，而且边缘构件预制的叠合剪力墙施工更加方便。因此预制边缘构件的叠合剪力墙推广价值更大。

关键词：建筑工业化; 叠合板式剪力墙;多垂直杆单元模型；纤维截面模型；轴压比

绿色建筑是目前建筑行业的发展方向，装配式建筑响应绿色施工的政策要求，应用日益广泛。叠合剪力墙结构是装配式结构的一种，不仅具有装配式结构工厂化生产、现场施工方便的优点，还兼备了现浇混凝土的整体性，是一种新型的绿色结构体系。目前叠合剪力墙结构已经在我国推广开来，但是多应用于低烈度地震区中的中低层结构体系，将其应用于高烈度地震区还受到了很大的限制[1]。目前开展的针对于叠合剪力墙结构的研究还只局限于低轴压比下的叠合剪力墙构件的抗震性能，因此要将叠合剪力墙推广应用于高层建筑中，要对其在高轴压比下的抗震性能进行进一步的分析。本文针对目前常用的两种形式的叠合剪力墙(边缘构件现浇的叠合剪力墙和边缘构件预制的叠合剪力墙)展开讨论，研究其在不同轴压比下的抗震性能，并与现浇剪力墙作对比，讨论在不同轴压比下叠合剪力墙和现浇剪力墙的区别。

1叠合板式剪力墙的构造及研究现状

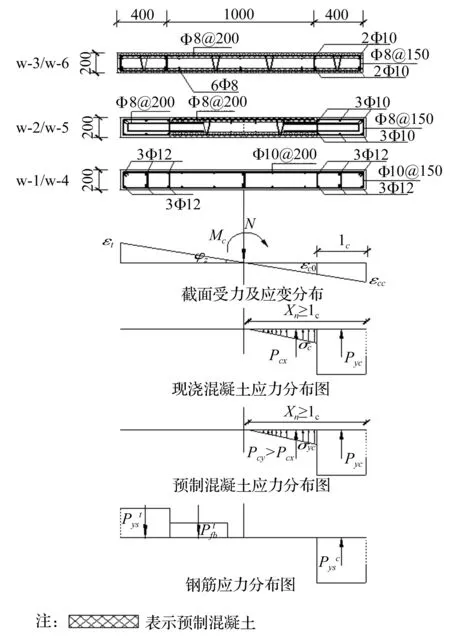
叠合板式剪力墙是由两层混凝土预制板通过格构钢筋的连接，经工厂化制作而成的半预制混凝土墙板，用斜支撑作为叠合式墙板的临时支撑，调节其垂直度、保证叠合式墙板的稳定性，并能够承受风荷载及新浇注混凝土的侧压力，用塑料垫片控制叠合板式剪力墙安装时下部水平标高，以保证墙板顶部的水平标高及其下部留有40 mm 左右的空隙，基本构造如图1所示。

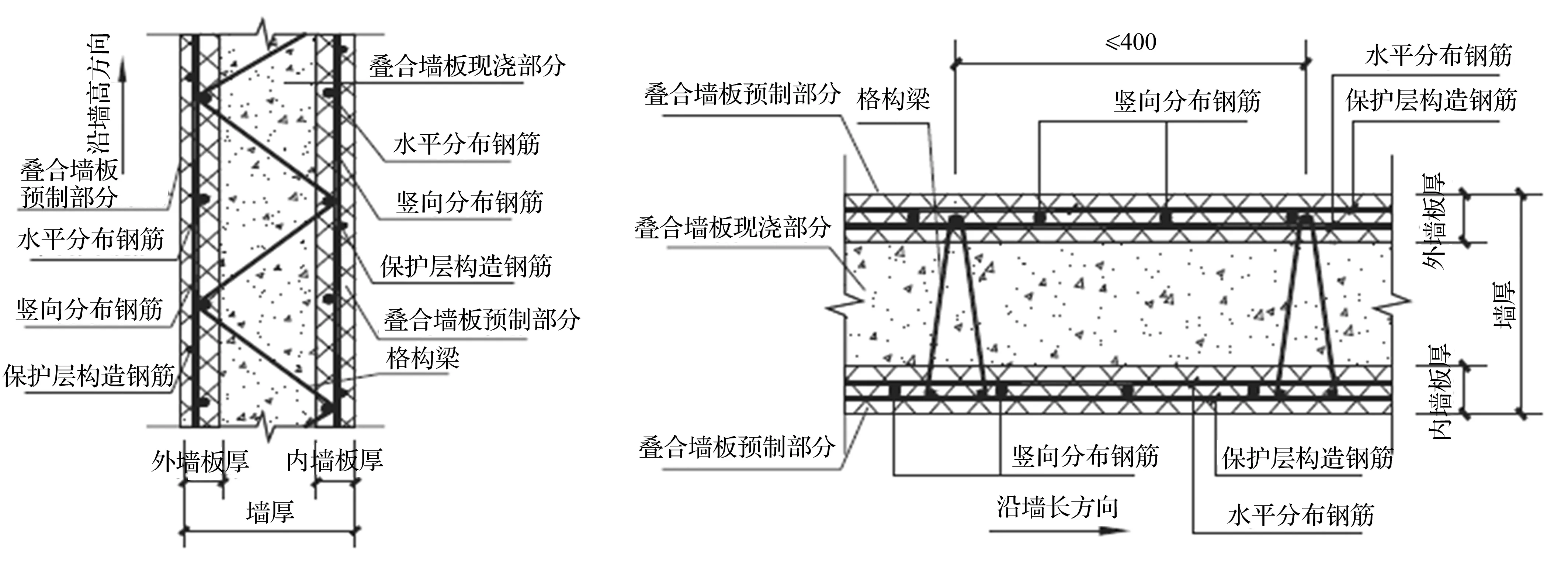
图1　叠合板式剪力墙基本构造Fig.1 Structural details of superimposed shear wall

连星等[2 -6]针对叠合剪力墙在低轴压比下的抗震性能开展了一系列的研究，研究结果表明：在低轴压比(0.1轴压比)下预制叠合板式剪力墙的受力变形过程、破坏形态与现浇剪力墙类似，叠合板式剪力墙的极限承载能力、变形能力和延性低于普通钢筋混凝土剪力墙。两种不同叠合剪力墙(边缘构件现浇的叠合剪力墙和边缘构件预制的叠合剪力墙)在低轴压比下的抗震性能基本相同。王滋军等[7 -9]对添加保温层的叠合剪力墙和现浇自密实混凝土叠合剪力墙进行低轴压比(0.1/0.2轴压比)下的抗震研究，研究表明：叠合剪力墙的承载能力、变形能力和现浇剪力墙和几乎相同，保温层外侧的预制部分能够参与工作，提高了叠合剪力墙的极限承载力。Benayoune等[10]研究了预制叠合板墙体在轴心荷载作用下的性能，研究表明:在轴心荷载作用下，所有的叠合板墙体均作为一个整体进行工作，直至破坏。

2叠合板式剪力墙极限承载力理论分析

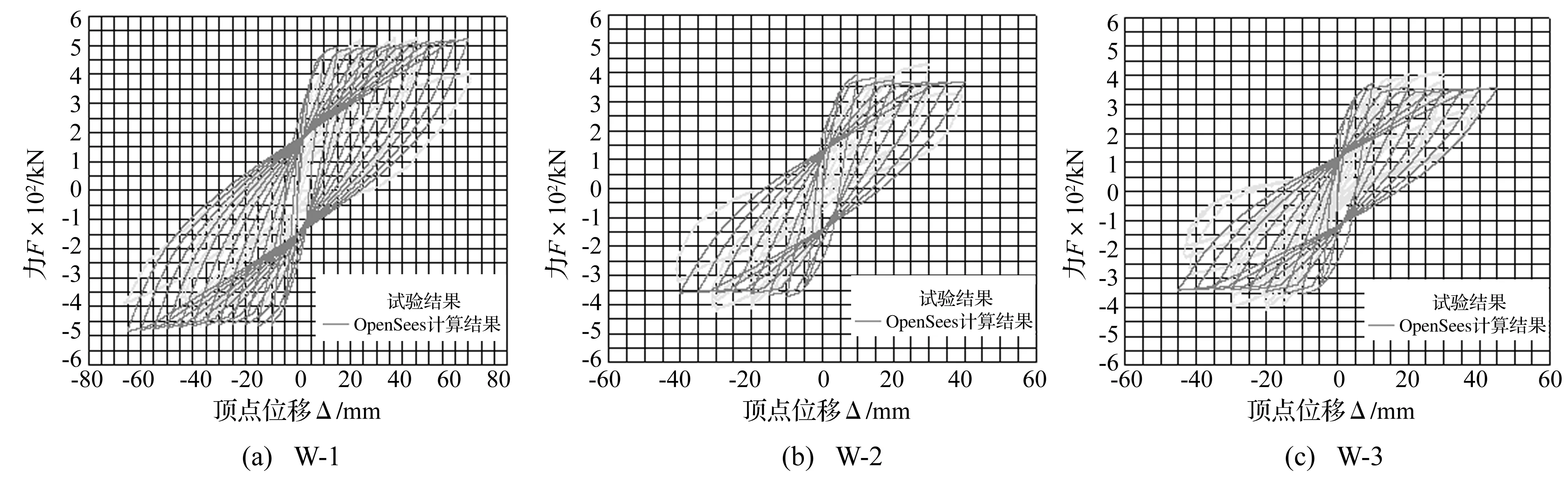
选用文献[2]中的试验构件进行理论分析，并与试验结果进行对比。本文对W-1/w-4(现浇剪力墙)以及不同边缘构件形式的叠合板式剪力墙W-2/w-5(边缘构件现浇)和W-3/w-6(边缘构件预制)进行理论分析，揭示预制层在整个受力过程中不同阶段参与工作的程度，试件具体参数见文献[2]。试验结果表明叠合面之间的没有产生黏结滑移，因此在推导叠合板式剪力墙极限承载力时不考虑叠合面之间的滑移。极限承载力状态时混凝土截面应力-应变如下图2所示(考虑大偏心受压的情况)。

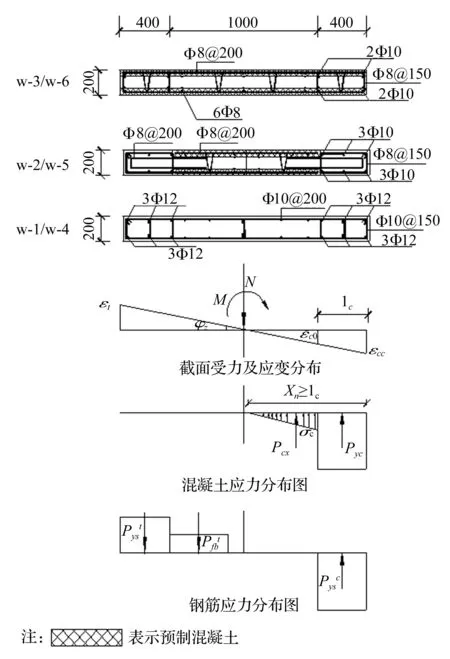
图2　极限状态下截面应力-应变图Fig.2 The stress-strain distribution of section under limit state

对于极限状态，当受压区高度xn≥lc时，此时墙体两端主受力筋均屈服，认为距离受压区外边缘1.5xn以外部分的竖向分布钢筋均屈服，截面的纵向压力为N,根据竖向力的平衡关系得:

(1)

(2)

将相关参数代入式(2)中，可以求得

(3)

对截面的形心轴取矩，剪力墙截面的峰值受弯承载力为：

Mp=fccbw(hw-lc)/2+

ffbρv(hw-1.5xn)bw(1.5xn-lc)/2

(4)

当受压区高度xn

(5)

将相关参数代入式(3)中，可以求得：

xn=

N+ffbbwρvhw+fyAs-EsεcuAs)/2×(1.5ffbbwρv-bwfcc)

(6)

对截面的形心轴取矩，剪力墙截面的受弯承载力为：

Mp=fccbwxn(hw-xn)/2+fyAs(hw/2-as)+σyAs(hw/2-

as′)+ffbρv(hw-1.5xn)bw(1.5xn-lc)/2

(7)

峰值荷载为：

Fp=Mp/H

(8)

2.1理论公式的验证

2.1.1W-1构件

在考虑叠合构件整体工作前，用理论推导文献[2]中现浇整体构件W-1的理论解，和试验对比论证理论解的合理性。

当xn≥lc时，现浇墙体受压区高度按照式(3)可得：xn=-81.52 mm。可见，受压区高度xn

2.1.2W-2构件

达到极限状态时边缘构件达到受压极限状态，由于预制层混凝土强度高，现浇层强度低，现浇层到达极限受压状态时，预制层达不到极限状态，因此预制层混凝土强度取强度较低现浇层强度。

当xn≥lc时，叠合剪力墙体受压区高度按照式(3)可得：xn=-148.504 mm。可见，受压区高度xn

2.1.3W-3构件

当叠合面之间无滑移时，预制层和现浇层形成整体共同工作。达到极限状态时边缘构件达到受压极限状态，由于预制层混凝土强度高，现浇层强度低，现浇层到达极限受压状态时，预制层达不到极限状态，因此预制层混凝土强度取强度较低现浇层强度。桁架钢筋是由三根纵筋和斜向腹筋组成，三根纵筋的作用和普通的纵向钢筋一样，同样参与受力。W-3构件的暗柱区内存在桁架钢筋，因此分两种情况推导极限承载力。

(1) 当不考虑约束区的桁架钢筋的作用

当xn≥lc时，叠合剪力墙体受压区高度按照式(3)可得：xn=-550.62 mm。可见，受压区高度xn

(2) 考虑约束区的桁架钢筋的作用

桁架钢筋面积较小，对受压区高度的变化影响不大，因此只考虑受压区高度xn

从前面的分析可以看出，对叠合板式剪力墙的理论计算结果和试验值较为接近，进一步证明叠合面之间没有滑移。W-3构件考虑约束区桁架钢筋作用时的结果比不考虑约束区桁架钢筋作用时的结果更加接近试验值，证明约束区的桁架钢筋在叠合剪力墙中不仅起连接作用，也参与受力。

表1　极限承载力理论计算和试验值对比

利用上面计算的公式分别推导0.2、0.3、0.4、0.5轴压比下现浇剪力墙和叠合剪力墙的极限承载力，计算结果统计如表2所示。

表2　不同轴压比下极限承载力对比

2.2高轴压比下理论公式的改进

从上表可以看出当轴压比≥0.3时，受压区高度xn>lc。在推导极限承载力时并没有考虑叠合板剪力墙中预制层混凝土强度的提高，显然与实际有所差别。叠合剪力墙受压截面的应变虽然呈线性分布，但是预制层和现浇层混凝土强度却不同，其受力见图3。

假定预制层边缘处混凝土压应力达到σyc=η1σc，受压部分混凝土根据力的平衡把预制层等换成现浇层有如下关系：

(9)

可见受压部分的混凝土强度提高系数为

(10)

对截面的形心轴取矩，剪力墙截面的极限受弯承载力为：

Mp=ξcfccbwlc(hw-lc)/2+

ffbρv(hw-1.5xn)bw(1.5xn-lc)/2

(11)

极限承载力为：

Fp=Mp/H

(12)

根据预制层强度和现浇层强度等级，取η1=1.4，因此受压部分提高系数可取为1.2。考虑混凝土预制层强度的提高，推导0.1、0.2、0.3、0.4、0.5轴压比下现浇剪力墙和叠合剪力墙的极限承载力，计算结果统计如表3所示。

将上面的分析结果绘制成图4，分析表明：随着轴压比的增大，现浇剪力墙和预制剪力墙的极限承载力均逐渐增大。不考虑预制层混凝土强度等级高于现浇层混凝土强度的因素，分析结果表明现浇剪力墙的极限承载力>边缘构件现浇的叠合剪力墙>边缘构件预制的叠合剪力墙。考虑预制层混凝土强度等级高于现浇层混凝土强度的因素，分析结果表明轴压比大于0.3(含0.3)时，边缘构件预制的叠合剪力墙的极限承载力超过边缘构件现浇的叠合剪力墙；轴压比大于0.4时边缘构件预制的叠合剪力墙极限承载力>现浇剪力墙的极限承载力>边缘构件现浇的叠合剪力墙。

表3　不同轴压比下极限承载力对比(考虑预制层强度等级的提高)

图3　叠合墙中含预制部分截面应力-应变图Fig.3 The stress-strain distribution of section of prefabricated parts under limit state

图4　不同轴压比下三个不同构件极限承载力对比Fig.4 The comparison of ultimate bearing capacity under different axial-load ratios

叠合剪力墙中预制层混凝土强度等级高于现浇剪力墙，其作用不能忽视。预制边缘构件的叠合剪力墙在现场施工中较现浇边缘构件的叠合剪力墙更为方便，当考虑预制层中混凝土强度等级高于现浇层混凝土强度这个有利因素时，预制边缘构件的叠合剪力墙的极限承载力在高轴压比下高于边缘构件现浇的叠合剪力墙和整体现浇剪力墙。为了对此观点进行验证，下面通过有限元分析，继续论证不同轴压比下叠合剪力墙和现浇剪力墙的区别。

3基于OpenSEES的叠合板式剪力墙非线性有限元分析

选用文献[2]中的W-1，W-2，W-3(0.1轴压比)；W-4，W-5，W-6(0轴压比)试件，进行有限元分析。利用开源程序OpenSEES(Open System for Earthquake Engineering Simulation)，采用两种不同模型对叠合板式剪力墙进行模拟。第一种是多垂直杆元模型，第二种是纤维截面模型(构件的详细参数见文献[2])，首先通过0/0.1轴压比下的试验和有限元模型对比，验证模型的正确性，进而分析0.2、0.3、0.4、0.5轴压比下现浇剪力墙和叠合板式剪力墙低周反复荷载作用下的滞回特性的区别。

3.1多垂直杆元模型

Kabeyasawa提出了一个宏观的三垂直杆元模型，这一模型可以模拟进入非线性后剪力墙中性轴的移动，但是弯曲弹簧的刚度取值存在一定的困难，弯曲弹簧变形与边柱变形协调困难。为了解决垂直杆元中的问题，Vulano等[11]提出了多垂直弹簧模型，用几个垂直杆件来代替弯曲弹簧，剪力墙的弯曲刚度和轴向刚度由这些弹簧代表，而剪切刚度由一个水平弹簧代表，如图5所示。多垂直杆元模型可以考虑中性轴的移动，也可以把不同材料的恢复力模型综合一起考虑，还可以考虑轴向荷载的变化对强度和刚度的影响。

图5　多垂直杆元模型Fig.5 Multiple vertical line element model

3.1.1单元模型

采用Truss单元模拟竖向弹簧，赋予其纤维截面属性。zerolength单元材料模型剪切弹簧，剪切性能采用Hirosawa利用大量的剪力墙试验建立的经验公式[12]，用OpenSEES中的Hysteretic材料来定义，如图6所示。

图6　Hysteretic材料本构关系Fig.6 Constitutive model of Hysteretic material

3.1.2材料模型

Orakcal等创建了concrete06本构模拟混凝土，concrete06本构通过引入受压软化参数和受拉硬化参数，可以考虑混凝土双轴受压软化和受拉硬化效应。Concrete06本构如图7所示，受压骨架曲线采用的是Thorenfeldt-based曲线。钢筋通过Steel02本构来模拟，Steel02本构是基于Giuffre-Menegotto-Pinto的修正模型，如图8所示，能够考虑钢筋等向应变硬化影响，还可以很好的反映包兴格效。

图7　Concrete06本构Fig.7 Constitutive model of Concrete06

图8　Steel02本构模型Fig.8 Constitutive model of Steel02

3.1.3分析结果

沿着剪力墙高度分成5个单元，每一个单元使用多垂直杆元模型模拟。分析过程分为两步，第一步添加竖向压力，分成十个荷载步完成。第二步施加往复的水平荷载。对六片个剪力墙的模拟结果如图9、10所示。

图9　0.1轴压比下荷载-位移曲线Fig.9 Load-deformation curve under 0.1 axial compression ratio

图10　0轴压比下荷载-位移曲线Fig.10 Load-deformation curve under 0 axial compression ratio

从上面的分析结果可以看出，多垂直杆元模型在低轴压比预测现浇剪力墙和叠合剪力墙的极限承载力上可以达到很好的效果。W-1(现浇构件)的极限承载力为518 kN，OpenSEES模拟结果为524.56 kN，二者相差1.3%；W-2(叠合构件)的极限承载力为429 kN，OpenSEES模拟结果为393.48 kN，二者相差8.3%；W-3(叠合构件)的极限承载力为412 kN，OpenSEES模拟结果为373.389 kN，二者相差9.4%；W-4(现浇构件)的极限承载力为269 kN，OpenSEES模拟结果为310.033 kN，二者相差15.3%；W-5(叠合构件)的极限承载力为240 kN，OpenSEES模拟结果为210.026 kN，二者相差12.5%；W-6(叠合构件)的极限承载力为239 kN，OpenSEES模拟结果为201.512 kN，二者相差15.7%；模拟结果表明，多垂直杆元模型在0/0.1轴压比下模拟现浇剪力墙和叠合剪力墙的极限承载力和试验误差在15%以内，证明模型能够准确的预测现浇剪力墙和叠合剪力墙的极限承载力。接下来对轴压比0.2、0.3、0.4、0.5下三个剪力墙进行模拟，模拟结果如图11～14所示。

图11　0.2轴压比荷载-位移曲线Fig.11 Load-deformation curve under 0.2 axial compression ratio

图12　0.3轴压比荷载-位移曲线Fig.12 Load-deformation curve under 0.3 axial compression ratio

图13　0.4轴压比荷载-位移曲线Fig.13 Load-deformation curve under 0.4 axial compression ratio

图14　0.5轴压比荷载-位移曲线Fig.14 Load-deformation curve under 0.5 axial compression ratio

多垂直杆元模型模拟结果表明：随着轴压比的增加，现浇剪力墙和叠合剪力墙的极限承载力变化趋势是一样的，都是逐渐增大。轴压比0.3以下时，现浇剪力墙滞回曲线较叠合剪力墙滞回曲线饱满些，当轴压比超过0.3以后叠合剪力墙和现浇剪力墙的极限承载力差别越来越小，二者的滞回曲线形状也差别不大。边缘构件预制的叠合剪力墙在轴压比0.5时的极限承载力甚至超过了现浇剪力墙。从上面的分析结果可以看出，在低轴压比下(0、0.1、0.2)现浇剪力墙的滞回性能要优于叠合剪力墙，在高轴压比下(0.3、0.4、0.5)现浇剪力墙的滞回性能和叠合剪力墙的滞回性能差别不大。对比三种剪力墙在不同轴压比下的骨架曲线，可以看出叠合剪力墙和现浇剪力墙的骨架曲线基本相同，图15所示。

图15　三个构件在不同轴压比下骨架曲线对比图Fig.15 The comparison of skeleton curves under different axial-load ratios

将多垂直杆元模型模拟不同轴压比下三种剪力墙的极限承载力与第二部分中理论分析值对比如下图16所示，有限元分析的结果和考虑叠合剪力墙中预制层强度等级不同时的理论值更加接近。其原因是受压区预制层混凝土强度等级较现浇剪力墙强度高，因此在高轴压比下叠合剪力墙的极限承载力超过了现浇剪力墙，验证了文章中第二部分中的结论：在高轴压比下应该考虑叠合墙预制层中混凝土强度等级高的因素对极限承载力的有利影响，边缘构件预制的叠合剪力墙比边缘构件现浇的叠合剪力墙更有推广价值。

图16　不同轴压比下三个不同构件极限承载力对比Fig.16 The comparison of ultimate bearing capacity under different axial-load ratios

3.2纤维截面模型

OpenSEES中纤维截面模型，最早是由Taucer et al.开发了，是目前模拟框架结构和剪力墙结构静力和动力性能使用最为广泛的方法之一。在这个模型中，沿着截面分成很多混凝土纤维和钢筋纤维，分别赋予钢筋纤维和混凝土纤维各自的单轴本构，如图17所示。

图17　纤维截面模型Fig.17 The section fiber model

图18　Concrete01 本构模型Fig.18 Constitutive model of Concrete01

3.2.1单元模型

纤维截面模型中有基于刚度的纤维模型和基于柔度的纤维模型，基于刚度的纤维模型把单元划分为若干个积分区段，积分点处截面的位移通过3次Hermit多项式差值求得，在线性和近似线性的响应下可以得到较为准确的结果，局限于3次差值函数，在不能很好的描叙非线性行为，要到达需要的效果，需要在非弹性区域使用非常细的划分；基于柔度的纤维模型，同样把单元划分为若干个区段，积分点处的截面力通过线性插值求得，在模拟弯曲型梁柱构件时，可以达到很好的收敛效果，在混凝土构件非线性分析时能到取得理想的效果。

3.2.2材料模型

Concrete01本构如上图18所示，其受压骨架曲线采用的是修正的Kent-Park模型，没有考虑混凝土的受拉力学性能。受压骨架曲线分为三段：上升段、下降段和平台段。钢筋通过Steel02本构来模拟，如上图8所示。

3.2.3剪切变形

由于纤维单元无法指定抗剪刚度，因此无法考虑剪力的影响。为了考虑剪力墙的剪切性能，在OpenSEES中通过截面组装(Section Aggregator)，将定义的抗剪本构与纤维截面进行组装以考虑剪切变形的影响。为了考虑剪切滞回性能，剪力墙的剪切本构选用Hirosawa经验公式，使用Hysteretic材料来描述，Hysteretic材料本构如上图6所示。

3.2.4分析结果

沿着剪力墙高度分成10个单元，分析过程分为两步，第一步添加竖向压力，分成十个荷载步完成。第二步施加往复水平位移，位移增量为0.01 mm。对六个剪力墙在0/0.1轴压比下的模拟结果和试验对比如下图19、20所示。

图19　0.1轴压比下荷载-位移曲线Fig.19 Load-deformation curve under 0.1 axial compression ratio

图20　0轴压比下荷载-位移曲线Fig.20 Load-deformation curve under 0 axial compression ratio

从上面的分析可以看出，基于柔度法的纤维单元在0.1轴压比下模拟现浇剪力墙和叠合剪力墙在低周反复荷载作用下的强度降低，刚度退化和捏拢效应，均能够取得较好的效果。W-1(现浇构件)的极限承载力为518 kN，OpenSEES模拟结果为478.564 kN，二者相差3.9%；W-2(叠合构件)的极限承载力429 kN，OpenSEES模拟结果为406.957 kN，二者相差4.6%；W-3(叠合构件)的极限承载力412 kN，OpenSEES模拟结果为371.808 kN，二者相差8.6%；W-4(现浇构件)的极限承载力为269 kN，OpenSEES模拟结果为309.114 kN，二者相差14.9%；W-5(叠合构件)的极限承载力240 kN，OpenSEES模拟结果为226.285 kN，二者相差5.7%；W-6(叠合构件)的极限承载力239 kN，OpenSEES模拟结果为203.53 kN，二者相差14.8%；纤维截面模型在0/0.1轴压比下模拟现浇剪力墙和叠合剪力墙的极限承载力和试验误差在15%以内，证明模型能够准确的模拟现浇剪力墙和叠合剪力墙的滞回特性。接下来对轴压比0.2、0.3、0.4、0.5时三个剪力墙进行模拟，模拟结果如图21～24所示。

从上面的分析结果可以看出，轴压比0.3以下时，现浇剪力墙滞回曲线较叠合剪力墙滞回曲线饱满些，当轴压比超过0.3以后叠合剪力墙和现浇剪力墙的极限承载力差别越来越小，二者的滞回曲线形状也差别不大。在低轴压比下(0、0.1、0.2)现浇剪力墙的滞回性能要优于叠合剪力墙，在高轴压比下(0.3、0.4、0.5)现浇剪力墙的滞回性能和叠合剪力墙的滞回性能差别不大。对比三种剪力墙在不同轴压比下的骨架曲线，可以看出叠合剪力墙和现浇剪力墙的骨架曲线基本相同，如图25所示。

图21　0.2轴压比下荷载-位移曲线Fig.21 Load-deformation curve under 0.2 axial compression ratio

图22　0.3轴压比下荷载-位移曲线Fig.22 Load-deformation curve under 0.3 axial compression ratio

图23　0.4轴压比下荷载-位移曲线Fig.23 Load-deformation curve under 0.4 axial compression ratio

将纤维模型模拟不同轴压比下三种剪力墙的极限承载力与第二部分中理论分析值对比如下图26所示。纤维模型的分析结果也显示当轴压比超过0.4时，叠合剪力墙的极限承载力要高于现浇剪力墙。证明了预制层中混凝土强度等级高在高轴压比下较现浇剪力墙更有优势，边缘构件预制的叠合剪力墙较边缘构件现浇的叠合剪力墙施工中操作方便，更有推广价值。

4结论

(1) 收集的试验结果和有限元模拟结果均表明：叠合面之间在构件破坏之前不会产生黏结滑移，在有限元分析时可以不考虑叠合面之间的滑移问题。

图24　0.5轴压比下荷载-位移曲线Fig.24 Load-deformation curve under 0.5 axial compression ratio

图26　不同轴压比下三个不同构件极限承载力对比Fig.26 The comparison of ultimate bearing capacity under different axial-load ratios

(2) 对叠合板式剪力墙的极限承载力进行理论推导，结果表明随着轴压比增大，现浇剪力墙和预制剪力墙的极限承载力均逐渐增大。理论分析表明当轴压比大于0.3(含0.3)时，由于预制层的混凝土强度等级高于现浇层的混凝土强度等级，边缘构件预制的叠合剪力墙的极限承载力超过边缘构件现浇的叠合剪力墙；轴压比大于0.4时，边缘构件预制的叠合剪力墙极限承载力>现浇剪力墙的极限承载力>边缘构件现浇的叠合剪力墙。叠合板式剪力墙在高轴压比下的极限承载力应考虑预制层混凝土强度等级高的因素带来的影响，提出了计算高轴压比下叠合剪力墙的极限承载力公式。

(3) 基于OpenSEES，通过两种有限元模型(多垂直杆元模型和基于柔度法的纤维单元模型)模拟低轴压比下的结果和试验对比，验证了模型的正确性。在低轴压比下，基于柔度法的纤维单元模型模拟现浇剪力墙和叠合剪力墙在低周反复荷载作用下的强度降低，刚度退化和捏拢效应，均能够取得较好的效果。在预测剪力墙极限承载力上，二者均能达到较高的精度，为以后模拟叠合剪力墙提供了参考。

(4) 在验证模型正确的基础上，利用多垂直杆单元模型和基于柔度法的纤维单元模型模拟得到不同轴压比下叠合剪力墙和现浇剪力墙的滞回曲线，模拟的结果均表明在低轴压比下(0、0.1、0.2)现浇剪力墙的滞回性能要优于叠合剪力墙，在高轴压比下(0.3、0.4、0.5)现浇剪力墙的滞回性能和叠合剪力墙的滞回性能差别不大，对比三种剪力墙在不同轴压比下的骨架曲线，可以看出叠合剪力墙和现浇剪力墙的骨架曲线基本相同。两种不同模型的模拟结果均表明当轴压比大于0.4时，边缘构件预制的叠合剪力墙极限承载力将超过现浇剪力墙的极限承载力，在高轴压比下应该考虑预制层混凝土强度等级高的因素带来的影响，这也与理论分析相符。

(5) 两种不同形式的叠合剪力墙的滞回曲线差别不大，随着轴压比的增大，边缘构件预制的叠合剪力墙的极限承载力超过了边缘构件现浇的叠合剪力墙，甚至超过了现浇整体剪力墙。由于边缘构件预制的叠合剪力墙不仅能够在工厂流水线生产而且施工现场操作更加方便，无需工人现场绑扎预制边缘构件，因此可推广边缘构件预制的叠合剪力墙。

参 考 文 献

[1] Bachmann H，Steinle A. Precast concrete structures[M].Berlin:Wiley-VCH，2011.

[2] 连星.叠合板式剪力墙的抗震性能实验分析及理论研究[D]．合肥：合肥工业大学，2009.

[3] 沈小璞，马巍,陈信堂，等.叠合混凝土墙板竖向拼缝连接抗震性能试验研究[J]．合肥工业大学学报,2010，33(9):1366-1371.

SHEN Xiao-pu,MA Wei,CHEN Xin-tang,et,al. Experimental study of the seismic performance of the vertical joint seam of superimposed concrete wall panels[J]．Journal of Hefei University of Technology，2010，33(9):1366-1371.

[4] 张伟林，沈小璞，吴志新，等．叠合板式剪力墙T 型，L 型墙体抗震性能试验研究[J]．工程力学，2012，29(6):196-201.

ZHANG Wei-lin,SHEN Xiao-pu,WU Zhi-xin,et al. Experimental study of seismic performance on T and L Types Superimposed-shear-walls structure[J]． Engineering Mechanics，2012，29(6)： 196-201.

[5] 李宁《半装配叠合板式剪力墙工字形试件试验研究及数值模拟》[D]．合肥：合肥工业大学，2012.4

[6] 周博文.嵌入式基础叠合板剪力墙平面外受弯性能试验研究与数值模拟分析[D]．合肥：合肥工业大学，2013.4

[7] 王滋军，刘伟庆，叶燕华，等．钢筋混凝土开洞叠合剪力墙抗震性能试验研究[J]．建筑结构学报，2012，33(7):156-163.

WANG Zi-jun,LIU Wei-qing,YE Yan-hua,et al. Experimental study on seismic behavior of reinforced concrete composite shear wall with opening[J]．Journal of Building Structures,2012，33(7):156-163.

[8] 王滋军，刘伟庆，魏威，等．钢筋混凝土水平拼接叠合剪力墙抗震性能试验研究[J]．建筑结构学报，2012，33 (7):147-155.

WANG Zi-jun,LIU Wei-qing,WEI Wei,et al. Experimental study on seismic behavior of reinforced concrete composite shear wall with level splice[J]．Journal of Building Structures,2012，33 (7):147-155.

[9] 叶燕华，孙锐,薛洲海，等.预制墙板内现浇自密实混凝土叠合剪力墙抗震性能试验研究[J]．建筑结构学报，2014，35(7)138-144.

YE Yan-hua,SUN Rui,XEU Zhong-hai,et al.Eperimental study on seismic behavior of SCC and precast NC composite shear wall[J]．Journal of Building Structures,2014,35(7):138-144.

[10] Bcnayounc A，Samad A A A. Structural behaviour of eccentrically loaded precast sandwich panels[J]. Construction and Building Materials,2006,20(9):713-724.

[11] Vulcano A,Bertero V V, ColottiV. Analytical modeling of RC structural walls[J].Proceedings,9th World Conference on Earthquake Engineering,V. 6,Tokyo-Kyoto,Japan,1988:41-46.

[12] Alfonso V，Vitelmo V B.Analytical models for predicting the lateral response of RC shear walls evaluation of their reliability[R].Report No.UCB/EERC-87/19.

Aseismic behavior of superimposed shear walls under different axial load ratios

YANG Lian-ping1,2, YU Shao-le1, ZHANG Qi-lin1, CUI Jia-chun2

(1． College of Civil Engineering，Tongji University，Shanghai 200092，China;2． Shanghai Xiandai Architectural Design (Group) Co．，Ltd，Shanghai 200041，China)

Abstract:The superimposed shear wall is a new assembly-type RC structure, it imbibes advantages of cast-in-place concrete structures and precast concrete structures, now superimposed shear walls are applied in medium-rise and low-rise buildings of seismic zones of China. With increase in the speed of urbanization, more and more high-rise buildings are built, the aseismic behavior of superimposed shear walls with higher axial compression ratios should be investigated so that its application can be extended to high-rise buildings. Here, the theoretical calculation formulas for the ultimate load-bearing capacity of a superimposed shear wall were deduced under higher axial load ratios, the results showed that the ultimate load-bearing capacity of a superimposed shear wall can reach or exceed that of an entire cast-in-place concrete shear wall under higher axial load ratios because the concrete strength of a preformed layer is higher than that of a cast-in-place layer. Simulations adopting two different models and OPENSEES finite element software were performed to support the theoretical results. These two models included multi-vertical line element model and fiber section model. The simulated results verified the correctness of the theoretical derivation, it was shown that the superimposed shear wall with prefabricated boundary element not only is convenient to make but also has a higher ultimate load-bearing capacity than the superimposed shear wall with cast-in-place boundary element does under higher axial load ratios; so the superimposed shear wall with prefabricated boundary element is more valuable in actual applications.

Key words:building industrialization; superimposed shear wall; multi-vertical line element model; fiber section model; axial load ratios

基金项目：上海市科委重大课题(14DZ1202100)

收稿日期：2015-08-17修改稿收到日期：2015-10-29

通信作者余少乐 男，博士生，1987年生

中图分类号:TU375;TU312

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.036

第一作者 杨联萍 女，博士生导师，副总工程师，1960年生

E-mail:yushaole10@163.com