弹性基础上的双层隔振结构声辐射的主动控制

孙　瑶， 杨铁军， 沈　颖， 黄　迪， 吴　磊， 徐　阳

(1.哈尔滨工程大学 动力与能源工程学院，哈尔滨　150001； 2.江苏城乡建设职业学院,江苏 常州 213147)

弹性基础上的双层隔振结构声辐射的主动控制

孙瑶1， 杨铁军1， 沈颖2， 黄迪1， 吴磊1， 徐阳1

(1.哈尔滨工程大学 动力与能源工程学院，哈尔滨150001； 2.江苏城乡建设职业学院,江苏 常州 213147)

摘要：采用阻抗导纳法建立了以弹性矩形板为基础的双层主动隔振系统数学模型。以基础向外的声辐射为控制对象，探讨不同前馈控制策略的声辐射主动控制效果。分别选取两种面向振动及两种面向声辐射的控制性能函数，考察施加控制后弹性基础的辐射声功率，并综合考虑声压分布及控制力幅值等参数对控制效果进行全面地分析比较，进而评价各控制策略的优劣。结果表明，由于结构振动的耦合作用，面向振动的控制策略会恶化某些频段基础向外的辐射声功率，而直接面向声辐射的控制策略则可能会以放大振动响应或需要大的控制力为代价。最后，还对控制力作用位置对控制效果的影响进行了探讨。

关键词：双层隔振；弹性基础；声辐射；主动控制

隔振结构被广泛应用于隔离动力机械的振动。相对于高频段隔振量随频率上升幂指数地增长，被动隔振在低频段很难获得令人满意的振动隔离效果。对于低频激励，隔振区域的拓宽需要以牺牲被隔振设备稳定性作为代价。在寻求更有效的被动隔振改进方案的同时，大批学者也对主动控制技术在隔振结构中的应用进行了探讨。初期的研究集中于对安装于刚性基础的主动隔振系统进行控制策略分析，而对于基础非刚性的情况(例如船体结构或飞机外壳)，基础结构的振动被证明会对主动隔振的有效性产生影响。Huang[1]采用仿真及实验方法以单层隔振系统为对象，研究了基础弹性对分散速度反馈控制稳定性及控制效果的影响。分析结果表明，基础的弹性不会影响分散反馈控制系统的稳定性，但会导致某些频率下振动的恶化。Yang[2]针对ISVR的主动隔振演示台架建立了任意边界条件下基础弹性板上的单层隔振模型，计算了作动器安装前后的结构振动响应并与实验结果对比，分析作动器的质量效应对主动隔振系统控制效果的影响。对于双层隔振结构，Niu[3]以功率流为控制目标考虑了不同作动位置对主动控制有效性的影响。基础的弹性一方面对隔振效果及控制的有效性产生影响，另一方面，对于有振动及噪声指标要求的飞机、船舶壳体结构，由隔振系统振动产生的基础弹性结构的振动及声辐射也受到越来越多的重视。对于隔振系统通过弹性基础向外声辐射的控制方面，Zhang4建立了以简支板为基础的双层隔振系统模型，分别采用隔振结构与基础简支板连接点振动及简支板离散点振动的和作为为控制目标对不同激励形式下的简支板辐射声压控制效果进行了探讨。

对于隔振系统基础声辐射的主动控制，虽然关注点在于作为辐射体的基础弹性结构，但由于存在基础与隔振系统之间的耦合作用，而且作动力常常作用在隔振结构而非弹性基础上，所以诸多对单独梁、板、壳声辐射主动控制的探讨[5-7]并不能够完整地体现耦合系统的动力学特性。因此，有必要针对隔振系统弹性基础声辐射的主动控制策略有效性及控制效果进行研究。

本文建立了一个以任意边界矩形弹性板为基础的双层主动隔振系统的数学模型，以基础向外的辐射声功率作为主要控制目标，选取四种不同的性能函数对耦合结构进行面向声辐射的主动控制研究。旨在对控制机理进行分析，并结合振动功率流及控制力幅值这两项参数对主动隔振系统的性能进行评价。除此之外，本文对不同作动力布置形式对控制效果的影响也进行了分析。

1双层隔振结构基础声辐射

1.1双层隔振系统动力学建模

图1所示为本文研究的弹性基础上的双层隔振系统。该耦合结构由上层和中间质量、弹性基础及连接各子结构的隔振器构成(每层布置四个共八个隔振器)。考虑到结构尺寸的差异，将上层及中间质量简化成刚体，基础视为弹性矩形板，隔振器则采用集中弹簧阻尼来模拟。

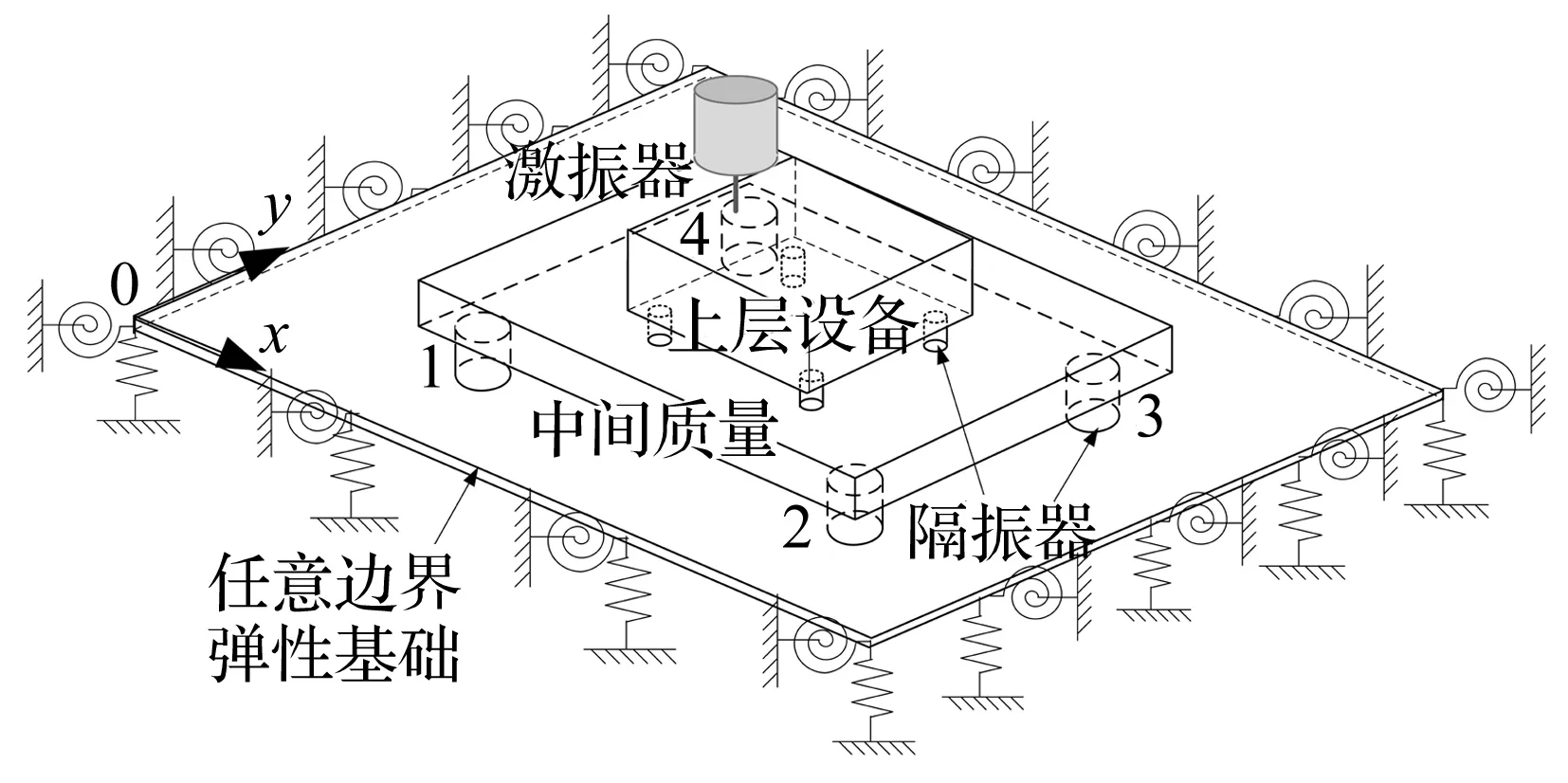
图1　弹性基础双层隔振系统示意图Fig.1 Sketch of a two-stage vibration isolation system

由图2所示双层隔振系统受力情况可列出各子结构平衡方程：

(1)

式中，Ve代表上层质量隔振器安装点的速度向量，Vi1，Vi2分别代表上、下层隔振器在中间质量上安装点的速度向量；Ye、Yi1、Yi2分别表示上层隔振器上端、下端以及下层隔振器上端安装点的原点导纳；Yi2-i1及Zi1-i2分别代表中间质量上下层隔振器安装点之间的跨点导纳和阻抗。Yp-e代表激励点到上层隔振器安装点的跨点导纳；Yb为基础弹性板的导纳矩阵。fp代表外激励力，fm1、fm2分别表示通过隔振器传递的力。

图2　弹性基础双层隔振系统受力分析图Fig.2 Sketch of a two-stage vibration isolation system subjecting to a vertical force

通过求解方程组(1)可以得到通过下层隔振器传递至基础的作用力，其表达式为：

(2)

式中，上下层隔振器的导纳可分别表示为

式中,km1、cm1及km2、cm2分别为上、下层隔振器的刚度及阻尼。

上层、中间质量的原点及跨点导纳Yp-e、Ye、Yi1、Yi2、Yi2-i1及Zi1-i2可由刚体动力学理论求得。首先计算从激励点到刚体质心的导纳，再由质心运动得到刚体上任意一点的运动情况[8]。因结构声辐射主要由其弯曲振动引起，本文仅考虑了产生基础弹性板弯曲振动的隔振系统主要运动成分(竖向振动及绕平面x,y轴的旋转振动)而未计入面内两个方向的平动及面内旋转运动。

基础弹性板上的导纳矩阵Yb可以通过求解振动微分方程来得到。为不失一般性，本文采用改进的傅里叶级数[9]来描述任意边界薄板的振动位移w：

(3)

式中,Amn,am1,am2,am3,am4,bn1,bn2,bn3,bn4为待求系数,Lx、Ly为弹性板的长、宽，ζal、ζbl为辅助函数，其定义同文献[9]。通过对弹性板构建板拉格朗日函数并对各未知系数求导取极值，可以得到9个线性方程组，再采用模态截断，可以得到任意边界弹性板在外激励下的振动响应。这样一方面可以在隔振器安装点施加单位力求得Yb，另一方面结合式(2)可以获得基础板在传递力fm2下的振速分布。

1.2基础板声辐射

假设基础弹性板嵌于无限大障板中，则向其下部空间任意点r′的声压p可以通过瑞利积分基于隔振系统激励下的板表面振速分布来计算：

(4)

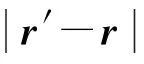
式中：上标H代表共扼转置，Re()表示取实部。

如将基础弹性板分割成M个振动面元(面元的分割应保证面元几何尺寸远小于声波波长)，可对上式进行离散。此时，辐射声功率可以表示成矩阵形式如下：

Wrad=VHRV

(5)

式中V为离散的板表面振速分布向量。R为声辐射阻抗矩阵，其第(m′,n′)个元素可以表示为：

式中,rm′,n′是板上第m′个面元到第n′个面元之间的距离，Δs为每个离散振动面元的面积。根据声辐射模态理论，对声阻抗矩阵R进行特征值分解，可以得到一组特征向量φm′及其相应的特征值λm′。其特征向量被视为结构声辐射的模式即声辐射模态，其对辐射声功率的贡献完全独立；特征值则对应于此阶声辐射模态的辐射效率。

2双层主动隔振耦合系统前馈控制

本文采用前馈控制策略对双层隔振结构弹性基础声辐射的主动控制效果进行分析。前馈控制的特点是待控制的信号与作为控制器输入的参考信号不同，这样可以避免控制信号对参考输入信号的污染而对控制系统的稳定性有益。选取前馈控制的原因一方面是对于动力机械这类周期性激励的控制对象，前馈控制所需的参考信号容易获得；另一方面旨在分析前馈控制机理并寻求能够近似体现隔振系统基础弹性结构声辐射情况的易测参数。本文选取的四种性能函数分别为：① 最小基础弹性板辐射声功率，② 抵消第一阶声辐射模态贡献，③ 最小系统输入功率，④ 最小隔振器安装点平方速度。在上述四种控制策略中，①、②是面向声辐射的前馈控制策略，而③、④是面向振动的前馈控制策略。

2.1最小基础弹性板辐射声功率

当初级力fp及控制力fc共同存在时，基础表面振速分布矩阵V可表示成如下形式：

V=Ypfp+Ycfc

(6)

式中Yp和Yc分别为初级力及控制力到基础弹性板离散点振速的导纳矩阵(由式(2)、(3)确定)，代入声功率表达式(5)中，有

Wrad=fpHYpHRYpfp+fpHYpHRYcfc+

fcHYcHRYpfp+fcHYcHRYcfc

(7)

令a=YcHRYc, b=fpHYpHRYc, c=fpHYpHRYpfp则可将式(7)进一步写为：

Wrad=fcHafc+bHfc+fcHb+c

(8)

根据二次最优理论[10]，对上式求导并取极值可以得到使辐射声功率最小的最优控制力为：

fc,opt=-a-1b

(9)

则使辐射声功率达到最小的最优控制力为，

fc,rad=-(YcHRYc)-1YcHRYpfp

(10)

2.2抵消第一阶声辐射模态贡献

因各阶声辐射模态对辐射声功率的贡献完全独立，换言之，抵消声辐射模态贡献可以有效地控制辐射声功率，这点在很多文献中已有讨论。相关研究指出，抵消N阶声辐射模态贡献需要N个作动力[7]。以抵消第一阶声辐射模态贡献为目标函数为：

W1st=VHφ1φ1HV

继续代入式(6)将上式展开成如式(8)的形式，根据式(9)可得到抵消第一阶声辐射模态贡献策略下的最优控制力表达式为：

(11)

2.3最小系统输入功率

功率流被认为是能够体现系统能量传递的参数[11]，诸多主动控制策略以功率流为目标函数并取得了很好的控制效果[12]。采用输入功率作为噪声主动控制性能函数的思想是出于降低输入系统的能量以达到降低结构声辐射的目的。耦合系统的总输入功率为

Pin(ω)Re(FextVinH)/2

(12)

此处，Fext代表外部力向量(包括激励力及控制力)，即Fext=[fp,fc]T；Vin为外部激励作用点的速度向量，且有

其中Ypp、Ycc分别为激励力及控制力作用点的原点导纳，而Ypc表示两者之间跨点导纳且有Ypc=Ycp。

同样根据二次最优理论，可以得到此控制策略下的最优控制力为：

fc,in=-Rcc-1Rcpfp

(13)

式中，Rcc及Rcp分别为Ycc及Ycp的实部。

2.4最小隔振器安装点平方速度

速度的平方本质上体现了结构的动能，而辐射声能是动能的一部分，这种策略旨在以有限个点的振速平方近似代表基础板的动能。选取下层隔振器在基础弹性板上四个安装点的振速Vb为评价点，此时目标函数的表达式为：

(14)

式中，Vb可视为由初级力及控制力共同作用的结果，即

Vb=Yp-bfp+Yc-bfc

式中，Yp-b、Yc-b分别为从激励力和控制力到下层隔振器在基础弹性板上安装点的导纳矩阵。进一步改写式(14)并采用二次最优法，可得到此控制策略下的最优控制力表达式：

fc,sq=-[Yc-b(Yc-b)H]-1Yc-b(Yp-b)Hfp

(15)

3主动控制效果讨论

如果作动力数目与隔振器数目相同，对于本文建立的弹性基础上的双层隔振结构，理论上基础的振动是完全可以被抵消的。因此文中仅采用一个作动力进行前馈控制可行性及有效性的研究。作动力位置位于上层1号隔振器在中间质量上的安装点。

弹性基础双层隔振结构参数为：上层质量尺寸为0.45 m×0.3 m×0.025 m，中间质量0.7 m×0.45 m×0.03 m，基础板尺寸为1 m×0.8 m×0.005 m，材料均为钢，密度为7 800 kg/m3，弹性板泊松比为0.3，杨氏模量为2.1×1011Pa，基础弹性板的边界条件为固支边界。上层隔振器的刚度为km1=4×105N/m，阻尼cm1=30 Ns/m；下层隔振器的刚度km2=1×106N/m，阻尼cm2=20 Ns/m；隔振器的安装位置列于表1中。此外，初级激励力fp位于上层质量(0.1 m, 0.1 m)处。

表1　隔振器安装位置

3.1不同控制策略的控制效果

分别将两种面向声辐射及两种面向振动的控制策略控制前后的辐射声功率曲线绘制于图3(a), (b)中。

3.1.1基础弹性板辐射声功率

从图3(a)中可以看出，因最小辐射声功率策略以其自身作为性能函数，所以该控制策略在全频段都能获得声辐射能量的衰减。相比之下，抵消第一阶辐射声功率贡献策略对总声功率的控制效果不及最小辐射声功率策略，但除在特定频率下出现恶化，也能取得良好的控制效果。理论上抵消第一阶声辐射模态贡献不会影响其它阶声辐射模态对辐射声功率的贡献。但对于本文讨论的耦合结构，由于子结构及隔振器之间的耦合作用，并且作动力数目小于隔振器数目，因此无法保证基础振速分布与声辐射模态形状正交，这意味着无法只控制一阶声辐射模态而不改变其它声辐射模态对辐射声功率的贡献。

对于两种面向振动的控制策略，从图3(b)中可以看出，其控制效果相近，除少数特定频率外均能获得较大的辐射声功率衰减。

图3　四中不同控制策略控制前后辐射声功率变化Fig.3 Radiation powerwith and without 4 different feedforward control strategies

对比图3(a)、(b)可以发现，对于辐射声功率而言，面向声辐射的前馈控制策略的控制效果优于面向振动的前馈控制策略。但由于振动信号容易测量，所以面向振动的控制策略在工程上具有很大的优势。仿真结果表明，用系统振动参数来表征结构的声辐射，虽然并不适用于所有频率，但也具有一定的可行性。即输入功率流或基础速度平方的降低可以大致地体现基础向外辐射声功率的衰减。

3.1.2声压指向性

在考虑结构总辐射声功率的基础上，考察不同控制策略对声压指向性的影响。选取激励频率为100 Hz，声压基准面设为基础弹性板的下半无限空间中垂直于板平面位于y方向1/2处的半无限平面。将以基础板中心为圆心，在基准面上半径为2 m的半圆的声压指向性绘制于图4中(为符合视图习惯，将结果翻转至上半平面显示)。

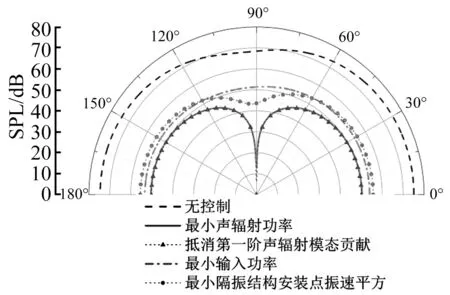
图4　100 Hz激励时不同控制策略对声压指向性的控制效果Fig.4 The variation of sound directivity with excitation of 100 Hz after control

从图4可以看出四种控制策略均能获得全角度的控制效果，并且面向声辐射的控制策略使系统明显体现出偶极子声源的声压辐射特性，而抵消第一阶声辐射模态贡献策略能在90°方向获得最优的声压控制效果。

3.1.3振动功率流

为避免出现振动功率在控后大幅增加的情况，将控制前后传递至基础的振动功率流的变化绘于图5。从图中可以看出，对于传递功率流而言面向振动的控制策略明显优于面向声辐射的控制策略。两种面向声辐射的控制策略在某些频段(30 Hz～50 Hz)放大了传递至基础的功率，这意味着控制声辐射有可能会引起结构振动的恶化。特别是选择抵消第一阶声辐射模态贡献策略时，传递功率流的恶化程度更加显著。

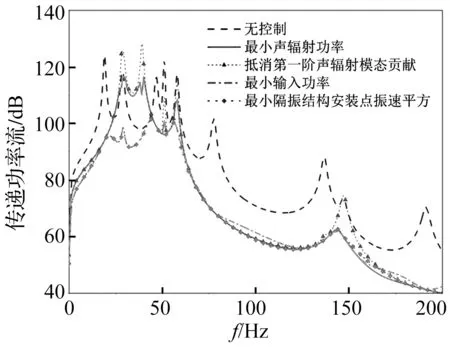
图5　不同控制策略对传递功率流的控制效果Fig.5 Control performance on transmitted power flow

3.1.4作动力幅值

另一个在振动主动控制中倍受关注的因素是所需作动力的幅值。图6绘制了各种控制策略下所需主动控制力与初级激励力的比值随频率的变化情况。从图6中可以看出，面向声辐射的控制策略相对于面向振动的控制策略需要更大的作动力，如在40 Hz附近最小声辐射功率策略需要10倍于初级力的控制力，而对于抵消第一阶声辐射模态贡献策略则需要100倍于初级力的控制力，这在工程中不易实现，即使能实现也需要很大的成本。

图6　不同控制策略所需的控制力幅值Fig.6 Control force for different control strategies

3.2作动器布置对控制效果的影响

本节将就不同作动位置、不同前馈控制策略的控制效果及所需控制力大小进行讨论。除3.1节中讨论的作动力作用于中间质量的情况，本节对作动力作用于上层隔振器的两端、下层隔振器的两端及直接作用于基础弹性板下层隔振器安装点的情况进行了分析。

3.2.1控制力作用于上层隔振器两端

从图7可以看出，当控制力作用于上层隔振器的两端时，除最小输入功率策略外其余控制策略均能获得全频段的控制效果。最小辐射声功率策略虽能获得最大的辐射声功率衰减，但是其对传递功率流的衰减不及最小隔振结构安装点振速平方策略。各种策略的控制效果对比分析列于表2中。

表2　控制力位于上层及中间1点各性能函数控制效果分析

图7　作动力作用于上层及中间质量Fig.7 Control performance for different control force locations

3.2.2控制力作用于下层隔振器两端

作动力作用于下层1号隔振器两端时各策略控制效果如图8所示。

此时抵消第一阶声辐射模态贡献策略对于辐射声功率及传递功率流产生了放大作用，这种放大作用对传递功率流尤其明显。表3总结了这种作动力布置方式时各控制策略的控制效果。

表3　控制力位于中间及基础1点各性能函数控制效果分析

3.2.3控制力作用于基础弹性板

最后，当作动力直接作用于基础时，从图9可见，抵消第一阶声辐射模态贡献策略恶化了特定频段的控制效果。并且统观各控制效果产生的声辐射衰减可以发现，作动力直接作用于基础产生的控制效果比作动力作用于双层隔振结构上差。此外，对于面向声辐射的控制策略，由其改变振动形态从活塞声源-双极子声源的控制机理，在非常低的频率，引起了振动功率的大幅度上升。此作动位置时各种控制策略的控制效果见表4。

表4　控制力位于基础1点各性能函数控制效果分析

图8　控制力同时作用于中间质量及基础Fig.8 Control force acts on intermediate masses and flexible base

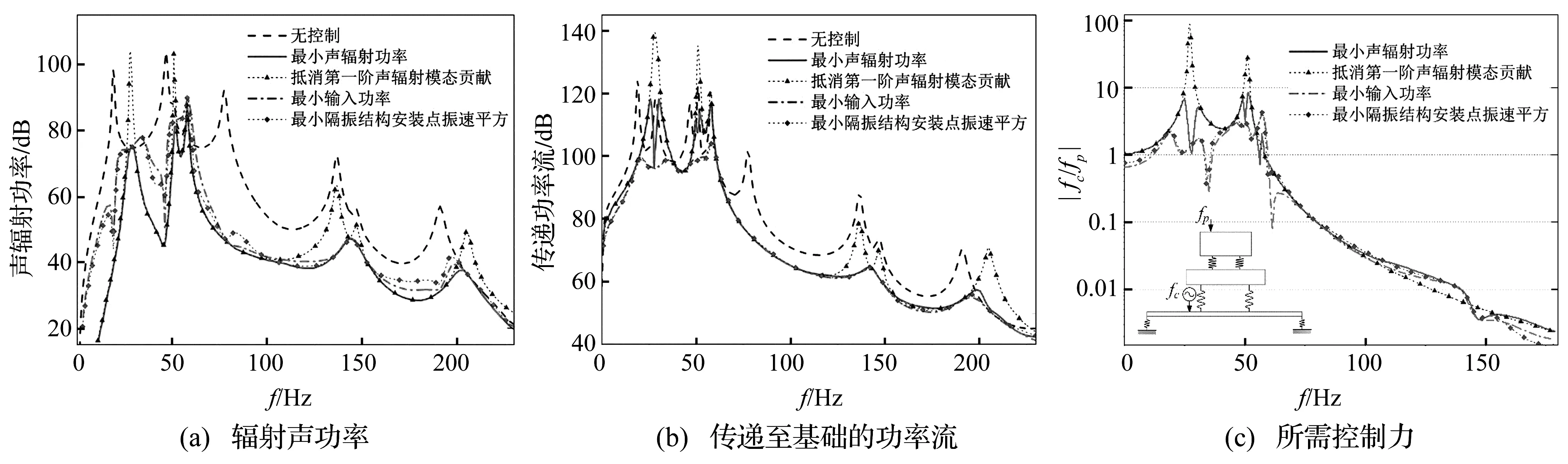
图9　作用力作用于基础Fig.9 Control force acts on flexible base

4结论

本文以弹性基础上双层隔振结构为研究对象分析了四种不同性能函数的前馈控制对基础声辐射的控制效果，并结合传递功率流及所需作动力大小对控制策略进行了评价。此外，对作动力位置对控制效果的影响进行了讨论。仿真分析结果表明：

(1) 对于辐射声功率，面向声辐射前馈控制策略的控制效果优于面向振动的控制策略。但基于参数易测性的考虑，以系统振动响应的降低来表征结构声辐射虽然不能适用于所有频率，但也具有可行性。

(2) 对于作动力数目少于隔振器连接点数目的耦合结构，抵消声辐射模态贡献策略不能够只消除特定阶对应的声功率而不引起其他阶声辐射模态对应声功率的变化。此外，纵然可以获得很好的辐射声功率及声压衰减，此策略存在增大传递功率及需要很大作动力的缺点。

(3) 当作动力作用在上层隔振器两端时，最小输入功率策略会引起辐射声功率在高频段控制效果的恶化。对于本例，作动力作用于隔振结构时的控制效果优于控制力作用于基础。

(4) 综合四种不同性能函数及不同作动形式的仿真结果可以看出：最小隔振器安装点振速平方策略在四种性能函数中对声辐射功率、传递功率流的控制效果都较好并且所需控制力也都在合理范围内。此时作动力作用于中间质量及作用于下层隔振器两端优于其他两种作动位置配置。

参 考 文 献

[1] Gardonio P,Elliott S J, Pinnington R J.Active isolation of structural vibrationon a multipledegree-of-freedom system,part I:the dynamics of the system[J].Journal of Sound and Vibration,1997,207(1):61-93.

[2] Yang T,Brennan M J,Du J,et al. Modeling and vibration analysis of an active vibration isolation demonstration rig[C]//10th International Conference on Recent Advances in Structural Dynamics,Southampton,2010.

[3] Niu Jun-chuan,Song Kong-jie,Lim C W.On active vibration isolation of floating raft system[J].Journal of Sound and Vibration,2005,285:391-406.

[4] Zhang Zhi-yi, Chen Yong, Yin Xue-wen, et al.Active vibration isolation and underwater sound radiation control[J].Journal of Sound andVibration,2008,318:725-736.

[5] Pan J,Snyder S D,Hansen C H,et al.Active control of far field sound radiated by a rectangular panel-A general analysis[J].The Journal of the Acoustical Society of America,1992,91:2056-2066.

[6] 陈克安,尹雪飞. 基于近场声压传感的结构声辐射有源控制[J].声学学报,2005,30(1):63-68.

CHEN Ke-an, YIN Xue-fei.Active control of radiated sound using near field pressure sensing[J].Journal of Acoustics,2005,30(1):63-68.

[7] 毛崎波,姜哲. 通过声辐射模态研究结构声辐射的有源控制[J].声学学报,2001,26(3):277-281.

MAO Qi-bo, JIANG Zhe.A research on active sturctural acoustic control by radiation modes[J].Journal of Acoustics,2001,26(3):277-281.

[8] Ananthaganeshank A.Stability and performance of active vibration isolation systems[D].University of Southampton,2002

[9] Li W L,Zhang Xue-feng,Du Jing-tao,et al.An exact series solution for the transverse vibration of Rectangular plates with general elastic boundary supports[J].Journal of Sound and Vibration,2009,321:254-269.

[10] Fuller C R,Elliott S J,Nelson P A.Active control of vibration[M].London: Academic Press,1996.

[11] 宋孔杰,张蔚波,牛军川.功率流理论在柔性振动控制技术中的应用与发展[J].机械工程学报,2003,39(9):23-28.

SONG Kong-jie,ZHANG Wei-bo,NIU Jun-chuan,Application and development of power flow theories in the field of the vibration control for flexible systems[J].Journal of Mechanical Engineering,2003,39(9):23-28.

[12] Pan J Q, Hansen C H.Active control of Power flow from a vibrating rigid body to a flexible Panel through two active isolators[J].The Journal of the Acoustical Society of America,1993,94 (3):1947-1953.

Active noise control for sound radiated from flexible base of a two-stage vibration isolation system

SUN Yao1, YANG Tie-jun1, SHEN Ying2, HUANG Di1, WU Lei1, XU Yang1

(1. Power and Energy Engineering College, Harbin Engineering University, Harbin 150001, China;2. Jiangsu Institute of Urban and Rural Construction, Changzhou 213147, China)

Abstract:In order to evaluate control performances of different feed-forward control strategies for sound radiated from the flexible base of a two-stage vibration isolation system, a mathematical model of a two-stage vibration isolation system mounting on an elastic rectangular plate was established. Two vibration-oriented cost functions and two sound radiation-oriented ones were chosen and the acoustic radiation power of the plate after control was investigated. Further more, the control effects were comprehensively analyzed by taking parameters like sound pressure distribution, and control force amplitude into account. Then the advantages and disadvantages of different control strategies were evaluated. The simulation results showed that the vibration oriented control strategies may lead to increase in the radiated sound power at specific frequencies while the sound radiation-oriented control strategies may amplity vibration responses and need a larger control force amplitude. In addition, the influence of the location of control force on the control effect was studied.

Key words:two-stage vibration isolation; flexible base; sound radiation; active control

基金项目：国家自然科学基金项目(51375103)

收稿日期：2015-03-09修改稿收到日期：2015-05-11

通信作者杨铁军 男，博士，教授，1972年10月生

中图分类号:O328

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.032

第一作者 孙瑶 女，博士生，1987年1月生