高层建筑动态位移摄像测量环境影响及自适应滤波降噪研究

秦良忠， 周华飞， 卢成原， 胡雪兵， 谢子令

(1. 浙江工业大学 建筑工程学院，杭州　310014； 2. 温州大学 建筑工程学院，温州　325035)

高层建筑动态位移摄像测量环境影响及自适应滤波降噪研究

秦良忠1， 周华飞2， 卢成原1， 胡雪兵2， 谢子令2

(1. 浙江工业大学 建筑工程学院，杭州310014； 2. 温州大学 建筑工程学院，温州325035)

摘要：位移是反映结构性能和安全的重要指标。大型结构动态位移监测仍存在较多困难。摄像测量具有非接触、低成本等突出优点，有望成为一种实用方法，但其全天候工作性能评估及优化有待研究。开展了高层建筑动态位移全天候摄像测量长期室外试验，并以降雨天气下的位移实测数据为研究对象，分析了降雨对摄像测量精度的影响。降雨对摄像测量产生了显著影响，导致位移测量精度明显降低。为拓宽摄像测量的适用环境，提出了采用自适应滤波方法进行降噪处理。结果表明，自适应滤波方法能有效地去除测量噪声，提高摄像测量在暴雨环境下的测量精度，为实现高层建筑动态位移全天候摄像测量提供了必要条件。

关键词：高层建筑；动态位移；摄像测量；环境影响；自适应滤波

位移是反映结构性能和安全的重要指标。结构位移监测已有许多方法，如：全站仪、LVDT位移传感器、加速度传感器、全球定位系统等。然而，它们不能完全满足大型结构动态位移监测的需要。人工读数全站仪不适用于动态位移监测，而自动化全站仪的目标跟踪受到结构变形幅度不宜过大的限制，且易受环境影响。LVDT位移传感器是一种接触型传感器，要求不动基准点限制了它在建筑水平位移、桥梁挠度监测方面的应用。加速度传感器属于间接测量方法，通过对加速度的二次积分求位移。虽然加速度传感器的精度很高，但是数值积分引起的累积误差较大。全球定位系统(GPS)竖向位移测量精度较低，且易受卫星信号遮挡、电磁干扰、多路径效应等影响。可见，精确实用的大型结构动态位移监测方法仍非常欠缺。

近年来，摄像测量已成为结构监测领域的研究热点，有望成为一种精确实用的大型结构动态位移监测方法。它利用摄像机或照相机等对景/物进行拍摄得到数字图像，再应用数字图像处理分析技术并结合目标三维信息的求解和分析算法，对目标的结构参数或运动参数进行测量和估计[1]。20世纪90年代初，国外出现了结构位移摄像测量方法的应用。Stephen等[2]提出了采用视觉跟踪系统测量桥梁跨中位移，并测量了英国Humber大桥的低频运动。Lee等[3-4]在一桥梁荷载试验中采用了数字摄像机监测位移，摄像测量结果与激光测振仪结果吻合较好。Caetano等[5]采用了数字摄像系统测量斜拉桥的斜拉索振动，当数字摄像机与拉索之间的直线距离为850 m时，可测得振幅为8～10 cm的振动，并可识别得到斜拉索的低阶振动模态。近十年来，国内也出现了结构位移摄像测量方法的应用。何振星和于起峰[6]结合远距离摄像和图像处理方法测量桥梁位移，并应用于某梁桥和钢架拱桥的静载和动载试验。罗洪斌等[7]将CCD图像监测系统应用于某立交桥动载试验的动位移测量。姜欣等[8]将摄像测量用于路面平整度检测，通过摄像机亚像素定位标志点的位置变化来测量路面的起伏变化。陈伟欢等[9]利用数码摄像技术对广州新电视塔动态位移进行了实时监测，并与GPS测得的动态位移数据进行比较。李鹏辉等[10]开发了基于数字图像处理技术的多点动态位移测量系统，采用磁盘阵列和同步信号发生器保证海量数据处理和多路相机之间的同步，设计了4层钢结构框架振动台试验进行验证。

至今，结构位移摄像测量的实际工程应用仍以短期现场测试为主。由于缺乏科学的可应用性评估依据和方法，一般根据经验选择合适的时机(尽量避开各种不利环境)进行现场试验，导致测量结果存在较多不确定性。然而，全天候实时监测结构的动态特性对结构的安全评估尤为重要，特别是台风、暴雨、大雪等不利环境下。降雨是最常见的气候现象之一，也是摄像测量的最不利环境影响因素之一。它能使大气中的光信号发生衰减，给摄像测量带来噪声，由此测得的结构位移数据往往包含降雨等不利环境产生的噪声。大跨度桥梁或者高层建筑物的动态位移监测距离一般为几十米至几百米，甚至上千米，因此，研究降雨对远距离摄像测量的精度影响及噪声消除方法是必要且有意义的。

基于上述分析，作者开展了高层建筑动态位移全天候摄像测量试验，以评估摄像测量系统在不利环境影响下的工作性能及测量精度。自2013年9月开始试验至今，已监测得到数次台风、暴雨等不利环境下的位移监测数据。本文针对高层建筑动态位移，分析了降雨对摄像测量系统的精度影响，并提出了采用自适应滤波方法进行降噪处理。结果表明，降雨对摄像测量将产生显著影响，导致位移测量精度降低。自适应滤波方法能有效去除降雨引起的噪声，提高结构位移摄像测量系统在暴雨环境下的测量精度。

1试验设计

1.1位移模拟装置

由于真实结构的位移真实值不得而知，故自主设计了一套位移模拟装置来产生虚拟结构动态位移。该装置主要由两根相互垂直的铝合金梁和LED标靶组成，如图1所示。横梁固定不动，为纵梁的水平运动提供轨道。横梁上还固定了一个静态LED标靶，作为位移参考点。纵梁可沿横梁水平运动，以模拟结构的水平位移。动态LED标靶可沿纵梁竖向运动，以模拟结构的竖向位移。纵梁水平运动和动态LED标靶竖向运动的组合则可产生任意的平面运动。位移模拟装置通过微机控制产生虚拟结构动态位移，用户可通过位移模拟软件输入虚拟结构动态位移的运动参数，包括结构的运动轨迹、频率、幅值等。

图1　位移模拟装置Fig.1 Virtual displacement generation device

1.2结构位移摄像测量系统

结构位移摄像测量系统主要包括工业数字摄像机及变焦镜头、千兆网卡的笔记本电脑、以及自开发的系统软件，如图2所示。工业数字摄像机为Prosilica GigE的GE1050，像素为1024×1024，最高采样频率为60 Hz，变焦镜头的焦距为900 mm，能对几百米甚至上千米的景/物进行监测。自开发的系统软件能实时分析和储存监测目标两个垂直方向的位移变化。

图2　工业数字摄像机Fig.2 Industrial digital camera

结构位移摄像测量方法的流程为：首先，在位移测点安装标志点(摄像机的跟踪目标)，并选取合适的不动点架设摄像机。受益于非接触和远距离的优点，摄像机可架设在结构外的不动点，从而克服了接触式位移测量方法的不足。然后，对物空间坐标系统和像平面坐标系统进行标定。标定完成后，即可开始采集标志点的序列图像。基于数字图像，采用数字图像处理分析技术获取标志点的像素坐标，并利用标定关系换算得到标志点的空间坐标。对于每帧数字图像，重复上述分析，即可得到标志点的位移时程曲线。

系统标定是获取摄像机内外参数的过程。假设物体上一点P经过摄像机镜头摄影后成像到像平面上，其空间坐标与像坐标之间通过小孔成像模型相关联：

λx=K[Rt]X=HX

(1)

式中：X=[Xw,Yw,Zw,1]T∈R4，x=[u,v,1]T∈R3分别表示点P在世界坐标系中的齐次坐标，以及它在像平面坐标中的像素齐次坐标；λ∈R为尺度因子；H=K[Rt]为摄像机的内外参数，其中，R∈R3×3与t∈R3分别为旋转矩阵和平移向量，即摄像机的外参数，K∈R3×3为摄像机的内参数，其具体形式如下：

(2)

式中：(u0,v0)为主点坐标；fx，fy分别表示图像平面坐标系中u方向和v方向的等效焦距；s为倾斜因子，即像素坐标系中两个坐标轴之间的夹角。在理想情况下，两坐标轴正交，其倾斜因子近似为0。

进行系统标定时，由于图像点P在像平面的坐标仅依赖于像坐标系的选择而与世界坐标系的选择无关，因此可以自由选择世界坐标系。若将世界坐标系的原点选择在标定板平面上，且Z轴与该平面垂直，则目标点P的世界坐标为X=[Xw,Yw,0,1]T∈R4，将其代入式(1)整理可得：

(3)

式中，旋转矩阵R化简为3×2维矩阵。在摄像系统标定过程中，标定点的世界坐标X可从标定板上直接读取得到，其像坐标x可由数字图像处理软件分析得到。根据式(3)可知，每个已知坐标的标定点均可列出三个独立的方程，若给定四对以上的图像匹配点，便可求得摄像机的内外参数[11]。

本试验利用位移模拟装置标定结构位移摄像系统。首先，将动态LED标靶移动至用户指定的任一位置，其空间坐标已知，利用摄像机采集动态LED标靶的图像获取该标志点的像素坐标，即可得到一对图像匹配点。然后，将动态LED标靶移动至用户指定的另一位置，同理，可以得到另一对图像匹配点。如此重复，得到四对以上图像匹配点后，将其代入式(3)，便可求得摄像机的内外参数，从而完成结构位移摄像测量系统的标定。

1.3现场实测

在温州大学校园内建立了室外、自动、连续、长期的动态位移摄像测量系统，由位移模拟装置产生动态位移，由工业数字摄像机实时监测。在综合考虑摄像机和位移模拟装置的防盗保护、视线通道、行人车辆干扰等实施关键问题后，将场地选择在一幢五层教学楼屋顶上，如图3所示。该建筑物楼层较低且水平刚度较大，几乎不发生水平向位移。位移模拟装置安装在该建筑物的东北角，工业数字摄像机布置在西南角，两者之间的距离为95.6 m。已有的摄像测量现场实测研究中，其中一部分的测试距离也在百米左右，如：Lee等[3-4]进行桥梁荷载试验时，测试距离为20 m；何振星和于起峰[6]对大中跨径桥梁进行动态位移监测时，测试距离为50 m至100 m；范绪奇等[12]对广州一幢高层住宅楼进行动态位移监测，测量距离约为80 m。因此，本文的试验距离对现场实测工作具有参考意义。

图3　试验场地Fig.3 Experiment site

本文以高层建筑的虚拟动态位移为例进行分析。高层建筑在风荷载作用下，位移主要发生在水平向，而竖向位移极小。因此，在位移模拟装置中将水平向位移函数设置为一正弦函数，将竖向位移函数设置为零。根据《建筑结构荷载规范》GB 50009-2012[13]，钢筋混凝土高层建筑的基本自振周期为T=(0.05～0.10)n，其中，n为建筑物层数。若取n为100，则可将水平向位移函数设置为周期为10 s、幅值为20 mm的正弦函数，如图4所示。结构位移摄像测量系统的采样频率设置为10 Hz。位移模拟装置中的微机界面可利用结构位移摄像测量系统中的TeamViewer软件远程控制，并采用同步触发软件实现位移模拟装置与摄像测量系统之间的同步。

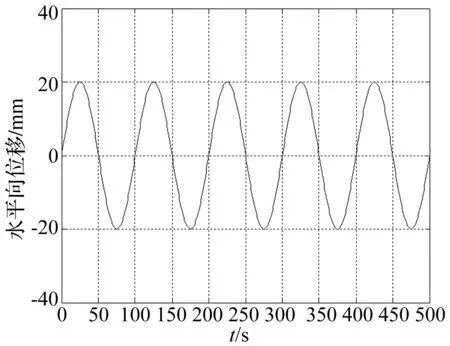
图4　虚拟结构水平向位移Fig.4 Virtual structural horizontal displacement

2试验结果

2.1晴朗天气

图5　晴朗天气下水平向和竖向实测位移时程Fig.5 Time histories of horizontal and vertical displacements measured under fine weather conditions

图5为在某晴朗天气所测得的水平向和竖向位移时程。由图5(a)可见，水平向位移的测量结果与水平向真实位移基本吻合。由于动态LED标靶只做水平向简谐运动，故图5(b)中的竖向位移测量结果可近似视为测量噪声。类似地，将水平向位移实测结果减去其真实位移值，即可得到水平向位移的测量噪声，如图6所示。水平向和竖向位移的测量噪声的最大值仅为1.01 mm和0.66 mm，平均值仅为0.25 mm和0.13 mm。图7为水平向和竖向位移的测量噪声的概率分布。由图可见，水平向和竖向位移的测量噪声均较好地服从高斯分布。因此，晴朗天气下，结构位移摄像测量系统的测量噪声较小，且服从高斯分布。

图6　晴朗天气下水平向位移的测量噪声Fig.6 Noises of measured horizontal displacements under fine weather conditions

图7　水平向和竖向位移的测量噪声的概率分布Fig.7 Probability distributions ofnoises of horizontal and vertical displacements

为了探讨测量距离对摄像测量噪声的影响，本文还进行了一些短期的远距离试验。图8为在某晴朗天气进行远距离试验的水平向和竖向位移时程。摄像机对地面的不动标志点进行监测，两者之间的距离为307.2 m。由于行人及车辆干扰，有效的测量数据时段较短。表1为该时段内的摄像测量噪声的统计分析，并与距离为95.6 m时的测量噪声值进行比较。可见，当测量距离由95.5 m增加至307.2 m时，水平向和竖向测量噪声明显增大。图9为水平向和竖向位移测量噪声的概率分布图。可见，当测量距离为307.2 m时，水平向和竖向位移的测量噪声仍较好地服从高斯分布。因此，测量距离的增加，将增加噪声的大小，但并不改变噪声的性质。

图8　远距离试验的水平向和竖向实测位移时程Fig.8 Time histories of horizontal and vertical displacements measuredin a long-distance test

噪声/mm(取绝对值)测量距离95.6m最大值平均值测量距离307.2m最大值平均值晴朗天气水平向1.010.251.840.38竖向0.660.131.200.25

图9　远距离试验的水平向和竖向位移的测量噪声的概率分布Fig.9 Probability distributions of noises of horizontal and vertical displacements in a long-distance test

2.2雷阵雨天气

图10为2014年7月21日17时至19时的水平向和竖向实测位移时程。同样地，图10(b)中的竖向位移测量结果可近似视为竖向位移的测量噪声。图11为水平向位移的测量噪声。当日下午17时10分开始下雷阵雨，期间雨量较大，18时30分左右雨量逐渐减小，至18时50分降雨停止。由图可知，雷阵雨之前，结构位移摄像测量系统测得的水平向和竖向位移的噪声值均较为稳定。阵雨期间，两者的噪声值均出现较大起伏，噪声最大值分别达到10.38 mm和9.10 mm。降雨减小或停止后，噪声值又再次趋于稳定。鉴于阵雨期间水平向与竖向位移的测量噪声呈现较好的相关性，故对它们进行相关性分析，相关系数可由下式计算，即：

(4)

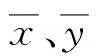
图10　雷阵雨天气下水平向和竖向实测位移时程Fig.10 Time histories of horizontal and vertical displacements measured under thunderstorm conditions

图11　雷阵雨天气下水平向位移的测量噪声Fig.11 Noises of measured horizontal displacement under thunderstorm conditions

表2为晴朗天气与雷阵雨天气下水平向和竖向位移的测量噪声值比较。雷阵雨天气下，水平向和竖向位移的测量噪声的最大值分别达到10.38 mm和9.10 mm；平均值分别达到3.60 mm和2.99 mm，远大于晴朗天气下水平向和竖向的测量噪声。因此，结构位移摄像测量系统在雷阵雨天气下将产生较大的测量噪声，有必要对结构位移的实测结果进行降噪处理。

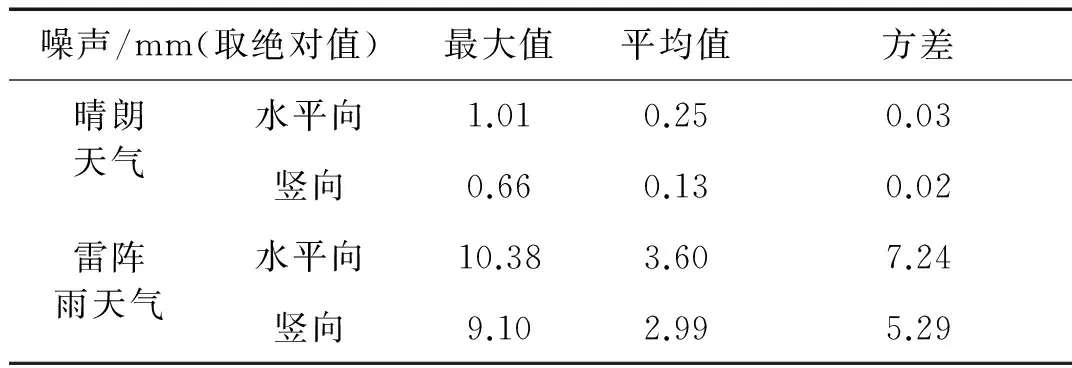
表2　晴朗天气与雷阵雨天气下水平向

3自适应滤波降噪

在同一试验中，由于试验条件及环境相同，竖向位移实测结果(可近似为测量噪声)与水平向位移实测结果中包含的测量噪声相关，但与水平向位移实测结果所包含的真实位移不相关，满足自适应滤波器的应用条件。因此，本文采用自适应滤波算法对水平向的位移实测结果进行降噪处理。

3.1自适应噪声抵消器原理

自适应噪声抵消器原理结构图如图12所示。图中基本信号x(n)为有用信号s(n)和干扰噪声v0(n)之和，即x(n)=s(n)+v0(n)，n表示时间序列。参考信号v1(n)是一个与s(n)无关，但与v0(n)相关的噪声信号。自适应滤波器以当前及其前N-1时刻的参考信号为输入矢量，即V1(n)=[v1(n),v1(n-1),…,v1(n-N+1)]，N为自适应滤波器的阶数。通过调节自适应滤波器的权系数矢量W(n)=[w0(n),w1(n),…,wN-1(n)]，可使得输出信号y(n)尽可能逼近x(n)中的噪声v0(n)，此时，y(n)与x(n)之差e(n)就接近于有用信号s(n)。

图12　自适应噪声抵消器原理结构图Fig.12 Adaptive noise cancellation system

自适应滤波器的权系数矢量W(n)采用自适应算法调节。根据优化准则不同，自适应算法大致可分为LMS算法和RLS算法。LMS算法是由Widrow和Hoff在1959年研究自适应线性元素的模式识别方案时所提出的[14-15]，因其具有算法简单、收敛性好、性能稳定等优点，已成为应用最广泛的自适应算法。具体地，基于LMS算法的自适应滤波算法的步骤如下：

① 计算时刻n自适应滤波器的输入矢量与权系数矢量的卷积，得到输出信号y(n)，即

y(n)=V1(n)WT(n)

(5)

② 计算基本信号与输出信号之差，得到误差信号e(n)，即

e(n)=x(n)-y(n)=x(n)-V1(n))WT(n)

(6)

③ 利用最速下降法，得到自适应滤波器在n+1时刻的权系数，即

wk(n+1)=wk(n)+2μe(n)v1(n-k),

k=0,1,…,N-1

(7)

式中：wk(n)和wk(n+1)分别为迭代前后的权系数值；μ为收敛因子，用于控制自适应滤波的收敛速度。

④ 将时刻增加至n+1，重复上述步骤①～③。通过如此迭代更新权系数，最终使得误差信号的均方差E[e2(n)]达到最小。可以证明，当E[e2(n)]为最小值时，E[(v0(n)-y(n))2]取得最小值。此时，输出信号y(n)逼近基本信号中的干扰噪声v0(n)，误差信号e(n)逼近基本信号中的有效信号s(n)。由此可见，自适应滤波方法并非根据信号频率进行滤波，若基本信号与参考信号的某些频率成分相近，频率相近部分的真实信号不会被滤掉。

3.2位移自适应滤波降噪结果

将水平向位移的实测结果作为基本信号，竖向位移的实测结果作为参考信号，输入到自适应噪声抵消器中，可得到滤波后的水平向位移，如图13所示。图14为自适应滤波前后的水平向位移。相对滤波前的水平向位移值，滤波后的水平向位移值更加平滑，且更接近水平向位移的真实值。图15为自适应滤波前后水平向位移的测量噪声。经过自适应滤波降噪处理后，包含在水平向位移数据中的测量噪声明显减小且变化平稳。表3为自适应滤波前后水平向位移的测量噪声比较。经自适应滤波降噪处理后，包含在水平位移数据中的噪声平均值由原来的3.60 mm降至0.71 mm，下降了80.28 %；噪声最大值由原来的10.38 mm降至3.40 mm，下降了67.24 %。上述结果表明，自适应滤波方法能有效地去除包含在位移实测结果中的测量噪声，提高结构位移摄像测量系统在暴雨环境下的测量精度，从而拓宽摄像测量的适用环境，为实现高层建筑动态位移全天候摄像测量奠定基础。

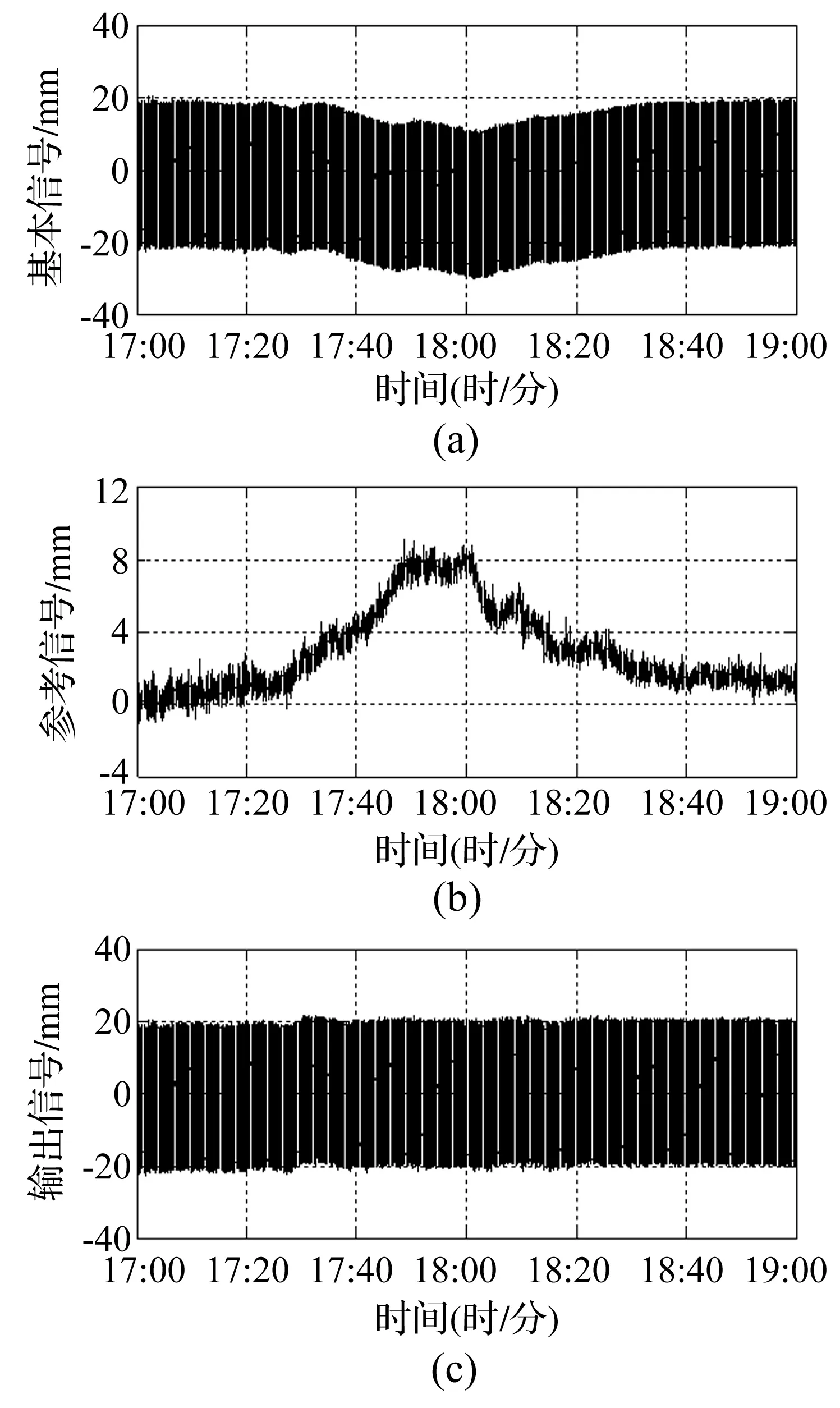
图13　水平向位移自适应滤波降噪结果Fig.13 De-noising of horizontal displacement using adaptive filtering

由于暴雨天气往往具有突发性，通过临时的短期试验不易获得暴雨天气下的摄像测量试验结果。根据晴朗天气所测得的远距离试验结果，测量距离的增加，将增加噪声的大小，但并不改变噪声的性质(随机噪声)。不仅如此，雨雾引起的摄像测量噪声具有显著的系统性。因此，自适应滤波方法应仍能适用于远距离摄像测量中雨雾引起的噪声降噪。

图14　自适应滤波前后水平向位移Fig.14 Horizontal displacements before and after adaptive filtering

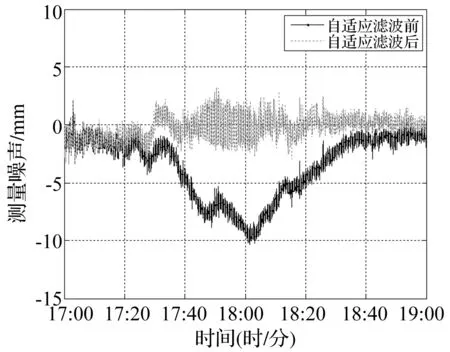
图15　自适应滤波前后水平向位移的测量噪声比较Fig.15 Noises in horizontal displacement before and after adaptive filtering

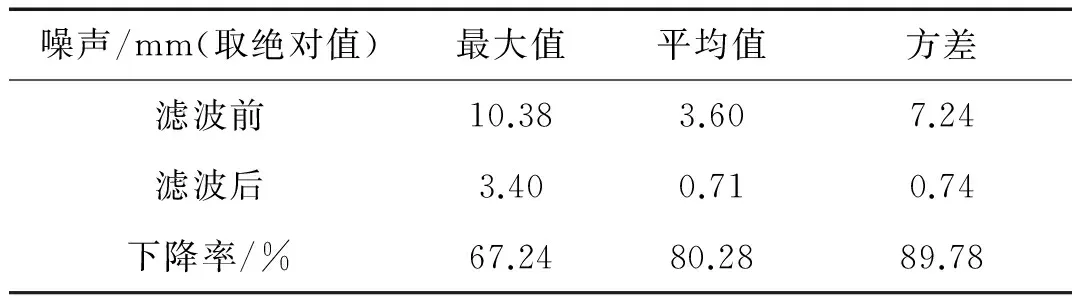
噪声/mm(取绝对值)最大值平均值方差滤波前10.383.607.24滤波后3.400.710.74下降率/%67.2480.2889.78

4结论

本文针对高层建筑动态位移，分析了降雨对摄像测量系统精度的影响，并提出了采用自适应滤波方法对实测数据进行降噪处理，得到以下结论：

(1) 结构位移摄像系统在不同环境影响下的测量精度有所不同。雷阵雨天气下，水平向和竖向位移的测量噪声的最大值分别达到10.38 mm和9.10 mm；平均值分别达到3.60 mm和2.99 mm，远大于晴朗天气下水平向和竖向的测量噪声。

(2) 阵雨期间水平向与竖向位移的测量噪声呈现较强的负相关性，但与水平向位移实测结果所包含的真实位移不相关，这为采用自适应滤波方法进行降噪处理创造了前提条件。

(3) 自适应滤波方法能有效地去除降雨引起的测量噪声，提高结构位移摄像测量系统在暴雨环境下的测量精度。经自适应滤波降噪后，水平向位移的噪声平均值由原来的3.60 mm降至0.71 mm，下降80.28 %；噪声最大值由原来的10.38 mm降至3.40 mm，下降67.24 %。

(4) 测量距离必然对摄像测量的精度产生影响，因此，有必要针对不同的距离分别进行长期室外试验。同时，为了全面客观地分析环境影响，进行一个完整环境变化周期(一年)下的摄像测量试验也是必要的。现阶段，更远距离的摄像测量长期室外试验尚未系统展开，将在后续研究中进行。根据晴朗天气所测得的远距离短期试验结果，测量距离的增加，将增加噪声的大小，但并不改变噪声的性质。因此，自适应滤波方法应仍能适用于远距离摄像测量中雨雾引起的噪声降噪。此外，后续研究还将分析摄像测量系统在台风、大雪、大雾等不利环境下的工作性能，以期拓宽其适用环境，为实现高层建筑动态位移全天候摄像测量提供必要条件。

参 考 文 献

[1] 于起峰，尚洋. 摄像测量学原理与应用研究[M]. 北京：科学出版社，2009.

[2] Stephen G A,Brownjohn J M W,Taylor C A. Measurements of static and dynamic displacement from visual monitoring of the Humber bridge[J]. Engineering Structures,1993,15(3):197-208.

[3] Lee J J,Shinozuka M. A vision-based system for remote sensing of bridge displacement[J]. NDT&E International,2006,39(5):425-431.

[4] Lee J J,Fukuda Y,Shinozuka M,et al. Development and application of a vision-based displacement measurement system for structural health monitoring of civil structures[J]. Smart Structures and Systems,2007,3(3):373-384.

[5] Caetano E,Silva S,Bateira J. Application of a vision system to the monitoring of cable structures [C]//Proceedings of the 7th International Conference on Cable Dynamics,2007,Wien,Austria.

[6] 何振星，于起峰. 桥梁位移的远距离测量新技术[J]. 广东公路交通，2003，4：21-23.

HE Zhen-xing,YU Qi-feng. The new technology of remote measurement of bridge displacement[J]. Guangdong Highway Communications,2003,4:21-23.

[7] 罗洪斌，赵文光，文银平，等. CCD图像监测系统应用于桥梁结构检测[J]. 华中科技大学学报:城市科学版，2006，5(23)：91-93.

LUO Hong-bin,ZHAO Wen-guang,WEN Yin-ping,et al. Application of CCD image monitoring system in detecting bridge structure[J]. Journal of Huazhong University of Science Technology:Urban Science Edition,2006,5(23):91-93.

[8] 姜欣，张小虎，于起峰. 路面平整度摄像测量的应用[J]. 筑路机械与施工机械化，2009(2)：50-52.

JIANG Xin,ZHANG Xiao-hu,YU Qi-feng. Application of photographic measurement of pavement roughness[J]. Road Machinery & Construction Mechanization,2009(2):50-52.

[9] 陈伟欢，吕中荣，陈树辉，等. 基于数码摄像技术的高耸结构动态特性监测[J]. 振动与冲击，2011，30(7)：5-9.

CHEN Wei-huan,LÜ Zhong-rong,CHEN Shu-hui,et al. Monitoring dynamic characteristics of a highrise structure based on digital camera technology[J]. Journal of Vibration and Shock,2011,30(7):5-9.

[10] 李鹏辉，赵文光，朱宏平，等. 基于数字图像处理技术的多点动态位移监测[J]. 华中科技大学学报:自然科学版，2011，39(2)：80-84.

LI Peng-hui,ZHAO Wen-guang,ZHU Hong-ping,et al. Monitoring multi-dynamic displacement by digital image technology[J]. J. of Huazhong Univ. of Sci. & Tech:Natural Science Edition,2011,39(2):80-84.

[11] Hartley R,Zisserman A. Multiple view geometry in computer vision[M]. Cambridge,UK:Cambridge University Press,2000.

[12] 范绪奇，徐冲. 基于数字图像技术的高层结构动态特性监测[J]. 城市建设理论研究，2012，12.

FAN Xu-qi,XU Chong. Monitoring dynamic characteristics of a high-rise structure based on digital image technology[J]. Urban Construction Theory Research, 2012(12).

[13] GB 50009-2012 建筑结构荷载规范[S]. 北京：中国建筑工业出版社，2012.

[14] Wiener N,HoPf E. On a class of singular integral equations[J]. Proc. Prussian Acad. Math-Phys. Ser. 1931:696-697.

[15] Widrow B,Hoff M E. Adaptive switching circuits[J]. IRE WESCON Conv. Rec. Pt. 4. 1960:96-104.

Environmental effects on videogrammetry for dynamic displacement monitoring of high-rise buildings and adaptive filtering for de-noising of displacement measurement data

QIN Liang-zhong1, ZHOU Hua-fei2, LU Cheng-yuan1, HU Xue-bing2, XIE Zi-ling2

(1. College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China;2. College of Architecture and Civil Engineering, Wenzhou University, Wenzhou 325035, China)

Abstract:Displacement is a good index for structural behavior and safety status. However, measuring displacement of structures under dynamic excitations is still a challenging task. Videogrammetry has a great potential for dynamic displacement measurement due to its non-contact and low-cost characteristics. Nevertheless, its all-weather working performance should be fully evaluated and optimized before its wide applications. Here, long-term outdoor dynamic displacement monitoring tests using videogrammetry were conducted. A virtual displacement generation device was fabricated to generate dynamic displacements of various structures and an industrial digital camera was employed to monitor virtual displacements. Here, virtual displacements of high-rise buildings measured under raining conditions were analyzed. It was shown that raining has significant effects on videogrammetry, it obviously reduces the accuracy of displacement measurement data. To widen the applicability of videogrammetry, the adaptive filtering method was proposed to de-noise the displacement measurement data. The results showed that the adaptive filtering is well capable of decreasing or removing measurement noises and improving the accuracy of displacement measurement data; it is helpful for the realization of all-weather videogrammetry for dynamic displacement monitoring of high-rise buildings.

Key words:high-rise buildings; dynamic displacement; videogrammetry; environmental effect; adaptive filtering

基金项目：国家自然科学基金(51208384)；浙江省钱江人才计划(2012R10071)；浙江省自然科学基金(LY12E08009)

收稿日期：2014-12-23修改稿收到日期：2015-05-08

通信作者周华飞 男，博士，教授，1978年生

中图分类号:TU196.4

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.031

第一作者 秦良忠 男，硕士生，1990年生