基于图像形状特征和LLTSA的故障诊断方法

张前图, 房立清

(1.驻356厂军代室，昆明　650114; 2.军械工程学院 火炮工程系，石家庄　050003)

基于图像形状特征和LLTSA的故障诊断方法

张前图1,2, 房立清2

(1.驻356厂军代室，昆明650114; 2.军械工程学院 火炮工程系，石家庄050003)

摘要：针对滚动轴承故障诊断问题，提出了一种基于图像形状特征和线性局部切空间排列(LLTSA)的故障诊断方法。首先采用SDP(Symmetrized Dot Pattern)方法对时域信号进行变换，得到极坐标空间下的雪花图像，在分析图像特点的基础上，从图像处理的角度初步提取出图像的形状特征；然后利用LLTSA对初步提取的特征进行维数约简以提取低维特征；最后采用支持向量机(SVM)对低维特征进行分类评估。滚动轴承的故障诊断实验表明图像形状特征能够表征轴承的状态，经LLTSA约简后特征数据的复杂度得到降低，且具有更好的聚类效果，而SVM对轴承4种状态的识别率也达到了100%，验证了该方法的有效性。

关键词：SDP；形状特征；线性局部切空间排列；支持向量机；故障诊断

滚动轴承是机械设备中最常见、最容易损坏的部件之一，其正常与否决定着机械设备状态的好坏。振动信号作为滚动轴承故障信息的载体，包含着轴承运行状态的重要信息，对其进行分析处理是实现轴承故障诊断的常用方法。目前对振动信号进行分析主要从时域、频域以及时频域等方面入手，采用不同的信号处理方法，提取能够表征轴承运行状态的特征，取得了不错的效果[1-3]。近年来，也有不少学者[4-5]采用相应的方法将振动信号可视化，进而以图像处理的方式，提取出能够表征其运行状态的特征并加以分类识别。目前从图像处理的角度进行故障诊断时，图像的来源大多都是对信号进行时频分析后得到的时频图，但时频变换计算复杂，且从图像提取的特征往往是一些统计特征量，选择没有规律性且计算复杂，易丢失重要的时频信息。

SDP[6-8](Symmetrized Dot Pattern)作为一种图像生成方法，相比于时频分析具有理论简单、运算速度快的特点，能够将一维的时间序列通过相应的计算公式变换到极坐标空间下的对称雪花图，不同信号之间的差异可以通过雪花花瓣形状的不同得以体现。根据这一特点，可以将滚动轴承振动信号进行SDP变换，然后从图像处理的角度提取出反映花瓣形状的特征，采用相应的模式识别方法，以达到故障诊断目的。然而提出的特征中往往包含有冗余信息，影响故障诊断的精度，因此有必要采用维数约简算法对特征进行二次提取。线性局部切空间排列[9](Liner Local Tangent Space Alignment，LLTSA)作为一种新型流行学习算法，相比于局部保持投影[10](Locality Preserving Projection，LPP)等算法具有更好的降维效果[11]，能够充分挖掘高维非线性数据中的低维特征，具有很好的非线性复杂信息处理能力。

基于以上分析，本文提出了一种基于图像形状特征和LLTSA的滚动轴承故障诊断方法。即对滚动轴承振动信号进行SDP变换，然后从SDP图像中提取形状特征并采用LLTSA进行维数约简，最后将提取的低维特征输入支持向量机(Support Vector Machine，SVM)进行分类识别。滚动轴承的故障诊断实例验证了该方法的有效性。

1SDP方法和图像形状特征

1.1SDP方法的基本原理

在信号的离散数据采样序列中，xn是在时刻n时的幅值，xn+l是时刻n+l时的幅值，通过SDP变换公式，可以将其变换到极坐标空间P(r(n),Θ(n),φ(n))中的点。图1[7]为SDP方法的基本原理图。图中r(n)为极坐标的半径；Θ(n)为极坐标逆时针沿初始线旋转的角度；φ(n)为极坐标顺时针沿初始线旋转的角度。这三个变量的具体计算公式如下：

(1)

(2)

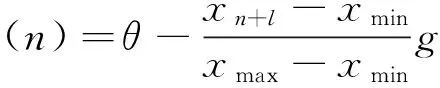
(3)

式中,xmin为采样序列的最小值；xmax为采样序列最大值；θ为镜像对称平面旋转角；g为角度放大因子；l为时间间隔参数。

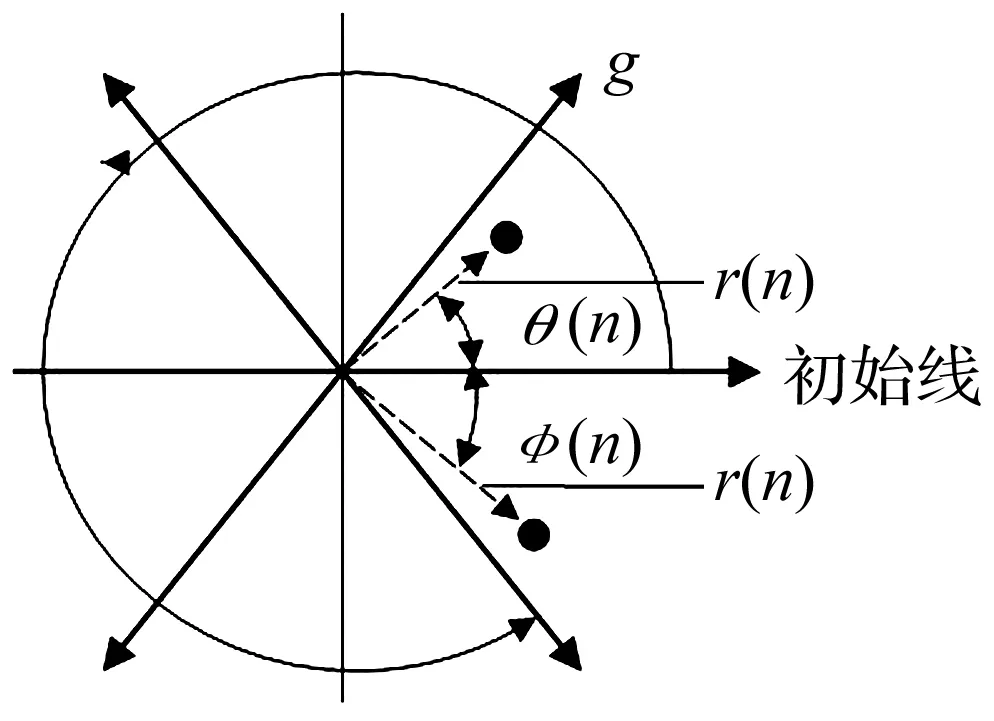
图1　SDP方法原理图Fig.1 Principle of SDP method

1.2SDP的性质及参数选择

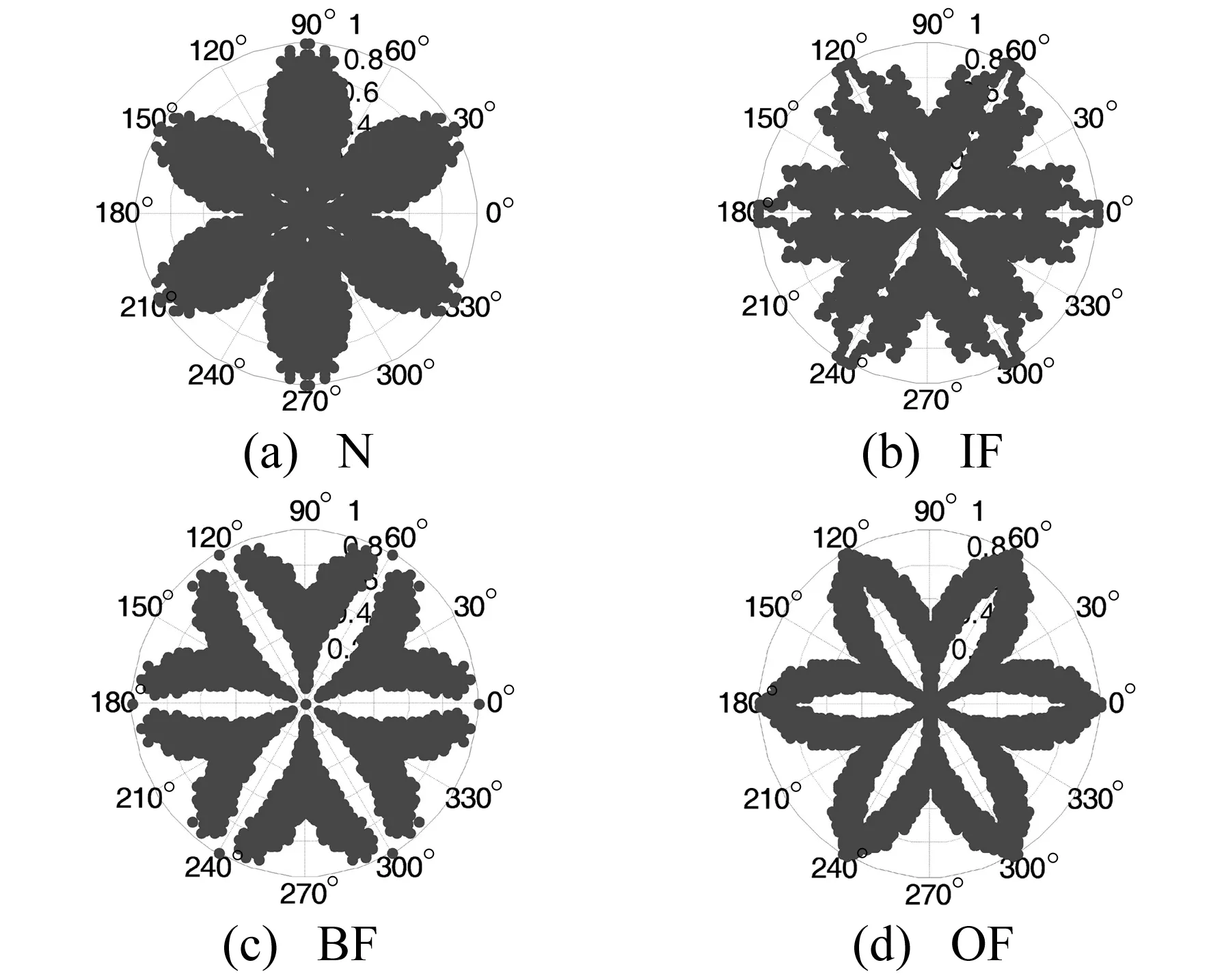
从SDP的计算公式可以看出，SDP方法的重点就在于极坐标中点位置的确定。在极坐标空间中，时域信号两个时间间隔为l的幅值决定了点的位置，假定l=1，如果信号中主要包含高频成分，则时域波形中i处幅值xi和i+1处幅值xi+1的差异就较大，而由SDP得到的极坐标空间中的点就会有较小的偏转角度和较大的半径，反之亦然[12]。因此，信号频率间的差异主要体现在极坐标中点分布位置和曲率的不同。图2为3个频率分别为100 Hz、200 Hz和400 Hz的正弦仿真信号以及高斯白噪声信号的SDP图像(θ=60°，g=40°，l=5)。从中可以看出，随着频率的增大，SDP图像的点的位置发生了较大变化，使得由点连接成的花瓣逐渐变得饱满，重叠部分也开始增加，SDP图像点的分布位置直观反映了正弦信号频率的变化。对比正弦信号和高斯白噪声信号的SDP图像可知，从周期信号到非线性信号的变化同样可以通过SDP图像的差异得到体现。

图2　仿真信号SDP图像Fig.2 SDP image of simulation signals

在SDP方法中，θ,g,l这三个参数的选择尤为重要。通常选取θ=60°，其镜像对称平面为0°、60°、120°、180°、240°、300°。在极坐标中，这六个平面组成雪花状的六边形。如果镜像对称平面旋转角θ过大，在极坐标中显示的图像不发生重叠，图像对称性较差；θ过小则图像的重叠较多，导致特征不明显。当θ为60°时，能够对信号特征清晰描述，便于特征的提取。通过大量实验发现[8]，不同信号之间的细微区别主要依靠g和l的选取，一般g要小于θ，取20°～50°为宜，l的值在1～10的范围内最佳。

1.3图像形状特征参数

图像的特征识别大致可归纳为三类[13]：颜色或灰度的统计特征；纹理、边缘特征；形状特征。由于不同信号SDP图像的差异主要体现在几何形状的不同上，因此采用形状特征对SDP图像进行描述。图像形状特征主要包括区域面积、区域边界、区域质心、与区域具有相同二阶中心矩的椭圆、方向角等参数，图3为以上各参数的示意图。上述几种形状特征参数定义如下[14]：

(1) 区域面积：描述了区域的大小，计算区域面积的一种简单方法就是对所属区域的像素进行计算。图3(a)中图像区域由5个白色像素点组成，按定义可知其区域面积为5像素。

(2) 区域质心：根据区域内所有点计算出来的坐标就是质心的坐标。图3(a)中灰色圆点即为白色像素图像区域质心。质心坐标的计算公式如下：

(4)

式中A为区域面积。

(3) 区域边界：是指包含图像区域最小的外接矩形，图3(a)中白色矩形为白色像素图像的区域边界。矩形的大小由矩形左上角顶点坐标以及矩形的长和宽决定。

(4) 与区域具有相同二阶中心矩的椭圆：图3(b)中椭圆即为与白色像素区域具有相同二阶中心矩的椭圆；图3(c)中长直线为椭圆长轴，短直线为椭圆短轴，长直线上两个红点为椭圆的焦点。

(5) 方向角：是指椭圆长轴与水平线的夹角。图3(c)中长直线与水平虚线的夹角即为方向角。

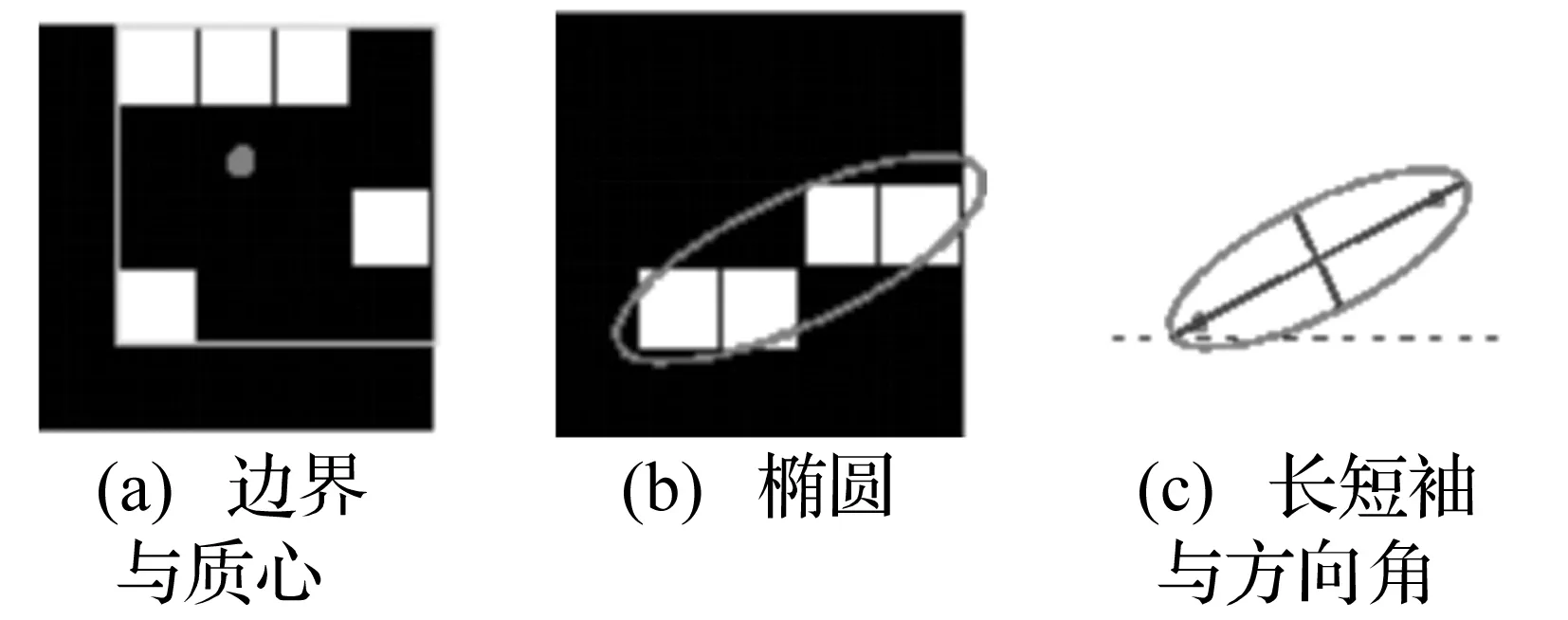
图3　形状特征参数示意图Fig.3 Sketch map of shape feature

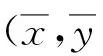
2线性局部切空间排列

线性局部切空间排列的主要思想就是寻找一个转换矩阵A将RD空间中具有N个点的含噪数据集XORG(即本文中的故障样本集)映射为Rd空间数据集Y=[y1,…,yN]，即：

Y=ATXORGHN(d

(5)

式中HN=I-eeT/N为中心矩阵，I为单位矩阵，e为所有元素为1的N维列向量。Y为XORG潜在的d维非线性流行。

LLTSA主要有以下几个步骤[15]：

(1) 主成分分析投影。使用PCA将数据集映射到主体子空间，用APCA表示PCA的转换矩阵，同时为了表示方便，仍采用X表示PCA子空间数据集。

(2) 确定领域。采用K-近邻法(KNN)搜索数据点xi的领域，即首先采用欧式距离构造所有数据点的距离矩阵，然后通过分析距离矩阵找到数据点xi的k个同类近似点xj。

(3) 获取局部信息。计算由XiHk(Xi=[xi1,…,xik])的d个最大特征值对应d个特征矢量构成的矩阵Vi。其中Hk=I-eeT/k。

(4) 构造排列矩阵。通过局部累加构造矩阵B为：

B(Ii,Ii)←B(Ii,Ii)+WiWiT

(i=1,2,…,N)

(6)

初始化B=0，式中Ii={ii,…,ik}表示xi的k个近邻点的索引集，Wi=Hk(i-ViViT)(i=1,2,…,N)。

(5) 计算映射。计算广义特征问题的特征值和特征矢量：

XHNBHNXTα=λXHNXTα

(7)

与特征值λ1,λ2,…,λn(λ1<λ2…<λn)对应的特征矢量解为α1,α2,…,αd，则ALLTSA=(α1,α2,…,αd)，因此转换矩阵A=APCA×ALLTSA，X→Y=ATXORGHN。

3形状特征-LLTSA-SVM轴承故障诊断方法

滚动轴承发生不同故障后，故障信号中会出现不同频率成分的周期性冲击，使得信号的幅值和频率成分发生改变，进而影响极坐标空间中点的分布情况。而前面定义的形状特征又主要由点的分布情况决定，点分散的越开，重叠的点越少，则区域面积和区域边界就会变大，使得区域质心位置和椭圆位置发生改变，而方向角也会随着椭圆位置的改变而变化，反之亦然。因此，滚动轴承振动信号中频率成分的改变引起的点分布位置的变化，就建立了轴承振动信号与形状特征之间的一种内在联系，使得从振动信号SDP图像中提取的形状特征能够对轴承振动信号进行表征。同时，LLTSA具有较强的非线性信息处理能力，通过它对形状特征进行维数约减，能够剔除形状特征中的冗余信息，可以获得一个维数低、敏感度高且聚类效果好的低维特征。另一方面，支持向量机(SVM)是建立在统计学基础上的机器学习方法，具有小样本学习、泛化能力强等优点，是目前故障诊断领域比较常用的方法[2, 16]。因此，把SVM作为诊断方法的一部分，将其用于低维特征的分类识别，以达到故障诊断的目的。

基于图像形状特征-LLTSA-SVM的滚动轴承故障诊断方法的流程如图4所示，具体步骤如下：

图4　形状特征和LLTSA轴承故障诊断方法流程图Fig.4 Flow chart ofbearing fault diagnosis smethod based image shape feature and LLTSA

(1) 对滚动轴承故障信号首先进行降噪处理，以突出故障信号的特征和提高信噪比，然后对降噪后信号进行SDP变换，得到SDP雪花图像。进行SDP变换时，采用图像相关分析确定g和l的取值，即g在20°～50°的范围内步长为10°，l在1～10的范围内步长为1，分别固定g和l的值，由于需要将不同故障状态进行区分，因此将各故障状态的雪花图进行两两相关分析，取各相关系数之和最小时对应的g和l作为最优值。图像相关性的计算公式为：

(2) 根据前面定义的图像形状特征，对各SDP图像进行特征提取，得到一个维数为11的图像形状特征集。

(3) 将训练样本和测试样本特征集同时输入LLTSA进行训练，求得转换矩阵。

(4) 对训练样本和测试样本进行维数约简，分别得到d维的非线性主流行(即经过约简的特征集)，其中1≤d≤11。

(5) 将约简后的训练样本输入SVM中进行训练，而后将约简后的测试样本输入训练好的SVM中进行测试，得到诊断结果。

4实验验证与结果分析

本文采用美国CWRU(Case Western Reserve University)轴承数据中心网站的滚动轴承故障数据来验证本文所提方法的有效性。测试轴承为深沟球轴承，轴承型号为SKF6205，轴承损伤是通过电火花加工技术人为设置，并通过加速度传感器采集振动信号。实验中，实验转速为1 797 r/min，载荷为0，故障损伤直径为0.177 8 mm，采样频率为12 kHz，对于轴承正常(N)、内圈故障(IF)、滚动体故障(BF)和外圈故障(OF)4种状态，每种状态测取20组数据样本。通过多次实验发现，数据样本点数为4 096时，得到的图像离散点少且花瓣饱满，故样本长度确定为4 096。

采用SDP方法对时域信号进行变换，利用图像相关分析确定g和l的取值，通过计算，发现g=40°以及l=2时得到相关系数之和最小。图5为轴承4种状态在最优g和l值下的SDP图像，从中可以看出，轴承4种状态的SDP图像具有明显的差异，通过肉眼就可以直观地分辨出轴承的状态。通过对大量实验数据的分析，发现轴承4种状态的SDP图像具有很好的重复性。

图5　轴承4种状态的SDP图像Fig.5 SDP image of bearing with four kinds of fault

由于SDP图像是通过对称镜像得到，取其中一部分花瓣进行分析就能够表达整个图像的特点。因此，选择第一象限两个花瓣进行分析。首先，只绘制第一象限两个花瓣的极坐标图并将其直接转换为二值图像，如图6所示。然后，通过Matlab中regionprops函数实现对轴承4种状态第一象限花瓣形状特征的提取，能够得到4个20×11的特征矩阵。因为二值图像是由第一象限花瓣极坐标图直接转换得到，极坐标中心与二值图像左下角的相对位置不会变化，而regionprops函数默认二值图像左下角为0像素点，使得形状特征的计算基准是一致的，这就保证了轴承不同故障状态形状特征的可比性。表1给出了轴承4种状态下2个样本信号的11维形状特征。

图6　第一象限花瓣二值图像Fig.6 Binary image of petals in first quadrant

在得到形状特征后，通过LLTSA将11维的特征向量进行维数约简。设置邻域参数K=12，目标维数d=3。作为比较，采用同样参数设置的LTSA(局部切空间排列)和LPP对特征集进行降维处理。图7为3种降维方法低维特征提取效果图。从图7中可以看出，LLTSA提取的低维特征能够将轴承的4种状态完全区分开，并且低维特征具有较好的聚类效果；LTSA虽然基本上能将4种状态区分开，但仍然有少部分滚动体故障样本混入到外圈故障和内圈故障样本中，并且不同故障类型的距离也较近；LPP能够将正常和外圈故障进行分离，并且各状态的聚类效果较好，但也有部分内圈故障样本和部分滚动体故障样本出现了的混叠。以上分析表明LLTSA的性能要优于LTSA和LPP。

表1　轴承4种状态下的形状特征

图7　3种流行学习算法特征约简结果对比Fig.7 Comparison of dimension reduction effects of three manifold algorithms

为了进一步说明本文方法的有效性，采用SVM对提取低维特征进行分类识别。作为比较，同样采用SVM对未经约简的原始特征、经LTSA约简的低维特征以及经LPP约简的低维特征进行分类识别。实验将各状态20组样本随机分成两组，10组作为训练样本，剩余10组作为测试样本。试验中SVM的核函数选用效果较优的径向基核函数(RBF)，惩罚参数C=10，核参数g=1，轴承正常、内圈故障、滚动体故障以及外圈故障的训练标签依次为1、2、3和4。表2为各方法故障特征的识别结果。

表2　支持向量机识别结果/%

从表2可以看出，根据SDP图像提取的形状特征虽然能够较为准确的诊断出轴承的工作状态，但识别率不是很高，这说明提取的形状特征中含有一些重叠的故障信息，降低了故障分类的准确率，从而证明需要进行维数约简以提取低维特征。而LTSA-SVM的识别率相比于不进行维数约简的识别率有了提高，但和图7(b)的分析结果一样，除轴承正常状态被完全正确识别外，其余三种状态都有错误识别。在LPP-SVM中，有2个滚动体故障被错分为内圈故障，识别率得到了一定程度的提高。在LLTSA-SVM中，轴承各状态的识别率均达到了100%，效果优于LPP-SVM和LTSA-SVM方法，这说明本文所提方法是有效可行的。

5结论

本文在SDP方法、图像处理和LLTSA的基础上提出了基于图像形状特征和LLTSA的滚动轴承故障诊断方法。结合SDP对不同信号的可视化能力、形状特征对图像的表征能力以及LLTSA对非线性特征的提取能力等特点，对滚动轴承进行故障诊断。实验结果表明，提取的SDP图像形状特征能够反映轴承状态的变化，而经LLTSA维数约简后的低维特征聚类效果更好，提高了故障特征的分辨率，简化了特征数据，增强了故障模式识别的准确率。将提取后的低维特征输入SVM进行识别，对轴承4种状态的识别率均达到了100%，验证了本文方法的有效性。

参 考 文 献

[1] Li Xu,Zheng A’nan,Zhang Xu-nan,et al. Rolling element bearing fault detection using support vector machine with improved ant colony optimization[J]. Measurement,2013,46:2726-2734.

[2] 唐贵基,邓飞跃,何玉灵,等. 基于时间-小波能谱熵的滚动轴承故障诊断研究[J]. 振动与冲击,2014,33(7):68-72,91.

TANG Gui-ji,DENG Fei-yue,HE Yu-ling,et al. Rolling element bearing fault diagnosis based on time-wavelat energy spectrum entropy[J]. Journal of Vibration and Shock,2014,33(7):68-72,91.

[3] 程利军,张英堂,李志宁,等. 基于时频分析及阶比跟踪的曲轴轴承故障诊断研究[J]. 振动与冲击,2012,31(19):73-78.

CHENG Li-jun,ZHANG Ying-tang,LI Zhi-ning,et al.Fault diagnosis of an engine’s main bearing based on time-frequency analysis and order tracking[J]. Journal of Vibration and Shock,2012,31(19):73-78.

[4] 窦唯,刘占生. 旋转机械故障诊断的图形识别方法研究[J]. 振动与冲击,2012,31(17):171-175.

DOU Wei,LIU Zhan-sheng. A fault diagnosis method based on graphic recognition for rotating machine[J]. Journal of Vibration and Shock,2012,31(17):171-175.

[5] 张立国,杨瑾,李晶,等. 基于小波包和数学形态学结合的图像特征提取方法[J]. 仪器仪表学报,2010,31(10):2285-2290.

ZHANG Li-guo,YANG Jin,LI Jing,et al. Image characteristic extraction method based on wavelat packet andmathematicalm orphology[J]. Chinese Journal of Scientific Instrument,2010,31(10):2285-2290.

[6] Shibata K,Takahashi A,Shirai T. Fault diagnosis of rotating machinery through visualization of sound signals[J]. Mechanical Systems and Signal Processing,2000,14(2):229-241.

[7] Wu Jian-da,Chuang Chao-qin. Fault diagnosis of internal combustion engines using visual dot patterns of acoustic and vibration signals[J]. NDT Int．,2005,38(8):605-614.

[8] Delvecchio S,D’Elia G,Mucchi E,et al. Advanced signal processing tools for the vibratory surveillance of assembly faults in diesel engine cold tests[J]. ASME Journal of Vibration and Acoustics,2010,132:1-10.

[9] Kouropteva O,Okun O,Pietikainen M. Supervised locally linear embedding algorithm for pattern recognition[J]. Pattern Recognition and Image Analysis,2003,2652(9):386-394.

[10] He X F,Yan S C,Hu Y X,et al. Face recognition using laplacianfaces[J]. IEEE Trans．Pattern Analysis and Machine Intelligence,2005,27(3):328-340.

[11] Zhang T H,Yang J,Zhao D L,et al. Linear local tangent space alignment and application to face recognition[J]. Neurocomputing,2007,70:1547-1553.

[12] 杨成,冯焘,王中方,等. 基于SDP法诊断发动机的异响[J]. 声学技术,2010,29(5):523-527.

YANG Cheng,FENG Tao,WANG Zhong-fang,et al. Abnormal noise diagnosis of motorcycle engines based on Symmetrized Dot Pattern method[J]. Technical Acoustics,2010,29(5):523-527.

[13] 任玲辉,刘凯,张海燕. 基于图像处理技术的机械故障诊断研究进展[J]. 机械设计与研究,2011,27(5):21-24.

REN Ling-hui,LIU Kai,ZHANG Hai-yan. Progress on mechanical fault diagnosis based on image processing[J]. Machine Design and Research,2011,27(5):21-24.

[14] 秦襄培,郑贤中. Matlab数字图像处理宝典[M]. 北京:电子工业出版社,2011.

[15] 李锋,汤宝平,陈法法. 基于线性局部切空间排列维数化简的故障诊断[J]. 振动与冲击,2012,31(13):36-40.

LI Feng,TANG Bao-ping,CHEN Fa-fa. Fault diagnosis model based on dimension reduction using linear local tangent space alignment[J]. Journal of Vibration and Shock,2012,31(13):36-40.

[16] 向丹,葛爽. 一种基于小波包样本熵和流行学习的故障特征提取模型[J]. 振动与冲击,2014,33(11):1-5.

XIANG Dan,GE Shuang. A model of fault feature extraction based on wavelet packet sample entropy and manifold learning[J]. Journal of Vibration and Shock,2014,33(11):1-5.

Fault diagnosis method based on image shape features and LLTSA

ZHANG Qian-tu1,2, FANG Li-qing2

(1. Military Representative Office in NO.356 Factory, Kunming 650114, China;2. Department of Artillery Engineering, Ordnance Engineering College, Shijiazhuang 050003, China)

Abstract:Aiming at fault diagnosis problems of rolling bearing, a fault diagnosis method based on image shape features and linear local tangent space alignment (LLTSA) was proposed. Firstly, a time waveform was transformed into a snowflake image in polar coordinate space with the symmetrized dot pattern (SDP) method. The image shape features were initially extracted on the basis of analyzing the characteristics of the image. Secondly, LLTSA was introduced to compress the initial high-dimensional features into low-dimensional ones with a better discrimination. Finally, a support vector machine (SVM) was employed to classify and evaluate low-dimensional features. The test results of rolling bearing fault diagnosis showed that the image shape features can characterize bearing states, and LLTSA can reduce the complexity of feature data and enhance their clustering effect; furthermore, a relatively higher identification rate of four bearing states reaches 100% with SVM, the effectiveness of the proposed method was verified.

Key words:symmetrized dot pattern (SDP); shape feature; linear local tangent space alignment (LLTSA); support vector machine (SVM); fault diagnosis

基金项目：军内科研项目

收稿日期：2015-01-07修改稿收到日期：2015-05-03

通信作者房立清 男，博士后,博士生导师，1969年生

中图分类号:TH165.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.028

第一作者 张前图 男，硕士生，1991年生