基于响应灵敏度分析的桥梁结构损伤和车辆参数的识别

张春丽， 吕中荣

(1.重庆建筑工程职业学院,重庆　400072； 2. 中山大学 力学系,广州　510275)

基于响应灵敏度分析的桥梁结构损伤和车辆参数的识别

张春丽1， 吕中荣2

(1.重庆建筑工程职业学院,重庆400072； 2. 中山大学 力学系,广州510275)

摘要：基于响应灵敏度分析利用车-桥耦合系统的加速度响应进行桥梁结构的局部损伤和车辆参数识别。在正问题中建立了连续桥梁结构和车辆耦合系统的有限元模型，利用Newmark 直接积分法求出在移动车载作用下系统的动态响应，并进一步推导出动态响应对系统物理参数的时域响应灵敏度。在反问题中利用该响应灵敏度矩阵进行系统的有限元模型修正，识别出桥梁的局部损伤和车辆参数，讨论了人工噪声对识别结果的影响。算例表明该方法具有精度高、对测量噪声不敏感等特点。

关键词：车-桥耦合；损伤识别；响应灵敏度；模型修正

桥梁结构损伤识别是近年来土木工程领域的研究热点。由于基于振动的结构损伤识别法具有非破坏性、方便、快速和廉价的优点，该方法具有广阔的工程应用前景。一般地讲，由于局部损伤的产生，在该区域的结构刚度和承载能力将会有所下降，而结构的质量特性一般不会受到影响， 结构的模态参数( 模态频率、振型、阻尼等) 也将随之而改变。通过研究结构的振动特性来识别结构是否发生损伤，并确定损伤的位置和程度。

基于结构振动响应和系统动态特性参数的结构损伤检测方法经过近几十年的发展，已取得了一些有成效的研究成果。常用的基于振动的结构损伤频域方法主要包括：基于模态频率[1]和振型[2]方法，基于柔度的方法[3]，基于曲率的方法[4]， 基于应变模态的方法[5]，基于模态应变能的方法[6]。在时域内，Cattarius等[7]研究了一种利用时域上的振动响应数据来识别智能结构上存在的损伤的方法。Lu等[8]提出了一种基于响应灵敏度的损伤识别方法。随着数学和计算机的发展，为结构损伤识别提供了一些新方法，如基于神经网络的识别方法[9]，基于模糊逻辑和遗传算法的识别方法[10]，以及基于小波变换的方法[11]等。

对于大型桥梁结构，难以利用人工激振的办法来获得桥梁的强迫振动响应，车桥耦合系统的振动响应分析以及利用车桥耦合系统响应进行损伤识别成为近年来的研究热点[12-16]。在利用车桥耦合系统响应的损伤识别中，往往假定车辆参数是已知的。更一般情况下，车辆的参数也是未知的。因此本文进行桥梁损伤识别时，将车辆的物理参数识别也看作是未知参数进行识别。以三跨连续梁为算例，对多个局部损伤工况进行了识别，并进一步讨论了测量噪声和测量时间对识别结果的影响。仿真算例结果表明本文方法仅利用少量几个测点的加速度响应就能成功同时识别桥梁损伤和车辆的物理参数。

1正问题：车桥耦合系统有限元模型

1.1车-桥耦合系统的运动方程

移动车载作用下的车-桥耦合系统模型如图1所示，系统的强迫振动有限元方程可以写成如下形式

(1)

式中，Mb，Kb分别为梁的整体质量矩阵和刚度矩阵，阻尼矩阵Cb仍采用Rayleigh阻尼模型。Pint为梁和车载的相互作用力，Hc为荷载作用矩阵，除了荷载作用的单元两个节点的所有自由度为1之外，矩阵的其它元素都为零。

图1　车桥耦合系统模型Fig.1 Sketch of the coupled bridge-vehicle system

将车辆模拟为两自由度组成的五参数模型。mv1、mv2为上下两部分物体的质量，cv为悬簧的阻尼，kv1、kv2分别为悬簧的刚度以及轮胎的刚度。车桥耦合系统的运动方程可以表示为[13]

(2)

其中：

对车-桥耦合系统振动方程(2)，采用Newmark直接积分法进行求解获得系统的振动响应。

1.2响应对损伤参数灵敏度及系统参数的识别

式(2)对系统的第i个单元抗弯刚度(EI)i求偏导数，有

(3)

式(2)两边分别对车辆质量、弹簧和阻尼参数求导得

(4)

(5)

(6)

其中

响应对车辆的参数灵敏度可以由式(4)～(6)利用直接积分法计算求得。

2反问题：桥梁损伤和车辆参数的同时识别

识别问题可表述达：寻找物理参数EI和车辆参数，也就是α=[EI1,EI2,…,EIN,mv1,mv2,kv1,kv2,cv]T=[[PEI],[Pv]]T使得计算出来的响应，如加速度或应变与测量的相应响应最好地匹配:

(7)

(8)

识别过程分为以下两步:

1)识别车辆参数

利用式(8)，可由下式获得车辆参数的增量

(9)

式 (9)的解由阻尼最小二乘法求得[17]

{δPv}=([Sv]T[Sv]+λI)-1[Sv]T{δR}

(10)

式中,λ为正则化参数，本文使用L-曲线[18]法寻找最优阻尼因子λ。当λ趋近于0的时候，ΔEj就接近由最小二乘法计算出来的结果。L-曲线法的计算方法可详细查阅文献[19]。更新后的车辆参数为

{Pv}={Pv}0+{δPv}

(11)

2)损伤识别

车参数更新后，类似第利用式(11)可得到桥梁抗弯刚度参数的识别方程式

{δR}=[SEI]{δPEI}

(12)

利用阻尼最小二乘法求得抗弯刚度参数的增量

{δPEI}=([SEI]T[SEI]+λI)-1[SEI]T{δR}

(13)

进一步可得更新后的抗弯刚度参数

{PEI}={PEI)}0+{δPEI}

(14)

3数值算例

取图1所示的三跨简支梁桥作为算例，桥的物理参数为: 杨氏模量E=3.3×1010Pa, 密度ρ=2.5×103kg/m3, 宽度为1 m,高度为0.6 m 每跨长度为10 m, 车的参数为mv1=3.6×103kg,mv2=0.25×103kg,cv=1.0×103Ns/m,kv1=6.0×105N/m,kv2=8.5×105N/m。为减少计算时间,在有限元模型中只将每跨离散为8个梁单元，三跨共24个单元。若采用更精细的有限单元，将导致计算时间会大大增加，对损伤和参数识别的精确程度也略有影响。无损伤时桥梁的前6阶频率分别为 9.885, 12.668, 18.498, 39.549, 45.076, 55.311 Hz。在计算阻尼矩阵时只用了前两阶低阶的模态阻尼比，并人为简单地将其假设为0.01。对于数值仿真计算，阻尼比取何值对识别结果影响不大。在实际工程中，模态阻尼比可从模态测试结果获得。

3.1无噪声时多损伤识别

为模拟多处损伤，假设在第1号、8号、14号、17号和23号单元分别有15%、5%、8%、10%和10%的抗弯刚度的减损。这里选取的1号、8号、17号单元紧邻各跨支座、23号也靠近支座，一般来说这些支座附近单元的损伤一般难以准确识别，笔者特选取了这些单元进行损伤识别以显示本文方法的有效性。第二跨中选了跨中附近的14号单元作为损伤单元，损伤程度取为8%，以表示其与别的单元不同的损伤程度。假定车辆以10 m/s 的速度通过桥梁，计算响应时的时间步长为0.002 s. 车辆的初始参数分别取为2 000 kg 、200 kg、500 Ns/m、 3.0×105N/m、4.0×105N/m。 5个加速度计A1-A5 用于损伤和参数识别，如图1所示，A1位于第一跨的L/4 位置，A2位于第二跨的L/2位置， A3 和A4位于第三跨的 L/4 和3L/4位置，A5 位于车的上部质量处。车辆参数识别的结果见表1，可以看出识别的车辆参数和车辆的真实非常接近，说明识别的结果是正确的。桥梁损伤识别结果如图2所示，在第1号单元出现最大识别误差为 -0.5% 。该算例表明本文方法是正确和有效的。

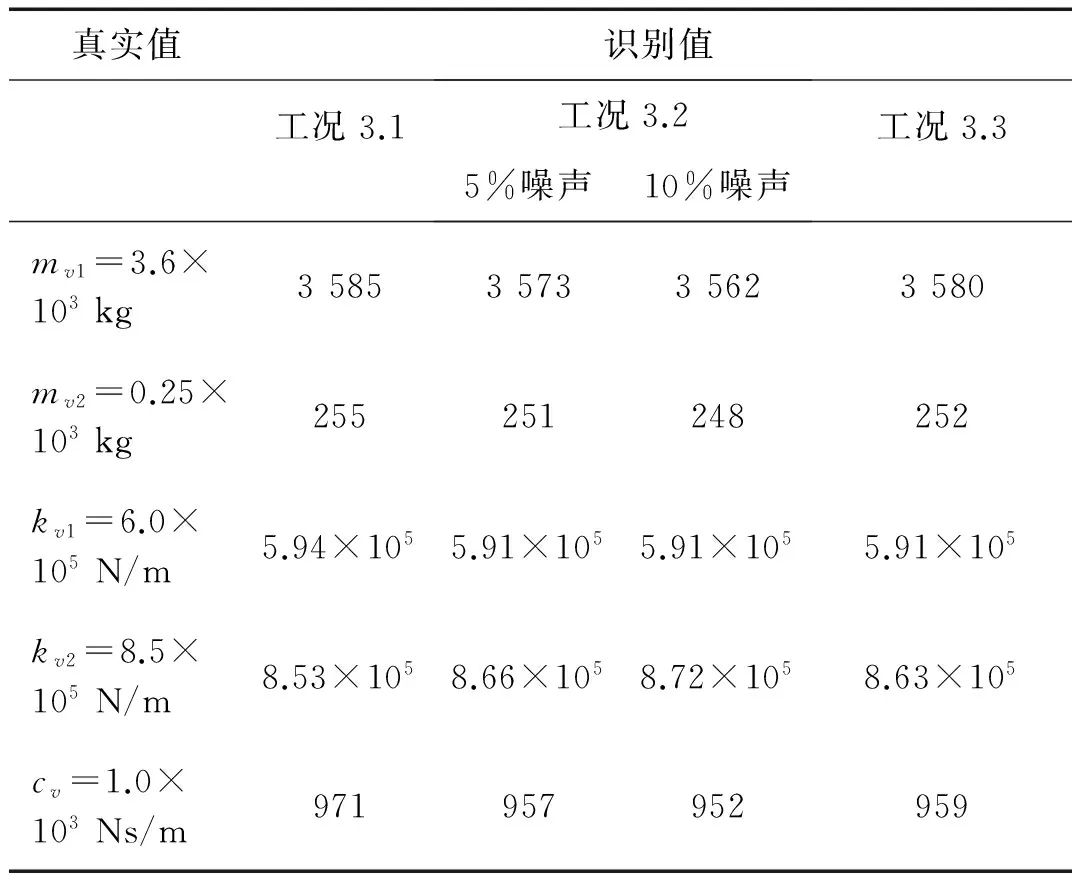
表1　不同工况下车辆参数的识别结果

图2　无噪声时多损伤识别结果Fig.2 Results of multiple damage identification(without noise)

3.2有噪声时多损伤识别

为模拟真实测量响应的噪声，在计算加速度响应中增加零均值和标准差为单位1的正态分布的随机噪声

(15)

图3　不同噪声时多损伤识别结果Fig.3 Results of multiple damage identification under different noise level

3.3不同测量时间的影响

本工况研究不同测量时间长短对识别结果的影响。假设车的行驶速度为5 m/s, 这样车辆通过桥梁的时间为6 s，也就是测量的持续时间为6 s。考虑5% 的噪声水平并和上面工况的结果对比。图4给出了不同测量时间下桥梁识别的结果的对比。6 s 测量时间对应的最大识别误差为1号单元的-0.97%，而3s测量时间对应的最大识别误差为1号单元的-2.5%。车辆参数的识别结果见表1所列，可以看出识别的车辆参数和车辆的真实非常接近，说明识别的结果是正确的。 本工况表明，增加测量时间可以提高识别的精度。

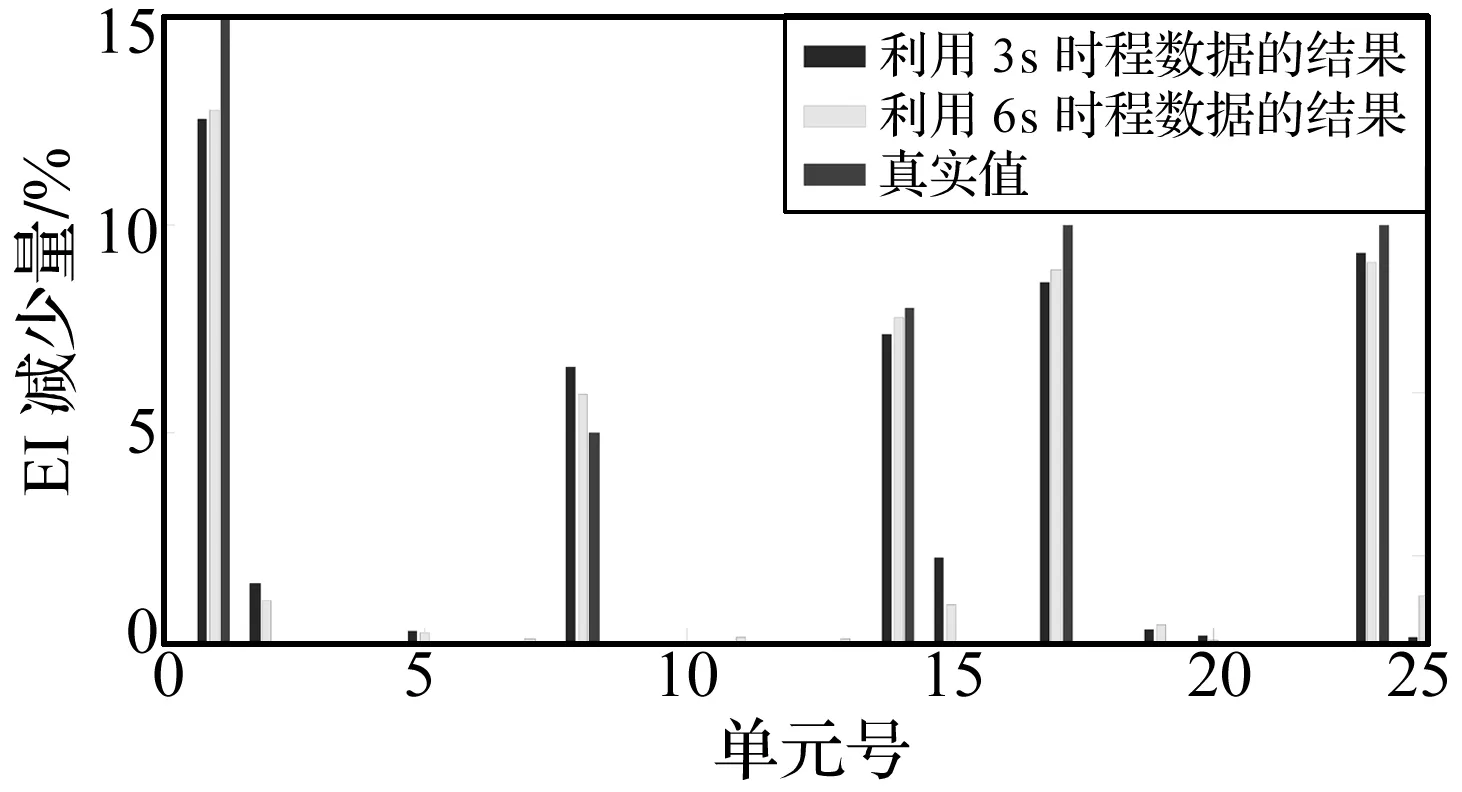
图4　不同测量时间下识别结果的比较Fig.4 Comparison on damage identification results for different time duration

4结论

本文提出了一种基于响应灵敏度分析的有限元模型修正法进行桥梁损伤和车辆参数的同时识别。该方法仅需要利用少量几个测点的加速度响应就能得到精度较高的识别结果。同时算例表明本文方法对模拟的人工测量噪声不敏感，在10%的噪声水平下仍能获得满意的结果。同时增加测量的时间，利用更多的加速度响应数据可以进一步提高识别的精度。本文车辆采用的是5自由度的简单模型，这与实际车辆有较大差别，因此建立复杂车辆模型的车-桥耦合系统并进行车辆参数识别和桥梁的损伤识别是后续研究的内容。

参 考 文 献

[1] Cawley P, Adams R D. The location of defects in structures from measurements of natural frequencies[J]. Journal of Strain Analysis,1979,14(2):49-57.

[2] Shi Z Y,Law S S,Zhang L M. Damage localization by directly using incomplete mode shapes[J]. Journal of Engineering Mechanics,2000,126(6):656-660.

[3] Pandy A K ,Biswas M. Damage detection in structures using changes in flexibility[J]. Journal of Sound and Vibration,1994,169(1):3-17.

[4] Wahab M M A,Roeck G D. Damage detection in bridges using modal curvatures:application to real damage scenario[J]. Journal of Sound and Vibration,1999,226(2):217-235.

[5] Shi Z Y,Law S S,Zhang L M. Structural damage localization from modal strain energy change[J]. Journal of Sound and Vibration,1998,218(5):825-844.

[6] Liu X,Lieven N A J, Escamilla-Ambrosio P J. Frequency response function shape-based methods for structural damage localization[J]. Mechanical Systems and Signal Processing,2009,23(4):1243-1259.

[7] Cattarius J,Inman D J. Time domain analysis for damage detection in smart structures[J]. Mechanical Systems and Signal Processing,1997,11(3):409-423.

[8] Lu Z R,Law S S. Features of dynamic response sensitivity and its application in damage detection[J]. Journal of Sound and vibration,2007,303(1/2):305-329.

[9] 孙宗光,高赞明,倪一清. 基于神经网络的桥梁损伤位置识别[J]. 工程力学,2004,21(1):43-47.

SUN Zong-guang,GAO Zan-ming,NI Yi-qing. Identification of damage location in bridge deck by Neural Network[J]. Engineering Mechanics,2004,21(1):43-47.

[10] 冯柯,崔永固,李静,等. 基于模糊逻辑和遗传算法的工程机械故障诊断[J]. 解放军理工学院学报:自然科学版,2005,8(4):385-389.

FENG Ke,CUI Yong-gu,LI Jing,et al. Fault diagnosis based on fuzzy logic and genetic algorithms of engineering machine[J]. Journal of PLA University of Science and Technology,2005,8(4):385-389.

[11] Law S S,Li X Y,Lu Z R. Structural damage detection from wavelet coefficient sensitivity with model errors[J]. Journal of Engineering Mechanics,2006,132(10):1077-1087.

[12] Law S S,Wu S Q. Evaluating the response statistics of an uncertain bridge-vehicle system[J]. Mechanical Systems and Signal Processing,2012,27:576-589.

[13] 王文洁,吕中荣,刘济科. 含呼吸裂缝的桥梁振动响应与时频特性分析[J]. 振动与冲击,2013,32(11):12-16.

WANG Wen-jie,LÜ Zhong-rong,LIU Ji-ke. Dynamic response and time-frequency feature analysis for a bridge with breathing cracks[J]. Journal of Vibration and Shock,2013,32(11):12-16.

[14] Jaksic V,Connor A O,Pakrashi V. Damage detection and calibration from beam-moving oscillator interaction employing surface roughness[J]. Journal of Sound and Vibration,2014,333(17):3917-3930.

[15] 陈代海,陈淮,李整,等. 形函数时变性对汽车公路梁桥竖向耦合振动影响分析[J]. 振动与冲击,2014,33(14):20-24.

CHEN Dai-hai,CHEN Huai,LI Zheng,et al.Effect of time variability of element interpolation function on vehicle-bridge vertical coupling vibration of highway beam bridges[J]. Journal of Vibration and Shock,2014,33(14):20-24.

[16] Zhong H,Yang M J,Gao Z L.Dynamic responses of prestressed bridge and vehicle through bridge-vehicle interaction analysis[J]. Engineering Structures,2015,87:116-125.

[17] Tikhonov A M. On the solution of ill-posed problems and the method of regularization[J]. Soviet Mathematics,1963,4:1035-1038.

[18] Hansen P C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev 1992,34:561-580.

[19] Hansen P C. Rank-deficient and discrete ill-posed problems:numerical aspects of linear inversion. SIAM,Philadelphia,PA,1998.

Identification of a bridge’s structural damage and vehicular parameters based on dynamic response sensitivity analysis

ZHANG Chun-li1, LÜ Zhong-rong2

(1. Chongqing Jianzhu College, Chongqing 400072, China；2. Department of Applied Mechanics, Sun Yat-sen University, Guangzhou 510275, China)

Abstract:Here, both local damages in a bridge’s deck and parameters of moving vehicles were identified with a bridge-vehicle coupled system’s dynamic responses induced by vehicles moving on the top of the bridge deck. The local damage is simulated by a reduction in the elemental flexural rigidity of the beam. The dynamic model of the bridge-vehicle coupled system was established using the finite element method and the dynamic responses of the system were obtained using Newmark direct integration method. In the inverse analysis, a dynamic response sensitivity-based finite element model updating approach was used to identify both local damages of the bridge deck in element level and parameters of vehicles. The solution was obtained iteratively with the penalty function method and the regularization from the measured structural dynamic responses. A multi-span continuous beam was studied as an numerical example to illustrate the correctness and efficiency of the proposed method. The effects of measurement noise, and measurement time duration on the identification results were investigated. The results indicated that the proposed method is efficient and robust for both damage identification and vehicular parametric identification; good identified results can be obtained with time histories of several measurement points.

Key words:bridge-vehicle coupled system; damage identification; response sensitivity; model updating

基金项目：国家自然科学基金(11172333);重庆市教委科学技术研究项目(KJ1404104)

收稿日期：2015-03-20修改稿收到日期：2015-05-20

通信作者吕中荣 男，博士，教授,1975年3月生

中图分类号:TH212；TH213.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.027

第一作者 张春丽 女，硕士，副教授,1980年 4月生

E-mail:lvzhr@mail.sysu.edu.cn