基于橡胶刚度频散的隔振器阻抗研究

黄伍德, 陈光冶， 车驰东

(上海交通大学 船舶海洋与建筑工程学院, 上海　200240)

基于橡胶刚度频散的隔振器阻抗研究

黄伍德, 陈光冶， 车驰东

(上海交通大学 船舶海洋与建筑工程学院, 上海200240)

摘要：根据橡胶动模量和刚度的实验结果，拟合出隔振器刚度随频率的变化关系式，并通过隔振器的动、静刚度确定其待定系数。在传统四端参数法的计算中计入了刚度的频散效应，以提高橡胶隔振器阻抗计算的准确性。同时设计了一种基于纯加速度测量的阻抗测试方法并对两型隔振器进行了阻抗测试，由实测数据与不同刚度假设下的计算结果比较可见：计入刚度频散效应后的隔振器阻抗计算更精确，而基于加速度测量的阻抗测试是可行的。

关键词：隔振器；阻抗；刚度频散；加速度测量

随着现代船舶对动力性能要求的不断提高，动力机械所引起的振动问题日益突出。根据“最优的噪声与振动控制必须从源头出发”[1]的理念，各类金属弹簧和橡胶隔振设备被认为是最简单有效且经济合理的振动控制措施,而阻抗是描述隔振元件动态性能最主要的指标之一。

目前常见阻抗研究方法有理论分析、数值仿真和实验测量。潘孝勇等[2]建立了一种基于超弹性、分数导数和摩擦模型的橡胶隔振器动态特性的非线性模型以描述橡胶隔振器的动态特性，但该方法仅在低于100 Hz的低频段进行研究，对中、高频段没有涉及。赵广等[3]提出了一个基于动态激励实验的，由橡胶隔振器静态刚度、位移系数和频率系数组成的动态刚度模型对橡胶隔振器动态特性进行预测，但该模型未考虑橡胶的内阻尼和摩擦耗能，且只在低于100 Hz的频段内进行实验验证，高频范围内可行性未知。范宣华等[4]通过建立振动台、夹具和橡胶隔振试件整体有限元模型，对橡胶隔振试件振动台随机振动试验进行了仿真研究，并与实验结果对照对仿真进行改善。陈辉等[5]使用落锤式冲击机对BE120和EA120两型橡胶隔振器进行两个方向冲击载荷同时作用下的冲击试验研究以探究多方向冲击对隔振器冲击特性的影响。计方等[6]基于四端参数法分析了计及高频波动效应的圆柱型橡胶隔振器的阻抗特性，以E型和BE型隔振器为研究对象，借助有限元软件数值计算隔振器的机械阻抗。

橡胶隔振器是舰船上常用的隔振装置，在传统阻抗计算或数值仿真中，常将其刚度设为定值，通常取其静刚度或固有频率下的动刚度。但实际橡胶等高分子黏弹性材料的杨氏模量是频散(随振动频率变化)的，且隔振器的刚度又正比于其材料的杨氏模量，故基于定刚度的阻抗计算往往与实测结果有一定偏差。

另一方面，传统的阻抗测试常采用力传感器，而力传感器安装复杂，且其有效频响会受到负载的较大影响。即使是进口的力传感器也只能保证1 kHz的有效测量范围。因此相关ISO[7]及国标[8-9]中均建议慎用力传感器，并明确严格地规定了力传感器的频响要求及标定方法。而加速度传感器不仅安装方便，且一般比力传感器有更大的有效频响范围，一般可达10 kHz以上。

因此，本文在传统橡胶隔振器阻抗计算中引入了刚度的频散效应，提出了一个刚度随频率变化的计算公式，并通过实验验证其在提高计算精度方面的有效性，同时，利用加速度测量方法避免了力传感器安装复杂、频响有限等不足。

1基于四端参数的阻抗分析

机械阻抗定义为结构所受激励与速度响应的比值，其表达式为：

(1)

式中：Fi代表作用在i点的激励力，Vj代表j点的速度响应，当i=j时，Zij为输入阻抗，当i≠j时，Zij为传递阻抗。

舰船上各类设备常通过橡胶隔振器安装在基座或船体结构上，由离散动力学分析[10]，当隔振器质量远低于被隔离设备时，隔振器可简化为图1所示模型。其中，k和c代表隔振器等效刚度和阻尼，并将其质量等效到上、下两端，分别记为M1和M2。

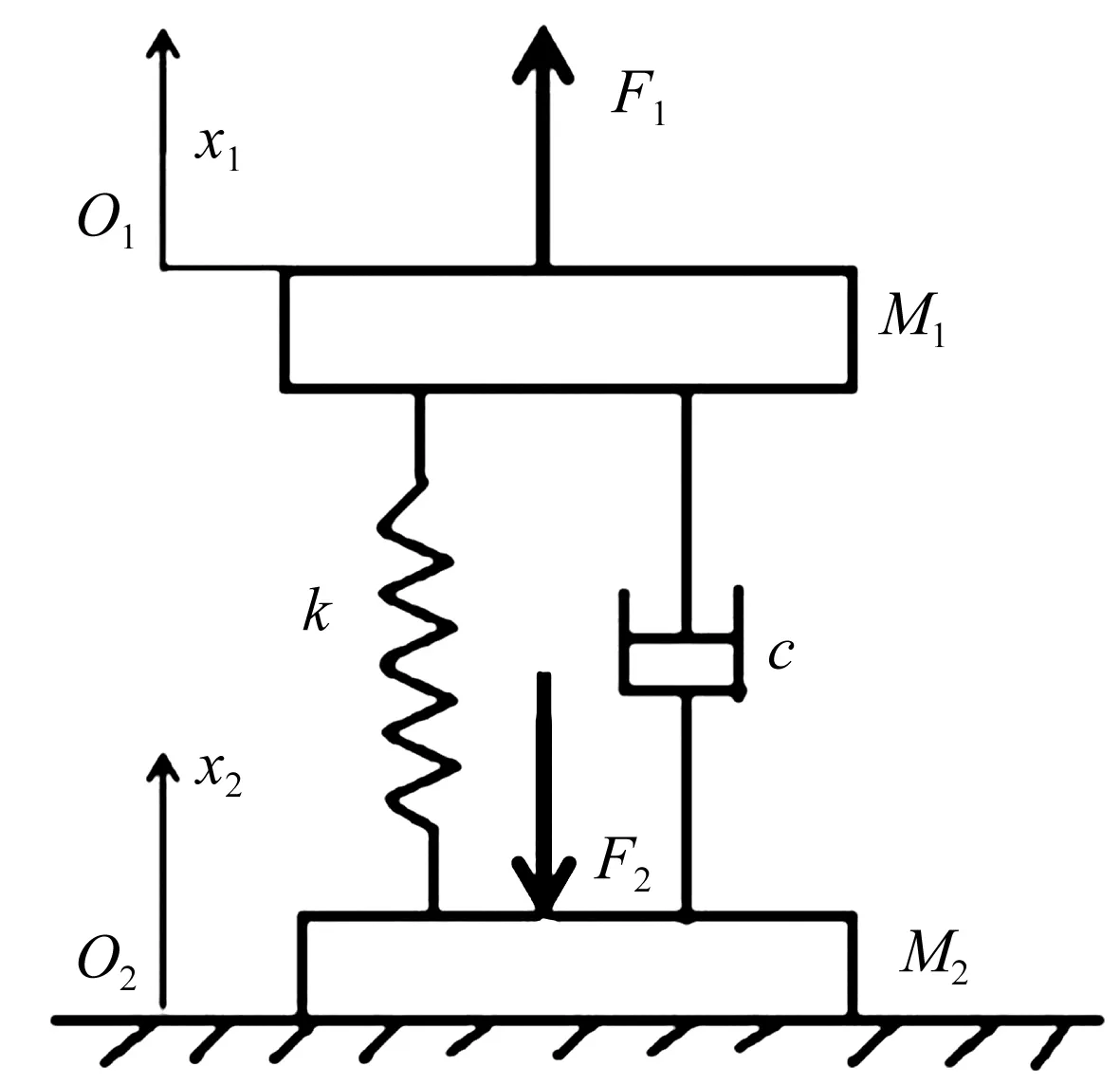
图1　隔振器简化模型Fig.1 Simplified model of rubber isolator

在M1、M2上分别建立广义坐标系O1x1和O2x2，隔振器的四端参数方程可表示为：

(2)

式中，Z11、Z22为隔振器输入阻抗，Z12、Z21为传递阻抗。根据麦克斯维尔的互易性定理，线性定常系统的传递阻抗满足式(3)，对于对称结构的隔振器，还满足式(4)：

Z12=Z21

(3)

Z11=Z22

(4)

通常，隔振器的下端固定于基座上，上端与设备相连，设隔振器上端受到简谐激励为F1=F1ejωt，其相对于固定地面的位移为x=xej(ωt-φ)，当基础刚度足够大时有：

(5)

因此，上表面输入阻抗可写成：

(6)

将式(6)代入式(2)即可求得传递阻抗Z12。

2刚度的频散

当隔振器形状尺寸一定时，刚度取决于橡胶的杨氏模量。文献[11]对多种常用混合胶料进行了试验研究，比较分析了试验温度、外载频率对混合胶料动态模量的影响，如图2，从中可以看出，在一定温度下胶料的弹性模量随频率基本成对数规律变化。由此归纳出一个在特定温度下橡胶隔振器刚度随频率变化的计算公式：

k(f)=Aln(f+B)+C

(7)

图2　文献[11]中两种黏弹性材料动模量特性Fig.2 Two kinds of viscoelastic material’s Young modulus characteristics in literature[11]

A为与胶料和隔振器外形尺寸相关的系数，可由下式确定：

(8)

式中,S为隔振器截面积，h为隔振器高度，a为与胶料相关的经验系数(对天然橡胶，a=(1.50～1.70)×104；丁晴橡胶，a=(1.65～1.85)×104)；B、C为待定参数，在特定温度下可根据特定温度下的静刚度ks和隔振器固有频率fn及相应的动刚度kd来确定。

工程中，可根据国标[13]测定隔振器在某温度下的ks、fn和kd，并代入式(7)得：

(9)

求解得：

(10)

将A、B、C代入式(7)，便得到该温度下的隔振器刚度频散曲线。

图3所示的是某型橡胶隔振器在常温下利用上述计算公式拟合的刚度频散特性曲线及其与实测结果[7]的比较。由图可见，测量数据在恒温下橡胶隔振器刚度与频率基本成对数规律变化，拟合曲线与实测结果能较好地吻合，验证了式(7)的有效性。

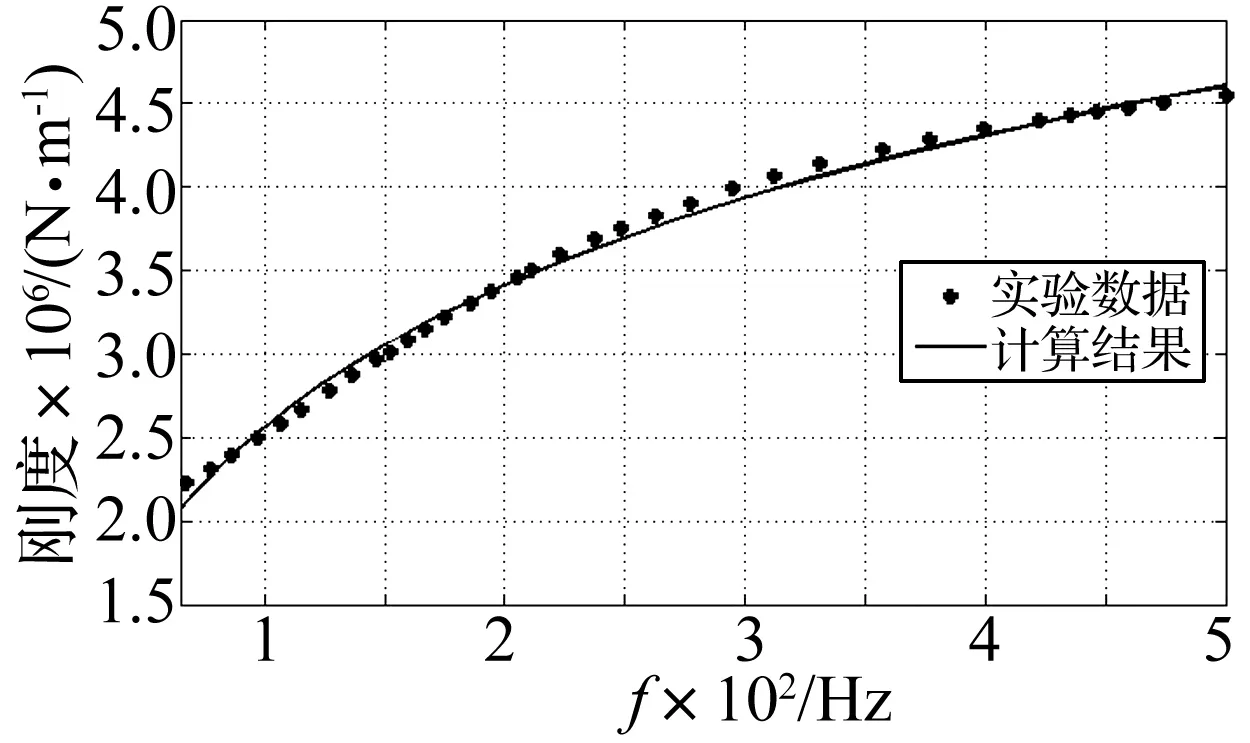
图3　橡胶隔振器刚度随频率变化曲线Fig.3 Function curve between stiffness of rubber isolator and frequency

3基于加速度测量的阻抗测试

3.1测试原理

为了测定刚度频散对橡胶隔振器阻抗计算精度的影响，对两型橡胶隔振器进行了阻抗测试。考虑到力传感器安装复杂、频响有限等不足，本文采用了一种仅基于加速度测量的测试方法，实物图及测试系统原理图见图4和5。

图5中，m1代表激振器和配重的总质量，k1、c1代表用来悬挂激振器的柔性橡胶绳的刚度及阻尼，m2代表基座质量，k2、c2代表支撑基座的气囊或悬挂基座的橡胶绳的刚度及阻尼。a0、a1和a2为加速度传感器，分别用于获取激振器、隔振器上端和基座的运动信号。调节k1使激振器的固有频率远低于隔振器的固有频率以模拟自由边界。

图4　隔振器阻抗测试台架Fig.4 Isolator impedance testing device

根据式(2)，该系统的四段参数方程可表示为：

(11)

F1、F2分别为隔振器受到的来自激振器和基座的力，设定其方向如图1所示，设激振器的激励频率为ω，则应有如下关系式：

(12)

图5　隔振器阻抗测试原理图Fig.5 Isolator impedance testing principle

当配重质量足够大，激振器连杆质量足够小而刚度足够大时，激振器m1和基座m2的平衡方程可写成：

(13)

将式(12)、(13)代入隔振器阻抗表达式(11)并化简得到：

(14)

当基座固定安装在地面上的时候，a2=0，由式(14)可得到输入阻抗的计算式：

(15)

(16)

3.2测试结果与分析

图6是A、B两型隔振器用两种阻抗测量方法得到的结果，测试1、测试2分别代表基于本文提出的加速度测试方法和传统的采用力传感器的测试方法[9]。从图中可见，两种测试方法所得结果在较宽频段内吻合度较高，说明基于加速度测量的阻抗测试方法可行。

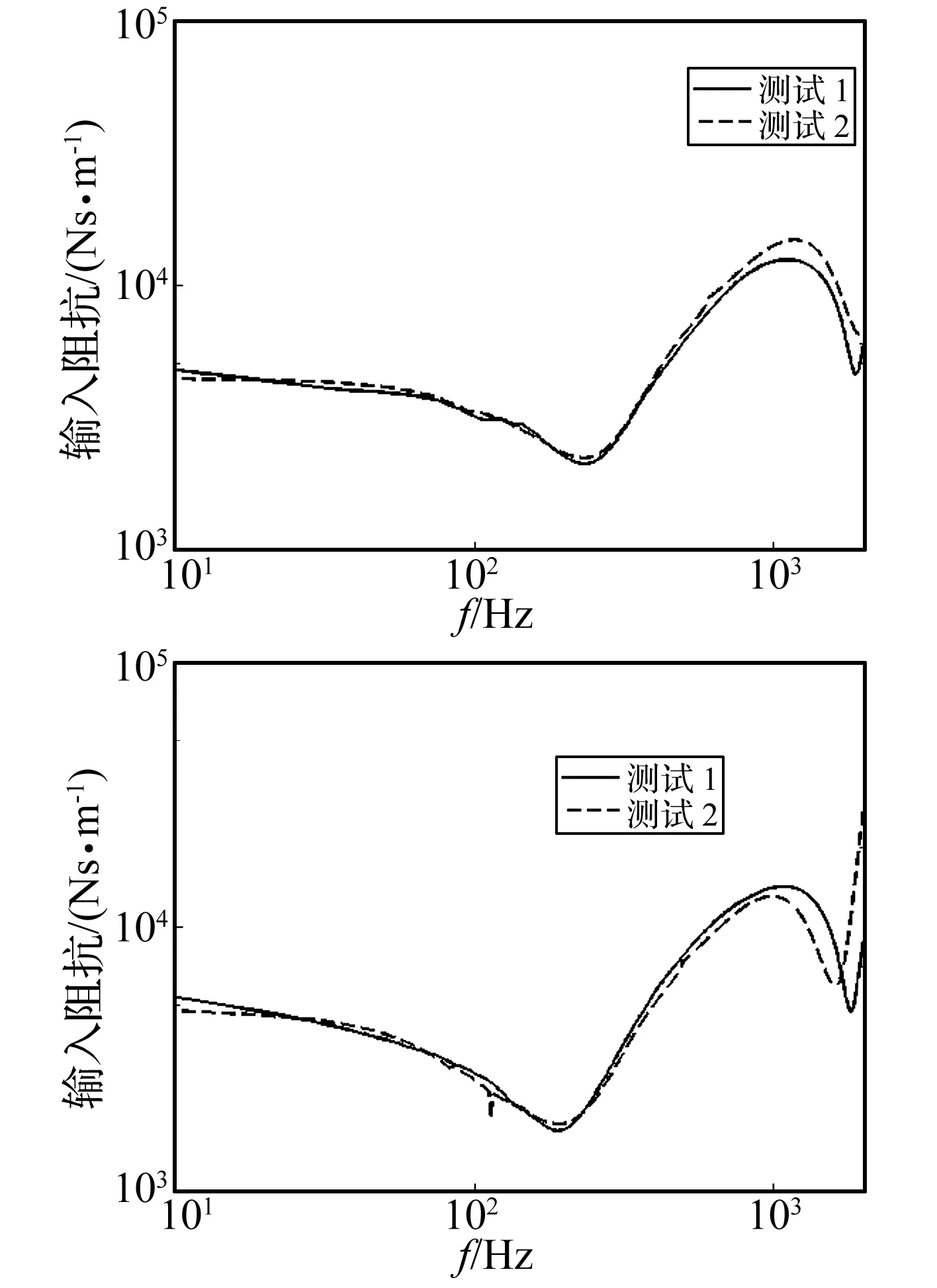
图6　A、B两型隔振器阻抗测试结果Fig.6 Impedance results of isolator A and Bby testing

图7是对A、B两型隔振器进行考虑刚度频散的阻抗计算、定刚度计算与实验测量的结果比对，理论曲线1代表考虑刚度频散的阻抗计算，曲线2、3是定刚度阻抗计算(其中曲线2以静刚度为等效刚度，曲线3以动刚度为等效刚度)。

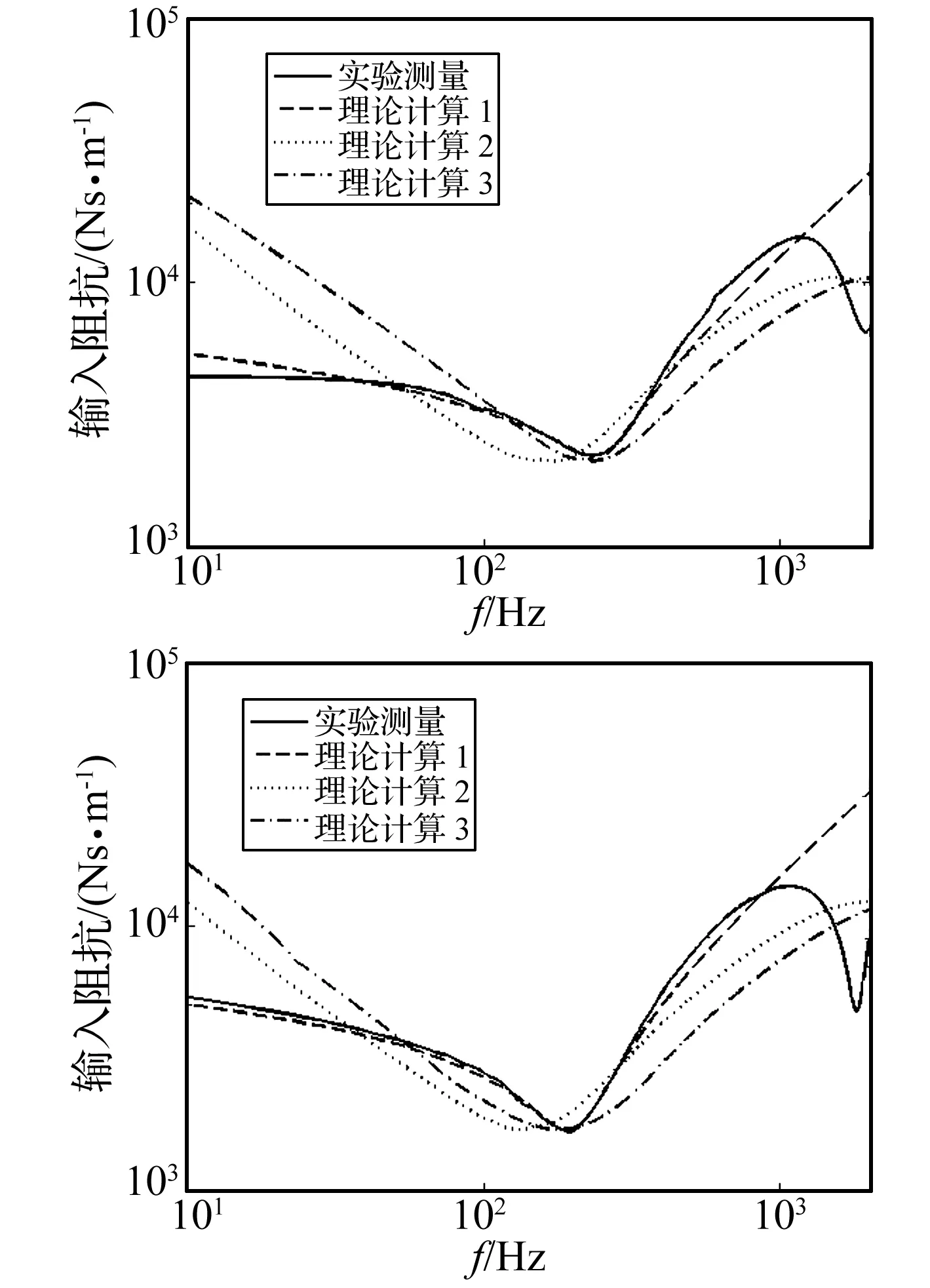
图7　A、B型隔振器阻抗三种理论方法对比Fig.7 Impedance results of isolator A and B in three theoretic ways

通过对图中各曲线的对比可得：① 各理论计算结果与实测结果在1 000 Hz一下变化趋势一致，在低频段，隔振器简化模型可行；② 考虑刚度频散的阻抗计算与实测结果偏差最小，能提高阻抗理论计算的精度；③ 定刚度阻抗计算中，参考动刚度相比于参考静刚度所得曲线与实测结果更吻合，在难以获得刚度频散规律时，以动刚度为参考精度更高；④ 在1 000 Hz以上，实验测量曲线明显下降并回升，形成一个低谷，这是由于隔振器在高频时本身高阶模态被激发，形成“驻波效应”，此时，简化模型不再可行。

4结论

在传统的基于四段参数法的隔振器阻抗计算中引入刚度的频散效应，根据隔振器的尺寸及动、静参数给出了刚度的频散计算公式，并提出了一种简化的基于加速度测量的阻抗测试方法以验证该公式的可行性，由不同假设下的理论计算结果与实测结果比较可得：

(1) 在较宽频段(10～1 000 Hz)内，考虑刚度频散特性能有效提高橡胶隔振器阻抗计算精度；

(2) 基于纯加速度测量的阻抗测试方法在工程测试上有效可行，能避免力传感器安装繁杂、频响有限等问题；

(3) 对结构设计复杂的橡胶隔振器进行数值模拟分析时，可参照本文提出的方法计入杨氏模量的频散特性以提高分析精度。

参 考 文 献

[1] Cemer L,Heckl M,Ungar E E．Structure-borne sound[M]．Berlin:Springer-Verlag，1988.

[2] 潘孝勇,上官文斌,柴国钟,等. 基于超弹性、分数导数和摩擦模型的碳黑填充橡胶隔振器动态建模[J]. 振动与冲击，2007,26(10)：6-10.

PAN Xiao-yong,SHANGGUAN Wen-bin,CHAI Guo-zhong,et al. Dynamic modeling for carbon filled rubber isolators based on hyperelasticity,fractional derivative and a general ized frictional model[J]. Journal of vibration and shock,2007,26(10)：6-10.

[3] 赵广,刘健,刘占生. 橡胶隔振器非线性动力学模型理论与实验研究[J]. 振动与冲击，2010,29(1)：173-177.

ZHAO Guang,LIU Jian,LIU Zhan-sheng. Theoretical and experimental study on nonlinear dynamic model of rubber isolator[J]. Journal of Vibration and Shock,2010,29(1)：173-177.

[4] 范宣华,胡绍全,张志旭,等. 考虑刚度非线性的某橡胶隔振试件随机振动试验仿真研究[J]. 振动与冲击，2009,28(1)：174-176.

FAN Xuan-hua,HU Shao-quan,ZHANG Zhi-xu,et al. Random vibration test simulation for a specimen with vibration-isolating rubber considering stiffness nonlinearity[J]. Journal of Vibration and Shock,2009,28(1)：174-176.

[5] 陈辉， 王韶枫， 何斌，等. 多方向冲击条件下隔振器冲击特性试验研究[J]. 振动与冲击，2014,33(8)：209-214.

CHEN Hui,WANG Shao-feng,HE Bin,et al.Tests for shock characteristics of isolators under multidirectional shocks[J]. Journal of Vibration and Shock,2014,33(8)：209-214.

[6] 计方,路晓东,王峰,等. 基于数值试验的减振器阻抗特性研究[J]. 船舶，2013,24(2)：39-44.

JI Fang,LU Xiao-dong,WANG Feng,et al.Numerical experimentation on mechanical impedance of vibration isolator[J].Ship & Boat，2013,24(2)：39-44.

[7] ISO10846,Acoustics and vibration-Laboratory measurement of vibro-acoustic transfer properties of resilient elements(part 1～ part 5) [S].

[8] GB /T 11349.1-1989,机械导纳的试验确定基本定义与传感器[S].北京：中国标准出版社.

[9] GB /T 11349. 2-1989,机械导纳的试验确定用激振器作单点激励测量[S].北京：中国标准出版社.

[10] 陈端石,赵玫,周海亭. 动力机械振动与噪声学[M]. 上海：上海交通大学出版社,2002.

[11] 罗桑,钱振东,HARVEY J. 环氧沥青混合料动态模量及其主曲线研究[J].中国公路学报，2010,23(6)：16-20.

LUO Sang,QIAN Zhen-dong,Harvey J. Research on dynamic modulus for epoxy asphalt mixtures and its master curve[J]. China Journal of Highway and Transport，2010,23(6)：16-20.

[12] 张林啸. 橡胶扭转减振器特性的研究[D]. 广州：华南理工大学，2012.

[13] GB/T 15168-94.振动与冲击隔离器性能测试方法[S].北京：中国标准出版社.

Rubber isolator impedance based on stiffness dispersion

HUANG Wu-de, CHEN Guang-ye, CHE Chi-dong

(School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiao Tong University Shanghai 200240, China)

Abstract:The relationship between stiffness of isolators and their vibration frequency was deduced according to testing results of rubber’s Young’s modulus and stiffness, and isolators’ static stiffness and dynamic stiffness were used to determine relevant coefficients. Stiffness dispersion was brought into theoretical impedance estimation of rubber isolators based on four-polar parameter equations with a higher accuracy. On the other side, an impedance testing method based on acceleration measurement was designed and two types of rubber isolators were tested with this method. Comparing the tested results and the estimation ones under different stiffness modes, it was shown that the impedance estimation is more accurate considering stiffness dispersion was shown and the impedance testing method based on acceleration measurement is feasible.

Key words:isolators; impedance; stiffness dispersion; acceleration measurement

基金项目：国家自然科学基金资助项目(51109131)

收稿日期：2014-11-12修改稿收到日期：2015-05-07

通信作者车驰东 男，博士，副教授，硕士生导师，1980年生

中图分类号:TB52+7

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.026

第一作者 黄伍德 男，硕士生，1993年3月生

E-mail:churchdoor@sjtu.edu.cn