迷宫密封激振力作用下转子系统非线性动力学分析

张恩杰， 焦映厚， 陈照波， 李明章， 刘福利

(哈尔滨工业大学 机电工程学院，哈尔滨　150001)

迷宫密封激振力作用下转子系统非线性动力学分析

张恩杰， 焦映厚， 陈照波， 李明章， 刘福利

(哈尔滨工业大学 机电工程学院，哈尔滨150001)

摘要：由双控体模型确定迷宫密封轴向平均流速，结合Muszynska气流激振力建立了转子-密封系统非线性动力学模型，并采用Runge-Kutta-Fehlbrg方法求解系统非线性动力学方程。分析了迷宫密封间隙、密封半径、齿数、齿腔宽度、进口气压等参数对泄漏量及轴向平均流速的影响；绘制了分岔图、轴心轨迹、Poincare图和频谱图等，研究了转速、进口气压、偏心距及密封有效总长度对系统动力学特性的影响。数值结果表明，转速、密封结构及介质参数的改变能够诱导系统发生单周期运动、概周期运动等复杂的非线性动力学行为。

关键词：迷宫密封；转子；非线性动力学；双控体模型；Muszynska模型

迷宫密封自投入使用近一个世纪以来，科研人员对其进行了广泛研究。Rhode等[1]对密封流场进行了数值模拟，揭示了其密封机理。黄守龙等[2-3]通过分析密封介质流动和泄漏特性，从流动不稳定性方面进一步推进了密封机理研究。Wang等[4-5]对不同结构型式的迷宫密封进行了CFD分析，阐述了结构参数等对泄漏特性的影响；Kim等[6]采用CFD法和解析法，研究了直通型和阶梯齿迷宫密封的齿数、压差等参数对流场分布、流量系数、泄漏特性的影响，并同实验结果进行了对比分析。Kirk等[7-8]研究了偏心率、入口预旋等对交错齿和阶梯齿迷宫密封泄漏量及动力系数等的影响，采用有限元法分析了离心式压缩机转子的稳定性。Li等[9]应用FLUENT识别出Muszynska模型中的经验参数，建立了各向异性转子-密封系统幂级数模型，研究了转子-密封系统1/2亚谐共振及分岔；He等[10-11]基于无量纲化双控体模型，分析了介质性质、结构型式及参数对迷宫密封的动特性系数的影响，求解了转子-密封系统的非线性运动特征；Li等[12]基于Hamilton原理对转子-轴承-密封系统进行了非线性动力学特性分析。

目前，迷宫密封泄漏特性及系统动力学方面的研究尽管很多，但在由密封结构、介质特性变化引起的泄漏量、轴向流速和因此而诱发的系统非线性动力学行为的改变方面，成果却相对较少。因此，本文采用双控体模型分析密封结构和介质对泄漏量、轴向平均流速的影响，建立并求解迷宫密封-转子系统动力学方程，研究密封参数及其引起的轴向平均流速的变化对系统非线性动力学特性的影响。

1迷宫密封-转子系统非线性动力学模型

介质流经直通型迷宫密封时，根据流动特点将腔室划分为射流区Ⅰ和涡流区Ⅱ(如图1所示)。由Scharrer[13]的双控体模型，迷宫密封的泄漏量可表示为：

(1)

式中，

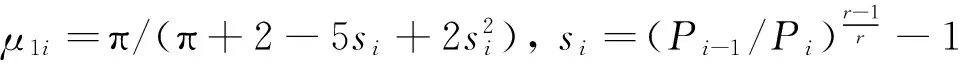
μ2i=(1-α)-1/2, α=8.52/((Li-Tpi)/Cr+7.23)

式中，Ai为密封间隙处圆周面积，Pi为第i齿腔内的气压，R为气体常数，T为密封腔内温度，r为气体绝热指数，Li为密封腔宽度，Tpi为密封齿顶宽度，Cr为密封间隙。

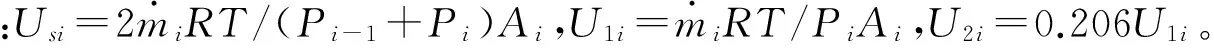
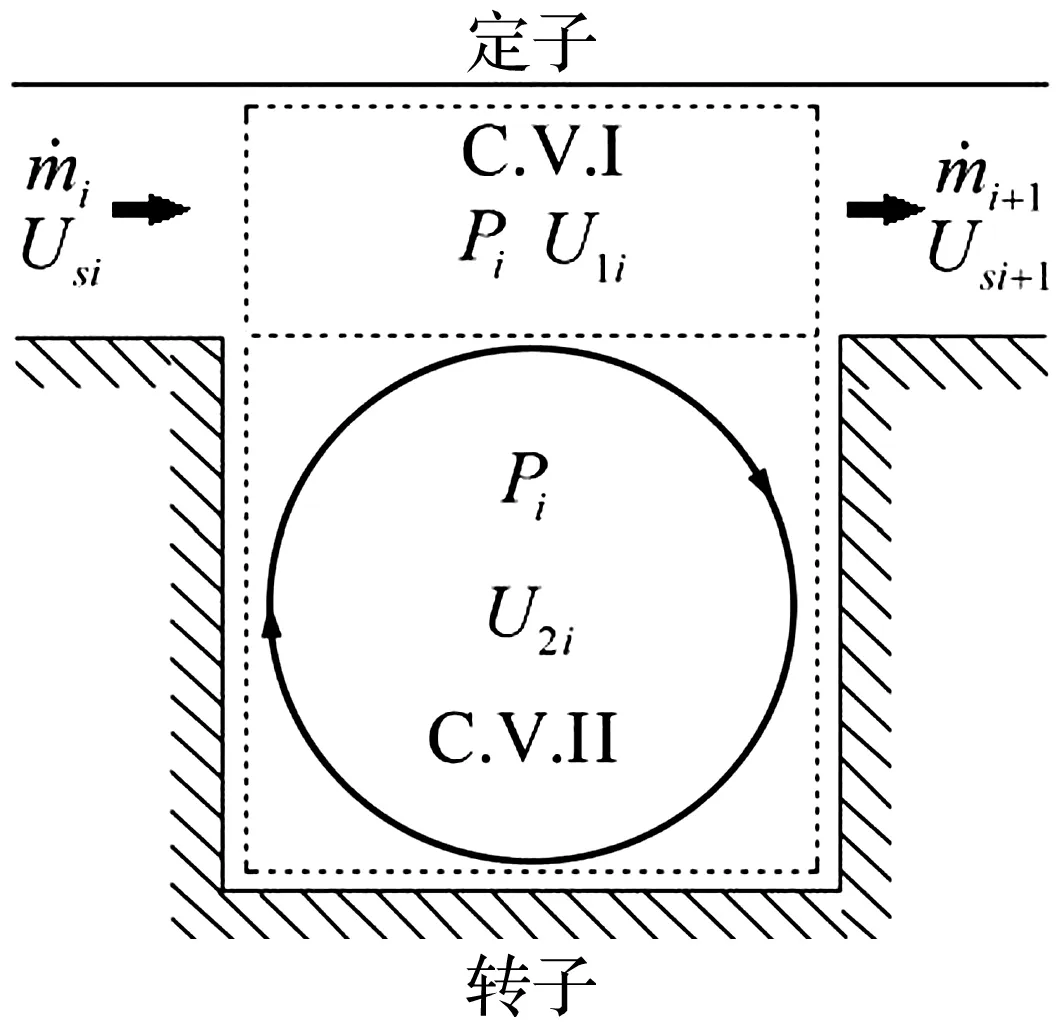
图1　双控体模型示意图Fig.1 Two-control-volume model

介质流经迷宫密封的狭小间隙时，流体作用在转子表面的激振力将诱发系统丰富的非线性动力学行为，严重情况下会造成转子碰摩等故障。将密封流体激振力等效作用于Jeffcott转子-密封系统(如图2)的圆盘中心处，建立系统的非线性动力学模型：

(2)

式中，m为转子横向振动有效质量，rp为偏心距，ω为转子转速，X,Y为转子轴心位移，De、Ke分别为外阻尼系数和转子刚度，FX及FY为Muszynska密封激振力：

(3)

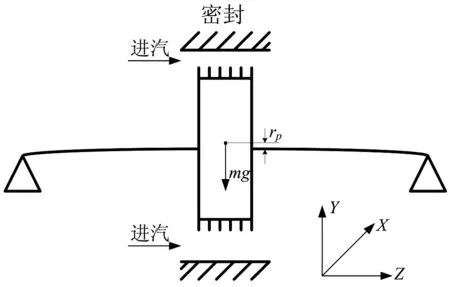
图2　转子-密封系统动力学模型Fig.2 Thedynamic model of rotor-seal system

联立以上各式并对其进行无量纲化处理，最终可得到如下形式的系统动力学方程：

(4)

2迷宫密封-转子系统动力学分析

2.1密封结构及介质参数对密封性能的影响

密封结构形式、密封介质参数决定密封腔内流场分布及动能与内能的交换，进而影响泄漏量及轴向流速。由于密封-转子系统的非线性动力学特性与轴向平均流速等密切相关，有必要分析密封结构和介质参数对泄漏量及轴向流速的影响。

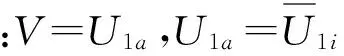
出口为环境大气压，调节迷宫密封入口气压，针对具有不同径向间隙Cr的密封结构(表1)分析其泄漏量及轴向平均流速变化趋势(图4)。相同径向密封间隙的迷宫密封，随着入口气压的增加，每一密封腔内的气压均相应提高，同一密封腔进出口压差增大，由表达式(1)及轴向平均流速计算公式可知，泄漏量随之大幅增加，单位时间内流经相同密封间隙圆周面积的流量增大，则轴向平均流速也有所升高；0.85 MPa时，由于发生末齿节流现象，轴向平均流速略有降低。相同入口气压条件下，密封间隙圆周面积随着径向间隙Cr的增加而增大，泄漏量及轴向平均流速均随之增加。

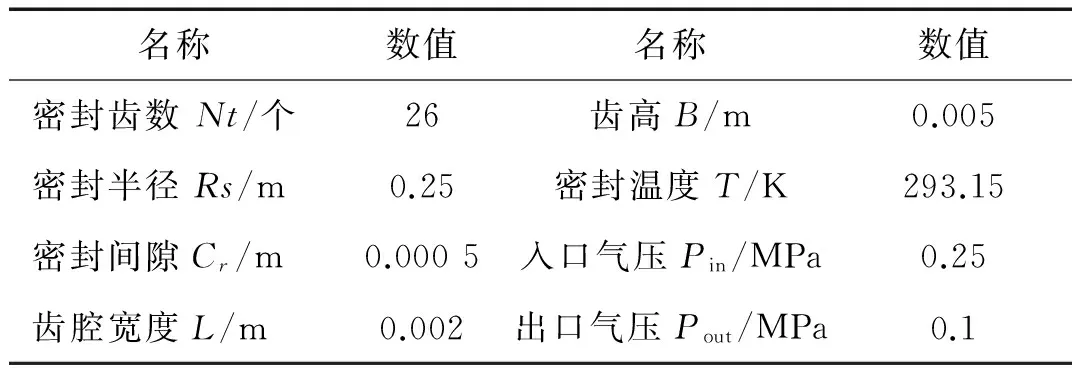
表1　迷宫密封结构参数及工作条件

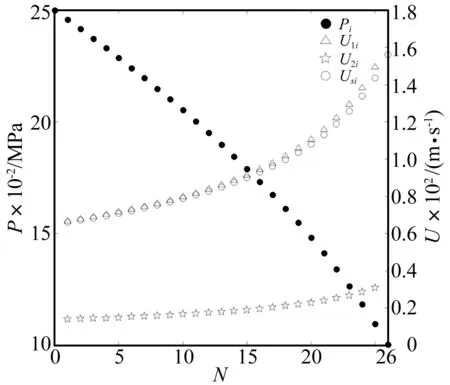
图3　平均气压及轴向流速分布Fig.3 Distributions of mean pressure and axial velocity in cavities

工作于不同入口气压条件下的迷宫密封(表1),保持齿腔宽度或齿数不变，分别增加齿数(图5)和齿腔宽度(图6)，则密封有效长度均线性增大，密封腔中流体的动能同内能的交换加剧，密封节流效果加强，泄漏量及轴向平均流速均随之降低；当齿数/齿宽增加到一定程度时，泄漏量及轴向平均流速趋于定值，密封节流作用不能随着齿数/齿腔宽度的增加而无限增强。迷宫密封进出口压差的减小能够降低轴向平均流速和泄漏量，在提高密封性能的操作中较易实现。

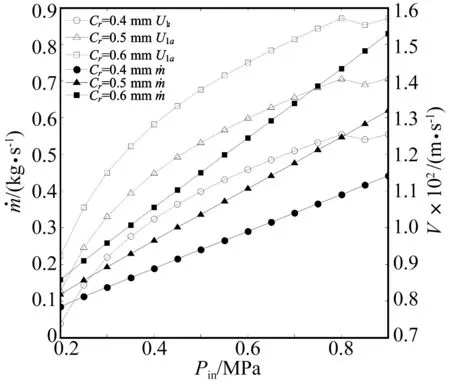
图4　泄漏量及轴向平均流速随入口气压的变化Fig.4 Variation of leakage flow and axial mean velocity in respect to the inlet pressure

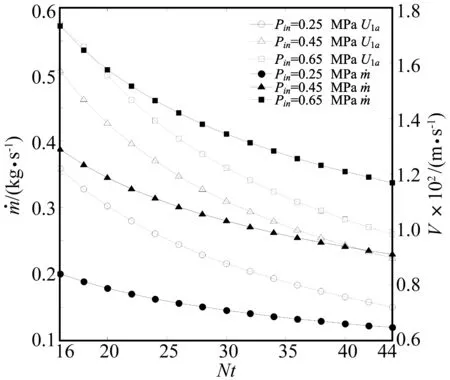
图5　泄漏量及轴向平均流速随齿数的变化Fig.5 Variation of leakage flow and axial mean velocity in respect to thenumber of seal strips

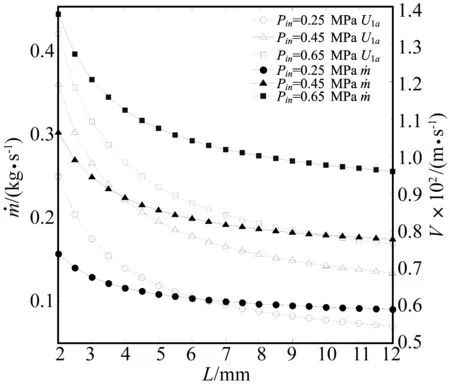
图6　泄漏量及轴向平均流速随齿腔宽度的变化Fig.6 Variation of leakage flow and axial mean velocity in respect to the cavity-width

图7为密封半径对三种进口气压下工作的迷宫密封(表1)的泄漏量及轴向平均流速影响的分析图。相同进口气压条件下，密封半径的增加使得单位长度的环向面积Ai增大，泄漏量随之单调增加；由双控体模型中关于泄漏量及轴向平均流速的计算公式可知：

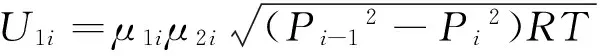
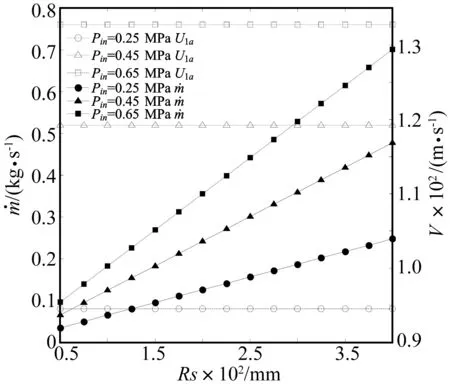
图7　泄漏量及轴向平均流速随密封半径的变化Fig.7 Variation of leakage flow and axial mean velocity in respect to the rotor-radius

2.2转速对迷宫密封-转子系统动力学特性的影响

将采用双控体模型求得的迷宫密封轴向平均流速引入到方程(4)中，采用Runge-Kutta-Fehlbrg方法对其进行求解，分析转速对系统非线性动力学行为的影响。所选取的迷宫密封结构参数见表1，转子参数为：m=200 kg，Ke=107N/m，De=500 Ns/m，rp=0.15 mm。

图8为转子轴心在x方向无量纲位移随转速变化的分岔图，升速过程中系统的非线性动力学行为非常丰富。在ω≤187 rad/s低速运转时，方程(4)存在唯一解，系统此时为单周期运动；随着转速的增加，流体对转子的作用增强，轴心位移幅值不断增大。187 rad/s <ω≤200 rad/s时，系统发生分岔，表现为概周期或n-T周期运动。在随后的升速过程中，系统又多次经历了倍周期运动、概周期运动等运动形式。

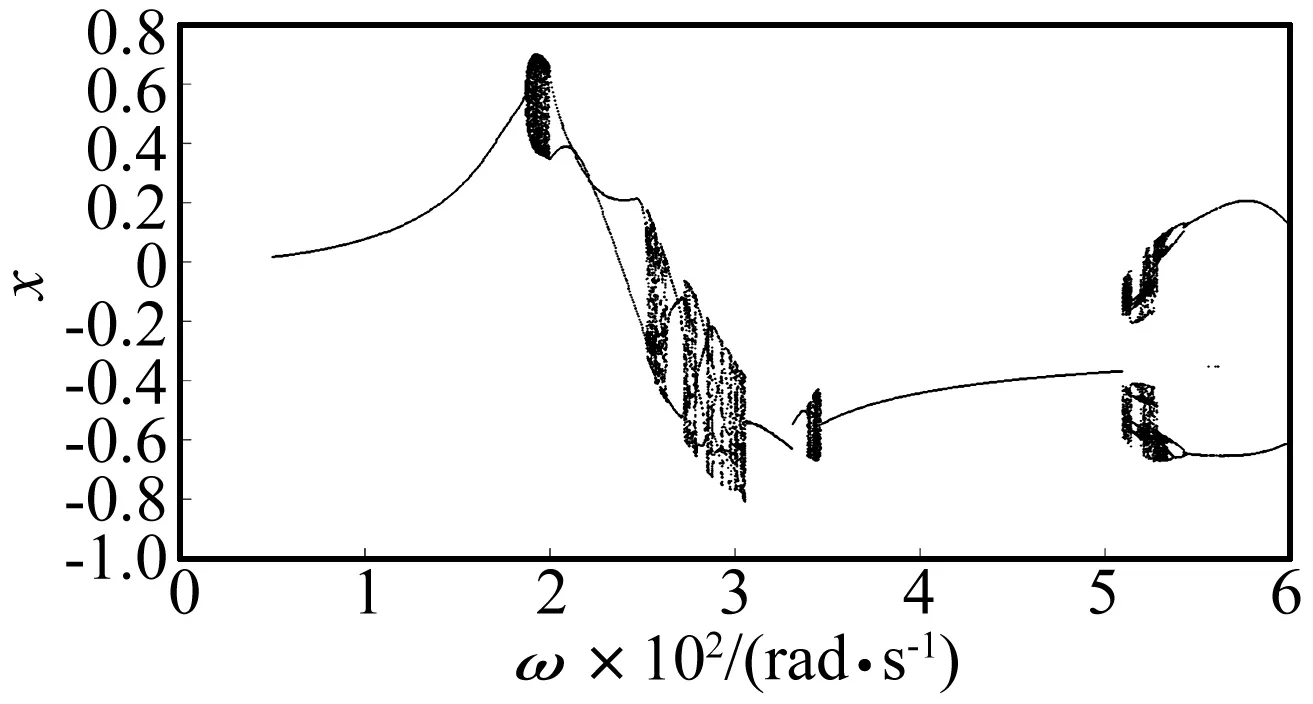
图8　转子轴心在x方向分岔图Fig.8 Rotor center bifurcation diagram in x direction

图9为ω=195 rad/s时的运动分析图，由时间历程图可知，此时系统并非单周期运动或倍周期运动，轴心轨迹图和相图中为多个永不重复的大小相套的椭圆环，Poincare图中的点趋向构成一条封闭的曲线，表明密封-转子系统此时经历着概周期运动。频谱图中以1倍频和1.42倍频为主，同时存在0.42倍频等频率成分。

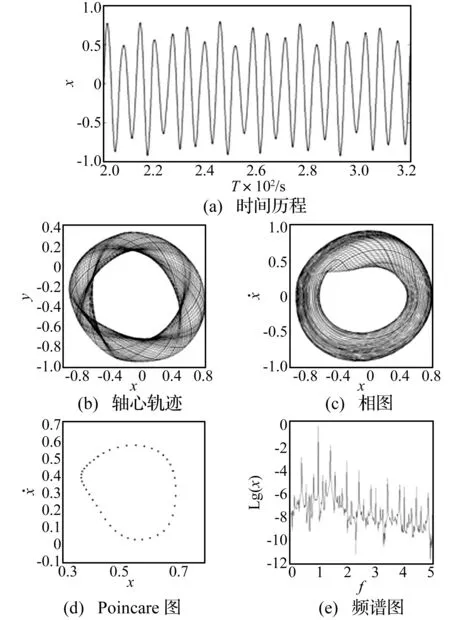
图9　ω=195 rad/s时系统响应图Fig.9 Dynamic response diagram of system at ω=195 rad/s

2.3结构和介质参数对系统非线性动力学特性的影响

汽轮机转子系统在某些工况需要在定转速下调整进口气压或压比，以适应实际负载需求。进口气压的变化使得轴向平均流速发生改变，而流速与压差则同时对密封-转子系统的动力学特性产生影响。分析进口气压对系统非线性动力学特征的影响时，每一计算步都需首先由双控体模型求得相应进口气压条件下的轴向平均流速，进而分析压差与轴向平均流速的耦合作用。

图10为进口气压对系统动力学特征影响的分岔图，其中结构参数及其它介质参数与2.2节中相同。由0.2 MPa加压到0.3 MPa的过程中，系统首先从单周期运动转变为概周期运动，在Pin=0.29 Mpa时，由4-T周期运动转化为倍周期运动。对比该图中进口气压为0.25 MPa及图8中ω=530 rad/s时的运动特征，转子轴心在x方向的无量纲位移在分岔图中均显示为两组不同坐标的点，为概周期运动，二者的运动形式一致，为系统在相同结构及进口气压条件下的运动响应。随后进口气压由0.3 MPa增加到1 MPa时，系统依次经历了倍周期运动和单周期运动。可见进口气压对系统动力学行为的影响非常显著。

转子平衡一般通过加平衡重量调节偏心距来实现，偏心距对密封-转子系统的非线性动力学特性会造成一定的影响。图11为ω=530 rad/s时，调节转子偏心距(其余参数与2.2节中相同)得到的分岔图。当偏心距rp=0～0.113 mm变化时，系统为同步振动；增大偏心距，轴心位移增加，系统存在单周期运动、倍周期运动和概周期运动等运动形式；当rp=0.176 mm时，转子概周期运动的轴心最大无量纲位移接近-1，系统发生碰摩的几率增加。

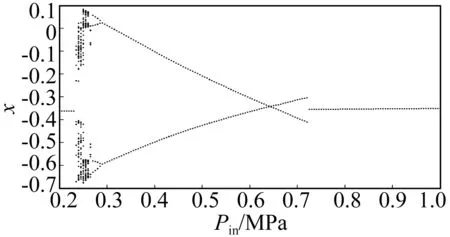
图10　转子响应随进口气压变化分岔图(ω=530 rad/s)Fig.10 Bifurcation diagram of the rotor with inlet pressure varying (ω=530 rad/s)

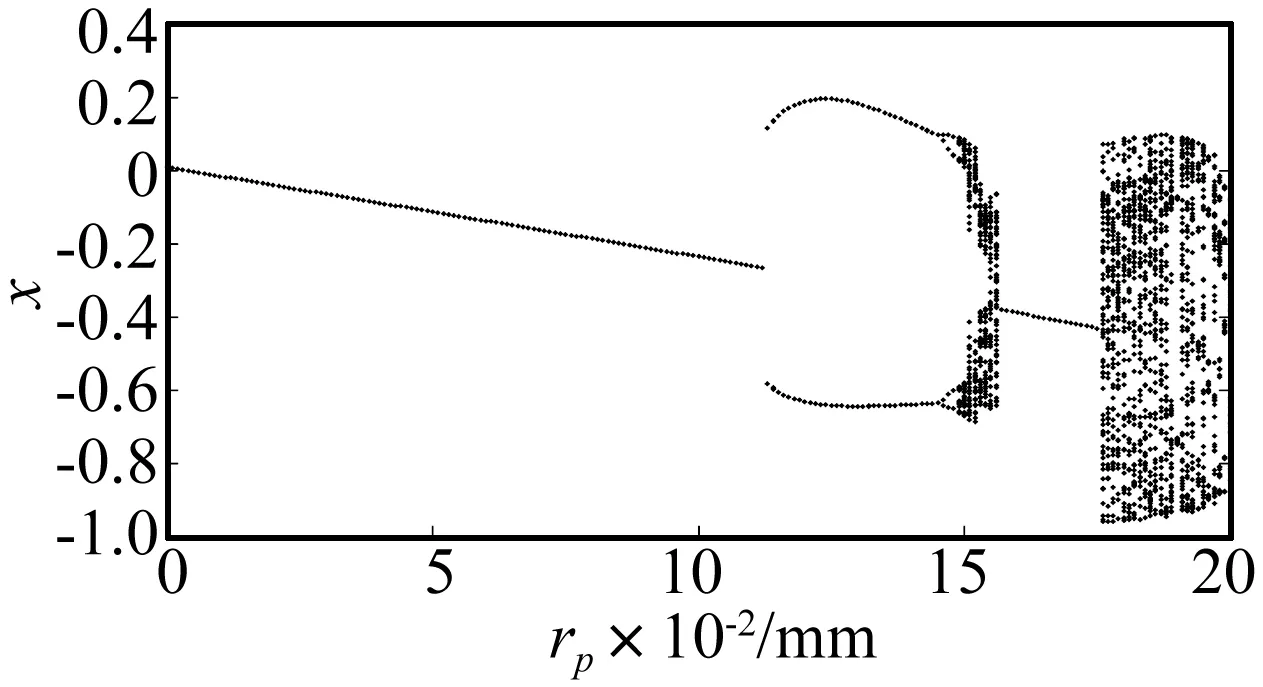
图11　转子响应随偏心距变化分岔图(ω=530 rad/s)Fig.11 Bifurcation diagram of the rotor with eccentricity varying (ω=530 rad/s)

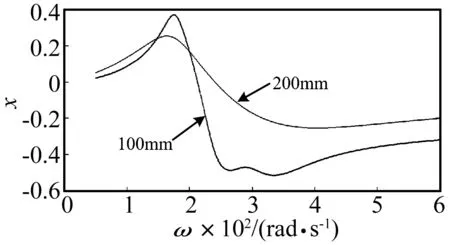
图12　转子响应随密封长度变化分岔图Fig.12 Bifurcation diagram of the rotor with effective seal-length varying

迷宫密封的齿数及齿腔宽度均直接决定密封有效总长度，气压分布、密封轴向平均流速及密封激振力等也因其不同而产生相应改变，迷宫密封-转子系统非线性动力学特征同样随之变化。图12为密封有效总长度为100 mm和200 mm时(其余参数与2.2节中相同)得到的系统分岔图。由图可见，密封长度增加后，系统不再存在倍周期、概周期、混沌等复杂动力学行为，仅为单周期运动；同时，密封长度的增加使得轴向平均流速有所降低，在密封激振力的作用下，转子轴心无量纲位移总体减小。图中，密封有效总长度仅由齿腔宽度决定，分别为4 mm和8 mm；密封有效总长度由齿数或齿腔宽度决定所得到的系统动力学特征基本相同。

3结论

本文采用双控体模型和Muszynska密封激振力建立了迷宫密封-转子系统非线性动力学模型，分析了迷宫密封内平均气压及轴向流速分布，研究了密封结构及介质参数对密封泄漏量和轴向平均流速的影响，得到了转子转速、进口气压、偏心距、齿数和齿宽对系统非线性动力学特性影响的分岔图。分析结果表明：

(1) 密封泄漏量随入口气压、密封间隙及密封半径的增加而增大，随齿数和齿腔宽度的增加而减小；轴向平均流速随入口气压、密封间隙的增加而增大，随齿数和齿腔宽度的增加而降低，密封半径对其没有影响。

(2) 转子系统在升速过程中存在丰富的非线性动力学行为，进口气压对系统动力学特征的影响非常显著，偏心距的增大使得转子轴心位移总体增大，发生碰摩的几率增加，迷宫密封的齿数及齿腔宽度对系统动力学特征的影响基本相同，有效密封总长度的增加明显改变系统的非线性动力学特性。

参 考 文 献

[1] Rhode D A,Demko J A,Traigner U K,et al. The prediction of incompressible flow in labyrinth seals[J]. Journal of Fluids Engineering,1986,108(1):19-25.

[2] 黄守龙，王建中. 流动不稳定性对迷宫密封效率的影响[J]. 武汉工业大学学报，1999，21(1):44-47.

HUANG Shou-long,WANG Jian-zhong. The influence of flow instability on labyrinth seal efficiency[J]. Journal of Wuhan University of Technology,1999,21(1):44-47.

[3] 黄守龙，马毓义，吴晓松，等. 迷宫通道内部流动和泄漏特性的数值分析[J]. 航空动力学报，1995，10(2):135-138.HUANG Shou-long,MA Yu-yi,WU Xiao-song,et al. Numerical analysis of flow and leakage in labyrinth seal[J]. Journal of Aerospace Power,1995,10(2):135-138.

[4] Wang W Z,Liu Y Z,Meng G,et al. Influence of rub groove on rotordynamics associated with leakage air flow through a labyrinth seal[J]. Journal of Mechanical Science and Technology,2010,24 (8):1573-1581.

[5] Zhao W,Nielsen T K,Billdal J T. Effects of cavity on leakage loss in straight-through labyrinth seals [C]// IOP. Proceedings of 25th IAHR Symposium on Hydraulic Machinery and Systems. Timisoara,Romania:IOP Publishing,2010. 012002.

[6] Kim T S,Cha K S. Comparative analysis of the influence of labyrinth seal configuration on leakage behavior[J]. Journal of Mechanical Science and Technology,2009,23(10):2830-2838.

[7] Kirk G,Gao R. Influence of preswirl on rotordynamic characteristics of labyrinth seals[J]. Tribology Transactions,2012,55(3):357-364.

[8] Gao R,Kirk G. CFD study on stepped and drum balance labyrinth seal[J]. Tribology Transactions,2013,56(4):663-671.

[9] Li Z G,Chen Y S. Research on 1∶2 subharmonic resonance and bifurcation of the nonlinear rotor-seal system[J]. Applied Mathematics and Mechanics,2012,33(4):499-510.

[10] He H J,Jing J P. Research into the dynamic coefficient of the rotor-seal system for teeth-on-stator and teeth-on-rotor based on an improved nonlinear seal force model[J]. Journal of Vibration and Control,2014,20(15):2288-2299.

[11] 何洪军，荆建平. 非线性转子-密封系统动力学模型研究[J]. 振动与冲击，2014，33(10):73-76.

HE Hong-jun,JING Jian-ping. Dynamic model of a nonlinear rotor-seal system[J]. Journal of Vibration and Shock,2014,33(10):73-76.

[12] Li W,Yang Y,Sheng D R,et al. A novel nonlinear model of rotor-bearing-seal system and numerical analysis[J]. Mechanism and Machine Theory,2011,46(5):618-631.

[13] Scharrer J. A comparison of experimental and theoretical results for labyrinth gas seals [D]. Texas:Texas A&M University,1987.

[14] Childs D W. Dynamic analysis of turbulent annular seals based on hirs lubrication equation[J]. Journal of Lubrication Technology,1983,105(3):429-436.

Nonlinear dynamic analysis of a rotor system excited by labyrinth seal force

ZHANG En-jie, JIAO Ying-hou, CHEN Zhao-bo, LI Ming-zhang, LIU Fu-li

(School of Mechatronic Engineering, Harbin Institute of Technology, Harbin 150001, China)

Abstract:Here, the nonlinear dynamic model of a labyrinth seal-rotor system was built using Muszynska’s nonlinear seal forces. In the process of nonlinear dynamic analysis, the axial mean flow velocity of the labyrinth seal was determined with the two-control-volume model. Applying Runge-Kutta-Fehlbrg numerical integration, the nonlinear dynamic equation of the system was solved. The effects of parameters, such as, labyrinth seal clearance, seal-radius, number of seal strips, cavity-width and inlet air pressure on leakage and axial mean flow velocity were analyzed. The influences of rotational speed, inlet air pressure, eccentricity and effective seal-length on the nonlinear dynamic characteristics of the system were also studied. The nonlinear dynamic properties of the system were described with bifurcation diagrams, axis orbits, Poincare Maps and frequency spectra. The numerical results showed that the changing of rotating speed, seal geometry and seal medium parameters can induce abundant nonlinear dynamical behaviors like periodic motion and quasi-periodic motion, etc.

Key words:labyrinth seal; rotor; nonlinear dynamics; two-control-volume model; Muszynska model

基金项目：国家自然科学基金(11272100)

收稿日期：2015-03-06修改稿收到日期：2015-04-29

通信作者焦映厚 男，教授，博士生导师，1962年生

中图分类号:O322；TH113.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.025

第一作者 张恩杰 男，博士生，1987年生

E-mail:jiaoyh@hit.edu.cn