基于MMSE和ABCSVM的液压泵故障模式识别

李洪儒， 王余奎,2， 马济乔， 叶　鹏

(1. 军械工程学院, 石家庄　050003; 2. 空军勤务学院, 徐州　221000)

基于MMSE和ABCSVM的液压泵故障模式识别

李洪儒1， 王余奎1,2， 马济乔1， 叶鹏1

(1. 军械工程学院, 石家庄050003; 2. 空军勤务学院, 徐州221000)

摘要：为了更好地实现液压泵的故障模式识别，对液压泵故障特征提取方法和模式识别方法进行研究。针对多尺度熵算法存在的在尺度因子较大时时间序列较短而导致各尺度样本熵表征液压泵故障状态性能较差的问题，提出了改进的多尺度熵算法，通过对液压泵实测信号分析验证了所提出的改进多尺度熵的良好性能。针对液压泵故障状态与故障特征之间的非线性关系，采用支持向量机算法建立液压泵的故障模式识别模型，并提出采用人工蜂群优化算法对支持向量机模型参数进行优化。基于改进多尺度熵和蜂群优化参数的支持向量机实现液压泵故障模式识别，通过对比分析验证了所提出的液压泵故障模式识别方法的良好性能。

关键词：液压泵；模式识别；改进多尺度熵；人工蜂群算法；SVM

由于液压油的压缩性、泵源与液压回路的流固耦合作用以及工作过程中泵体本身固有的机械冲击，导致液压泵的振动信号表现出很强的非平稳、非线性特性。因此，从非线性、非平稳信号中提取故障特征信息成为液压泵故障模式识别的关键。近年来，随着非线性理论地发展，很多非线性分析方法，如小波分析[1]、分形维数[2]、K熵[3]等已被广泛应用于机械设备故障识别领域，极大地丰富了故障识别的技术和手段。文献[4]提出了一种计算时间序列复杂度的方法——样本熵(Sample Entropy, Samp En)。与Lyapunov指数、信息熵[5]、关联维数[6]和K熵等非线性动力学方法相比，样本熵不仅具有得到稳定估计值所需数据短的优点，而且在参数大范围取值的情况下具有很好的一致性[7]。文献[8]将样本熵与集成经验模式分解方法相结合，应用到轴承的故障诊断中，很好地识别出轴承的不同类型故障。文献[9]提出了一种结合小波变换和样本熵的特征提取方法，通过小波变换，把脑电信号进行3层分解，抽取出小波系数的能量均值和能量均差值，并结合脑电信号的样本熵组成特征向量，输入SVM分类器中，实现了左右手运动想象脑电信号的分类。虽然样本熵在特征提取方面取得了一定的成果，但是，样本熵只能衡量时间序列在单一尺度上的复杂性，针对该问题文献[10]在样本熵的基础上，提出了另一种时间序列复杂度的衡量方法——多尺度熵(Multiscale Entropy,MSE)，用以衡量时间序列在不同尺度上的复杂性，极大地丰富了熵的含义。文献[11]将多尺度熵应用于转子故障信号复杂性地度量中，提取出了转子的故障特征，并与样本熵进行了对比，结果表明多尺度熵更能有效地实现转子故障类型的诊断。文献[12]将轴承振动信号多尺度熵的统计分量作为特征向量，利用自适应模糊神经网络进行故障诊断，取得了很好的诊断效果。多尺度熵解决了样本熵只能在单一尺度上度量时间序列复杂度的问题，但是在重构时间序列时，MSE算法极大地缩短了原始时间序列的长度，这样必然会降低不同时间尺度上样本熵计算的准确度，甚至可能产生无关的熵值。因此，有必要对MSE算法进行研究，分析其用于液压泵故障特征提取的性能，针对其不足进行改进，以提高所提取故障特征表征液压泵状态的性能。

支持向量机(Support Vector Machine，SVM)是继神经网络之后又一研究热点，其核心思想是使样本之间的分类间隔最大化，它在解决小样本、高维数模式识别问题上表现出非常好的性能。由于SVM特别适合小样本策略，因此其被广泛应用于故障模式识别和故障预测等领域。文献[13]将8层节点分解的样本熵作为特征向量，利用粒子群算法优化后的SVM对滚动轴承进行故障诊断。文献[14]提出了一种基于小波包变换、邻域粗糙集和SVM的机械故障诊断方法，并通过实例验证了该方法的有效性。文献[15]将D-S证据理论和SVM算法相融合，提出了一种多数据融合故障诊断新方法。SVM虽然在小样本学习、非线性、高维问题和泛化能力方面表现出了很好的特性，但SVM的模式识别正确率很大程度上取决于核函数的种类及参数，本文利用ABC算法对SVM的参数进行优化，利用优化后的SVM对液压泵进行故障模式识别，以期得到更高的故障识别率。

本文以液压泵故障模式识别为目的，对液压泵故障特征提取方法和模式识别方法进行研究。通过对MSE算法进行研究，针对其存在的问题提出了MMSE算法，对液压泵振动信号分析提取MMSE作为其故障特征。采用SVM算法建立液压泵的故障识别模型，并提出采用ABC算法对模型参数进行优化。通过对比分析验证所提出液压泵故障模式识别法的良好性能。

1MSE和MMSE

1.1样本熵

Richman提出的样本熵是一种与近似熵类似的方法，但其在复杂度度量上具有更好的性能，其计算步骤为[4]：

(1) 设原始数据为X={x1,x2,…,xN}，长度为N，预先给定嵌入维数m和相似容限r，考虑m维向量x(i)=[xi,xi+1,…,xi+m-1](i=1,2,…,N-m+1)。

(2) 定义x(i)和x(j)之间的距离d[x(i),x(j)]为两者对应元素差值的最大值，即

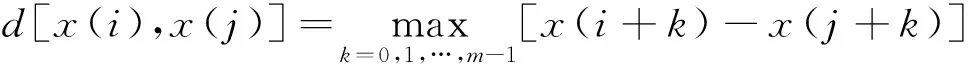
(1)

(i=1,2,…,N-m+1,i≠j)

(2)

(3)

(4)

(6) 该序列的样本熵定义为：

SampEn(m,r,N)=

(5)

SampEn的计算结果受参数m和r的影响很大，同一时间序列采用不同的嵌入维数m和相似容限r求得的样本熵也不同。到目前为止，m和r的取值还没有一个最佳标准，参考相关研究的经验[8]，一般取m=2，r=0.1SD-0.5SD(SD为原始数据的标准差)。本文研究中取m=2，r=0.15SD。

1.2MSE

对于时间序列X={x1,x2,…,xN}，其MSE的计算步骤如下[10]：

(1) 对于时间序列X={x1,x2,…,xN}，长度为N，预先给定嵌入维数m和相似容限r，依据原始序列建立新的粗粒向量为：

(6)

式中：τ=1,2,…,τmax为尺度因子。在尺度因子为τ时，原始序列X被分割成τ个每段长为N/τ的粗粒序列yτ(j)。图1给出了尺度变化示意图。

(2) 对得到的τ个粗粒序列分别求其样本熵，并把它画成尺度因子τ的函数，称之为多尺度熵分析。

样本熵表征的是时间序列在单一尺度上的复杂度和随即程度，熵值越小，序列的自相似性越高，复杂度越低；熵值越大，序列复杂度和随机性越高。MSE定义为时间序列在不同尺度下的样本熵，MSE曲线反映的是时间序列在不同尺度下的复杂度和随机性。

1.3基于MSE的液压泵振动信号分析

实测液压泵振动信号采自液压泵试验台，液压泵型号为SY-10MCY14-1EL，采用型号为Y132M-4的电机驱动，其额定转速为1 480 r/min。选用CA-YD-139型压电式加速度传感器与液压泵端盖进行刚性连接，如图2所示。采集正常、滑靴磨损、松靴和斜盘磨损四种状态液压泵的振动信号各200组，试验中采用装备检修时换下的带故障的柱塞代替正常柱塞的方式模拟故障，振动信号采样频率为50 kHz，采样点数为2 048。试验过程中试验台主溢流阀压力为10 MPa，电机转速为其额定转速。所采集部分液压泵振动信号的时域图和频谱图见图3。

图1　时间序列的粗粒化Fig.1 Coarse-grained procedure of time series

图2　液压泵试验台Fig.2 Test bench of hydraulic pump

图3　液压泵四种状态下的时域波形图和频谱图Fig.3 Time waveform and frequency spectrum of hydraulic pump under four states

由图3分析知，从液压泵振动信号的时域图和频谱图无法有效识别液压泵的状态。因此有必要对液压泵的故障识别方法进行研究。从振动信号中提取出反映液压泵状态的特征信息是实现液压泵故障识别的关键环节。基于MSE算法分析非平稳、非线性信号的良好性能，本节采用MSE算法对液压泵振动信号进行分析。由样本熵的原理知，对样本熵计算结果影响较大的参数有3个：时间序列长度N、嵌入维数m和相似容限r，其中m和r的值根据经验公式求取，但数据长度对样本熵的影响却无经验可循。因此，首先分析长度N对样本熵计算地影响。以液压泵正常状态和斜盘磨损状态下的振动信号为分析对象，为分析N取不同值时样本熵表征液压泵状态的性能，此处所用振动信号的采样点数为20 000。采用以下4种方式对两振动信号进行均分：N=500、N=1 000、N=2 000和N=4 000，这样振动信号序列被分别均分为40段、20段、10段和5段。分别计算每段振动信号序列的样本熵，结果如图4所示。

图4　数据长度对样本熵的影响Fig.4 The influence of data length to sample entropy

对图4进行分析，当N=500时，两种状态下各段数据的样本熵间的差异很大，所得的样本熵曲线波动较大，说明信号序列长度为500时样本熵表征液压泵状态的性能较差；当N=1 000、2 000时，所求得各段信号样本熵曲线相对比较平滑，能够较稳定地表征液压泵状态；当N=4 000时，样本熵曲线更平滑，样本熵表征液压泵状态的性能更好。结果表明：随着序列长度的增加，样本熵表征液压泵状态的性能就更稳定。但是随着时间序列长度的增加，求取每段数据样本熵所需的时间也大大增加，当N=500、1 000、2 000和4 000时计算各段序列样本熵所需时间平均值分别为：0.14 s、2.214 s、5.86 s和21.85 s，程序运行平台为Matlab.7.11.0(R2010b)，计算机主要配置为：2.4 GHz CPU，4 G内存。

另外，从所采集的四种状态下液压泵振动信号中各任取三组，计算每组数据的MSE，结果如图5所示。

图5　液压泵不同状态下的MSEFig.5 MSE of hydraulic pump under different states

对图5进行分析知，当尺度数大于3时，任何尺度下四种状态振动信号的样本熵离散性变强。虽然MSE在多个尺度上都能区分液压泵的不同状态，在尺度较大时，MSE表征液压泵状态的能力降低。针对该问题可以通过增加初始时间序列长度的方式改善，但那样会大大增加运算时间。因此，有必要对MSE算法进行研究，对其算法进行改进，避免时间序列粗粒化造成的时间序列大大缩短的问题。

1.4MMSE

针对尺度较大时MSE表征液压泵状态精度偏低的问题，本节在对MSE算法研究地基础上提出了改进的多尺度熵(Modified Multi-scale Entropy, MMSE)算法，其计算过程为：

(1) 对于时间序列Xi={x1,x2,…,xN}，采用下式实现其粗粒化：

(7)

式中：τ=1,2,…,τmax为尺度因子。根据MSE的经验一般取τmax>10，对于MMSE建议也采用该标准，本文研究中取τmax=20。而当τ=1时，y1(j)即为原时间序列。

(2) 对得到的τ个粗粒化序列分别求其样本熵，即可得到该时间序列的MMSE。

对MMSE原理分析可知，对原时间序列粗粒化实际是以宽度为τ的窗口延时间序列进行滑动，求取窗口内数据的平均值，是一个对原时间序列信息进行提取精简的过程，这样即能够很好地保留原时间序列中的信息，又能够保证时间序列在粗粒化过程中长度不会大幅度缩短。比如当尺度因子为τ时，粗粒化的时间序列长度为N-τ+1，与原时间序列的长度相差很小，从而可以很好地克服MSE因粗粒化而导致的序列长度大大缩短并使其表征状态的能力降低的问题。计算1.3节液压泵四种状态振动信号的MMSE，结果如图6所示。

由图6知，四种状态三组振动信号的MMSE在任何尺度下都具有很好的一致性，MMSE表征液压泵状态的能力基本不随尺度的增加而降低。与图5对比可知，MMSE在任何尺度下都能更好地表征液压泵的状态。基于以上分析，本文采用MMSE作为液压泵的故障特征。

2液压泵故障模式识别策略

2.1模式识别策略

本文研究采用SVM实现液压泵的故障识别，故障识别的策略如图7所示。首先采用MMSE算法对液压泵振动信号进行分析提取故障特征；将提取的特征分为训练特征集和测试特征集，基于训练集采用ABC算法对SVM模型的参数进行优化，基于优化参数建立故障识别模型，测试特征集用于验证所建立模型的性能。

图7　液压泵故障诊断策略 Fig.7 The identification strategy of Hydraulic Pump fault

2.2ABC算法优化的SVM

影响SVM故障识别率的参数主要有核参数g和惩罚系数c。凭借先验知识很难选择它们的最优值，而这两个参数对SVM的学习能力和分类能力影响很大，因此如何准确地选取两个参数是非常关键的问题。本文采用ABC算法对SVM的参数进行优化，其步骤如下：

1) 初始化参数：设置SVM模型的参数搜寻范围，然后在搜寻范围内随机产生20个g和20个c，得到种群数P=20×20的初始蜜源位置；初始化蜂群数量、蜜源被开采次数以及同一蜜源被开采极限；

2) 引领蜂和跟随蜂搜索过程：跟随蜂在当前蜜源附近开展邻域搜索，随机产生新蜜源，如新蜜源的适应度大于原蜜源的适应度，则新蜜源替代原蜜源，迭代次数增加一次，否则保持原蜜源不变；

3) 计算跟随蜂的选择概率：计算蜜源的适应度值，计算跟随蜂选择该蜜源的概率，跟随蜂以概率为依据选择蜜源，搜索产生新的蜜源位置，并计算其适应度，如果适应度值大于原蜜源适应度值，则替代原蜜源，否则保持不变；

4) 判断是否该放弃蜜源：如果蜜源经过一定次数循环后不能被改进，则放弃该蜜源，此处的引领蜂变为侦察蜂，继续寻找新的蜜源将其替代，并记录最优的蜜源；

5) 判断是否满足最大迭代次数，若没有，转到步骤2)继续执行；若满足，则输出最优解，停止搜索，程序结束。

3实验验证

从1.3节采集的四种状态液压泵振动信号中各任意选取70组作为样本集，其中每种状态的前30组为训练集、后40组为测试集，提取振动信号的MMSE作为故障特征，采用SVM算法实现液压泵的故障状态识别。首先定义液压泵的分类标签，分类标签如表1所示；然后计算训练集中120组样本的MMSE，此处MMSE的尺度因子为20，所求得120组训练样本的MMSE如8图所示。图8中每条曲线表示120个样本在相同时间尺度下的样本熵。可以看出，在任何尺度下MMSE都能有效将液压泵的四种状态有效区分。同一状态下同一样本的MMSE随着尺度的增加而降低。

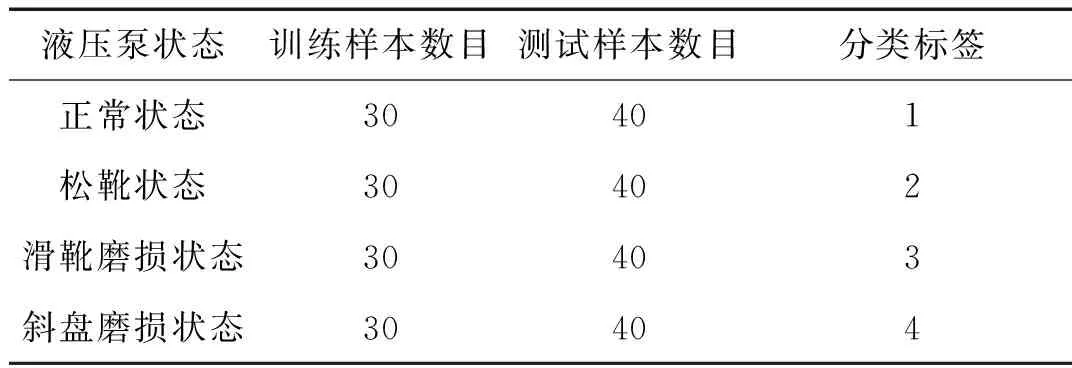
表1　识别标签

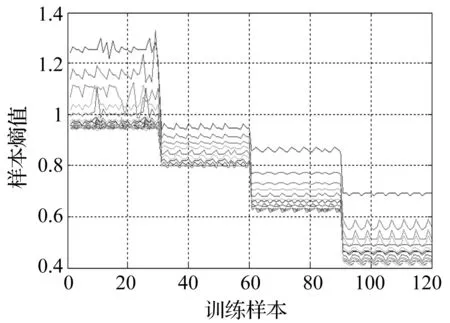
图8　训练样本的MMSEFig.8 MMSE of training samples

不同样本的MMSE就是一个20维的特征向量，由此得到了120×20的训练特征集；基于训练特征集，分别采用ABC算法、粒子群优化算法(Particle Swarm Optimization algorithm, PSO)和遗传算法(Genetic Algorithm, GA)对SVM的模型参数c和g进行寻优，三种算法的主要参数设置如表2所示。三种算法寻优过程中适应度变化曲线如图9所示，寻优结果如表3所示。从图9可以看出，在训练特征集相同的条件下，ABC算法与其它两种算法相比，能够更快地搜寻到全局最优解，并且状态识别率更高。

表2　三种优化算法参数设置

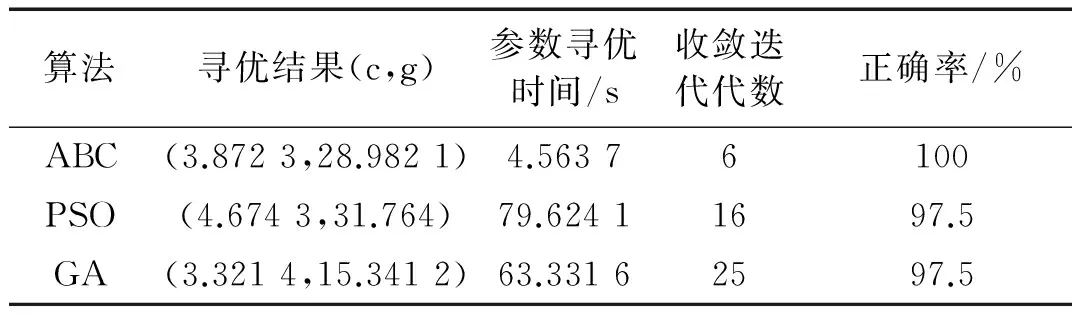
表3　三种优化算法优化结果对比

图9　三种寻优算法适应度曲线Fig.9 Adaption curves of three optimizing algorithms

基于优化参数和训练特征集分别建立ABCSVM模型、PSOSVM模型和GASVM模型。求取测试集每个样本的MMSE得到测试特征集，并采用所建立的模型对训练特征集和测试特征集进行模式识别，识别结果见图10。

从图10中可以看出，对训练特征集进行故障模式识别，三种模型的正确识别率都达到了100%。对测试特真集进行故障模式识别，ABCSVM模型的识别率为98.75%，GASVM模型的正确识别率为91.875%，PSOSVM模型的正确识别率最低，为90.625%。

通过对比分析可以得出以下结论：ABC优化算法可以准确快速的搜索到g和c的最优值，基于该参数组建立的故障识别SVM模型的故障识别率更高，结果验证了所提出ABCSVM算法的有效性和良好性能。

图10　三种模型的识别结果Fig.10 Identification results with three different models

4结论

(1)在对MSE算法研究的基础上提出了MMSE算法，通过对液压泵实测信号分析验证了所提出的MMSE能有效的解决MSE算法计算过程中在尺度较大时其表征液压泵状态性能较差的问题。

(2)为了提高液压泵的故障识别率，采用ABC算法对SVM模型的参数进行优化。采用液压泵四种状态下振动信号的MMSE作为特征向量，利用ABCSVM模型实现液压泵的故障模式识别，结果验证了该方法的良好性能。

(3)基于相同的特征集，采用PSOSVM模型与GASVM模型对液压泵的故障状态进行识别，结果表明所提出的ABCSVM算法具有更高的识别效率和准确率。

参 考 文 献

[1] Dong Shao-jiang,Tang Bao-ping,Chen Ren-xing. Bearing running state recongnition based on non-extensive wavelet feature scale entropy and support vetor machine[J].Measurement,2013,19(46):4186-4199.

[2] 王冰,李洪儒,许葆华.基于数学形态学分段分形维数的电机滚动轴承故障模式识别[J].振动与冲击,2013,32(19):28-31.

WANG Bing,LI Hong-ru,XU Bao-hua.Fault pattern recognition for electromotor rolling bearing based on mathematical morphology sectionalized fractal dimension[J]. Journal of Vibration and Shock,2013,32(19):28-31.

[3] 白蕾,梁平.基于小波包滤波的汽轮机转子振动故障的Kolmogorov熵诊断[J].振动与冲击，2008,27(5),148-152.

BAI Lei,LIANG Ping. Kolmogorov entropy diagnosis for vibration faults of turbine rotor based on wavelet packet filtering[J]. Journal of Vibration and Shock,2008,27(5):148-152.

[4] Richman J S,Moorman J R. Physiological time-series analysis using approximate and sample entropy[J]. American Journal of Physiology Heart Circulatory Physiology,2000,43(278):2039-2049.

[5] Cabal-Yepez E,Romero-Troncoso R J,Garcia-Rerez A,et al. Single-parameter fault identification through information entropy analysis at the startup transient current in induction motors[J]. Electric Power Systems Research,2012,32(89):64-69.

[6] 李娜,方彦军.利用关联维数分析机械系统故障信号[J].振动与冲击,2007,26(4):136-139.

LI Na,FANG Yan-jun. Fault signal analysis of mechanical system based on correlation dimension[J]. Journal of Vibration and Shock,2007,26(4):136-139.

[7] Yentes J M,Hunt N,Schmid K K,et al. The appropriate use of approximate entropy and sample entropy with short data sets[J]. Annals of Biomedical Engineering,2013,41(2):349-365.

[8] 赵志宏,杨绍普.一种基于样本熵的轴承故障诊断方法[J].振动与冲击,2012,31(6):136-140.

ZHAO Zhi-hong,YANG Shao-pu. Sample entropy-based roller bearing fault diagnosis method[J]. Journal of Vibration and Shock,2012,32 (6):136-140.

[9] 张毅,罗明伟,罗元.脑电信号的小波变换和样本熵特征提取[J].智能系统学报,2012,7(4):1-6.

ZHANG Yi,LUO Ming-wei,LUO Yuan. EEG feature extraction method based on wavelet transform and sample entropy[J]. CAAI Transactions on Intelligent Systems,2012,7(4):1-6.

[10] Costa M,Goldberger A L,Peng C K. Multiscale entropy analysis of biological signals[J]. Physical Review E,2005,26(71):1-18.

[11] Begum S,Barua S,Filla R,et al. Classification of physiological signals for wheel loader operators using Multi-scale Entropy analysis and case-based reasoning[J]. Expert Systems with Applications,2014(41):295-305.

[12] Zhang Long,Xiong Guo-liang,Liu He-sheng,et al. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference[J]. Expert Systems with Applications,2010(37):6077-6085.

[13] Zhu Ke-heng,Song Xi-geng,Xue Dong-xin. A roller bearing fault diagnosis method based on hierarchical entropy and support vector machine with particle swarm optimization algorithm[J]. Measurement,2014(47):669-675.

[14] Li Ning,Zhou Rui,Hu Qing-hua,et al. Mechanical fault diagnosis based on redundant second generation wavelet packet transform,neighborhood rough set and support vector machine[J]. Mechanical Systems and Signal Processing,2012(28):608-621.

[15] 姜万录，吴胜强. 基于SVM和证据理论的多数据融合故障诊断方法[J]. 仪器仪表学报,2010,31(8):1738-1743.

JIANG Wan-lu,WU Sheng-qiang. Multi-data fusion diagnosis method based on SVM and evidence theory[J]. Chinese Journal of Scientific Instrument,2010,31(8):1738-1743.

Fault pattern recognition of hydraulic pumps based on MMSE and ABCSVM

LI Hong-ru1, WANG Yu-kui1,2, MA Ji-qiao1, YE Peng1

(1. Ordnance Engineering College, Shijiazhuang 050003, China; 2. Air Force Logistics College, Xuzhou 021000, China)

Abstract:In order to realize fault pattern recognition of hydraulic pumps, the methods of fault feature extraction and pattern recognition were studied. Aiming at the bad performance of large scale sample entropy to reflect the state of pumps when the scale factor of multi-scale sample entropy (MSE) was larger and then the length of time series was shorter, the modified multi-scale entropy (MMSE) was proposed here. The results obtained by adopting MMSE to analyze practical signals of pumps testified MMSE’s favorable performance. Considering the nonlinear relationship between pump fault pattern and fault features, a support vector machine (SVM) was used to realize the fault pattern recognition of pumps, and the artificial bee colony (ABC) algorithm was proposed to optimize the parameters of the SVM model. The fault pattern recognition of pumps was realized based on MMSE and ABCSVM, the favorable performance of the proposed method was demonstrated with comparison and analysis.

Key words:hydraulic pump; pattern recognition; MMSE; artificial bee colony algorithm; SVM

基金项目：国家自然科学基金(51275524)

收稿日期：2014-12-31修改稿收到日期：2015-05-11

中图分类号:TH322；TP306+.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.024

第一作者 李洪儒 男，教授,博士生导师，1963年1月生