基于小波模极大值模糊熵的遥测振动信号异常检测

刘　学， 梁　红， 玄志武

(中国人民解放军91550部队94分队，辽宁 大连　116023)

基于小波模极大值模糊熵的遥测振动信号异常检测

刘学， 梁红， 玄志武

(中国人民解放军91550部队94分队，辽宁 大连116023)

摘要：针对遥测振动信号频域成份复杂、非平稳非线性和强噪声特性，提出一种基于小波模极大值模糊熵的遥测振动信号异常检测方法。首先对采集到的遥测振动信号进行零漂修正和趋势项消除；然后对经预处理后的振动信号进行一维连续小波变换，计算所有尺度空间中的小波模极大值序列；最后将原信号及其小波模极大值序列的模糊熵构成的特征向量输入到SVM分类器，根据模糊熵的变化情况对遥测振动信号进行异常检测。实测数据验证了该方法的有效性。

关键词：遥测振动信号；小波模极大值；模糊熵；支持向量机；异常检测

遥测振动信号为典型的非平稳信号，叠加大量的高频、低频和冲击噪声，当飞行器在飞行过程中发生异常或故障，振动信号中还将夹杂着各阶次的瞬态谐波分量，且相互之间存在非线性耦合关系，频域成分异常复杂。传统的遥测振动信号的异常分析主要表现其时域或频域的特征，如傅氏谱、功率谱和冲击谱等，表征的特征信息过于单一。时频分析技术可以提供时间域与频率域的联合分布信息[1-2]，但遥测振动信号频域成分异常复杂以及大量噪声的存在使得时频分析方法产生严重的模态混叠现象，很难分解出纯净的单分量信号,这就造成时频能量分布覆盖整个时频平面，难以解读，为遥测振动信号进行分析和异常检测带来困难。

非线性动力学中的混沌序列复杂度测度算法从时间序列复杂度的角度来度量信号产生新模式的概率大小，为时间序列的复杂性和统计量化提供了一种新的度量方法，在表征信号动力学特征方面较关联维数包含更多的特征信息，目前序列复杂度测度算法主要包括近似熵( Approximate Entropy, ApEn)算法[3]和样本熵(Sample Entropy, SampEn)算法[4]，它们均采用Heaviside函数作为相似性度量函数，作为对近似熵算法的改进，样本熵算法不计算与自身匹配的统计量，只对产生的新信息进行测度，但在无模板匹配的情况下会出现无意义的In0，但它们共同的缺陷就是对相似容限、相空间维数和序列长度的取值非常敏感，为此，文献[5-6]在对肌电信号特征提取时提出了模糊熵(Fuzzy Entropy, FuzzyEn)算法，验证了该算法对肌电信号复杂度分析的有效性。文献[7]将模糊熵算法与近似熵和样本熵算法作对比分析，证明模糊熵算法对相空间维数和相似容限度的敏感性、依赖性更低，鲁棒性和测度值的连续性更好。

本文将非线性动力学理论引入到对遥测信号异常检测中，提出一种基于小波模极大值模糊熵的遥测振动信号异常检测方法，通过提取信号的小波模极大值的模糊熵作为特征向量可以更为细致地捕获到遥测振动信号的非平稳程度以及信号在不同尺度下动态变化的复杂度，同时采用SVM分类器对振动信号的状态进行分类，有效的解决了小样本条件下振动信号的异常检测问题。

1小波模极大值

对于有限能量信1号f(t)∈L2(R)，L2(R)为能量有限的信号空间，其一维连续小波变换为

(1)

2模糊熵算法

模糊熵衡量非线性序列新模式产生的概率大小，测度值越大，表征新模式产生的概率越大，较近似熵和样本熵算法对相空间维数和相似容限度的敏感性、依赖性更低，鲁棒性和测度值的连续性更好。对信号来说，模糊熵表征信号的非平稳程度，模糊熵越大其频率成分越丰富，复杂度越高；而模糊熵越低则表示信号越趋于周期性、频谱越窄。因此本文选择模糊熵算法提取遥测振动信号小波模极大值序列的特征参数,算法流程如下:

ym[i]={xi,xi+1,…,xi+m-1}-y0(i)

(2)

(3)

其中m为相空间维数，i=1,2,…,N-m+1。

(2) 定义模糊隶属函数为

(4)

(5)

得到相空间不同维之间的模糊度为

(6)

(7)

(4) 令相空间维数为m+1,重复(1)～(3)步，得到该序列的模糊熵为

FuzzyEn(m,r,N)=lnΦm(r)-lnΦm+1(r)

(8)

式中，参数m,r,N分别为相空间维数、相似容限度、非线性序列长度，m表征非线性系统所拓展的相空间维度的大小，m的选择直接关系能否精确的重构系统的动态演化过程。相似容限r的选择关系到FuzzyEn(m,r,N)的计算精度，如果取值过大将对导致时间序列包含信息的丢失，而取值太小则会增加FuzzyEn(m,r,N)计算结果对噪声的敏感性。在后面的实验中，本文将对FuzzyEn算法在不同的相空间维数m和相似容限r条件下与ApEn和SampEn算法的性能作对比测试，分析各算法性能并确定m和r的取值。

3基于小波模极大值-FuzzyEn的遥测振动信号异常检测方法

当采集到的遥测振动信号出现异常时，其频率成份和分布会发生变化，相应的模糊熵也会发生改变，但在某些情况下仅采用原信号的模糊熵测度不能反应信号变化的细节，而小波模极大值序列反应了信号的突变点信息，且遥测振动信号的异常一般都对应于信号的突变点，因此可计算尺度空间中振动信号小波模极大值的模糊熵，通过尺度空间中模糊熵的分布以及变化情况可以更为细致的表征信号的非平稳程度和动态演化过程。异常检测流程如下：

(1) 首先对采集到的遥测振动信号进行零漂修正和趋势项消除，然后对经预处理后的振动信号进行一维连续小波变换，为了突出不同时刻的小波模极大值，采用具有较好的时域局部分辨率的样条小波dB3作为基小波来进行小波变换；

(2) 将小波变换后所有尺度空间中的模极大值点按时间进行组合得到小波模极大值序列；

(3) 采用式(2)～(8)计算各样本及其小波模极大值序列的模糊熵FuzzyEn(m,r,N)；

(4) 利用各样本及其小波模极大值序列的模糊熵FuzzyEn(m,r,N)构建特征向量；

(5) 将第(4)步构建的模糊熵特征向量作为训练样本输入SVM分类器进行训练，SVM的核函数采用径向基核函数(RBF)，采用n-fold cross validation法[9]对RBF的两个参数Gamma和惩罚因子C进行选取；

(6) 将测试样本的特征向量输入到SVM分类器，通过分类器的输出值对遥测振动信号进行异常检测，如输出值为1表示信号正常，否则为异常。

4实测数据分析

实验1：FuzzyEn算法在不同的相空间维数m和相似容限r条件下与ApEn和SampEn算法的性能作对比测试：

(1)r=0.25×SD时，采用不同的m对ApEn、SampEn和FuzzyEn算法性能进行测试；

(2)m=2时，采用不同的r对ApEn、SampEn和FuzzyEn算法性能进行测试；

SD为振动信号时间序列的标准差，测试信号采用某次试验任务采集的遥测高频振动信号，信号长度N=1 192，采样频率为5 kHz，实验结果见图1。

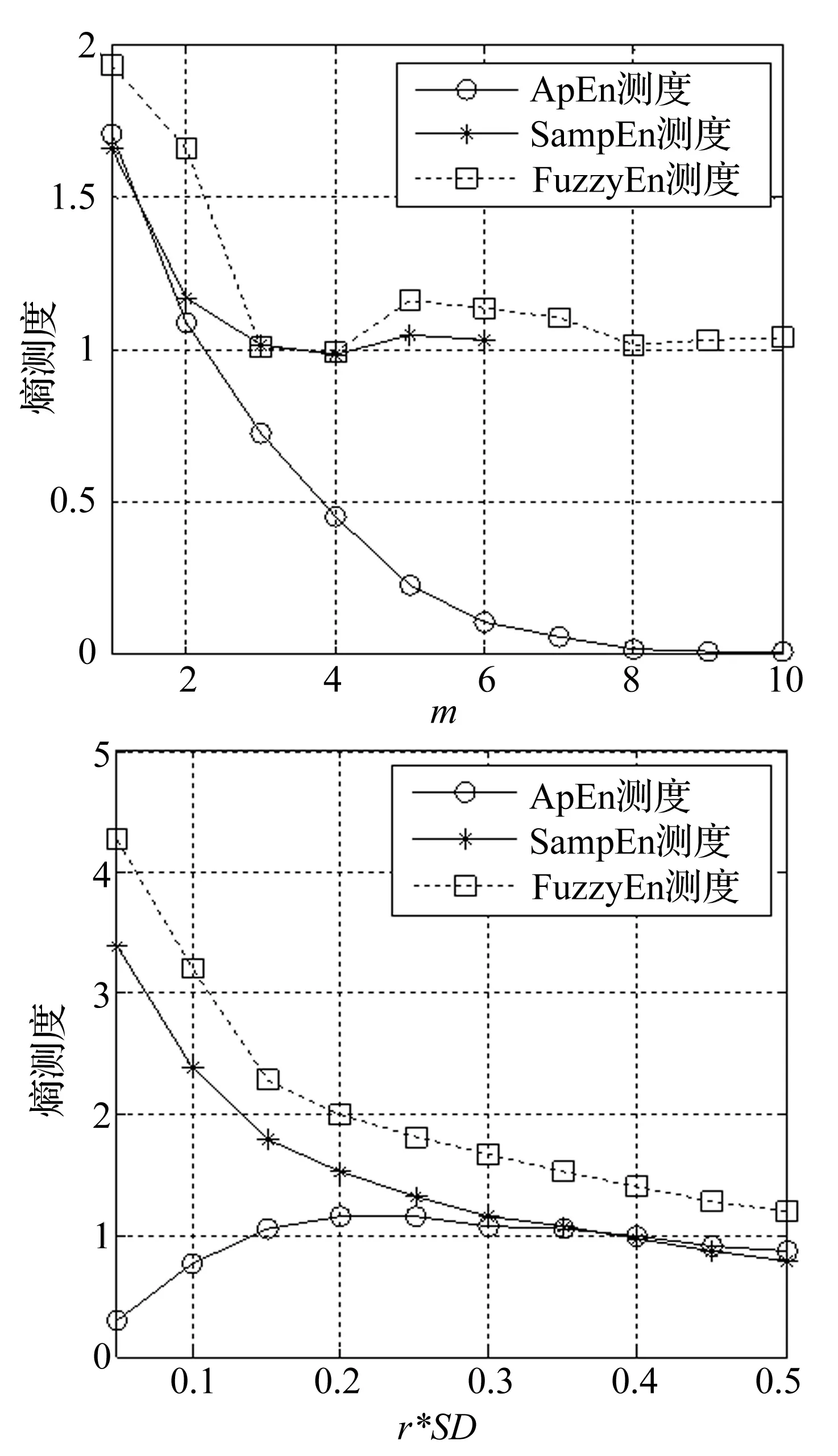
图1　FuzzyEn算法对比ApEn和SampEn算法性能测试Fig.1 Performance comparison results of FuzzyEn, ApEn and SampEn algorithm

从图1可见，ApEn算法只在m≤2，r≥0.2×SD时有效，当m≥3或r<0.2×SD时即出现错误的测度值，由此可见ApEn算法对m和r的取值最为敏感；SampEn算法的性能较ApEn算法有所提高，但连续性和稳定性差，当m>6时SampEn算法的熵测度值出现无意义的ln0的情况，导致算法不连续，稳定性较差，但对r的取值不敏感；FuzzyEn算法熵测度值随着m和r的增大逐渐趋于稳定，当m=10时仍能对信号的复杂度进行测量，敏感性、依赖性方面优于ApEn和SampEn算法。根据图1的实验结果，当m=2或3时，FuzzyEn算法对信号复杂度的变化更敏感，且计算量适中，由于r的取值直接关系到熵测度的计算精度和信号信息的完整性，取值不宜过大，从实验结果看r的取值在[0.250.35]范围内较为合适，对于信号长度的取值，文献[7]经研究发现，N的取值在[1005 000]范围内可以得到较为准确的熵测度。

实验2：为验证文中提出方法的有效性，对只采用原信号FuzzyEn作为特征值与采用小波模极大值-FuzzyEn特征向量的遥测振动信号异常检测方法的性能进行对比测试，采用某型飞行器12次飞行试验同一位置的传感器采集的遥测振动信号样本进行处理验证。采样频率为5 kHz，m=2，r=0.3×SD，N=2 048，其中某一故障样本的时域波形及其一维连续小波变换见图2。

本文采用具有较好的时域局部分辨率的样条小波dB3作为基小波来进行小波变换，将各遥测振动信号样本分解为8层，按照第2节给出的小波模极大值的定义，计算各层的小波模极大值序列见图3。各样本及其小波分解后各层小波模极大值序列的模糊熵FuzzyEn(m,r,N)见表1。(限于篇幅，表中只给出FuzzyEn(m,r,N)变化相对较为明显的1、2、4、6层的小波模极大值序列的模糊熵值)。随机抽取3个正常信号和4个异常信号样本的FuzzyEn特征值和小波模极大值-FuzzyEn特征向量分别作为训练样本输入到SVM分类器进行训练，经过实验当RBF核函数的两个参数Gamma=2.1，C=1.7时SVM分类准确率最高。剩余的5个样本的特征向量作为测试样本进行异常检测，异常检测结果见图4。

从图4可以看出，仅采用原信号的FuzzyEn作为特征值的异常检测方法在对测试样本7和11进行分类是出现错误，从表1中原信号的模糊熵值可以看出，各样本的FuzzyEn(m,r,N)值相互重叠，因此采用原始遥测振动信号模糊熵作为特征值是不能对振动信号异常进行准确检测的。而基于小波模极大值-FuzzyEn特征向量的异常检测方法对所有测试样本均作出了正确的分类，在小样本的情况下异常检测准确率达到了100%，因此可以得出结论：该方法可以更为细致的对信号非平稳程度和动态变化情况进行检测。

实验3：仍采用实验2的样本，对基于小波模极大值-FuzzyEn的遥测振动信号异常检测方法在小样本情况下SVM与BP神经网络和模糊C均值聚类分类器的性能对比测试，实验结果见表2。

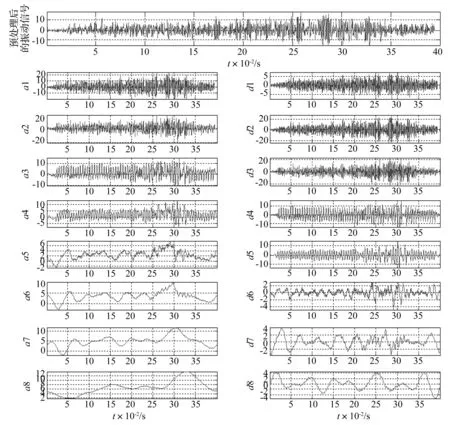
图2　预处理后遥测振动信号及其一维连续小波变换Fig.2 The preprocessed telemetry vibration signal and its one-dimensional continuous wavelet transform

样本序号系统状态模糊熵(FuzzyEn)原信号1层模极大值序列2层模极大值序列4层模极大值序列6层模极大值序列12345统计正常0.79170.63250.87290.77010.64990.7434±0.10116.18096.21306.26216.17396.23136.2122±0.03645.89186.15056.17725.87136.09556.0373±0.14531.91801.94001.91561.90031.93361.9215±0.01571.00971.03931.03180.99251.02591.0198±0.01886789101112统计量故障1.65981.08570.79360.81341.38890.76590.81281.0457±0.35272.61622.24382.71416.06533.62543.49225.92993.8124±1.570311.296414.643613.49829.129815.188211.33479.353212.0634±2.43423.21733.46711.83282.99312.69551.93382.06442.6006±0.66031.62221.69671.13771.50011.96541.05231.00381.4255±0.3673

表2异常检测分类器性能对比结果

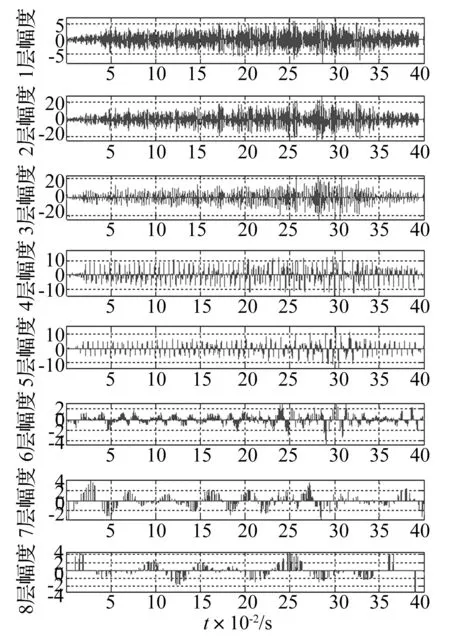
图3　实测遥测振动信号小波模极大值序列Fig.3 Wavelet modulus maxima sequence of measured telemetry vibration signal

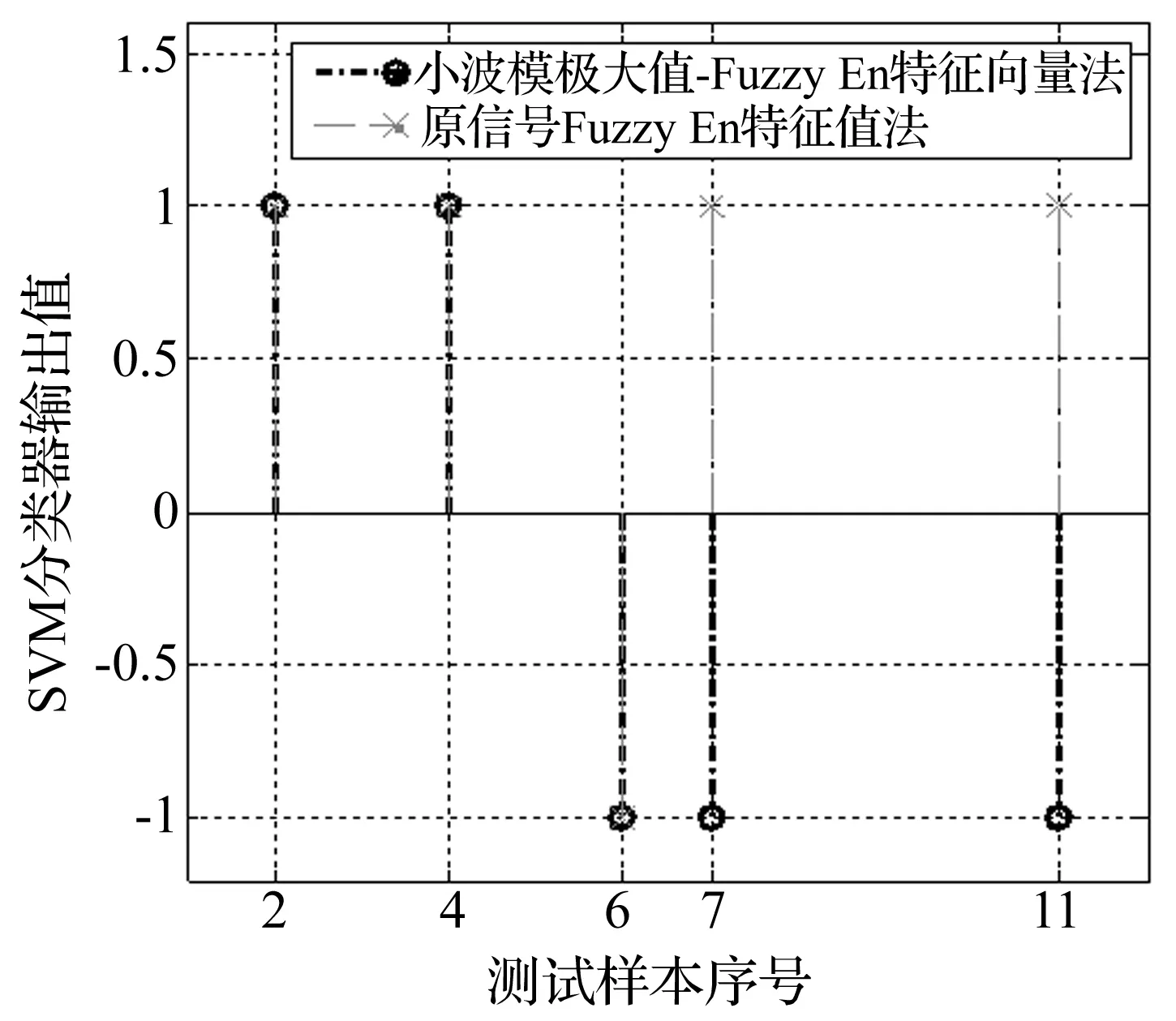
图4　异常检测方法性能对比Fig.4 Performance comparison between the anomaly detection method

由于飞行器试验难度较高且成本高昂，试验次数较少导致的采集的样本数量较小，这就对遥测振动信号进行异常检测带来了困难，目前大多数的分类器都需要采用大量的样本进行训练才可以获得准确的分类模型，如何在小样本的条件下进行准确的分类是本研究必须考虑的内容，从表2可以看出，在12组振动信号小样本的条件下，综合分类精度和训练时间，SVM分类器的性能优于BP神经网络和模糊C均值聚类分类器。在小样本条件下仍能稳健准确的对信号的异常进行辨识。

5结论

提出一种基于小波模极大值-FuzzyEn的遥测振动信号异常检测方法，依据小波模极大值和模糊熵理论，采用小波变换系数模的过零点和局部极值点更能体现信号的突变以及动态变化情况，因此小波模极大值的模糊熵可以更为细致地捕获到遥测振动信号的非平稳程度以及在不同尺度下动态变化的复杂度，同时采用SVM分类器对振动信号的状态进行分类，有效的解决了小样本条件下振动信号的异常检测问题。实测信号的分析结果表明该方法能够有效地运用于遥测速变信号的异常检测，同时亦可以推广到其他异常检测和故障辨识领域。

参 考 文 献

[1] 程军圣，张亢，杨宇，等．局部均值分解与经验模式分解的对比研究[J]． 振动与冲击，2009，28(5):13 -16．

CHENG Jun-sheng,ZHANG Kang,YANG Yu,et al. Comparison between the methods of local mean decomposition and empirical mode decomposition[J]．Journal of Vibration and Shock，2009，28(5):13 -16．

[2] 杨德昌，唐巍，屈瑞谦，等．基于改进局部均值分解的低频振荡参数提取[J]．中国电机工程学报，2013，33(4)：135-140．

YANG De-chang,TANG Wei,QU Rui-qian,et al. Extraction of the oscillatory parameters of low frequency oscillation based on improved local mean decomposition[J]．Proceedings of the CSEE，2013，33(4)：135-140．

[3] 黄林洲，郭兴明，丁晓蓉．EMD近似熵结合支持向量机的心音信号识别研究[J]．振动与冲击，2012，31(19):21-25．

HUANG Lin-zhou,GUO Xing-ming,DING Xiao-rong. Heart sound recognition based on EMD approximate entropy and SVM[J]．Journal of Vibration and Shock，2012，31(19):21-25．

[4] 张学清，梁军．基于EEMD一近似熵和储备池的风电功率混沌时间序列预测模型[J]. 物理学报,2013,62 (5):050505-1-9.

ZHANG Xue-qing,LIANG Jun. Chaotic time series prediction model of wind power based on ensemble empirical mode decomposition-approximate entropy and reservoir[J]. Acta Physica Sinica,2013,62(5):050505-1-9.

[5] Chen W T,Wang Z Z,Xie H B,et al. Characterization of surface EMG signal based on fuzzy entropy[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering,2007,15:266-272.

[6] Costa M，Goldberger A L,Peng C K . Multiscale entropy analysis of biological signals[J].Physical Review F，2005，71:021906.

[7] 孙克辉，贺少波，尹林子，等．模糊熵算法在混沌序列复杂度分析中的应用[J]. 物理学报,2012,61(13):130507-1-7.SUN Ke-hui,HE Shao-bo,YIN Lin-zi,et al. Application of Fuzzy En algorithm to the analysis of complexity of chaotic sequence[J]. Acta Physica Sinica,2012,61(13):130507-1-7.

[8] Gao X T,Bacry E,Sattar F,et al. Multiscale contour corner detection based on local natural scale and wavelet transform[J]. Image and Vision Computing,2007,25 (6):890-898．

[9] 李峰，汤宝平，章国稳．基于舍一交叉验证优化最小二乘支持向量机的故障诊断模型[J]．振动与冲击，2010,29(9):170-174.

LI Feng,TANG Bao-ping,ZHANG Guo-wen. Fault diagnosis model based on least square support vector machine optimized by leave-one-out cross-validation[J]．Journal of Vibration and Shock,2010,29(9):170-174.

Telemetry vibration signal anomaly detection method based on fuzzy entropy of wavelet modulus maxima

LIU Xue, LIANG Hong, XUAN Zhi-wu

(94Unit, Troop 91550, PLA, Dalian 116023, China)

Abstract:Aiming at telemetry vibration signals in frequency domain with characteristics of complex components, nonlinearlty and non-stationeriness, and strong noise, a telemetry vibration signal anomaly detection method based on fuzzy entropy of wavelet modulus maxima was proposed. Firstly, collected telemetry vibration signals were modified with zero-drift and their trend terms were eliminated. Secondly, the one-dimensional continuous wavelet transformation was used to convert the preprocessed vibration signals, and then all scale spaces’ wavelet modulus maxima sequences calculated. Finally, the feature vectors formed with the fuzzy entropy of the original signal and its wavelet modulus maxima sequence was input into a SVM classifier, then the abnormal telemetry vibration signal was detected according to changes of fuzzy entropy. The measured data demonstrated the effectiveness of this method.

Key words:telemetry vibration signal; wavelet modulus maxima; fuzzy entropy; SVM; anomaly detection

收稿日期：2015-03-09修改稿收到日期：2015-05-02

中图分类号:TN911.7

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.023

第一作者 刘学 男，博士，高级工程师，1983年10月生