敷设主动约束层阻尼圆锥壳的控制特性分析

陆　静, 袁丽芸

(广西科技大学 汽车与交通学院,广西 柳州　545006)

敷设主动约束层阻尼圆锥壳的控制特性分析

陆静, 袁丽芸

(广西科技大学 汽车与交通学院,广西 柳州545006)

摘要：基于压电材料的本构关系和内力位移方程，考虑压电材料的正、逆压电效应，求出了压电约束层的动力学控制方程和电学控制方程。根据圆锥壳的几何特性，将变量沿周向进行傅里叶展开，可将上述方程转化为沿母线方向的一阶常微分方程的形式。结合黏弹层的法向平衡方程和位移连续性条件，由主动约束层和基壳的力学方程导出层合结构的动力学方程，并将该方程与压电约束层的电学方程联立，建立了敷设主动约束层圆锥壳的机电耦合模型。然后，借助精细积分技术和叠加原理，采用速度反馈控制策略，提出了一种分析此类结构的半解析、半数值方法，并采用该方法分析了反馈系数、反馈点的布置等参数对敷设主动约束层阻尼圆锥壳振动特性和控制特性的影响。

关键词：主动约束层阻尼；圆锥壳；速度反馈控制策略；机电耦合；控制特性

约束层阻尼(Constrained Layer Damping，CLD)结构由基体、黏弹层和约束层组成，当基体材料振动时，由于约束层的作用，可以进一步增加黏弹性层的剪切耗能的作用，显著降低结构共振峰值，具有更明显的减振效果。如果约束层材料为智能材料，则称该结构为主动约束层阻尼(Active Constrained Layer Damp，ACLD)。主动约束层阻尼技术是一种具有典型智能结构特征的主/被动一体化振动控制技术，它同时具备被动控制安全可靠和主动控制自适应性强、控制效率高的优点，可以在较宽频带上获得很好的阻尼特性，具有优越的减振降噪控制效果。目前，对于ACLD结构多采用有限元法。Biswas等[1]采用一阶剪切理论和非线性的本构关系，建立了ACLD梁有限元模型，讨论了结构的非线性振动特性，及其结构参数对减振效果的影响。Vasques[2]利用层合理论提出了一种书本式ACLD结构梁的有限元模型。Ray等[3-4]对ACLD梁、板、壳等结构的有限元建模和阻尼特性等进行了详细的研究，获得了一系列的研究成果。但是，由于存在网格划分，有限元法在高频段内的计算精度很差，且当结构参数改变时，有限元法需要重新建模和分析，计算效率不高。解析法具有很高的精度，但它仅适用于简单的结构，适用范围较小。因此，一些学者提出了分析CLD结构的半解析方法。李恩奇等[5-6]采用能量原理，建立了敷设被动约束层阻尼板和圆柱壳的动力学模型，提出了一种分析CLD结构动力学特性的传递矩阵法。由于状态向量不含内力分量，因此，他们的方法很难用于ACLD结构的建模。袁丽芸等[7]基于线黏弹性理论和层间的连续性条件，导出了敷设ACLD圆柱壳的一阶控制方程，并提出了一种新的模态控制方法，取得了较好的减振效果。锥壳在工程中的应用非常广泛，许多工程结构都可简化成锥壳或锥—柱结合壳。通过在圆锥壳表面敷设ACLD结构，可以达到较好的减振降噪效果。因此，研究ACLD圆锥壳的振动及阻尼特性具有重要的现实意义。由于几何特性比圆柱壳更为复杂，目前对于ACLD圆锥壳的研究较少。Kumar等[8]利用Hamilton原理建立了敷设ACLD块的圆锥壳有限元模型，分析了敷设位置对减振性能的影响。陆静等[9]基于板壳理论和层合理论，导出了被动约束层阻尼(Passive Constrained Layer Damp，PCLD)圆锥壳的数学模型。在此基础上，通过引入压电材料的膜内力，本文建立了ACLD圆锥壳的机电耦合模型，并借助叠加原理，提出了一种分析ACLD圆锥壳动力学特性的半解析方法。

1压电约束层的电学控制方程

图1　ACLD圆锥壳的横截面简图Fig.1 Cross-sectional schematic of an ACLD conical shell

ACLD圆锥壳由基壳、黏弹层和压电约束层组成，在文中分别用1、2、3表示，截面图如图1所示，图中x,z分别表示母线方向和法向，圆周方向用θ表示，α为半锥角，R01、R02、R03分别表示各层的中面半径。为了方便推导，做以下假设[10]：① 基壳、黏弹层和压电约束层沿法向的位移w相同；② 各层之间层间位移连续；③ 只考虑黏弹层的剪切变形和考虑法向振动惯量，面内惯性忽略不计。同时，对电场强度作以下假设：① 母线方向和周向的电场强度Es和Eθ与z无关；② 法向的电场强度Ez与x、θ无关，且在厚度方向均匀分布，即Ez=V/h3，其中V为驱动电压，h3为压电约束层的厚度。

压电约束层的材料为沿z方向极化的横观各向同性材料，将压电约束层看成薄壳结构，由压电材料的三维本构方程退化得到压电约束层的物理方程和电学方程

(1)

Dx=∈11Ex,Dθ=∈22Eθ

Dz=e31εx+e32εθ+∈33Ez

(2)

(3)

式中，Φ为电势函数，由电场强度的假设(2)可得

(4)

式中，f(x,θ)为压电约束层中面的电势分布。

将式(4)代入式(3)，可得

(5)

自然坐标系下，压电圆锥壳的电学方程为：

(6)

根据薄壳理论，壳体内任一点的应变可以表示为

(7)

结合式(2)、式(5)和式(7)，可将式(6)写为

(8)

将χx和χθ的表达式代入式(8)，并对方程变量沿周向进行傅里叶展开和无量纲化处理，即令

,

(9)

文中带“-”上标的变量表示无量纲化后的幅值。

对式(5)第一式也进行同样的处理，可得

(10)

式(9)和式(10)即为压电约束层的电学补充方程，该方程同时考虑了电学量和力学量的影响，为一组机电耦合的方程，且由于考虑了3个方向电场强度的影响，具有较高的精度。

2ACLD圆锥壳的动力学模型

由式(1)积分可得压电约束层内的膜内力

(11)

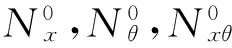
(12)

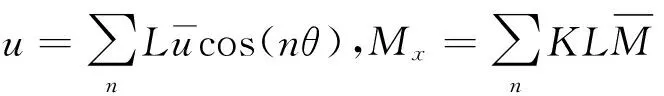
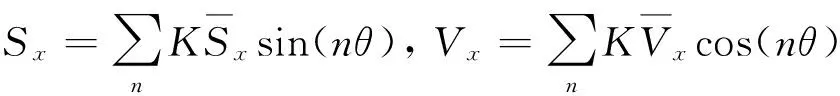
(13)

在压电约束层采用速度反馈控制策略，谐激励作用下，压电约束层的驱动电压可以写为

V(ω)=-(iω)kdw(ξ0,θ0)

(14)

式中，kd为速度增益系数，w(ξ0,θ0)为反馈点的法向位移，ω为激励的频率。

将(14)式代入(5)式第三式，求出?Ez后代入(11)式的相关表达式后可得

(15)

由式(13)可求出基壳动力学控制方程

(16)

由于在式(13)和式(16)的载荷向量中均包含未知的层间相互作用力，本文参照文献[9]的方法，将未知量消去，整合出了ACLD圆锥壳的整体控制方程。限于篇幅，仅列出简单的推导过程。

由壳体的假设式(3)可列出黏弹层的法向平衡方程

(17)

仅考虑黏弹层的切应变，由一阶剪切变形理论可求出中面的切应力幅值为

(18)

式中，Ti(i=1～6)为与几何参数有关的系数，表达式详见文献[9]。

考虑剪切力的作用及其偏心的影响，式(13)和式(16)的载荷可以写为

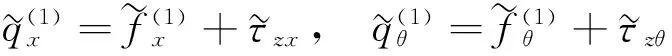
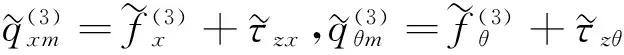
(19)

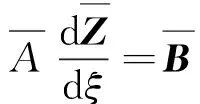
(20)

式中，整合状态向量为

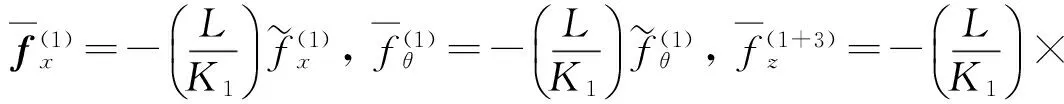
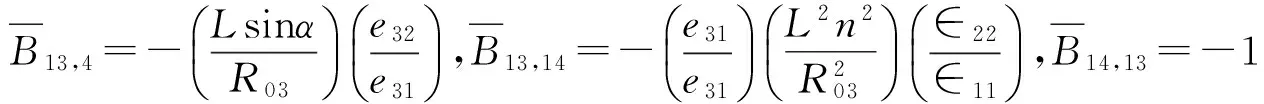
3数值计算方法

由式(20)可以看出，在压电载荷向量中包含未知的反馈点位移w(ξ0,θ0)，该方程为耦合方程，很难直接求解。本文基于齐次扩容精细积分法和叠加原理，提出了一种求解此类耦合方程的半解析方法。

(21)

式中，Hi为状态向量之间的传递矩阵，Qi为载荷向量所引起的非齐次项。

将圆锥壳分成n段，在每段内均可求出与式(21)类似的传递关系，因此可得到14n个代数方程，在壳的边界上有14个边界条件，将上述代数方程组装成一个矩阵方程

MI=J

(22)

(23)

令ξ=ξ0,θ=θ0，则可求出反馈点的位移

(24)

将求出的w(ξ0,θ0)代入式(20)，则方程的非齐次项均为已知量，再次运用齐次扩容精细法，由式(23)即可求出ACLD旋转壳上任意点的状态向量，进而分析结构的振动和控制特性。

4数值算例

算例1令半锥角α=0°，不考虑压电载荷的作用，式(20)可退化为一个被动约束层阻尼圆柱壳的动力学控制方程。考虑一个两边固支被动约束层阻尼圆柱壳，参数如下[5]：L=0.1 m，R10=0.1 m，h1=0.003 m，h2=0.002 m，h3=0.001 m，E1=E3=70 GPa，μ1=μ3=0.3，G2=0.896(1+0.968i) MPa，ρ1=ρ3=2 700 kg/m3，ρ2=1 340 kg/m3。本文方法计算的固有频率与文献[5]的比较列于表1。

表1　固有频率与文献值的比较

由表1中数据可以看出，本文的计算结果与文献值吻合得非常好。

图2　ACLD壳与PCLD壳位移响应比较Fig.2 Comparison of displacement response with ACLD shell and PCLD shell

由图2可以看出，在施加了压电力后，位移大幅减小，ACLD结构的减振效果优于PCLD结构。但是，随着频率的增高，两种阻尼结构的差别逐渐减小，在2 000 Hz附近几乎没有差别。这是由于压电材料所产生的压电力很小，在高频振动时已几乎不起作用，因此，ACLD结构中的主动控制仅适用于中低频段内的振动控制，在高频段内被动控制起主要作用。

为了考察反馈系数的影响，令反馈系数kd分别为1×105、1×106、1×107，计算出来的位移响应如图3所示。由图中可看出，反馈系数越高，减振效果越好。

算例3为考察反馈点位置的影响，令kd=1×106，其余参数与算例2相同，反馈点分别位于中点和自由端，计算两点的位移响应，分别如图4和图5所示。

由图4可以看出，当反馈点在自由端时，该点的位移较小。由图5可以看出，当反馈点在中点时，中点的位移小于自由端的位移。

为了进一步讨论反馈点的位置对振动特性的影响，当频率f=800 Hz时，令反馈点与固定端的距离d分别为0.2 m、0.4 m、0.6 m时，基壳中面母线的无量纲位移曲线如图6所示。由此可见，ACLD结构在它的反馈点可获得最好的抑制效果。

图3　不同反馈系数时位移响应比较Fig.3 Comparison of displacement response with various feedback coefficients

图4　不同反馈点自由端位移响应Fig.4 Displacement responses of the free end with various feedback point

图5　不同反馈点中点位移响应Fig.5 Displacement responses of the mid-point with various feedback point

图6　不同反馈点时母线的位移图Fig.6 Displacement responses of the meridian with various feedback point

5结论

考虑压电约束层的正、逆压电效应，导出了作用于压电约束层的主动控制力，将它引入圆锥壳的平衡方程和内力—位移关系，在原有PCLD圆锥壳的基础上，导出了ACLD圆锥壳的机电耦合控制方程，并基于叠加原理提出了一种求解此类方程的半解析方法，分析了结构的振动和控制特性。研究表明，ACLD在中低频段具有良好的减振效果；速度反馈系数越大，振动的抑制效果越好；反馈点的选择对结构的阻尼特性有较大的影响，反馈点应尽量位于变形较剧烈的位置或最需要控制的位置。利用本文所建立的模型，对ACLD圆锥壳的结构参数进行优化，可望获得理想的控制和阻尼特性。由于采用解析模型和齐次扩容精细积分法，本文方法的计算量小，高频段内稳定性强，且参数改变时不需要重新建模，非常适合于ACLD结构的优化设计。

参 考 文 献

[1] Biswas D,Ray M. Active constrained layer damping of geometrically nonlinear vibration of rotating composite beams using 1-3 piezoelectric composite[J]. International Journal of Mechanics and Materials in Design,2013,9:83-104.

[2] Vasques C MA,Mace B R,Gardonio P,et al. Arbitrary active constrained layer damping treatments on beams:Finite element modeling and experimental validation[J]. Computer and Structure,2006,84:384-1401.

[3] Ray M C,Shivakumar J. Active constrained layer damping of geometrically nonlinear transient vibrations of composite plates using piezoelectric fiber-reinforced composite[J]. Thin-walled Structures, 2009,47:178-189.

[4] Ray M C,Reddy J N. Active control of laminated cylindrical shells using piezoelectric fiber reinforced composites[J]. Composites Science and Technology,2005,65:1226-1236.

[5] 李恩奇,李道奎,唐国金,等. 约束层阻尼圆柱壳动力学分析[J]. 工程力学,2008,25(5):6-11.

LI En-qi,LI Dao-kui,TANG Guo-jin,et al. Dynamic analysis of constrained layer damping cylindrical shell[J]. Engineering Mechanic,2008,25(5):6-11.

[6] 李恩奇,唐国金,雷勇军,等. 约束层阻尼板动力学问题的传递函数解[J]. 国防科技大学学报,2008,30(1):5-9.

LI En-qi,TANG Guo-jin,LEI Yong-jun,et al. Dynamic analysis of constrained layer damping plate by the transfer function method[J]. Journal of National University of Defense Technology,2008,30(1):5-9.

[7] Yuan L Y,Xiang Y,Huang Y Y,et al. A semi-analytical method and the circumferential dominant modal control of circular cylindrical shells with active constrained layer damping treatment[J]. Smart Materials and Structures,2010,19(2),025010(14pp).

[8] Kumar A,Ray M C. Control of smart rotating laminated composite truncated conical shell using ACLD treatment[J]. International Journal of Mechanical Sciences,2014,89:123-141.

[9] 陆静,向宇,倪樵,等. 分析部分环状覆盖PCLD圆锥壳自由振动与阻尼特性的半解析法[J]. 振动工程学报,2010,23(2):213-219.

LU Jing,XIANG Yu,NI Qiao,et al. A semi-analytical method for analyzing free vibration and damping effect of a conical shell with partially ring-shaped constrained layer damping treatment[J]. Journal of Vibration Engineering,2010,23(2):213-219.

[10] Hu Y C,Huang S C. The frequency response and damping effect of three-layer thin shell with viscoelastic core[J]. Journal of Computers and Structures,2000,76:577-591.

Control characteristics of a conical shell covered with active constrained layer damping

LU Jing, YUAN Li-yun

(College of Automobile and Transportation, Guangxi University of Science and Technology, Liuzhou 545006, China)

Abstract:Based on the constitutive relation and internal force-displacement equation of piezoelectric materials, dynamic and electrical control equations of piezoelectric constrained layer were derived considering positive and inverse piezoelectric effects. According the geometric properties of a conical shell covered with active constrained layer damping, the variables were expanded along circumferential direction with Fourier series, and the equations mentioned above were converted as a first-order differential matrix equation along meridian direction. Combining normal equilibrium equations and displacement continuity conditions of visco-elastic layer, the dynamic equations of the laminated structure were derived with dynamic equations of the active constrained layer and the base shell. Combining these equations and the electrical control equations of the piezoelectric constrained layer, the electromechanical coupling model of the conical shell covered with active constrained layer damping was built. Then, applying the speed feedback control strategy, a semi-analytical and semi-numerical method was proposed with the precise integration technique and the superposition principle. Finally, the effects of parameters, such as, feedback coefficient, positions of feedback points on vibration and control characteristics of the conical shell covered with active constrained layer damping were analyzed with the proposed method.

Key words:active constrained layer damping; conical shell; speed feedback control strategy; electromechanical coupling; control characteristics

基金项目：国家自然科学基金(51105083;11162001)； 广西自然科学基金(2012GXNSFAA053207)

收稿日期：2014-12-24修改稿收到日期：2015-05-20

中图分类号:TH133；TU311

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.022

第一作者 陆静 女，博士，教授，1973年6月生