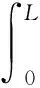通过PVDF阵列设计阶梯梁的模态传感器

钟海彬， 毛崎波

(南昌航空大学 飞行器工程学院，南昌　330063)

通过PVDF阵列设计阶梯梁的模态传感器

钟海彬， 毛崎波

(南昌航空大学 飞行器工程学院，南昌330063)

摘要：以两端固支阶梯梁为例，通过高分子压电薄膜(Poly Vinyli Dene Fluoride，PVDF)传感器阵列测量其模态坐标。在该阶梯梁表面均匀黏贴一组相同形状的矩形PVDF薄膜，首先通过实验方法直接测得该阶梯梁的曲率模态，然后把曲率模态作为这组PVDF输出信号的加权因数，从而得到所需的模态坐标。实验结果表明，这种传感器设计方法是可行的，并且PVDF阵列式模态传感器具有在不均匀梁结构表面布置方便，能准确、方便的测出实验曲率模态，不受激励力位置影响，滤波效果好等优点。

关键词：PVDF传感器；实验模态分析；曲率模态；模态滤波；阶梯梁

近几年来，通过设计压电式模态传感器实现结构振动和噪声主动控制的研究越来越引起关注[1-5]。通过设计不同的压电模态传感器，可以测量振动结构表面的体积位移、声辐射模态、体积速度等物理量，此前一些学者对此作了大量研究[6-12]。一般来说，有两种模态传感器的设计方法，一种是设计特定形状的连续分布式模态传感器[2,6-7,12-14]，这种形式的模态传感器对边界条件存在一定的依赖，当边界条件改变时往往需要重新选择传感器的形状函数才能保证被测振动参数的准确性。同时对于某些结构，特定形状的连续分布式模态传感器的加工和布置也存在一定的难度；而且设计的传感器互换性较差，只能检测某一阶特定模态，这无疑对工程应用带来很多不便。如文献[14]中研究者利用特定形状的分布式PVDF传感器设计阶梯简支梁的模态传感器，为得到所需模态坐标必须设计相当复杂的的PVDF形状，同时也易受边界条件的制约。

另一种是设计离散阵列式模态传感器[15-16]，通过设计一组相同形状的矩形PVDF压电薄膜的加权系数来得到需要测量的振动参数。这种方法不用预先设计传感器的形状函数，简化了复杂的数值计算过程。同时，只需改变加权系数就能很方便的得到目标阶模态，而且不易受边界条件的影响。利用设计的模态传感器对振动结构进行模态滤波，精确识别振动参数，继而对结构振动和噪声进行主动控制。目前对阵列式模态传感器的研究主要集中在均匀结构(如均匀梁或均匀薄板)的理论研究，实验研究较少。并且在设计加权系数时一般需要进行复杂的数值计算(如Adomian方法[12]、微分变换法(DTM)[17]、伪逆方法[18]等)。

为了简化阵列式模态传感器的设计，并进一步推广其适用范围，本文以含有三个阶梯的两端固支梁为例，利用一组矩形PVDF阵列作为传感器，通过实验模态方法直接测量结构的曲率模态，并把实验测得的各阶离散曲率模态作为相应的PVDF压电传感器的加权系数，从而得到所需的模态坐标。

1基本理论

1.1阵列式PVDF模态传感器设计

设有一阶梯梁，考虑在振动梁上均匀布置n块同样形状的矩形PVDF薄膜，如图1所示。假设第kPVDF的输出信号为H(k)。为了实现阶梯梁的模态滤波，得到模态坐标，对第k块PVDF输出信号设计加权系W(k,m)，如图1所示，使得加权后的输出为阶梯梁第m阶模态坐标Am。

由图1可知，加权后的总输出信号为：

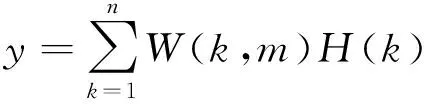
(1)

式中,W(k,m)表示第m阶模态下第k块PVDF传感器的加权系数。

假设有外界激励力作用在x=xf处，由文献[19-20]的研究可知，激励力与第k块PVDF输出之间的频率响应函数可表示为：

(2)

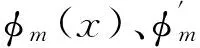
由模态分析理论可知，梁的第m阶模态坐标A(m)可表示为：

(3)

式中,F表示激励力的幅值。

联立(2)、(3)再代入(1)，总输出信号可重新表示为：

(4)

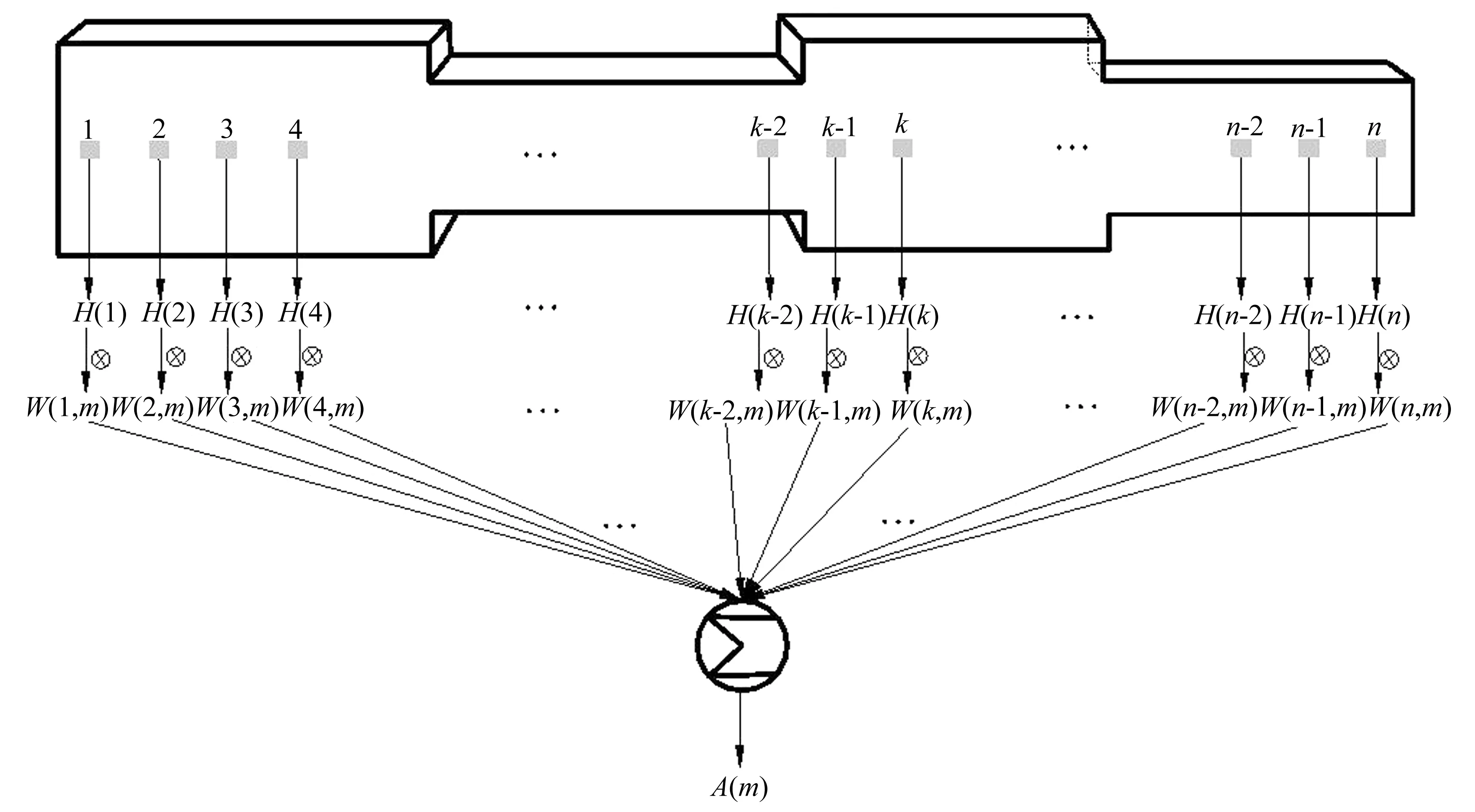
图1　阵列式压电模态传感器原理Fig.1 Theory of the piezoelectric modal sensor array

由拉格朗日微分中值定理，式(4)可表示为：

(5)

其中xξ满足xk-l/2

对于经典边界条件(简支、固支、自由端)，结构曲率模态具有正交性：

(6)

式中，下标u,v表示第u,v阶曲率模态。

式(6)保证了实验测得的各阶模态是相互独立的。由文献[20]的研究，对结构曲率模态进行离散处理，得到的离散曲率模态也是正交的，即:

(7)

式中,c为非零常数。

由式(7)知，如果在式(5)中把第m阶离散曲率模态值作为PVDF的加权系数，即：

W(k,m)=φ″m(xξ)

(8)

把式(8)代入式(5)，则加权后的PVDF阵列输出为：

(9)

从式(9)可以发现，当用第m阶离散曲率模态值作为加权系数来对阶梯梁进行模态滤波得到的是第m阶模态坐标。

1.2阵列式PVDF实现实验曲率模态测量

由阵列式PVDF模态传感器的设计可以看出，只要能知道相应的实验离散曲率模态的值，就可以得到阵列式PVDF的加权系数向量，进而可以在实验条件下直接测得阶梯梁的相应模态坐标Am。

注意到目前对曲率模态的研究一般是通过结构模态而展开[21-23]。也就是说，首先通过传统的加速度计进行实验模态分析得到其结构模态，然后通过对结构模态进行中心二次差分、多项式插值等数值方法得到其曲率模态。但是对结构模态进行二阶导数有可能放大其测量误差，使得数值处理得到的曲率模态往往失真。近来Wang等[19-20]理论上证明了通过压电材料直接测量结构曲率模态的可行性。本文在文献[19-20]的基础上进一步从实验角度验证通过PVDF阵列直接测量结构的曲率模态。

对式(2)运用拉格朗日微分中值定理，式(2)可重新表示为：

(10)

式中xξ满足xk-l/2

从式(10)可以发现，当激励点位置xf固定(即为φm(xf)为常数)，PVDF传感器按梁的n等分点均匀移动，可以测量到阶梯梁的曲率模态φ″m(xξ)的n个离散值。通过实验模态分析软件即可得到离散曲率模态的值。

2实验研究

为了验证本文的阵列式PVDF模态传感器的滤波效果，取一铝质阶梯梁进行实验研究。如图2所示，阶梯梁有效长度为800 mm，阶梯位置位于200 mm、440 mm、640 mm处，每段阶梯对应的宽度分别为50 mm、40 mm、50 mm、30 mm，厚度均为5 mm。阶梯梁被平均分成20个单元，20片PVDF传感器贴于阶梯梁的背面，位于每个单元的中央区域。PVDF的物理参数见表1。

表1　PVDF传感器物理参数

实验过程中，用LC-01A冲击力锤作为外部力源位于xd处，通过力锤上的CL-YD303力传感器测量激励力，把布置在1～20号单元上的PVDF传感器输出信号传入江苏联能YE6251数据采集仪，采样频率设置为4 kHz,采用上升沿触发。实验整体过程如图2所示，首先力锤位于A点：xd=80 mm处，测量PVDF薄膜的输出信号H(k)。将测得的输出信号导入南京航空航天大学研发的N-Modal模态分析软件进行数据分析，得到实验离散曲率模态，然后直接把该离散曲率模态数值作为阵列式PVDF加权系数，用每片PVDF的输出信号乘以相应的加权系数后相加得到各阶模态坐标。

表2是实验阶梯梁前五阶固有频率实验值, 为避免电噪声对实验设备的影响，取2～5阶模态进行分析。图3表示A激励点xd=80 mm时，PVDF频率响应曲线, 由图可以看出，每片PVDF的输出信号测得的各阶模态下的频率是一致的。

图2　阶梯梁实验示意图 Fig.2 Diagram of the stepped beam experiment

图4表示实验曲率模态分析的2～5阶模态置信矩阵(Modal Assurance Criterion，MAC)直方图，由图可以看出对角线元素的值均为100，其他元素值远小于对角元素，说明各阶曲率模态具有很好的独立性，模态分析效果很好。

表2　实验梁前5阶固有频率实验值

图3　A激励点下PVDF频率响应曲线Fig.3 Frequency response function of PVDF films under A incentive point

图4　曲率模态置信矩阵直方图Fig.4 MAC of the experimental beam (curvature mode shapes)

由式(10)和式(8)可知，实验模态分析得到的结构曲率模态离散值即为PVDF阵列的加权系数。图5表示A激励点下实验测得的PVDF加权系数直方图。

图6表示通过PVDF阵列得到的实验输出信号平均值，由于只分析2～5阶模态，频率截断到1 500 Hz。图7是利用图5中相应的加权系数对实验阶梯梁进行模态滤波得到的结果。从图7中2到5阶模态滤波可以看出，各目标阶固有频率处峰值明显高于非目标阶固有频率处峰值，说明模态传感器对目标阶模态的滤波效果很好。对比图6和图7可看出，非目标阶固有频率处的峰值也明显下降，但仍未能全部滤除，这与梁表面划分的单元数目和PVDF传感器数量有关，由于传感器数量有限使得只有部分模态参与滤波，使得非目标阶模态仍出现小的峰值。

图5　PVDF加权系数直方图Fig.5 Weighting coefficient histogram of PVDF films

图6　PVDF传感器阵列输出信号平均值Fig.6 Average outputs of PVDF films

图7　A激励点下实验梁滤波效果Fig.7 Modal filtering results of the experimental beam under A incentive point

由于PVDF阵列的加权系数与外激励力性质(如激励力类型、频率以及位置等)无关[24]，所以通过该加权系数可以测量任意激励下的模态坐标。图8表示当激励力移动到B点：xd=260 mm时，通过图5所示的PVDF加权系数得到的模态坐标。由图8可以看出，当激励点改变后，频率响应曲线的幅值发生了相应的变化。非目标阶模态幅值与目标阶模态幅值相比，有明显下降。对比图7和图8可以看出，设计出来的PVDF阵列式模态传感器对激励点A、B具有同样明显的滤波效果，对模态坐标的识别效果很好。这也说明了模态传感器不受激励力位置影响。

图8　B激励点下实验梁滤波效果Fig.8 Modal filtering results of the experimental beam under B incentive point

文献[25]讨论了矩形PVDF薄膜大小对测量的影响，当矩形PVDF传感器过大时，其输出电荷会受到结构轴向振动的影响，从而对模态滤波产生影响。该文献的实验结果表明，当采用30 mm×12 mm的矩形PVDF时，可以精确测量1 400 Hz内的结构法向振动信息。因此本文采用了文献[25]建议的30 mm×12 mm的矩形PVDF，避免了轴向振动对模态分析的影响。

为了更好地说明PVDF传感器数目对模态分析精度的影响，在A激励点下，取图5中序号为偶数的PVDF传感器进行滤波分析。图9为10片PVDF的加权系数，图10为相应的滤波效果。对比图7和图10可以发现，采用10片PVDF的滤波效果与20片PVDF时基本相同。这主要是因为1 500 Hz内只包含8阶结构模态。文献[5,15-17,25-26]已经证明：M片PVDF可以实现在频率范围0～ωM内的模态滤波。文献[26]分析了PVDF布置间距失谐的情况，从中可以看出，对PVDF的布置进行一定优化，可以减少对非目标阶模态的滤除误差。对于本文中前8阶模态滤波效果，主要受PVDF传感器数目的影响，当取10片或20片PVDF时，滤波效果已经满足模态识别要求。

图9　10片PVDF加权系数直方图Fig.9 Weighting coefficient histogram of ten PVDF films

图10　10片PVDF实验梁滤波效果Fig.10 Modal filtering results of the experimental beam with ten PVDF films

3结论

本文通过实验方法设计阶梯梁的PVDF阵列式模态传感器，把模态传感器推广应用于非均匀结构。这种方法的优点在于：只需要测量一组在某一激励力下PVDF阵列的频率响应函数，就可以通过实验模态分析方法得到PVDF阵列的加权系数，该PVDF加权系数可用于计算任意激励下的模态坐标。同时本文方法一个重要优点是不需要任何复杂的数值计算。实验结果表明本文方法的模态滤波效果良好，基于阶梯梁结构模态测试结果，该理论框架可以拓展至一般复杂结构。

参 考 文 献

[1] 毛崎波，姜哲. 通过压电式传感器进行简支梁声辐射有源控制[J].声学学报，2001,26(6):527-531.

MAO Qi-bo，JIANG Zhe. Active control of sound Radiation from simply supported beam using piezoelectric sensors[J]. Journal of Acoustics,2001,26(6):527-531.

[2] 靳国永，刘志刚，杜敬涛,等. 基于分布式体积速度传感的结构声辐射有源控制实验研究[J]. 声学学报，2009,34(4):342-349.

JIN Guo-yong,LIU Zhi-gang,DU Jing-tao. Experimental study on active structural acoustic control based on distributed structural volume Velocity sensors[J]. Journal of Acoustics,2009,34(4):342-349.

[3] 马玺越，陈克安，玉昊昕,等.PVDF阵列构建结构声辐射有源控制误差传感策略[J]. 振动工程学报，2013,26(5):797-806.

MA Xi-yue,CHEN Ke-an,YU Hao-xi,et al. Error sensing strategy for active control of panel radiated sound using PVDF arrays[J]. Journal of Vibration Engineering,2013,26(5):797-806.

[4] 马玺越，陈克安，丁少虎,等.基于平面声源的三层有源隔声结构误差传感策略研究[J]. 机械工程学报，2013,49(11):70-78.

MA Xi-yue,CHEN Ke-an,DING Shao-hu,et al. Error sensing strategy for active triple-panel sound insulation structure using planar source[J].Journal of Mechanical Engineering,2013,49(11)：70-78.

[5] Pietrzko S J,Mao Q. New results in active and passive control of sound transmission through double wall structures[J]. Aerospace Science and Technology,2008,12(1):42-53 .

[6] 毛崎波，徐柏龄. 利用压电高分子薄膜设计声辐射模态传感器[J]. 声学学报，2003，28(3):262-266．

MAO Qi-bo,XU Bo-ling.Design radiation mode sensor using PVDFfilm[J]. Journal of Acoustics,2003,28(3):262-266.

[7] 杜敬涛，靳国永，杨铁军,等.基于分布式压电传感器的结构表面体积速度测量实验研究[J]. 振动工程学报,2008,21(3):235-240.

DU Jing-tao,JIN Guo-yong,YANG Tie-jun,et al.Experimental study on measurement of structural surface volume velocity based on distributed Piezoelectric sensor[J]. Journal of Vibration Engineering, 2008,21(3):235-240.

[8] Mao Q,Pietrzko S．Research on volume displacement sensor[C]//ICAST 2008-International Conference on Adaptive Structures and Technologies, Ascona,Switzerland, 2008 ．

[9] 李双，陈克安. PVDF声辐射模态传感器设计中的关键问题研究[J]. 西北工业大学学报， 2007，25(2)：295-300.

LI Shuang,CHEN Ke-an.On Improving the method for designing acoustic radiation mode sensor using PVDF films[J]. Joumal of Northwestern Polytechnical University,2007,25(2):295-300.

[10] Mao Q，Pietrzko S. Measurements of local volume displacement using a piezoelectric array[J]. Acta Acustica United with Acustica,2006,92(4):556-566．

[11] Mao Q. A piezoelectric array for sensing radiation modes[J]. Applied A-coustics,2003,64:669-680．

[12] Mao Q，Pietrzko S. Design of shaped piezoelectric modal sensor for a type of non-uniform beams using adomain-modofied decomposi-tion method[J]. Journal of Intelligent Material Systems and Structures,2011，22:149-159．

[13] Jian K,Ffiswell M.I. Designing distributed modal sensor for plate structure using finite element analysis[J]. Mechanical Systerms and Signal Processing,2006,20:2290-2304.

[14] Anthony D K.Modal detection for non-uniform thickness beams using continuous strain sensors and a strain-energy-based orthogonality condition[J]. Journal of Sound and Vibration,2008(1/2):65-87.

[15] Preumont A,Francois A,De Man P. Spatial filters in structural control[J]. Journal of Sound and Vibration,2003,265:61-79.

[16] Sumali H,Meissner K,Cudey H H. A piezoelectric array for sensing vibration modal coordinates[J]. Sensors and Actuators A,2001，93：123-131.

[17] Mao Q. Design of piezoelectric modal sensor for non-uniform Euler-Bernoulli beams with rectangular cross-section by using differential transformation method[J]. Mechanical Systems and Signal Processing,2012,33:142-154.

[18] 朱峤，毛崎波.阵列式压电模态传感器的实验研究[J]. 传感器与微系统，2014，33(2):61-64.

ZHU Qiao,MAO Qi-bo.Experimental research on piezoelectric array modal sensors[J].Transducer and Microsystem Technologies,2014,33(2):61-64.

[19] Wang B T. Structural modal testing with various actuators and sensors[J]. Mechanical Systems and Signal Processing,1998,12(5):627-639.

[20] Wang B T. Vibraion analysis of continuous system subject to generic forms of actuation forces and sensing devices[J]. Journal of Sound and Vibration,2009,319:1222-1251.

[21] Chen R L,Wang B T. The use of polyvinylidene fluoride films as sensors for the experimental modal analysis of structures[J]. Smart Materials and Structures,2004,13:791-799.

[22] 何钦象，杨智春，姜峰,等. 薄板损伤检测的高斯曲率模态差方法[J].振动与冲击，2010,29(7)：112-115.

HE Qin-xiang,YANG Zhi-chun,JIANG Feng,et al. Damage detection for an elastic thin plate based on Gauss curvature modal difference[J]. Journal of Vibration and Shock,2010,29(7):112-115.

[23] 刘义伦,时圣鹏,廖伟. 利用曲率模态识别桥梁损伤的研究[J]. 振动与冲击,2011,30(8):77-81.

LIU Yi-lun,SHI Sheng-peng,LIAO Wei.The research on bridge damage identification using curvature mode shapes[J]. Journal of Vibration and Shock,2011,30(8):77-81.

[24] Fan Wei, Qiao Pi-zhong. Vibration-based damage identification methods:a review and comparative study[J]. Structural Health Monitoring,2011,10(1):83-111.

[25] Mao Qi-bo,Pietrzko S J. Measurements of local volume displacement using a piezoelectric array[J]. Acta Acustica United with Acustica,2006,92:556-566.

[26] Pagani C C,Trindade M A. Optimization of modal filters based on arrays of piezoelectric sensors[J]. Smart Mater.Struct,2009,18:1-12.

Design of modal sensors for a stepped beam based on PVDF array

ZHONG Hai-bin, MAO Qi-bo

(School of Aircraft Engineering, Nanchang Hangkong University, Nanchang 330063,China)

Abstract:With an example of a clamped-clamped beam containing multiple steps, a new test approach was presented to design modal sensors by using an array of polyvinylidene fluoride (PVDF) sensors. An array of rectangular segments of PVDF film uniformly was stuck on the surface of the beam, was taken as sensors. Firstly, an experimental modal analysis method was applied to obtain the beam’s curvature modal shapes directly. Then the measured curvature modal shapes were taken as the corresponding weighted coefficients of the output signals of the PVDF films, the weighted combinations of the outputs directly lead to the target modal coordinates. The experimental results showed that PVDF array modal sensors have advantages of easily bonded on the surface of the stepped beam,accurately and conveniently measuring tested curvature modes, independence of positions of external excitations, and good effect of modal filtering, etc.

Key words:PVDF sensors; experimental modal analysis; curvature mode; modal filtering; stepped beam

基金项目：国家自然科学基金资助项目(51265037;11464031)；江西省高等学校科技落地项目(KJLD12075)

收稿日期：2015-03-09修改稿收到日期：2015-05-15

通信作者毛崎波 男，博士,教授，1975年生

中图分类号:TP212.9

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.020

第一作者 钟海彬 男，硕士，1990年生