湿式离合器接合过程摩擦振颤机理研究

杨立昆， 李和言， 马　彪

(北京理工大学 车辆传动国家级重点实验室，北京　100081)

湿式离合器接合过程摩擦振颤机理研究

杨立昆， 李和言， 马彪

(北京理工大学 车辆传动国家级重点实验室，北京100081)

摘要：通过建立4自由度动力学模型，研究了湿式离合器在接合过程中的摩擦振颤问题。基于稳态的非线性LuGre摩擦模型，通过特征值方法进行稳定性分析，并基于MATLAB/Simulink对该动力学模型进行数值仿真。结果表明，摩擦因数随相对滑动速度的负梯度变化及接触界面的压力波动是摩擦振颤发生的主要原因，在不稳定状态下，静、动摩擦因数之差越大，压力波动频率越接近不稳定模态固有频率，振颤越强烈；同时阻力矩激励也会对摩擦振颤产生与压力波动相同的效果。

关键词：离合器振颤;摩擦因数负梯度变化;接触压力波动;阻力矩激励

湿式离合器作为车辆传动系统的重要部件，在各类型的变速器上都有较多的应用。作为一种典型摩擦元件，湿式离合器在接合过程中可能伴随着不稳定的振颤现象。摩擦振颤是一种发生在两相对滑摩表面的非线性振动，与接触界面的摩擦特性、系统动力学特征和外部载荷等因素有关。摩擦振颤的发生会严重影响离合器的接合品质，加速摩擦表面的磨损，降低传动系统寿命。所以有必要对湿式离合器的摩擦振颤进行研究，为抑制其发生及为离合器的优化提供依据。

国外对于离合器摩擦振颤问题的研究相对较多，主要以制动器的摩擦啸叫理论为基础。Crowther等[1-2]从μ-vrel变化特性的角度分析了自动变速器用离合器的振颤问题，基于特征值分析认为振颤主要归因于摩擦因数随离合器主从动部分相对速度的负梯度变化。Centea等[3-4]通过建立含多约束的传动系统扭振模型，研究了某一机械干式离合器的振颤现象，并分析了不同参数对离合器振颤的影响。Duan等[5-7]认为摩擦因数的负梯度变化非唯一因素，通过建立2自由度扭振模型，他们还考虑了简谐变化的法向力对闭锁离合器摩擦自激振动的影响。国内在这方面研究相对较少，主要从摩擦因数线性负梯度变化的角度分析离合器的摩擦振颤[8-10]。

本文建立了4自由度动力传动系统动力学模型，基于摩擦因数负梯度变化理论和切向-法向模态耦合理论全面阐述湿式离合器摩擦振颤的发生机理，同时通过稳定性分析确定摩擦振颤发生的临界条件；通过数值计算和仿真，探讨不同参数对离合器摩擦振颤的影响。

1理论分析

摩擦力是摩擦引发的振动的激励源[11]，对于湿式离合器，其某一接触界面间的摩擦力可表达为

Ff=μ(vrel)p(t)A

(1)

式中：μ(vrel)为摩擦副的摩擦因数，是相对滑动速度的函数；p(t)为摩擦副间接触压力，为时间的函数；A为摩擦副名义接触面积，认为在接合过程中保持不变。可见，离合器接合过程的摩擦力同时受摩擦因数和接触压力的制约，而二者从不同机理上影响摩擦力变化，进而影响摩擦振颤特性。

以往的研究已经证实摩擦表面的黏滑运动，即摩擦因数随相对滑动速度的负斜率变化给系统导入负阻尼环节，从而在一定条件下引发摩擦自激振动。同时，由式(1)可以看出摩擦界面法向接触压力的变化会直接导致切向摩擦力的变化，通过这种法向模态与切向模态的耦合关系引发系统不稳定的振动。所以本文将综合黏滑运动与模态耦合理论，分析离合器的摩擦振颤机理。

2动力学模型

离合器的正常滑摩主要发生在车辆起步和换挡过程中。为便于分析，本文将动力传动系统简化为4自由度动力学模型，如图1所示。模型包括驱动装置等效惯量J1、离合器主动部分等效惯量J2、离合器从动部分等效惯量J3及负载端等效惯量J4。

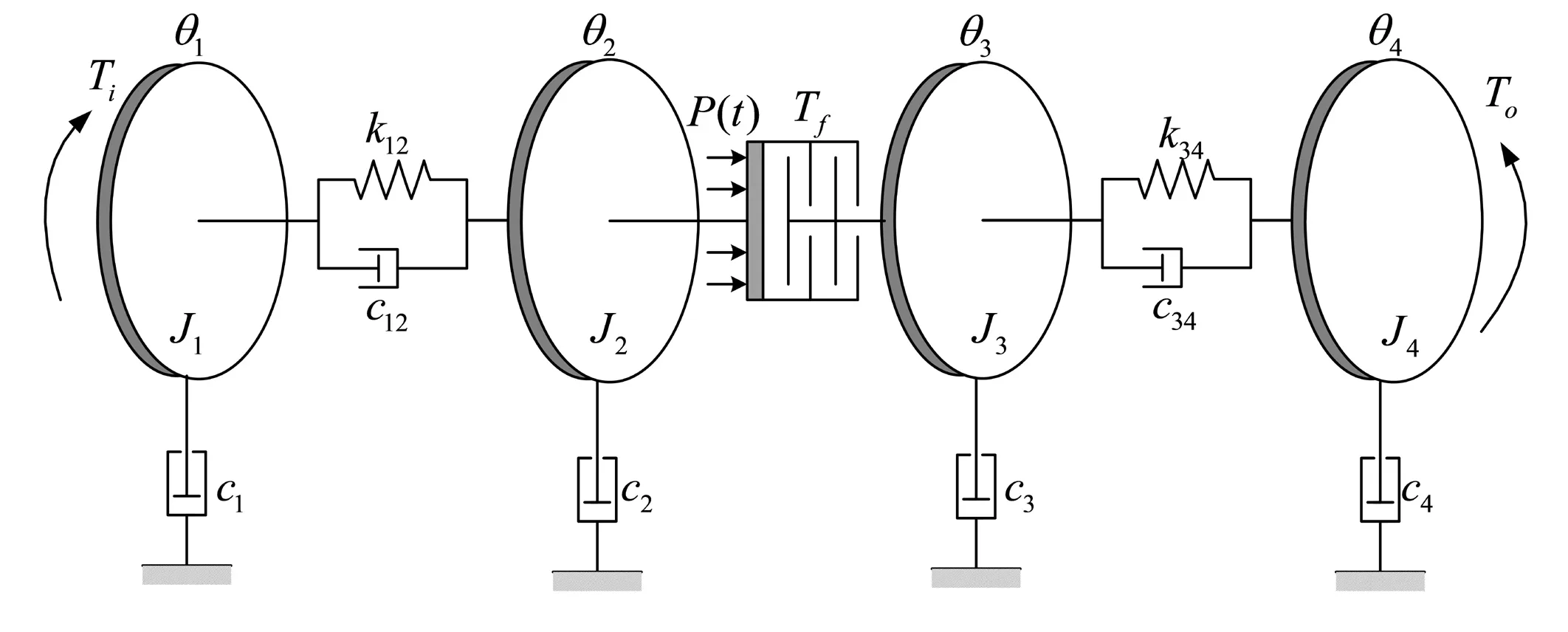
图1　4自由度动力传动系统动力学模型Fig.1 4DOF power-train dynamic model

在离合器滑摩过程中，系统动力学方程可表述为

(2)

(3)

(4)

(5)

式中：θ1、θ2、θ3、θ4分别为各惯量的绝对角位移；c1、c2、c3、c4为相应各部分的等效黏性阻尼系数；c12、c34和k12、k34分别为输入轴和输出轴的黏性阻尼和扭转刚度；Ti为驱动装置输出转矩；To为阻力矩；Tf为离合器摩擦力矩，其值为

(6)

(7)

式中：μk为库伦动摩擦因数；μs为静摩擦因数；δ为常数，主导摩擦因数关于相对滑动速度变化的斜率，是后续分析的关键参数之一。

同时，由于换挡阀等元件的特性、湿式离合器所处的润滑环境及离合器滑摩过程中的非均匀接触等因素，离合器摩擦副间接触压力也是不断变化的。根据试验测试结果，将其假定为正弦变化的形式，则接触压力为

p(t)=pm+ppsinωt

(8)

式中：pm为名义接触压力；pp为压力变化幅值；ω为压力变化角频率。

3稳定性分析

(9)

进一步将其进行标准化处理

(10)

式中：Δμ=μs-μk，为静、动摩擦因数差。则根据式(6)可得离合器的摩擦转矩

(11)

进一步可将动力学方程式(2)～(5)等效为矩阵的形式，即

(12)

其中：

因而系统的雅克比矩阵为

(13)

根据Lyapunov稳定性理论，雅克比矩阵J的特征值可作为稳定性判定的依据。若该8阶矩阵所有特征值的实部均不大于零，则系统稳定或临界稳定；若存在一个实部大于零的特征值，则系统不稳定，且该特征值对应的虚部为不稳定模态的角频率[13]。系统参数如表1所示，稳定性分析暂不考虑压力波动的影响。

根据试验获得的某一湿式离合器摩擦特性，静摩擦因数μs为0.2。通过计算不同δ值及不同Δμ/μs下的雅克比矩阵特征值，并从8个特征值中选择最大实部，所得变化关系如图2所示。可见，当δ≤0时，最大特征值实部均不大于0；而当δ>0时，存在实部大于0的特征值，且最大实部随δ的增大而增大，表明当摩擦因数负梯度变化时，系统阻尼矩阵C被引入负阻尼，系统失去稳定性；且负梯度程度越大，引入的负阻尼越大，系统稳定性越差。同时，特征值最大实部随Δμ/μs的增加而明显增大，所以当摩擦因数负梯度变化时，静、动摩擦因数相差越大，系统稳定性越差。

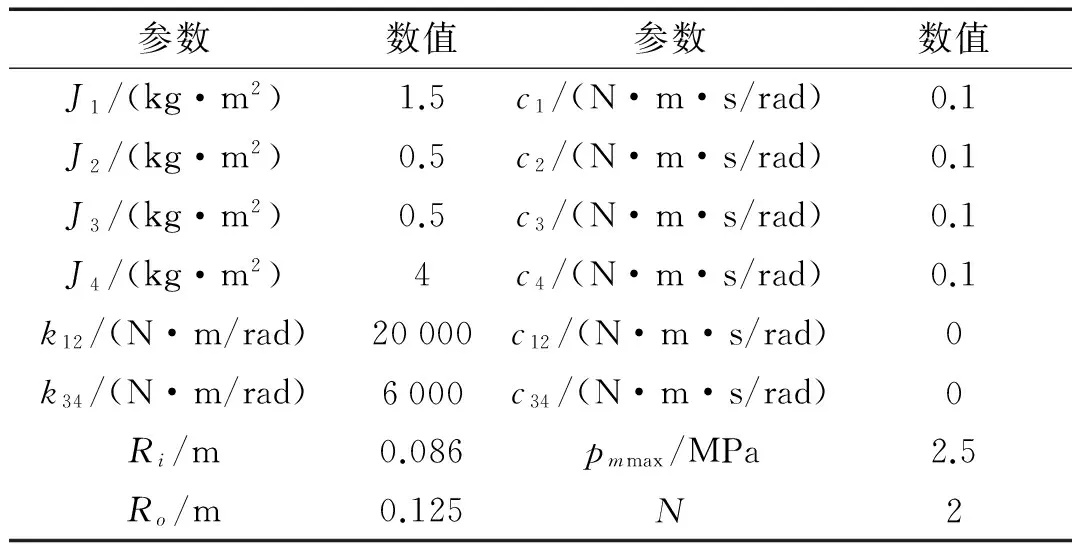
表1　动力学模型的相应参数

图2　不同条件下特征值最大实部变化Fig.2 Variation ofthe maximum real parts of the eigenvalues under different conditions

4计算与仿真

为验证所述理论分析的正确性，在MATLAB/Simulink环境中对动力学模型进行仿真分析。初始条件如下：

(1) 动力由某驱动装置提供，转矩与转速满足特定关系；

(2) 离合器主动部分初始转速为200 rad/s，从动部分转速为20 rad/s；

(3) 阻力矩名义值为500 Nm；

(4) 名义接触压力的变化过程如图3所示，在t=0.5 s时达到最大值2.5 MPa；

(5) 摩擦因数的变化如图4。

图3　名义接触压力的变化历程Fig.3 Variation profile of the mean contact pressure

图4　摩擦因数随相对滑动速度的变化Fig. 4 Variation of coefficient of friction with relative velocity

4.1摩擦因数与湿式离合器振颤

图5所示为摩擦因数为定值及随相对滑动速度线性变化与非线性变化三种情况下的离合器主从动部分转速变化情况。可见当摩擦因数为定值(COF1)时，主从动部分均没有出现转速的波动，离合器没有摩擦振颤发生。同时，在相同的δ及相同的Δμ/μs的情况下，当摩擦因数线性负梯度变化(COF2)时，离合器已显示出明显的振颤，这与第3节稳定性分析的结果一致；但当摩擦因数非线性负梯度变化(COF3)时，离合器并未出现明显的振颤行为，从动部分转速只有微小的波动。这主要因为摩擦因数非线性变化时的负梯度程度不及线性变化时，如图4所示，所以只有当负梯度达到某一程度时，单纯由摩擦因数负梯度变化引发的摩擦振颤才会比较强烈。

图5　不同摩擦因数下的离合器振颤Fig.5 Clutch judder with different coefficients of friction

如第2节所述，通过对湿式离合器的测试表明，其摩擦因数大都以公式(7)所示的非线性形式变化。针对非线性变化的情况，对于不同的δ值与Δμ/μs，离合器接合角速度曲线如图6所示。比较COF4与COF5可以发现，在非线性摩擦模型中，δ的变化对离合器摩擦振颤的影响并不明显，但可以改变离合器的接合时间。物理解释为：在非线性的情况下，δ的变化对摩擦因数负梯度程度的影响较小，但却会很大程度地改变摩擦因数的动态值(如图4)。随δ值的增大，动态摩擦因数值减小，致使摩擦转矩减小，从而接合时间延长。此外通过分析式(7)可知当δ较小时，摩擦因数的变化范围很小；δ较大时，摩擦因数从动摩擦因数到静摩擦因数呈阶跃变化，实际的负梯度变化过程并不存在，这两方面均会弱化振颤的发生。对比COF4与COF6可知Δμ/μs的变化对摩擦振颤有较大影响，且当Δμ/μs较大时，离合器摩擦振颤加强。所以控制离合器摩擦振颤的发生主要应该减小静摩擦因数与库伦动摩擦因数之差。

图6　不同δ与Δμ/μs时的离合器接合角速度曲线Fig.6 Clutch angular velocity curves with various δ and Δμ/μs

4.2接触压力与湿式离合器振颤

基于前述分析，摩擦副接触压力通过模态耦合的机理影响离合器振颤。在COF1和3中，离合器均没有明显的振颤发生。通过对系统动力学方程进行特征值分析，发现系统存在两个固有频率，分别为115.69 rad/s和230.44 rad/s。研究表明，由于离合器滑摩过程存在不均匀接触等因素，接触压力的波动可以达到较高的频率。在后续的分析中取一阶固有频率，近似均为115 rad/s。取接触压力变化幅值pp为名义压力的4%，即0.1 MPa，压力波动角频率ω=115 rad/s，通过仿真得不同摩擦因数下的离合器主从动部分角速度曲线如图7所示。可见，当接触压力发生微小波动，且波动频率等于系统固有频率时，离合器的振颤会显著增强。同时可以发现，摩擦因数负梯度变化时的角速度波动幅值略大于摩擦因数为定值的情况，所以两种机理共同作用下的振颤更强烈。

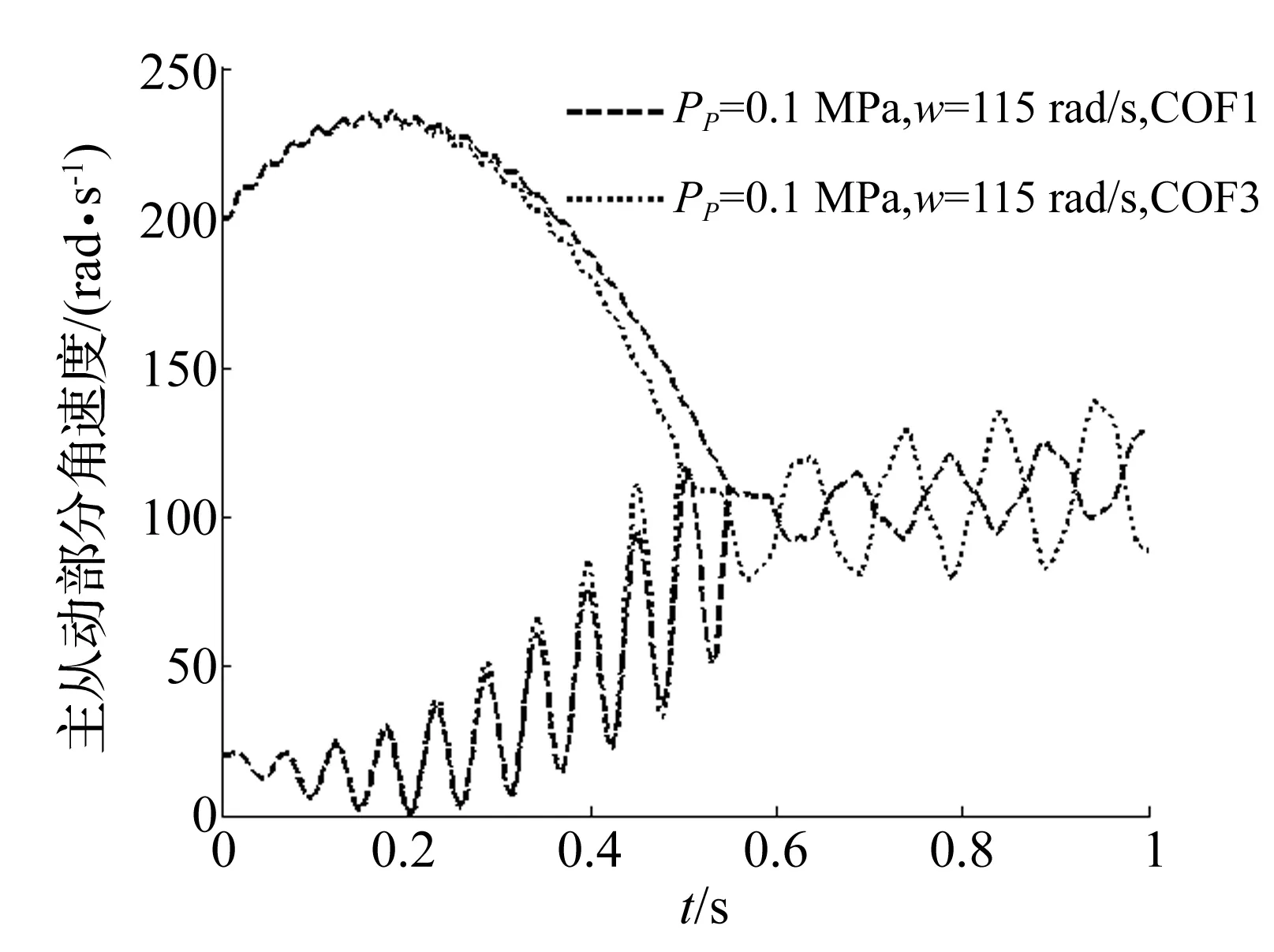
图7　接触压力波动对摩擦振颤的作用Fig.7 Effect of contact pressure fluctuation on clutch judder

分析COF3 ，将压力波动幅值增大至名义值的20%，即0.5 MPa，针对波动频率ω为65 rad/s、115 rad/s和165 rad/s三种情况，仿真结果如图8所示。进一步，图9所示为接触压力波动角频率与离合器摩擦振颤最大峰峰值之间的关系，其横坐标对应频率范围为0.8～32.6 Hz。从两图可以发现，波动频率远离固有频率时，压力幅值的增加并未明显增强振颤的发生；但当波动频率接近或等于固有频率时，振颤显著增强，离合器的动态特性已经明显失真。所以在离合器的设计和使用过程中，需要尽量避免控制压力波动频率接近系统固有频率，并力求抑制摩擦副接触界面压力波动的发生。

图8　不同压力波动频率下的接合角速度曲线Fig.8 Clutch angular velocity curves with different frequencies of contact pressure

图9　接触压力波动频率与离合器振颤的关系Fig.9 Relationship between pressure fluctuation frequency and clutch judder

4.3阻力矩激励的影响

外部阻力矩的不均匀变化可通过后传动系统传递到变速器输出轴上，进而在车辆纵向产生作用。为简化分析，将外部阻力矩激励简化为正弦变化的形式，即

To=Tom+Topsin(ωot+ψo)

(14)

式中：Top为阻力矩波动幅值；ωo为阻力矩波动角频率；ψo为ωo与ω之间相位差。假设阻力矩波动幅值为150 Nm，由于该分析不考虑接触压力波动，暂不考虑ψo的影响，分析结果如图10所示。对比三条曲线可以发现仅当ωo接近或等于不稳定模态固有频率时，阻力矩激励才会对离合器振颤产生较大影响，同时摩擦因数负梯度变化对应的振颤幅值高于摩擦因数为定值时的振颤幅值。

图10　不同阻力矩激励下的离合器接合角速度曲线Fig.10 Clutch angular velocity curves with different drag load excitations

考虑接触压力波动的情况，依然取pp=0.1 MPa，ω=115 rad/s，此时接触压力波动主导离合器摩擦振颤的发生。对激励频率ωo分别为65 rad/s和115 rad/s，相位差ψo=π,3π,…(反相位)和0,2π,…(同相位)的情况进行分析，结果如图11所示。可以看出，当ωo=65 rad/s时，外部激励对离合器振颤没有明显的影响；但是当ωo=115 rad/s时，外部激励对离合器的振颤产生影响，且激励频率与接触压力波动频率同相位时会增强振颤，而二者相位相反时，外部激励对振颤有一定的抑制作用。

图11　不同相位差下的接合角速度曲线Fig.11 Clutch angular velocity curves with different phase lags

5结论

(1) 离合器的摩擦振颤发生在一定的条件下，而摩擦因数随相对滑动速度的负梯度变化以及摩擦界面接触压力的波动是其发生的主要机理；

(2) 当摩擦因数非线性变化时，静、动摩擦因数差对振颤强度的影响较大，二者之差越小，振颤的强度越低；

(3) 摩擦界面的接触压力从波动幅值和波动频率两个方面影响离合器摩擦振颤的发生，波动幅值越大，波动频率越接近不稳定模态固有频率，离合器接合稳定性越差，振颤越显著；

(4) 阻力矩激励影响离合器摩擦振颤，激励频率越接近不稳定模态固有频率，振颤强度越大。而且，当阻力矩激励频率与接触压力波动频率相同时，二者同相位会加强振颤，而二者反相位会减弱振颤。

此外，发动机激励是传动系统扭振的主要激励源之一，发动机激励对离合器摩擦振颤的影响将在后续工作中进行。

参 考 文 献

[1] Crowther A,Zhang N,Liu D K,et al．Analysis and simulation of clutch engagement judder and stick-slip in automotive powertrain systems[J]．Proceedings of the Institution of Mechanical Engineers,Part D,2004,218(12)：1427-1446．

[2] Crowther A,Zhang N．Torsional finite elements and nonlinear numerical modelling in vehicle power-train dynamics[J]．Journal of Sound and Vibration,2005,284(3/4/5)：825-849．

[3] Centea D,Rahnejat H,Menday M T．Non-linear multi-body dynamic analysis for the study of clutch torsional vibrations (judder)[J]．Applied Mathematical Modelling,2001,25(3)：177-192．

[4] Centea D,Rahnejat H,Menday M T．The influence of the interface coefficient of friction upon the propensity to judder in automotive clutches[J]．Proceedings of the Institution of Mechanical Engineers,Part D,1999,213(3)：245-259．

[5] Duan C W,Singh R．Stick-slip behavior of torque converter clutch[J]．SAE Paper,2005,1：2456-2466．

[6] Duan C W,Singh R．Transient responses of a 2-dof torsional system with nonlinear dry friction under a harmonically varying normal load[J]．Journal of Sound and Vibration,2005,285(4/5)：1223-1234．

[7] Duan C W,Singh R．Super-harmonics in a torsional system with dry friction path subject to harmonic excitation under a mean torque[J]．Journal of Sound and Vibration,2005,285(4/5)：803-834．

[8] 胡宏伟，周晓军，杨先勇,等．离合器结合过程中抖动及其影响因素的分析[J]．浙江大学学报:工学版，2009，43(3)：535-539．

HU Hong-wei,ZHOU Xiao-jun,YANG Xian-yong．Analysis of clutch engagement judder and its influence factors[J]．Journal of Zhejiang University:Engineering Science,2009,43(3):535-539．

[9] 陈俐，王昊松，习纲．离合器接合过程抖振机理与控制研究[J]．系统仿真学报，2011，23(7)：1451-1458．

CHEN Li,WANG Hao-song,XI Gang．Clutch engagement control based on stability analysis[J]．Journal of System Simulation,2011,23(7):1451-1458．

[10] 颜克志，方宗德，张国胜．汽车离合器接合过程中的稳定性分析研究[J]．机械科学与技术，2007，26(5)：615-618．

YAN Ke-zhi,FANG Zong-de,ZHANG Guo-sheng．Stability analysis and study of automotive clutch engagement[J]．Mechanical Science and Technology for Aerospace Engineering,2007,26(5):615-618．

[11] Popov V L．Contact mechanics and friction physical principles and applications [M]．Berlin：Springer,2010．

[12] Astrom K J,Canudas De Wit C．Revisiting the LuGre friction model[J]．IEEE Control Systems Magazine,2008：101-114．

[13] Sinou J J,Dereure O,Mazet G B,et al．Friction-induced vibration for an aircraft brake system-part 1:experimental approach and stability analysis[J]. Journal of Mechanical Sciences,2006,48(5)：536-554．

Friction-induced vibration of wet clutches

YANG Li-kun, LI He-yan, MA Biao

(National Key Laboratory of Vehicle Transmission, Beijing Institute of Technology, Beijing 100081, China)

Abstract:The characteristics of friction-induced vibration of wet clutches were investigated based on a four-DOF dynamic model. The steady-state nonlinear LuGre friction model was employed. Stability analysis was performed by applying the eigenvalue method, the numerical simulation for the dynamic model was conducted with MATLAB/Simulink. The results demonstrated that the negatively sloped variation of friction coefficient with changes of relative sliding velocity and the fluctuation of interface pressure are the causes of clutch judder; under unsteady state, the larger the difference between static friction coefficient and kinetic one, the smaller the difference between the pressure fluctuation frequencies and unsteady modal frequencies, and the stronger the clutch judder; the resistance moment excitation has a similar effect to that of interface pressure fluctuation on clutch judder.

Key words:clutch judder; negatively sloped variation of friction coefficient; contact pressure fluctuation; the resistance moment excitation

基金项目：国家自然科学基金项目资助(51175042)

收稿日期：2014-12-30修改稿收到日期：2015-04-22

通信作者李和言 男，博士，副教授，1978年1月生

中图分类号:TH132.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.018

第一作者 杨立昆 男，博士生，1989年1月生

E-mail:lovheyan@bit.edu.cn