浮环密封运动机理及对轴系稳定性的影响

刘占生， 夏　鹏， 张广辉， 徐　宁

(哈尔滨工业大学 能源科学与工程学院，哈尔滨　150000)

浮环密封运动机理及对轴系稳定性的影响

刘占生， 夏鹏， 张广辉， 徐宁

(哈尔滨工业大学 能源科学与工程学院，哈尔滨150000)

摘要：浮环密封是引起轴系失稳的重要因素之一。建立浮环密封和转子瞬时运动关系，考虑温度影响，基于有限单元法求解瞬态流体动压力。利用摄动法求解锁死条件下浮环密封动力学系数，并与试验对比。结合非线性摩擦力和数值计算特点，提出浮环锁死动力学条件。建立浮环和转子耦合动力学模型，考虑瞬态流体动压力和摩擦力，研究浮环运动机理及相关因素。结果表明在小偏心率条件下，浮环负交叉刚度远大于主刚度；摩擦力越小、转速越高，锁死位置偏心率越小；锁死位置偏心较小时，浮环密封易引发轴系半频失稳现象，与工程实际相符合。

关键词：浮环密封；稳定性；瞬态响应；转子动力学

浮环密封是一种浮动式非接触密封，与固定式非接触密封相比，密封间隙更小，且具有自对心功能。因此，浮环密封不仅泄漏量少，而且不易发生动静碰摩。浮环密封被广泛应用于航空、舰船、航天领域的高速旋转机械动静流体密封，如燃气轮机中支承轴承油封、液体火箭发动机涡轮泵中液氧、液氢或煤油密封。然而，由于密封间隙较小，高速转子表面与间隙内流体相互作用比较强烈，易引起轴系失稳，成为高速转子系统稳定运行的关键技术问题。

针对浮环密封，国外学者先后做了大量的工作。San Andress等[2-3]利用bulk flow模型和改进模型，计算不同偏心率下浮环密封动力学系数，改进模型精度更高。Kirk等[4-6]基于Reynolds方程，研究油温、浮环周向槽结构及浮环受压变形对动力学系数的影响。Childs等[7-8]试验研究浮环周向槽结构形式和深度等因素对动力学系数的影响。上述研究假定浮环锁死于具体偏心位置，深入研究偏心率和浮环结构对动力学系数的影响，定性判断浮环对轴系稳定性的影响，但未对浮环运动规律和影响锁死位置的因素进行研究。Ha等[9]研究火箭涡轮泵中浮环密封锁死位置及动力学系数，但文中忽略流体动压力和摩擦力非线性特征及浮环运动过程，采用稳态平衡迭代方法计算锁死位置，不能反映浮环避免碰摩的运动机理。同时上述研究仅针对浮环自身，对于轴系失稳的原因和振动特征有待深入研究。

本文建立浮环-转子瞬时运动关系，求解瞬态流体动压力，并摄动求解动力学系数。与文献理论和试验结果对比，验证本文模型的正确性，研究锁死位置偏心率对动力学系数的影响。建立浮环-转子耦合动力学模型，考虑非线性瞬态流体动压力和摩擦力，研究浮环运动规律，阐明浮环避免碰摩的动力学机理，分析摩擦力、入口压力及转速对浮环运动过程和锁死位置的影响。参考燃机压气机结构，建立轴系有限元模型，研究浮环锁死位置对压气机轴系稳定性的影响。本文研究结论对浮环密封的设计和使用具有一定参考价值。

1理论模型及数值求解

1.1浮环密封动力学模型

工作中，具有转动限位装置的浮动密封会被两侧压差压紧在壁面上，仅做沿壁面方向的平动,如图1所示。基于牛顿定律，建立浮环动力学模型：

(1)

图1　浮环密封受力简图Fig.1 Force balance for a floating ring seal

1.2浮环-转子瞬时运动关系

图2　浮环-转子瞬时运动关系Fig.2 Floating ring-rotor transient motion relations

与固定约束的轴承不同，浮动环具有独立平动自由度。本文建立浮环与转子瞬时运动关系如图2所示。将笛卡尔基坐标系xOy放置于地面，则转子中心瞬时坐标为(xJ,yJ)，浮环中心瞬时坐标为(xS,yS)，计算可得浮环与转子瞬时偏心距e和偏位角φ。

1.3流体动压和动力学系数模型及数值求解

1.3.1瞬态流体动压模型

针对油介质工况，雷诺数Re<2 000，间隙内流体为层流，基于Reynolds方程和能量方程[10]，在坐标系rOJt中，建立间隙内流体压力和能量模型：

(2)

(3)

1.3.2动力学系数模型

(4)

将式(4)代入方程(2)合并整理得动力学系数方程：

(5)

1.3.3边界条件

入口压力边界，考虑Lomakin效应：

(6)

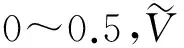
入口温度边界：

(7)

出口压力边界：

(8)

油膜空穴条件：

(9)

动力学系数边界条件，入口出口和空穴区域：

(10)

1.3.4数值求解

采用有限单元法求解瞬态油膜压力方程，对油膜沿周向和轴向划分矩形双线性单元，如图3所示。基于伽辽金变分原理，获得单元刚度矩阵和载荷矩阵，组成总体刚度和载荷矩阵。在周向施加周期边界条件，Pj,1=Pj,n,j=1～m+1，径向施加入口出口边界条件，采用SOR迭代求解。求解温度方程时，基于最小二乘变分原理，其它与求解油膜压力方程相同。采用直接迭代法求解压力和温度耦合非线性方程组，收敛条件为：

(11)

式中,Ui,j为节点压力或温度值，k为迭代次数。

求解动力学系数方程，与求解油膜压力方程方法相同。对结果量纲化获得P和Pi沿油膜分布，对P沿油膜积分获得油膜力，对Pi积分获得动力学系数。

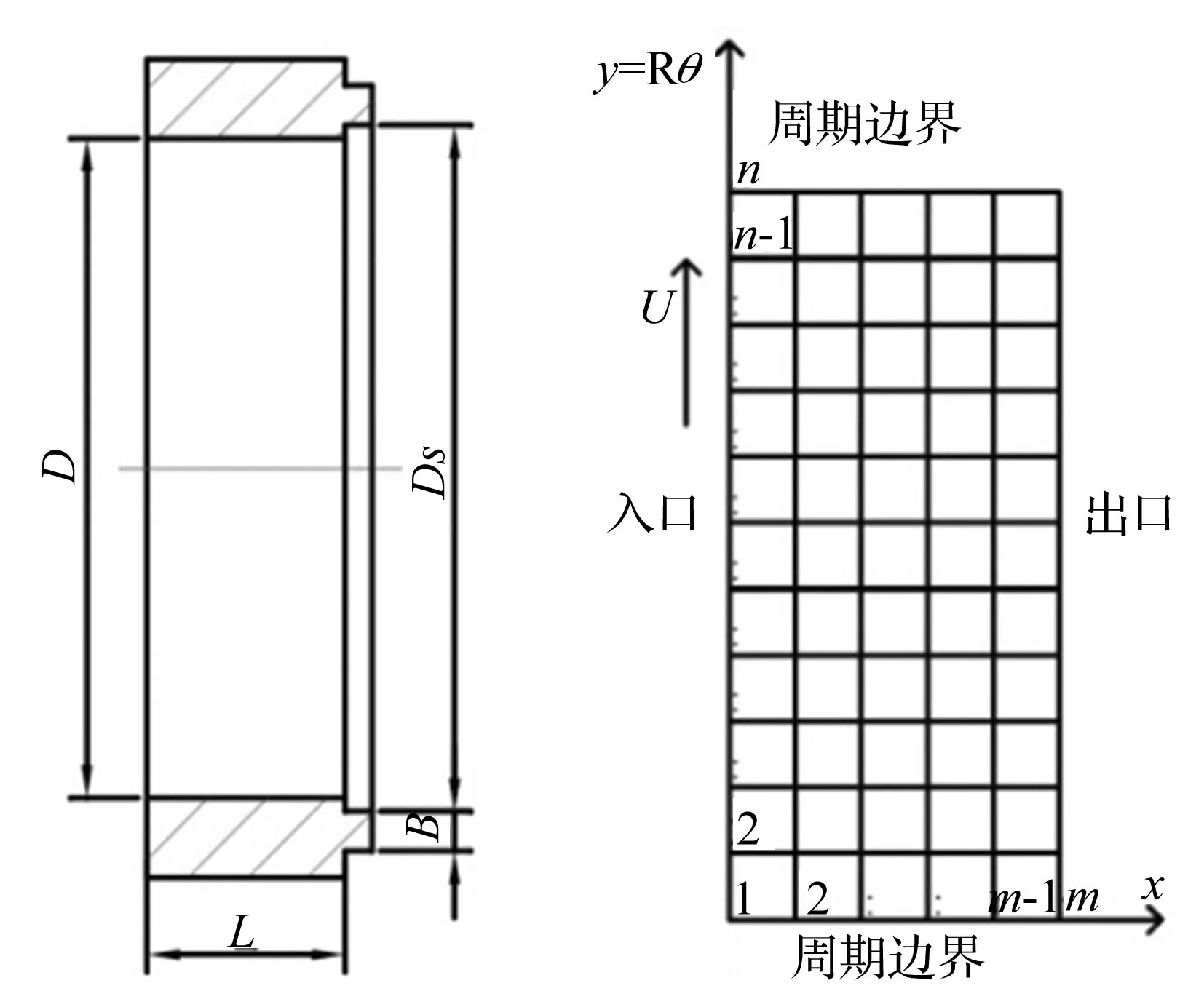
图3　浮环结构和油膜单元划分简图Fig.3 Floating ring seal structure and finite element mesh

1.4摩擦力模型和浮环密封运动锁死条件

壁面摩擦力与材料种类、相对速度等因素有关，本文考虑材料种类和相对速度对于壁面摩擦因数的影响[11]，采用库伦摩擦力模型：

(12)

(13)

根据摩擦力特性和数值计算特点，提出浮环运动锁死条件如下：

2) 满足条件1后，如流体动压力小于壁面摩擦力，根据静摩擦系数大于滑动摩擦因数规律，判断浮环锁死，锁死位置取相邻两时刻位移均值。

1.5浮环-转子非线性耦合系统模型及瞬态响应求解

采用Timoshenko梁单元，利用有限单元法获得浮环-转子系统非线性动力学方程。

(14)

式中,M为质量阵，C为阻尼矩阵，K为刚度矩阵，FB为轴承载荷，Fs为浮环密封力，Q为不平衡力，G为重力，z为广义位移矢量，表示[xi,yi,-θxi,θyi]T,xi,yi和θxi，θyi分别为转子上第i个节点沿水平和垂直方向的位移和偏转角。

采用Newmark数值积分方法对浮环-转子系统非线性运动微分方程进行求解，设计自适应步长控制算法，计算出系统在不同的参数状态下的动力学响应。

2动力学系数随偏心率变化规律及试验对比

Childs等[8,12]针对层流条件下浮环密封进行试验研究，主要研究偏心率对动力学系数的影响规律。密封结构参数和工况条件如表1所示。本文计算相应条件下动力学系数并与文献中理论和试验结果对比。

从图4(a)中本文结果可见，当ε<0.35时，随ε的增加，Kxx缓慢增大，当ε>0.35后，Kxx迅速增大。与文献理论结果能够很好吻合，当ε=0.56时，偏差最小为6.86%，当ε=0.04时，偏差最大为19.28%。与试验结果相比，当ε<0.35时，理论结果与试验结果能够较好吻合，但随偏心率增大，误差逐渐增大，当ε=0.72时，误差最大为49.72%。

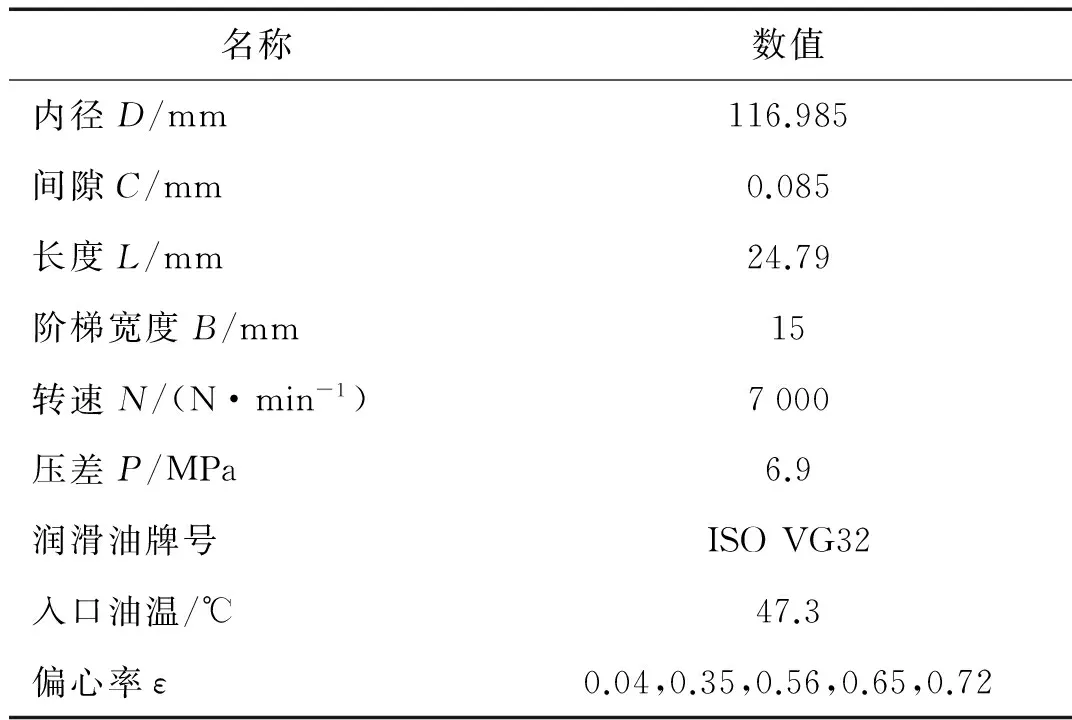
表1　浮环密封尺寸和试验参数

从图4(b)中本文结果可见，当ε<0.65时，Kyy非常小，接近于0，当ε>0.65后，逐渐增大，与文献理论结果变化趋势一致。与试验对比，当ε<0.35时，误差较小，但随ε增大，误差逐渐增大。

从图4(c)中本文结果可见，随ε增大，Kxy逐渐缓慢增加，然后减小。与文献理论结果能够很好吻合，当ε=0.56时，最大偏差为22.2%。与试验结果对比，当ε<0.35时，最大误差为22.6%，但随偏心率增大，误差逐渐增加。

从图4(d)中本文结果可见，Kyx为负刚度，随ε增大，逐渐减小。本文结果与文献理论结果能够很好吻合，当ε=0.35时，最大偏差为18.9%。当ε<0.35时，理论结果与试验结果能够较好吻合，但随偏心率增大，误差逐渐增大。对比图4(a)、(b)和(d)可见，当ε<0.35时，负刚度Kyx大于Kxx，远大于Kyy，降低轴系稳定性。

从图5(a)中本文结果可见，随ε增大，Cxx逐渐增加。与文献理论结果能够很好吻合, 当ε=0.35时，最小偏差为6.42%，当ε=0.04时，最大偏差为18.1%。当ε<0.56时，理论结果与试验结果变化趋势相一致，但当ε>0.56后，误差增大。

从图5(b)中本文结果可见，随ε增大，Cyy逐渐增加。与文献理论结果能够很好吻合, 当ε=0.72时，最小偏差为5.9%，当ε=0.32时，最大偏差为15.9%。与试验对比，理论结果变化趋势与试验一致，当ε=0.65时，最小误差为4.86%，当ε=0.72时，最大误差为14.8%。

图5(c)和图5(d)中，理论结果中Cxy等于Cyx，随ε增大，逐渐减小。本文结果与文献理论结果能够很好吻合。当ε=0.72时，最小偏差为9.21%。当ε<0.56时，理论结果与试验结果变化趋势相一致，但当ε>0.56后，误差增大。

图4　刚度系数随偏心率变化规律Fig.4 Stiffness coefficients versus eccentricity

图5　阻尼系数随偏心率变化规律Fig.5 Damping coefficients versus eccentricity

通过对比可见，本文理论结果与文献中理论结果能够很好吻合，证明文本理论模型和数值求解方法的正确性。当ε较小时，理论结果与试验结果变化趋势一致，但ε>0.56后，误差逐渐增大。本文认为，当ε较大时，由于试验工况密封背压为大气压，易引起空穴现象，与滑动轴承不同，雷诺边界条件不能较好模拟密封中空穴区域，引起较大误差。今后将利用CFD仿真研究浮环内空穴机理，修正理论模型。

3浮环密封运动机理及影响因素分析

浮环密封防止碰摩和自对心特性使其被广泛应用。基于本文瞬态模型，研究浮环运动机理及影响因素。

3.1浮环密封运动机理

实际中，浮环运动与轴系升速过程、供油压力和轴系振动等因素有关，本文瞬态模型可考虑上述因素计算浮环运动过程满足工程需要，但考虑众多因素不利于分析浮环运动机理。因此本文在定转速，定供油压力，轴系无残余不平衡量条件下，模拟即将碰摩工况，将浮环置于大偏心条件下ε=0.9，研究浮环运动过程，浮环尺寸和运行条件如表1所示。

从图6和图7可见，t=0时刻，流体动压力远大于壁面摩擦力。运动开始后，浮环速度快速增大，动压力迅速减小，当动压力减小到小于摩擦力时，浮环开始减速运动，动压力缓慢增加逼近摩擦力。当浮环运动速度减小到0.001 m/s后，摩擦力逐渐增加，浮环快速减速直至锁死。根据浮环运动过程可见，浮环由于惯性很小，能够快速跟随并超越转子涡动速度，削弱动压效应，导致流体动压力快速减小，直至与摩擦力相近，浮环处于沿壁面‘滑行’，因此可避免浮环与转子发生碰摩。浮环无量纲轨迹为图9中B=15曲线，可见浮环由初始位置ε=0.9，逐步向中心运动，锁死位置为ε=0.721，证明浮环具有自对心作用。

图6　油膜力和摩擦力随时间变化Fig.6 Film force and friction versus time

图7　浮环速度随时间变化Fig.7 Floating ring speed versus time

从图6和图7可见，浮环在启动和锁死运动过程中，力和速度剧烈变化，本文数值结果保证力和速度变化的连续性，证明瞬态模型计算方法是准确的。

3.2摩擦力、入口压力和转速对浮环密封运动的影响

分别研究摩擦力、入口压力和转速对浮环运动和锁死位置的影响，其中通过修改接触圆环宽度B，调整摩擦力；调整入口压力时，通过修改入口边界条件实现，摩擦力不变。

图8为不同摩擦力条件下浮环无量纲轨迹，可见摩擦力对于浮环运动有明显的影响，摩擦力越小，浮环运动距离越长，轨迹起始点切线方向与竖直方向夹角越大，锁死位置偏心率越小。当B=10 mm时，浮环由初始位置ε=0.9运动到锁死位置ε=0.601,而B=25时，锁死于ε=0.802 5。

图8　不同摩擦力条件下浮环运动轨迹Fig.8 Trajectory at different friction conditions

图9为不同转速条件下浮环无量纲轨迹，可见转速对于浮环运动有明显的影响，转速越大，浮环运动距离越长，轨迹起始点切线方向与竖直方向夹角越大，锁死位置偏心率越小。当N=8 000 N/min时，浮环由初始位置ε=0.9运动到锁死位置ε=0.689 4；N=5 000 N/min时，浮环锁死于ε= 0.774 2。

图9　不同转速条件下浮环运动轨迹Fig.9 Trajectory at different speed conditions

图10为不同入口压力下浮环无量纲轨迹，可见入口压力对于浮环运动有明显的影响，入口压力越大，运动距离越长，但入口压力对锁死位置偏心率影响较小，当Pin=7.7 MPa时，浮环由初始位置ε=0.9运动到锁死位置ε=0.718 8，当Pin=5.6 MPa时，浮环锁死于ε= 0.709 1。

图10　不同入口压力下浮环运动轨迹Fig.10 Trajectory at different inlet pressure conditions

4浮环密封对轴系稳定性的影响

参考国内某型燃机压气机结构，针对挤压油膜阻尼器失效时，轴系发生半频失稳现象进行研究。建立轴系有限元模型，利用本文瞬态模型计算浮环锁死偏心率为0.1～0.6，半径间隙比为0.000 2时，轴系升速1 000～13 000 N/min振动响应。轴系工作转速为11 500 N/min，一阶临界转速为5 348 N/min，二阶临界转速为13 826 N/min，振型如图11所示。

计算结果表明，当偏心率为0.1时，轴系在9 500 N/min开始发生失稳现象。图12为该工况下压气机第四级叶片节点处的振动响应，从图可见，随转速升高，半频幅值快速增大，且远大于相应基频幅值，轴系发生半频失稳现象，与工程实际相符合。然而当偏心率为0.2～0.6时，无半频失稳现象发生，证明当浮环密封锁死位置偏心率较小时，易引起轴系失稳。实际中，半径间隙是浮环密封重要的设计参数，本文进一步研究浮环密封锁死偏心为0.1时，半径间隙对失稳转速和工作转速下半频幅值的影响。图13为半径间隙比C/R=0.001～0.006条件下，失稳转速随半径间隙比的变化规律。从图可见，随间隙比的增大，失稳转速略有增加，当半径间隙比大于0.004后，无失稳现象发生，表明半径间隙越小，浮环密封降低轴系稳定性的影响越强。从图14可见，随半径间隙比的增大，工作转速下半频幅值迅速减小，半径间隙比越小，半频幅值衰减越明显。

图11　轴系一阶、二阶振型图Fig.11 The first and second mode

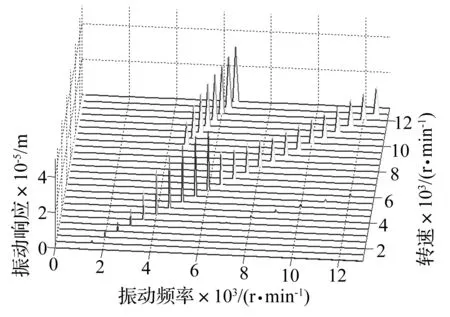
图12　转速升高轴系振动响应瀑布图Fig.12 Waterfall of vibration with speed increasing

图13　半径间隙比对失稳转速的影响Fig.13 unstable speed with radial clearance ratio

图14　半径间隙比对半频振动幅值的影响Fig.14 Half-frequency vibration amplitude with radial clearance ratio

5结论

通过本文研究，证明浮环密封具有自对心和防碰摩作用，但浮环锁死在小偏心条件下，降低轴系稳定性。主要结论如下：

(1) 在小偏心率条件下，浮环密封负交叉刚度远大于主刚度，降低轴系稳定性。

(2) 由于浮环惯性小，在流体动压力和摩擦力作用下，浮环沿壁面‘滑行’，能够快速跟随转子运动，避免碰摩现象。

(3) 摩擦力和转速对于浮环运动轨迹和锁死位置影响较大，摩擦力越小，转速越大，浮环锁死位置偏心率越小，然而入口压力对于锁死位置影响较小。

(4) 参考燃机压气机结构建模，证明当浮环锁死于小偏心率位置时，浮环易引发轴系半频失稳现象。

参 考 文 献

[1] Kirk R G.Oil seal dynamics:considerations for analysis of centrifugal compressor[C]//Proceedings of the 15th Texas A&M Turbomachinery Symposium,Kansas:Texas A&M University,1986:25-34.

[2] Semanate J E，Andres L S．Analysis of multi-land high pressure oil seals[J]．S T L E Tribology Transactions,1993，36(4):661-669.

[3] San Andres L，Delgado A．A novel bulk-flow model for improved predictions of force coefficients in grooved oil seals operating eccentrically[J]．Journal of Engineering for Gas Turbines and Power. 2012,134(5):0525091-05250910.

[4] Baheti S K,Kirk R G．Finite element thermohydrodynamic analysis of a circumferentially grooved floating oil ring seal[J]．S T L E Tribology Transactions,1995,38(1):86-96.

[5] Gordon Kirk R，Baheti S K．Evaluation of floating ring seals for centrifugal compressors using the finite element method[J]．Journal of Vibration and Acoustics,Transactions of the ASME,1999,121(1):131-136.

[6] Baheti S K，Kirk R G．Analysis of high pressure liquid seal ring distortion and stability using finite element methods[J]．J. Tribol.-Trans. ASME,1999,121(4):921-926.

[7] Childs D W，Rodriguez L E，Cullotta V，et al．Rotordynamic-coefficients and static (equilibrium loci and leakage) characteristics for short,laminar-flow annular seals[J].Journal of Tribology,2006,128(2):378-387.

[8] Childs D W，Graviss M，Rodriguez L E．Influence of groove size on the static and rotordynamic characteristics of short,laminar-flow annular seals[J]．Journal of Tribology,2007,129(2):398-406.

[9] Ha T W，Lee Y B，Kim C H．Leakage and rotordynamic analysis of a high pressure floating ring seal in the turbo pump unit of a liquid rocket engine[J]. Tribology International,2002,35(3):153-161

[10] 夏鹏．圆柱滑动轴承动静态特性分析及计算软件开发[D]．哈尔滨：哈尔滨工业大学，2013.

[11] Berger E J．Friction modeling for dynamic system simulation[J]．Applied Mechanics Reviews,2002,55(6):535-577.

[12] Graviss M S. The Influence of a central groove on static and dynamic characteristics of an annular liquid seal with laminar flow[D]. Kansas:Texas A&M University,2005.

Floating ring seals movement mechanism and its influence on stability of a rotor system

LIU Zhan-sheng, XIA Peng, ZHANG Guang-hui, XU Ning

(School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150000, China)

Abstract:Floating ring seals are one of important factors causing rotors to be unstable. Here, the relation between floating ring seals and rotor transient motion was established. The transient hydrodynamic pressure was solved with FEM considering thermal effect. The floating ring seals’ dynamic coefficients were solved with the perturbation method when the seals were locked, and they were compared with test results. Based on characteristics of nonlinear friction and numerical calculation, dynamic conditions for the locked-seals were proposed. Floating ring seals and rotors’ coupled transient dynamic models were established considering transient hydrodynamic pressure and friction to study the movement mechanism of seals and the corresponding factors. The results showed that under conditions of small eccentricity, the negative cross stiffness is much larger than the main stiffness; the smaller the friction, the higher the rotor speed and the smaller the eccentricity of the locked position; floating ring seals locked with a smaller eccentricity can cause oil-whip unstable phenomena in accordance with engineering experience.

Key words:floating ring seals; stability; transient response; rotor dynamics

基金项目：国家自然科学基金(11176010)

收稿日期：2014-12-11修改稿收到日期：2015-04-10

通信作者夏鹏 男，博士生，1986年6月生

中图分类号:TB42

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.017

第一作者 刘占生 男，教授，博士生导师，1962年生