施扰建筑高度对主建筑层阻力影响的试验研究

葛　福， 顾　明

(同济大学 土木工程防灾国家重点实验室，上海　200092)

施扰建筑高度对主建筑层阻力影响的试验研究

葛福， 顾明

(同济大学 土木工程防灾国家重点实验室，上海200092)

摘要：利用刚性模型测压试验，研究了施扰建筑高度比变化对主建筑层阻力系数和层脉动阻力功率谱的影响规律。试验包含了3个并列位置，5个串列位置和3个斜列位置。分析结果表明，建筑物并列时，当间距比小于3.0时，高度比为1.3时的层平均阻力系数在某些层可能比高度比1.0时增大高达20%，层脉动阻力系数在高度比为1.3且间距比小于3.0时会略大于单体建筑，其余情况与单体建筑一致；建筑物串列时，高度比对层平均阻力系数影响主要体现在遮挡效应上，高度比越大，遮挡效应越严重，遮挡高度越大，层脉动阻力系数由于遮挡效应减弱涡脱以及施扰建筑增加来流湍流共同作用，影响规律复杂，层脉动阻力功率谱的影响规律也表明了高度比越大影响高度越大；斜列工况的结果，表明了并列间距比对干扰规律起控制作用。

关键词：高层建筑；干扰效应；阻力；高度比；风洞试验

单体高层建筑顺风向风力已有很多研究，各国规范都给出了相关计算方法。但是在邻近高层建筑干扰作用下，受扰建筑的顺风向风力及其分布可能会与单体建筑截然不同。顾明等[1]总结了2003年以前的干扰效应研究成果，归纳了各个因素对干扰效应的影响规律。谢壮宁等[2-6]在干扰效应方面做得非常细致，研究的对象包含顺风向基底弯矩和基底弯矩响应，文中认为位于上游的高层建筑的静力干扰效应主要表现为 “遮挡效应”,且建筑物相距越近, 遮挡效应越严重。遮挡效应随施扰物体的宽度和高度的增加而增大, 但当高度比超过1.25后, 静力干扰效应基本不再变化, 可以忽略高度比小于0.5的施扰物体的干扰影响。陈素琴[7-9]利用数值方法研究了串列和并列建筑的干扰效应，给出了干扰下的流场分布。韩宁等[10-12]研究了受扰建筑局部风压的干扰特性，文中指出：串列布置时，高度比变化，当间距比小于3.0时高度比越大，对迎风面平均风压越不利，侧风面和背风面的平均风压均在等高时取得最小值；当间距比大于3.0时，受扰模型各个面的平均风压均随高度比的增大而减小；脉动风压随高度比的变化和平均风压不同，当间距比小于3.0时，受扰模型迎风面和侧风面脉动风压系数干扰因子均在等高时取得最大值；当间距比大于3时，迎风面和侧风面的脉动风压均随高度比的增大而增大，但背风面脉动干扰因子无论间距如何变化，均在高度比等于1.0时取最小值。

目前关于建筑物气动干扰的研究主要集中在基底力、基底力响应和局部风压方面，也有少量的气弹模型试验研究。以建筑物受到的层风力为对象来研究干扰效应，可以清楚地了解受扰下建筑受到的风力及其分布情况，是对前人所做干扰工作的补充和发展。但是，除了笔者的工作[13-15]外，尚未见对高层建筑层风力的干扰特性研究。笔者已经对施扰建筑与受扰建筑等高，施扰建筑位置变化下的层风力干扰效应进行了详细研究，得到了一些干扰规律[13-15]。本文进一步研究施扰建筑相对高度变化对受扰建筑层阻力系数和层脉动阻力功率谱的影响。

1试验安排

图1　施扰模型位置布置图Fig.1 Arrangement of buildings and coordinate system

2施扰建筑高度比变化对阻力系数的影响

(1)

2.1建筑物并列时的阻力系数

试验包含了间距比为2.0、3.0、4.0三种并列施扰位置。并列间距比小于3.0时，η=1.0时层平均阻力系数比单体建筑略大，η=0.7的层平均层力系数与η=1.0基本相似，η=1.3时层平均阻力系数比η=1.0大，某些层增大高达20%。分析发现这是因为干扰时背风面平均层力系数都比单体建筑大，且随高度比增大而增大，迎风面平均层力系数η=1.3时比单体建筑大，η=0.7与η=1.0接近且略小于单体建筑。并列间距比为4.0时，施扰建筑的存在会使得受扰建筑的平均层阻力系数稍微增大，高度比越大，增大越多，这主要是因为背风面的平均层力系数随高度比增大而增大。

间距比小于3.0时，η=0.7和η=1.0的层脉动阻力系数基本一致且与单体建筑接近，η=1.3的层脉动阻力系数比η=1.0增大约10%～20%；间距比为4.0时，各个高度比下的层脉动阻力系数与单体建筑几乎相等。

图2　并列间距比为3.0时层阻力系数随高度比变化图Fig.2 Layer drag force coefficients of diffirent hight ratio when side by side spacing ratio is 3.0

图3　并列间距比为4.0时层阻力系数随高度比变化图Fig.3 Layer drag force coefficients of diffirent hight ratio when side by side spacing ratio is 4.0

2.2建筑物串列时的阻力系数

试验包含了间距比为2.0、3.0、4.0、6.0、8.0五种串列施扰位置，各个位置的阻力系数随施扰建筑高度比的变化见图4～图8。

由图4(a)可知，间距比为2.0时，η=1.0时0.8H以下层平均阻力系数随层高变化很小，0.8H以上，层平均阻力系数随层高增大而接近单体建筑；η=0.7时各层平均阻力系数值比η=1.0时大；η=1.3时，层平均阻力系数随层高变化不大，各层平均阻力系数比η=1.0时小，最小为-0.22左右。

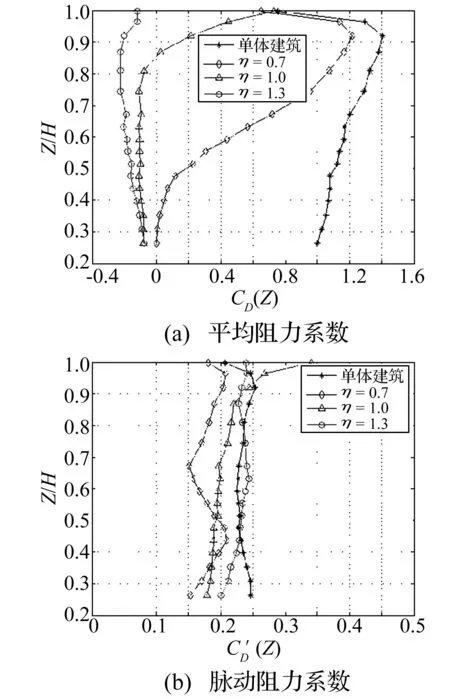
图4　串列间距比为2.0时层阻力系数随高度比变化图 Fig.4 Layer drag force coefficients of diffirent hight ratio when tandem spacing ratio is 2.0

由图4(b)可知，间距比为2.0时，η=1.0时的层脉动阻力系数除顶部外均小于单体建筑，η=0.7时，大部分层的脉动阻力系数都比η=1.0小；η=1.3时，除顶部外，各层脉动阻力系数都比η=1.0大，与单体建筑接近。

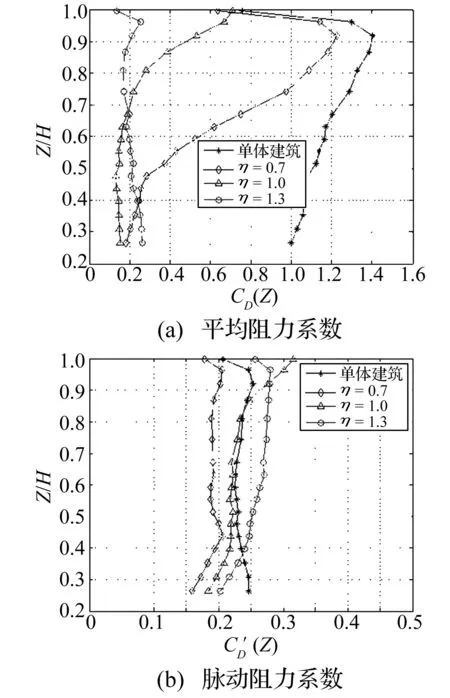
图5　串列间距比为3.0时层阻力系数随高度比变化图Fig.5 Layer drag force coefficients of diffirent hight ratio when tandem spacing ratio is 3.0

由图5(a)可知，间距比为3.0时，η=1.0时层平均阻力系数沿高不变的临界高度降低到0.6H；η=0.7的层平均阻力系数从底层开始就随层高增大而接近单体建筑，上部层平均阻力系数大于η=1.0的值；η=1.3时，层平均阻力系数随层高变化很小，值在0.2附近，上部层平均阻力系数小于η=1.0的值。图5(b)表明，一般地，高度比越大层脉动阻力系数越大，仅顶层η=1.3的层脉动阻力系数小于η=1.0的值，η=1.3时多数层的脉动阻力系数比η=1.0大20%左右。

图6　串列间距比为4.0时层阻力系数随高度比变化图Fig.6 Layer drag force coefficients of diffirent hight ratio when tandem spacing ratio is 4.0

图6(a)与图5(a)平均阻力系数受高度比的影响规律相同，但是由于间距比增大，遮挡效应减弱，层平均阻力系数在数值上有所增大。从图6(b)可以看出，间距比增大到4.0后，干扰下的脉动阻力系数随高度比变化规律与前面截然不同。下半部各高度比的脉动阻力系数比较接近，都比单体建筑小；顶部脉动阻力系数差别较明显，η=1.0的脉动阻力系数最大，η=0.7的脉动阻力系数最小，η=1.3的脉动阻力系数居中略大于单体建筑。

图7　串列间距比为6.0时层阻力系数随高度比变化图Fig.7 Layer drag force coefficients of diffirent hight ratio when tandem spacing ratio is 6.0

图8　串列间距比为8.0时层阻力系数随高度比变化图Fig.8 Layer drag force coefficients of diffirent hight ratio when tandem spacing ratio is 8.0

图7(a)和图8(a)表明，间距比大于6.0后，高度比对平均阻力系数的影响依然显著。η=0.7时，遮挡效应最弱，各层平均阻力系数大于η=1.0的值；η=1.3下部层平均阻力系数与η=1.0相似，上部层平均阻力系数小于η=1.0的值。

当串列间距比大于4.0时，前后两个建筑都会产生涡脱，层阻力系数的脉动与来流湍流和自身涡脱关系密切。图7(b)表明，在0.7H高度以下，层脉动阻力系数的大小规律与平均阻力系数类似，表明此时阻力系数的脉动主要由自身涡脱贡献，遮挡效应越弱，层脉动阻力系数越大；0.7H高度以上，η=1.0由于顶部遮挡减弱，同时干扰使得来流湍流增大，层脉动阻力系数大于单体建筑，η=0.7时，受扰建筑顶部仍然有遮挡作用，层脉动阻力系数小于单体建筑，η=1.3时，一方面遮挡作用减弱涡脱，另一方面干扰增大来流湍流，层脉动阻力系数随层高增大而增大。

图8(b)与图7(b)中各高度比下的脉动阻力系数十分接近，仅η=0.7的顶部区域脉动阻力系数稍微增大一些，接近单体建筑，这是因为间距比增大，遮挡减弱。

比较图4～8中的(a)图，不难发现建筑物串列时高度比对层平均阻力系数的影响规律：层平均阻力系数的干扰效应主要由遮挡作用引起，串列间距比越小，遮挡效应越严重，施扰建筑高度比越大，遮挡效应越严重，受扰建筑受遮挡效应影响的高度越大。

由图4～8中的(b)图可知，在间距比小于4.0时，后面受扰建筑会抑制前方施扰建筑的涡脱，仅在受扰建筑后方形成尾涡[8-9]，层阻力系数的脉动部分主要受施扰建筑尾流影响，一般的，施扰建筑高度比越大，层脉动阻力系数越大。间距比大于等于4.0时，前后两个建筑都会形成涡脱，高度比的影响与间距比小于4.0时截然不同，一方面由于遮挡效应，受扰建筑背风面的脉动要减小，另一方面，施扰建筑尾流增大了迎风面的脉动，导致脉动阻力系数受高度比的影响规律复杂。

2.3若干斜列位置的阻力系数

试验包含了(3.0，2.0)、(4.0，1.0)、(5.0，2.5)三个斜列施扰位置。并列间距比对于层阻力系数的干扰规律起控制作用，并列间距比大于2.0时，各个高度比下的平均阻力系数与单体建筑基本相同，脉动阻力系数变化也不大，仅η=1.3时顶部脉动阻力系数略大于其他工况。图9给出了位置(3.0,2.0)时的层阻力系数。

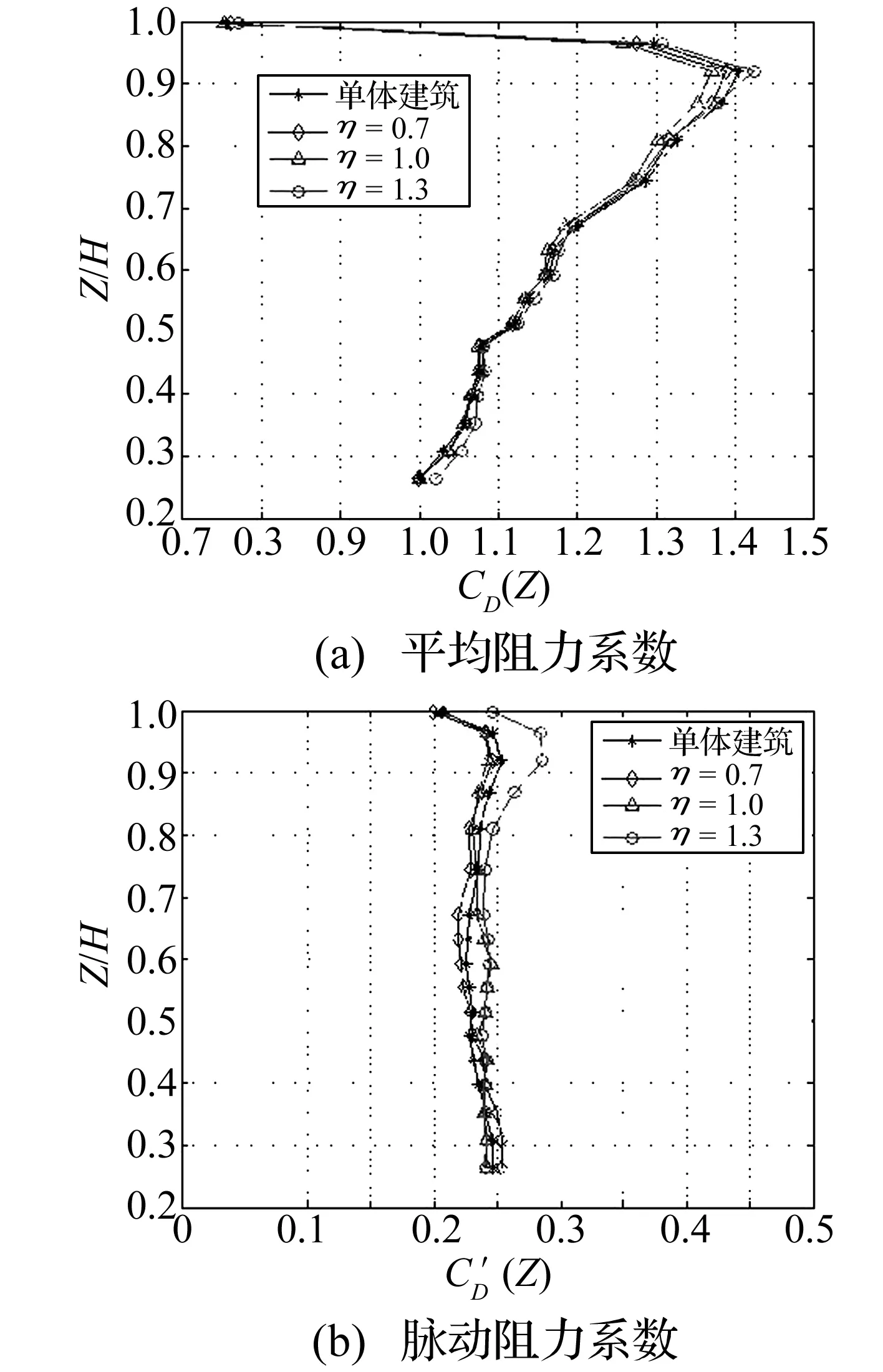
图9　位置(3.0，2.0)下层阻力系数随高度比变化图Fig.9 Layer drag force coefficients of diffirent hight ratio in position (3.0,2.0)

图10　位置(4.0，1.0)下层阻力系数随高度比变化图Fig.10 Layer drag force coefficients of diffirent hight ratio in position (4.0,1.0)

位置(4.0,1.0)下，由于并列间距比很小，平均阻力系数随高度比的变化情况与串列工况相似，高度比越大，遮挡效应越严重，上部层平均阻力系数越小。η=0.7的层脉动阻力系数小于η=1.0；η=1.3的层脉动阻力系数与η=1.0相差不大，最大可比单体建筑增大约30%。

3施扰建筑高度比变化对脉动阻力功率谱的影响

模型沿高共有17层，选其中的第1、4、7、9、11、13、15、17层进行分析，各层对应的高度分别为最底层(0.265H)、0.4H、0.5H、0.6H、0.7H、0.8H、0.9H和最顶层(0.996H)。

3.1建筑物并列时的脉动阻力功率谱

试验包括了并列间距比为2.0、3.0和4.0三种并列工况。建筑物并列时，各个间距比下，受扰建筑各层脉动阻力功率谱随施扰建筑高度比基本无变化，与单体建筑基本一致。这是因为并列工况下，阻力谱的能量主要由来流湍流贡献。图11给出了并列间距比为3.0时的各层脉动阻力功率谱。

3.2建筑物串列时的脉动阻力功率谱

试验包括了串列间距比为2.0、3.0、4.0、6.0和8.0五种串列工况。不同间距比下，层脉动阻力功率谱随高度比变化见图12～15。

串列间距比为2.0时，η=1.0各层脉动阻力功率谱峰值频率比单体建筑大。η=0.7时，在第11层(0.7H)以下，各高度比的谱峰值频率与η=1.0相似，在第11层(0.7H)以上，层脉动阻力功率谱与单体建筑基本一致。η=1.3的层脉动阻力功率谱峰值频率与η=1.0基本相同。

串列间距比为3.0时，第9层(0.6H)以下各高度比的谱峰值频率一致；第9层(0.6H)以上，η=1.0和η=1.3的脉动阻力功率谱峰会有两个峰值，η=0.7的脉动阻力功率谱与单体建筑基本一致。最顶层由于三维流效应，各个高度比下的脉动阻力功率谱与单体建筑基本一致，后面间距比继续增大时，最顶层的脉动阻力功率谱也基本不随高度比变化。

串列间距比为4.0时的干扰规律与串列间距比为3.0时相似。值得注意的是，η=1.0时，第15层(0.9H)脉动阻力功率谱的第二个峰值很小，间距比为6.0时，该峰消失。

串列间距比为6.0时，η=1.0时自第15层(0.9H)往上层脉动阻力功率谱与单体建筑基本一致，第15层以下，层脉动阻力功率谱峰值频率大于单体建筑。η=0.7时自第7层(0.5H)往上层脉动阻力功率谱与单体建筑基本一致，第7层以下与η=1.0类似；η=1.3时，第11层(0.7H)以下与η=1.0基本一致，第11层以上，层脉动阻力功率谱峰值大于η=1.0。

图11　并列间距比为3.0时层脉动阻力功率谱随高度比变化图Fig.11 Layer drag force spectrum of diffirent hight ratio when side by side spacing ratio is 3.0

图12　串列间距比为2.0时层脉动阻力功率谱随高度比变化图Fig.12 Layer drag force spectrum of diffirent hight ratio when tandem spacing ratio is 2.0

串列间距比为8.0时，η=1.0时自第13层(0.8H)往上层脉动阻力功率谱与单体建筑基本一致。η=0.7时自第4层(0.4H)往上层脉动阻力功率谱与单体建筑基本一致。η=1.3时，自第一层开始就出现多峰，这是因为间距比较大，前方施扰建筑尾流中的大漩涡分散成含能的小漩涡，造成阻力谱出现高频谱峰。分析η=1.3时迎风面的脉动层力谱，结果表明：迎风面由于施扰建筑的尾流作用，力谱谱值大，谱峰明显，尤其是在顶部，η=1.3下力谱谱值比单体建筑和其他高度比大很多，而且谱峰明显。

建筑物串列时的试验结果表明：施扰建筑的存在会使得受扰建筑层脉动阻力功率谱峰值频率变大或出现第二个峰值。η=1.0时，串列间距比较大时一定高度以上的层脉动阻力功率谱与单体建筑基本一致，这种现象在η=0.7时更明显；η=1.3时，各个间距比下受扰建筑各层(最顶层除外)的脉动阻力功率谱峰值频率都比单体建筑大或出现第二峰值。这表明，高度比不超过1.0时，施扰建筑可能不能完全遮挡受扰建筑，高度比为1.3时，施扰建筑可以完全遮挡受扰建筑(建筑物的间距比在试验包含范围内)。

3.3若干斜列位置的脉动阻力功率谱

试验包含了(3.0，2.0)、(4.0，1.0)、(5.0，2.5)三个斜列施扰位置。施扰建筑斜列布置时，受扰建筑处于施扰建筑的尾流中， 脉动阻力功率谱受施扰建筑的影响明显。η=1.0时，下部的层力谱峰值比单体建筑大，顶部受影响很小。η=1.3时，整个建筑的脉动阻力功率谱都受到影响，阻力谱峰值大于η=1.0，出现较高频谱峰。η=0.7时，层脉动阻力功率谱几乎不受影响。图16给出了位置(5.0,2.5)下的层脉动阻力功率谱。

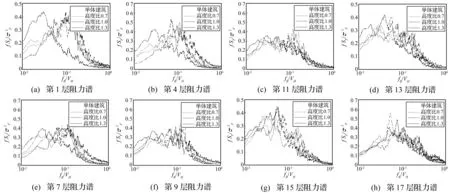
图13　串列间距比为3.0时层脉动阻力功率谱随高度比变化图Fig.13 Layer drag force spectrum of diffirent hight ratio when tandem spacing ratio is 3.0

图14　串列间距比为6.0时层脉动阻力功率谱随高度比变化图Fig.14 Layer drag force spectrum of diffirent hight ratio when tandem spacing ratio is 6.0

4结论

本文通过试验研究，比较了各个施扰位置下不同高度比的层阻力系数和层脉动阻力功率谱，并与单体建筑进行了对比。得到了一些高度比变化对受扰建筑层阻力的影响规律。

(1) 建筑物并列时，当间距比小于3.0，η=1.3时的层平均阻力系数在某些层可能比η=1.0时增大高达20%。层脉动阻力系数在高度比为1.3且间距比小于3.0时会略大于单体建筑，其余情况与单体建筑一致。建筑物并列时脉动阻力功率谱基本不随高度比变化，与单体建筑一致。

(2) 建筑物串列时，平均阻力系数的干扰效应主要是由于遮挡效应引起的，串列间距比越小，遮挡效应越严重，施扰建筑高度比越大，遮挡效应越严重，遮挡高度越大；在间距比为2.0时出现吸力，层平均阻力系数最小达到-0.22左右。间距比小于4.0时，高度比对脉动阻力系数的影响规律整体上是施扰建筑高度比越大，阻力脉动系数越大，某些位置由于施扰建筑的顶部三维流效应会略有变化。间距比大于4.0时，前后两个建筑都会形成涡脱，一方面由于遮挡效应，受扰建筑背风面的脉动要减弱，另一方面，施扰建筑尾流增大了迎风面的脉动，导致层脉动阻力系数受高度比的影响规律复杂。

图15　串列间距比为8.0时层脉动阻力功率谱随高度比变化图Fig.15 Layer drag force spectrum of diffirent hight ratio when tandem spacing ratio is 8.0

图16　位置(5.0，2.5)下层脉动阻力功率谱随高度比变化图Fig.16 Layer drag force spectrum of diffirent hight ratio in position (5.0,2.5)

(3) 建筑物串列时，不同高度比施扰建筑对主建筑脉动阻力功率谱影响不同，一般的，高度比越大层脉动阻力功率谱受影响的高度越大，谱峰值频率大或者出现多个峰值。

(4) 建筑物斜列时，并列间距比对于层阻力系数起控制作用。并列间距比大则高度比影响不明显，间距比小则影响规律类似串列布置。斜列时，受扰建筑处于施扰建筑尾流中，层脉动阻力功率谱的峰值和能量均受施扰建筑的影响。

参 考 文 献

[1] 顾明,黄鹏. 群体高层建筑风荷载干扰的研究现状及展望[J]. 同济大学学报:自然科学版,2003,(7):762-766.

GU Ming, HUANG Peng. Research history and state-of-art of interference effects of wind loads of a cluster of tall buildings[J]. Journal of Tongji University:natural science,2003,31(7):762-766.

[2] 谢壮宁,顾明,倪振华. 任意排列三个高层建筑间顺风向动力干扰效应的试验研究[J]. 工程力学,2005,(5):136-141.

XIE Zhuang-ning, GU Ming, NI Zhen-hua. Experimental study of along-wind dynamic interference effects among three arbitrarily arranged tall buildings[J]. Engineering Mechanics, 2005, 22(5):136-141.

[3] Xie Zhuang-ning,Gu Ming. Mean interference effects among tall buildings[J]. Engineering Structures,2004,26(9):1173-1183.

[4] Xie Zhuang-ning,Gu Ming. Simplified formulas for evaluation of wind-induced interference effects among three tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics,2007,95(1):31-52.

[5] 谢壮宁,顾明. 任意排列双柱体的风致干扰效应[J]. 土木工程学报,2005,(10):36-42.

XIE Zhuang-ning, GU Ming. Wind-induced interference effects between two arbitrarily arranged prisms[J]. China Civil Engineering Journal, 2005, 38(10): 32-38.

[6] 谢壮宁,顾明,倪振华. 三并列方柱风荷载特性的试验研究[J]. 西安交通大学学报,2003,(3):290-293.

XIE Zhuang-ning, GU Ming, NI Zhen-hua. Experimental study of wind load on three square prisms of side-by-side arrangements[J]. Journal of Xi An Jiao Tong University, 2003, 37(3):290-293.

[7] 陈素琴,顾明,黄自萍. 两并列方柱绕流相互干扰的数值研究[J]. 应用数学和力学,2000,(2):24-39.

CHEN Su-qin,GU Ming,HUANG Zi-ping. Numerical computation of the flow around two square cylinders arranged side by side[J]. Applied Mathematics and Mechanics,2000,21(2):131-146.

[8] 陈素琴,黄自萍,沈剑华,等. 两串列方柱绕流的干扰数值研究[J]. 同济大学学报:自然科学版,2001,(3):320-325.

CHEN Su-qin, HUANG Zi-ping,SHEN Jian-hua,et al. numerical computation of the flow around two square cylinders in tandem arrangement[J]. Journal of Tongji University:Natural Science,2001,29(3):320-325.

[9] 吴七二. 串列方形构筑物群绕流及其干扰效应的数值模拟[D].上海：上海交通大学,2011.

[10] 韩宁,顾明. 两并列方形高层建筑局部风压干扰特性[J]. 同济大学学报：自然科学版,2011,(10):1441-1446.

HAN Ning,GU Ming.Interference effects on wind pressure of two square tall buildings in side-by-side arrangement[J]. Journal of Tongji University:Natural Science, 2011,39 (10): 1441-1446.

[11] 韩宁,顾明. 两串列方形高层建筑局部风压干扰特性分析[J]. 土木建筑与环境工程,2011,(5):13-22.

HAN Ning,GU Ming. Characteristics of interference effects on local pressure of two square tall buildings in tandem arrangement[J].Journal of Cival,Architectural & Environmental Engineering,2011,33(5):13-22.

[12] 韩宁,顾明. 两串列方柱局部脉动风压干扰研究:第1部分 迎风面效应[J]. 振动与冲击,2009,(12):188-192.

HAN Ning,GU Ming. Interference effects on local fluctuating pressure of two square tall buildings in tandem arrangement:part 1 windward side effects[J]. Journal of Vibration and Shock, 2009,28(12):188-192.

[13] 顾明,葛福,韩宁. 方形高层建筑顺风向层风力干扰特性[J]. 同济大学学报:自然科学版,2014,42(5):665-671.

GU Ming, GE Fu, HAN Ning. Characteristics of along-wind layer wind force Interference effect of two square tall buildings[J]. Journal of Tongji University:Natural Science, 2014,42(5): 665-671.

[14] 顾明,葛福,韩宁. 方形高层建筑橫风向层风力干扰特性[J]. 同济大学学报:自然科学版,2014,42(8):1147-1152.

GU Ming, GE Fu, HAN Ning. Characteristics of across-wind layer wind force Interference effect of two square tall buildings[J]. Journal of Tongji University:Natural Science,2014,42(8):1147-1152.

[15] 顾明,葛福,韩宁. 施扰建筑高度对主建筑层升力影响的试验研究[J]. 同济大学学报:自然科学版,2015,43(2):181-188.

GU Ming, GE Fu, HAN Ning. Experiment study of impact of changes in the relative height of interfering building on main building layer lift force[J]. Journal of Tongji University:Natural Science,2015,43(2):181-188.

Tests for effects of relative height of interfering building on main building layer’s drag force

GE Fu, GU Ming

(State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Abstract:The effects of relative height of interfering building on main building layer’s drag force coefficients and drag force power spectrum were studied with rigid model pressure tests considering 3 side by side positions, 5 tandem positions and 3 oblique positions. The results showed that in side by side cases, the interfering building has little impact on the layer drag force coefficients and the drag force power spectrum; in tandem cases, the height ratio’s impacts on the mean layer drag force coefficients are mainly incarnated in shielding effect, the greater the height ratio, the more serious the shielding effect and the higher the shielding height; the interference law of the RMS layer drag force coefficients is complex because of the combination of shilding effect and increase in flow turbulence; the interference law of drag force spectrum also reveals the shielding height of different height ratio is different; the results of three oblique cases reveal across-wind spacing ratio plays a leading role in interference laws.

Key words:high-rise buildings; interference effect; drag force; relative height; wind tunnel test

基金项目：国家自然科学基金重大研究计划重点项目(90715040);集成项目(91215302)资助

收稿日期：2014-12-18修改稿收到日期：2015-05-20

通信作者顾明 男，博士，教授，博士生导师，1957年生

中图分类号:TU312.1;TU971

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.016

第一作者 葛福 男，硕士生，1989年生

E-mail: minggu@tongji.edu.cn