集成压电元件的挠性太阳帆板振动抑制控制系统

袁秋帆, 刘延芳, 马明阳, 齐乃明

(哈尔滨工业大学 航天工程系，哈尔滨　150006)

集成压电元件的挠性太阳帆板振动抑制控制系统

袁秋帆, 刘延芳, 马明阳, 齐乃明

(哈尔滨工业大学 航天工程系，哈尔滨150006)

摘要：针对基频低于1 Hz的大挠性太阳帆板，提出了整板主动振动抑制方法。该方法通过在太阳帆板上集成压电元件作为传感器和执行器；针对帆板挠性增大时，同位控制易出现虚假抑制的现象，综合考虑压电传感器的测量数据和板上一点的振动情况，基于正向位置反馈控制律(Positive Position Feedback,PPF)，设计了整板振动抑制控制系统。通过Adams和Simulink联合仿真，对控制系统的振动抑制能力进行了考核，结果表明所设计的PPF控制系统避免了虚假抑制，具有良好的整板振动抑制效果。

关键词：大挠性结构；振动抑制；正向位置反馈；整板抑制

航天探索的不断深入，对航天器提出大型化和轻质化的要求，太阳翼、天线等呈现越来越多的柔性；另一方面，高精度的对地定向和深空探测等应用需求又要求航天器具有高的姿态控制精度、小的振动扰动等。在航天器位姿机动或者稳定过程中，挠性附件的振动会影响航天器位姿控制及有效载荷功能，需要加以抑制。抑制方法可以分为被动和主动抑制方法。被动振动抑制[1]通过改变结构、增加阻尼材料，增大模态阻尼，将振动能量转化为其他形式的能量，达到振动抑制的目的，方法简单可靠，但灵活性低，抑制效果不明显。主动控制振动抑制方法可分为两种：一种是前馈控制方法，包括分力合成方法[2]和输入成型方法[3]；另一种是闭环反馈控制方法，根据传感器和执行器的不同又可分为两种方法，一种是是采用姿态传感器，实时测量本体由于挠性振动引起的姿态变化，通过一定的控制方法，消除振动，达到较高的姿态控制精度，比较典型的是模糊自抗扰控制[4]，第二种方法采用智能材料[5]，通过实时测量振动，再用执行器对挠性体施加作用力或力矩，达到振动抑制的目的，多采用分布黏贴的执行器布局形式，执行器作动器一般是压电陶瓷或者记忆合金等。主动振动抑制灵活性高，可以改变结构刚度和结构模态，有能力应对不断变化的外部环境(如负载变化或者形状变化)和内部环境(如损坏或故障)。采用贴压电陶瓷片实现主动振动抑制时，通常采用同位控制[6]，即压电执行器和压电传感器对位分别贴于薄板结构两侧，控制方法有速率反馈控制[7]、谐振控制[10]和正向位置反馈[11](Positive Position Feedback,PPF)等，近年来又有学者提出了H∞控制、LQG控制[8]和鲁棒模型参考控制[9]等。

文献[10]提出了谐振控制方法，该方法能够保证多输入多输出系统的闭环稳定性，并且在谐振频率处具有最大闭环阻尼，从而实现对结构特定模态振动的抑制,但其增加阻尼的能力是有限的。在此基础上，Fanson等[11]提出了正向位置反馈控制方法，该方法对于外溢效应不敏感，控制律设计简单，能够保证在系统结构带宽内存在不控制模态情况下的稳定性。

薄板柔性结构具有无穷阶谐振模态，是一个分布参数系统，每一阶模态都可以应用偏微分方程来描述。对挠性结构建模时，如果忽略了结构带宽之外的振动模态对结构整体振动的影响，这样虽然简化了控制器的设计，但这些忽略掉的振动模态会影响系统传递函数的零点，导致所设计的闭环控制系统不稳定。因此，Moheimani等[12]在系统传递函数中引入了馈通项作为对这部分的补偿，设计了相应的PPF控制器，对稳定性进行了重新推导。Moheimani采用悬臂梁试验验证了所设计的PPF控制律抑制结构振动的有效性。

在公开文献中，针对PPF控制律及其试验验证的研究所采用的薄板一阶频率一般在3 Hz以上，关于采用PPF控制律抑制1 Hz以内振动的相关报道却很少。然而，随着航天器的大型化和轻型化，下一代的航天器的挠性附件的基频往往在1 Hz以内，同位控制主动振动抑制易出现虚假抑制的现象[15]。因此，本文针对基频在1 Hz以内的太阳帆板进行了建模分析，应用PPF控制律的基本原理，提出以整板振动抑制为控制目标的控制系统结构，并设计了相应的PPF控制器，仿真试验结果表明所提出的整板振动抑制控制系统结构避免了虚假抑制，具有良好的整板振动抑制效果。

1集成压电元件的太阳帆板动力学模型

本节在对集成压电元件的挠性太阳帆板简化处理的基础上，建立其传递函数模型，并给出模型参数的辨识方法。

1.1传递函数模型

将太阳帆板简化为悬臂薄板，薄板表面任意位置(x1,y0)处两个侧面分别贴有一个压电陶瓷传感器和一个压电陶瓷执行器，压电元件施加在薄板上的载荷等效为力矩M(x,t)，施加位置如图1。

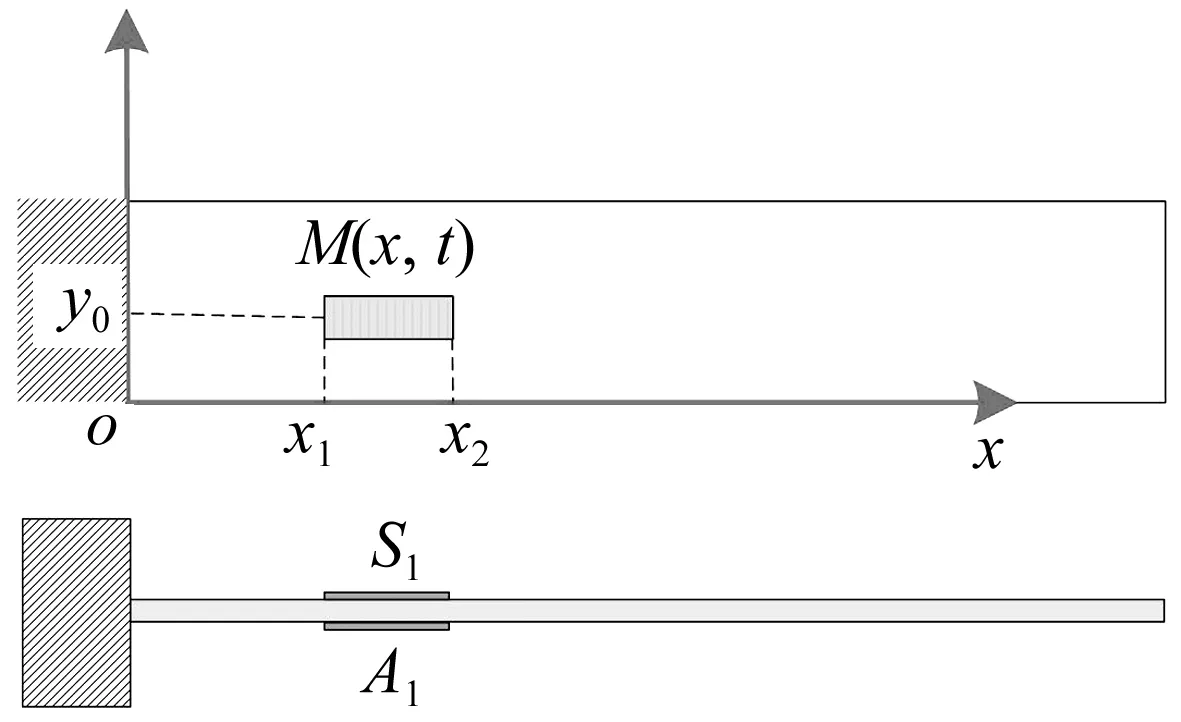
图1　集成压电元件的悬臂薄板模型Fig 1 Cantilever plate model with integrated piezoelectric element

应用经典基尔霍夫板理论，对于薄板使用动挠度来表示振动方程，定义板上动挠度为[13]：

(1)

式中，ωk为第k阶模态振型，qk为第k阶模态的广义坐标。

根据薄板振动基本方程和哈密顿原理，得到压电陶瓷输出力矩到动挠度的传递函数为[14]：

(2)

线性压电陶瓷用作传感器时，其模型为[12]：

(3)

式中：Cp为压电陶瓷片电容，Vs为电极间电压，Ep为材料的杨氏模量，ε1为x方向应变，wp为片长。

压电陶瓷执行器是利用逆压电效应输出微位移的执行器。应用经典基尔霍夫板薄板理论，可得对位粘贴压电陶瓷片的情况下，压电元件上施加的电压和产生的力矩的关系[12]：

T=EbIAd31Va/tp

(4)

式中：Eb为薄板的杨氏模量，tp为压电元件的厚度，I为薄板截面的惯性矩，d31为压电应变常数，A为与薄板和压电元件的杨氏模量与厚度相关的常数，该常数的计算公式因压电元件在薄板的粘贴方式不同而不同，对于同位控制，A计算公式如下:

(5)

对挠性薄板和压电陶瓷元件的数学模型进行整合，得到压电执行器输入电压到传感器输出电压的传递函数形式：

(6)

为了使控制系统可设计，将模态截断到第N阶，直接截断有可能导致外溢现象，从而导致控制系统不稳定。结构带宽内高于N阶的模态可以使用馈通项来近似，则控制系统开环传递函数可表示为：

(7)

模态截断误差项不影响开环传递函数的极点，但是影响开环传递函数的零点和闭环传递函数的极点，与系统是否稳定相关。

1.2模型参数辨识

薄板振动变形量为小量，多个执行器施加电压对单个传感器测量电压的影响满足叠加关系。同位控制时，设共有m对压电执行器/传感器对，则第i个执行器施加电压到第j个传感器测量电压的传递函数有如下形式：

(8)

Vi=K(ω0+vωt)j

(9)

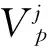
(10)

则如何求解传递函数参数的问题转化为以下数学问题：

已知函数形式为：

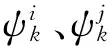
选取价值函数：

(11)

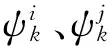
(12)

2控制系统设计

2.1控制系统结构

一般来说，薄板振动抑制控制系统以板根部的应力作为控制目标，使用压电传感器测量板根部的应力，控制器控制压电执行器，使板根部的应力快速衰减，但当基频较低时，板的挠性较大，在同位控制时，会出现虚假抑制的现象[15]，即在压电传感器上测量电压值迅速衰减，但板上除压电传感器位置外的其他位置仍然在振动，这样就达不到对板整体振动抑制的目的。

为了实现对板整体振动的抑制，选择板长中点的法线方向位移作为控制目标，控制系统的被控量是压电传感器的测量电压，控制量为压电执行器上的电压，设计控制器同时使该控制目标和传感器测量电压快速稳定，这样仅使用板上的压电元件实现了对板的整体振动的抑制。压电执行器与传感器配置方式如图2所示。挠性帆板所受到的干扰主要有中心刚体机动产生的作用力矩、太阳光压、摄动和执行器振动等，其中中心刚体机动带来的力矩干扰要远大于其他项，是挠性帆板振动的主要干扰源，因此，在挠性帆板上，使用一片压电执行器黏贴在帆板根部模拟中心刚体机动产生的力矩，作为干扰执行器，对板施加干扰力矩，量化干扰以便于对控制系统进行评价，另设置m对传感器执行器对，对板的振动情况进行采集，并对板施加作用力矩。

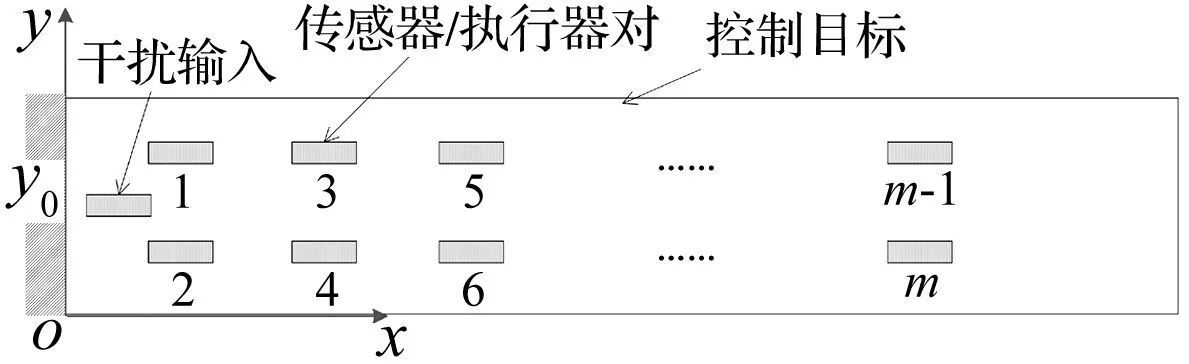
图2　控制系统组成Fig 2 Composition of control system

为了实现整板振动抑制的目标，提出整板振动抑制控制系统结构，如图3所示。

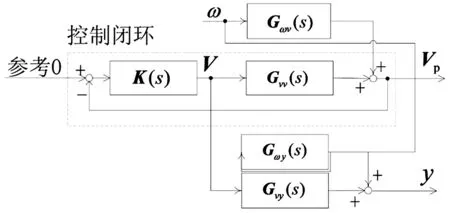
图3　控制系统框图Fig 3 Control system block diagram

控制目标为y，即板的中点位移， V为控制压电执行器输入电压，Vp为压电传感器测量电压，ω为干扰压电执行器输入电压，控制对象为Gvv(s)，控制器为K(s)。根据控制系统框图2可以得出，PPF控制器的作用是对干扰激发的控制目标y的振动进行反馈补偿，从而使控制目标尽快衰减。

2.2控制器设计

薄板结构振动的状态空间描述：

y=Cyx(t)+Dwyω(t)+DvyV(t)

Vp(t)=Cvx(t)+Dwvω(t)+DvvV(t)

(13)

式中：

PPF控制器的基本结构[11]为：

(14)

根据控制框图，PPF控制器的状态空间表达为：

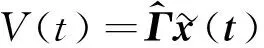
(15)

式中：

将Vp(t)代入式(16)得：

(17)

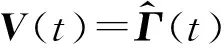
(18)

式中：

为证明PPF控制器的稳定性，需以下定理。

由m对执行器到m对传感器的传递函数Gvv(s)可以描述为：

Vp(t)=ψx(t)+DvvV(t)

(19)

式中：

PPF控制K(s)可以描述为：

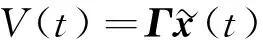
(20)

式中：

定理3.1[12]：假设Δ正定，由式(19)和式(20)构成的闭环负反馈系统稳定，当且仅当矩阵Q正定：

(21)

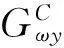
图4　极点配置Fig 4 Pole assignment

设计目标函数：

上述问题转化为：

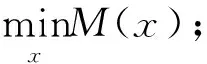
s.t.

(23)

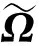
(24)

式中，κ是一个接近于1的常数。

3仿真分析

压电元件的粘贴位置如图2所示，板长2 450 mm，板宽270 mm，一号传感器执行器(S1A1)对位于板根部，二号传感器执行器(S2A2)对距离根部180 mm处，控制目标y位于距离根部1 250 mm处。根部中间对贴有两片压电元件，其中一片为三号执行器，用于提供干扰激励。控制目标为板上距离板根部1 250 mm的中点的沿Z正方向的位移量。控制目的是在有A3干扰输入时，使用S1A1和S2A2对板进行控制，使控制目标y的振动受到抑制。

仿真模型中，输入为施加在压电执行器上的等效力矩Ti，输出为压电传感器经过放大环节后的电压Vpi，i=1,2,…,m。

3.1模型参数辨识

根据所建立的模型，在压电执行器上加入适当的激励力矩，即一定带宽范围的扫频信号或者高斯白噪声，在压电传感器上获得表示结构响应的输出电压，对输出电压值进行傅里叶变换分析，可以获得模型每个模态的频率和阻尼。在已知传递函数结构的基础上，采用非线性拟合的方法，获取φk和D。

由执行器输入力矩到传感器输出电压的传递函数包含S1A1、S2A2两对压电元件，是一个二输入二输出的系统，再加上干扰力矩输入和控制目标y，如图。

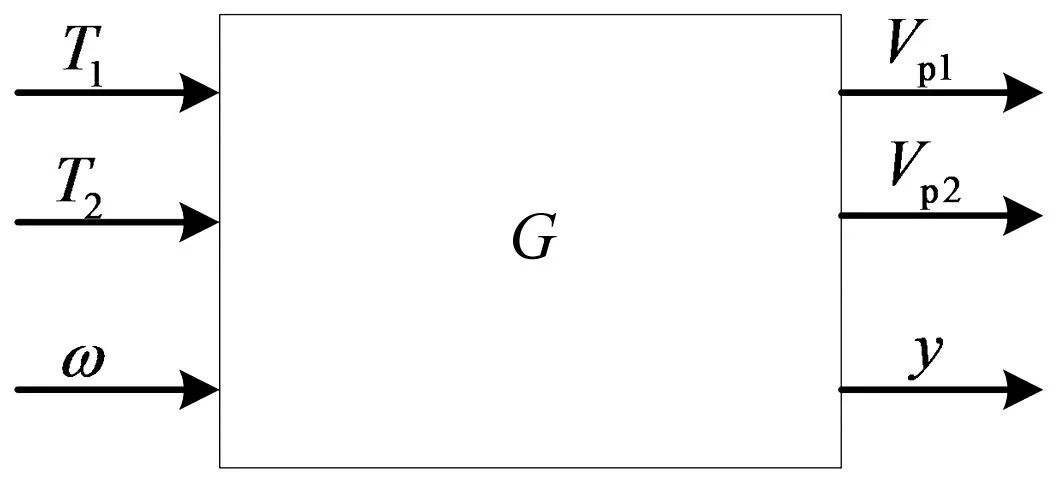
图5　传递函数Fig 5 The transfer function

G为传递函数矩阵，其形式为：

(25)

式中，Gij代表从Ai执行器到Sj传感器的传递函数，i,j=1,2,3。根据控制系统框图2-2，传递函数可分成四部分：

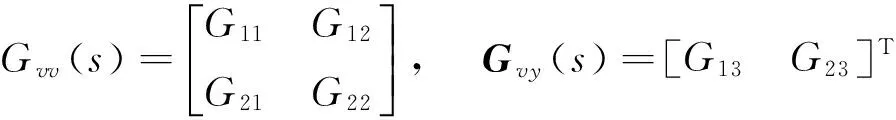
扫频输入力矩信号范围从0.1到3 Hz，施加到A1、A2和A3执行器上，得到S1、S2和y的输出，进而得到系统的幅频响应曲线，使用最小二乘非线性优化方法[19]求解传递函数参数。代入参数后的传递函数幅频响应曲线与原传递函数幅频响应曲线相比较，如图6所示。

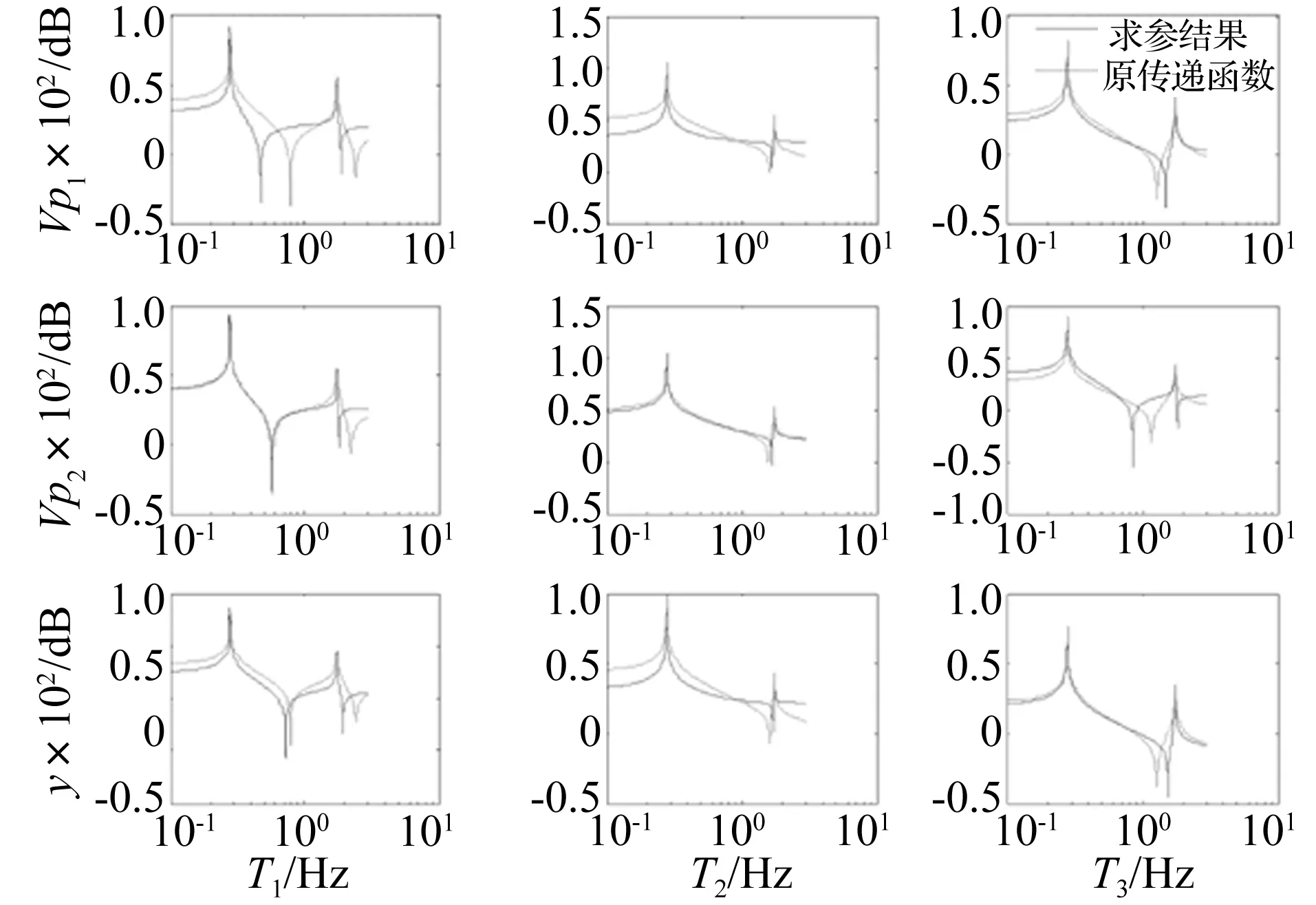
图6　传递函数优化求参结果Fig 6 Transfer function optimized results

3.2PPF控制器设计

使用极点配置法设计PPF控制器，根据系统开环传递函数可知系统开环极点为：

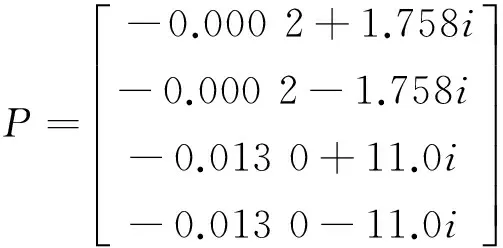
(26)

可见极点位置十分靠近虚轴，这样的系统阻尼很小，振动衰减较慢。利用式(22)的目标函数，在稳定性判断矩阵Q为正定的条件下，求解控制器的参数，使闭环控制系统的一对极点的实部向-1靠近，设计的闭环极点如图。

图7　PPF极点设计Fig 7 PPF pole design

由图可知，闭环控制系统将第一阶模态对应的极点向右配置，得到了两对虚部相近的极点，其中一对极点的实部接近-1的设计极点位置。闭环系统的极点为：

(27)

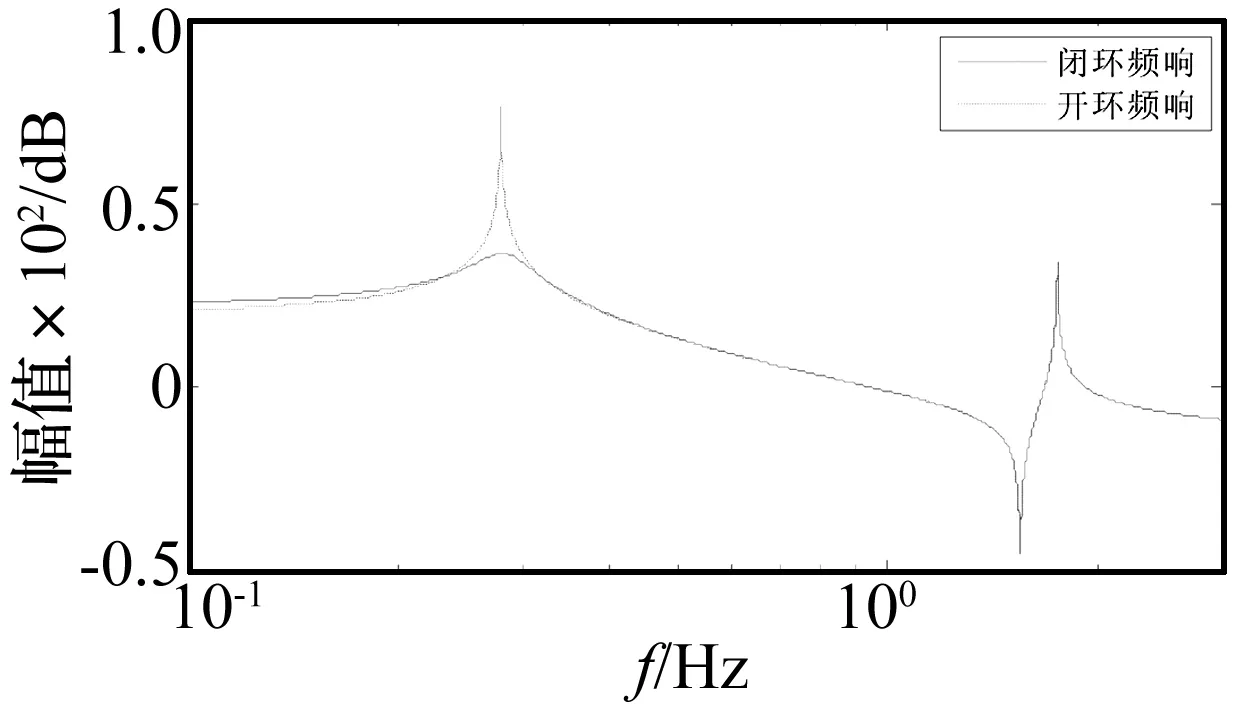
图8　闭环控制系统幅频响应Fig 8 Closed-loop control system amplitude frequency response

可见加入控制后，闭环传递函数在第一阶模态频率的增益大幅度减小。第二阶模态频率增益较小，设计的控制器没有针对该模态进行控制。

3.3仿真算例及结果分析

3.3.1仿真算例1

为了验证所设计的控制器的有效性，使用Adams建立集成压电元件的悬臂薄板模型，使用ADAMS/Simulink进行联合仿真，干扰输入信号为等效力矩：

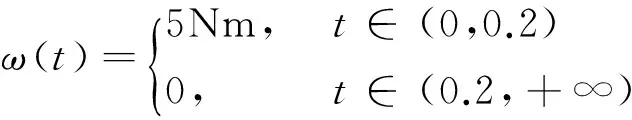
在初始0.2 s激发板自由振动。

板自由振动后，抑制和不抑制的板上压电传感器S1、S2和控制目标y的振动如图9～图11。

根据控制结果可以看出，不加控制时，y的第一阶模态振动明显，而且衰减较慢，闭环控制后，y的振动在30 s内衰减下来，第一阶模态振动被抑制，而更高阶模态在初始开始控制的前10 s内，被控制器轻微激振，之后由于结构自身阻尼，也很快衰减。

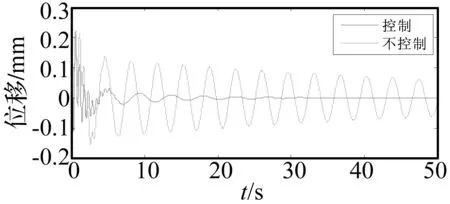
图9　控制目标y的位移Fig 9 Displacement of the control target y

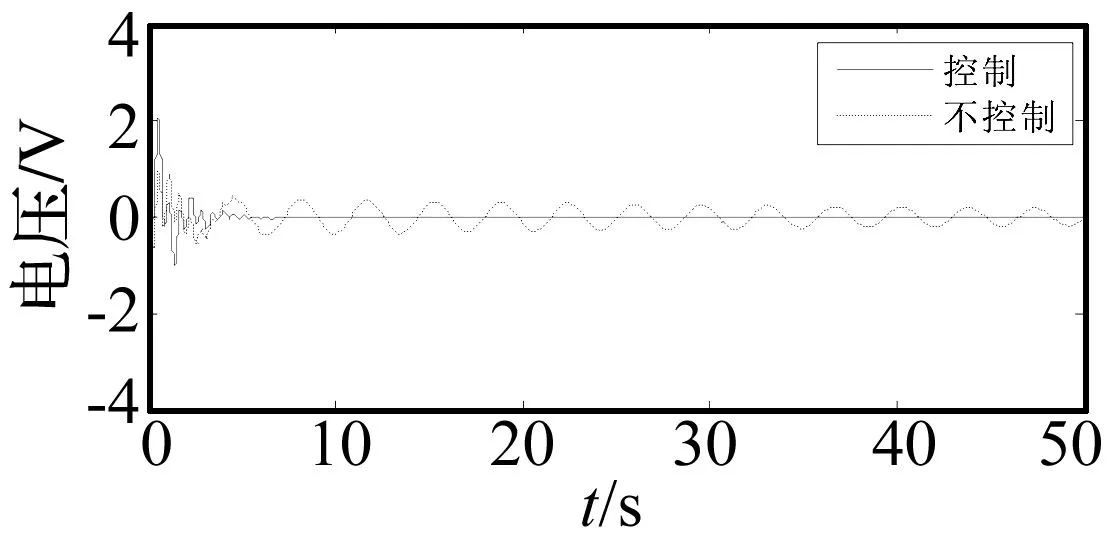
图10　一号压电传感器电压Fig 10 Voltage of sensor 1

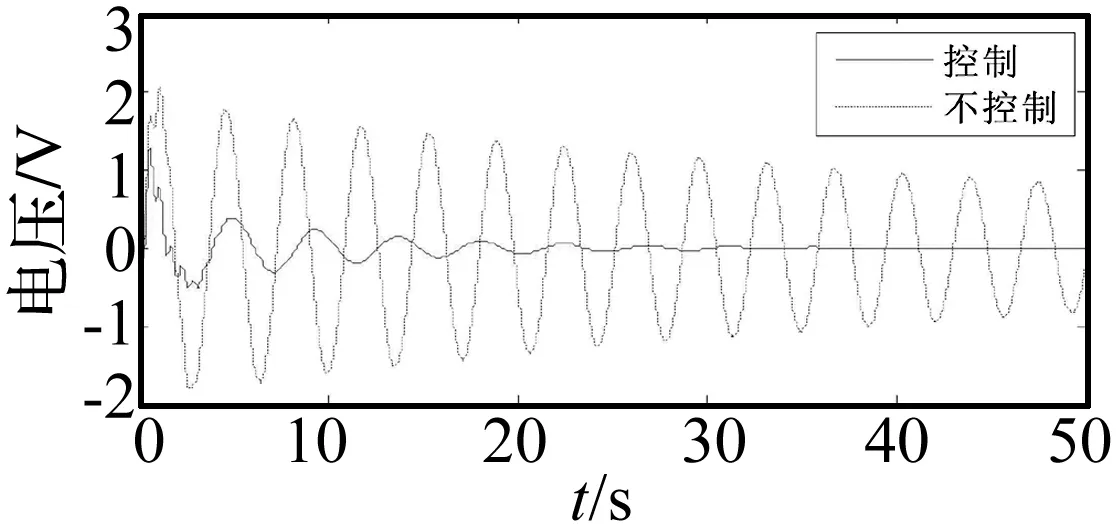
图11　二号压电传感器电压Fig 11 Voltage of sensor 2

对y进行快速傅里叶变换，如图12。

可见加入控制后，第一阶模态频率位置振动能量变小，证明控制器达到了振动抑制的效果。

一号执行器和二号执行器的控制力矩如图13和图14。

由于第一阶模态振型的应力变化最大位置在根部，一号执行器控制力矩远大于二号执行器的控制力矩。

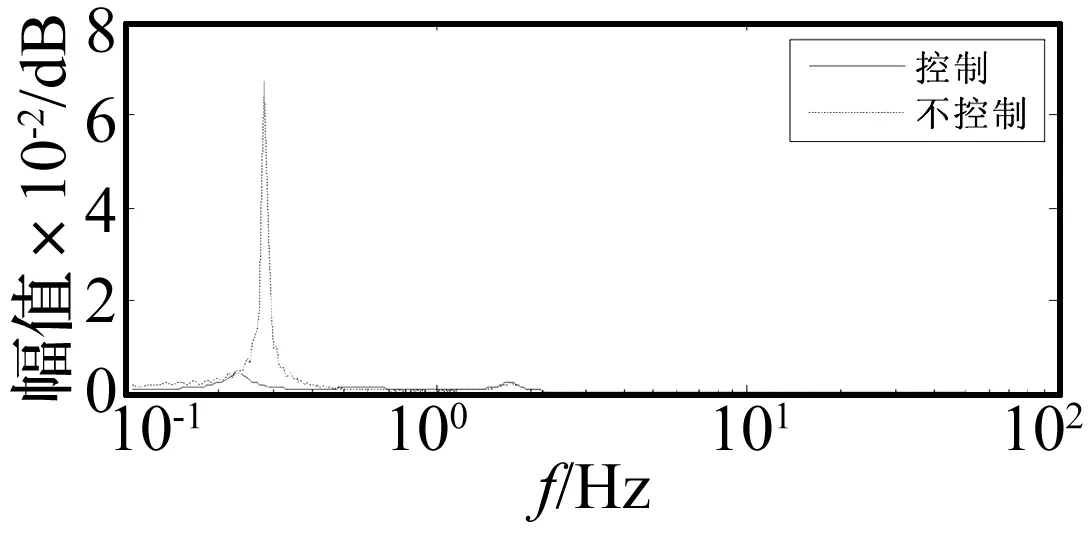
图12　控制目标y的频域分析Fig 12 Frequency domain analysis of control target y

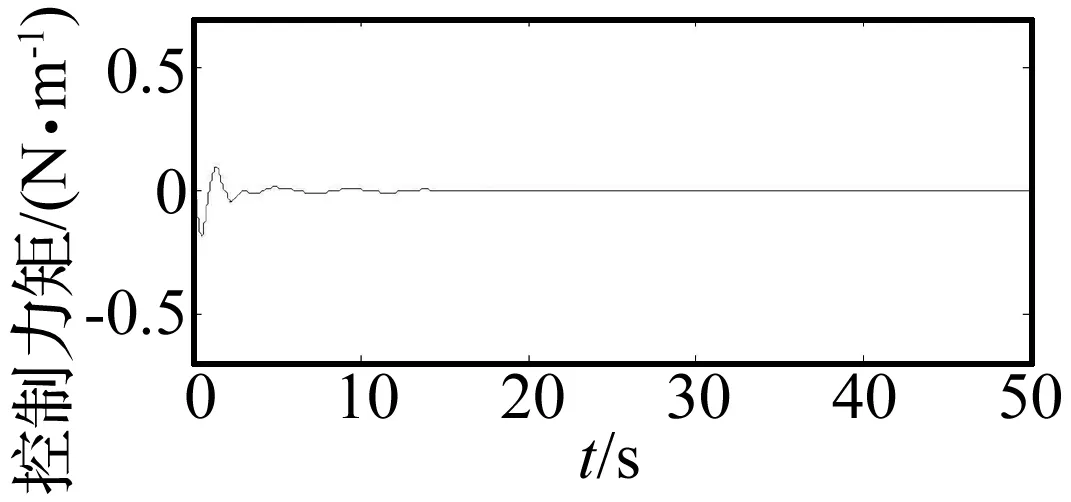
图13　一号压电执行器控制力矩Fig.13 Control torque of piezoelectric actuator 1

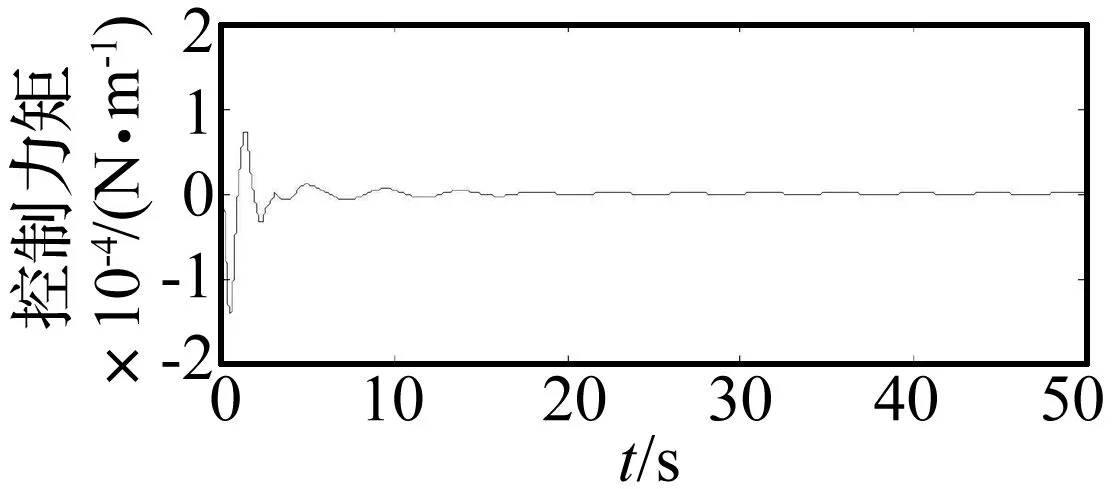
图14　二号压电执行器控制力矩Fig.14 Control torque of piezoelectric actuator 2

3.3.2仿真算例2

对更加一般的情况进行考虑，干扰输入信号设置为高斯白噪声，最大幅值5 Nm。板上压电传感器S1、S2和控制目标y的曲线如图15～图17。

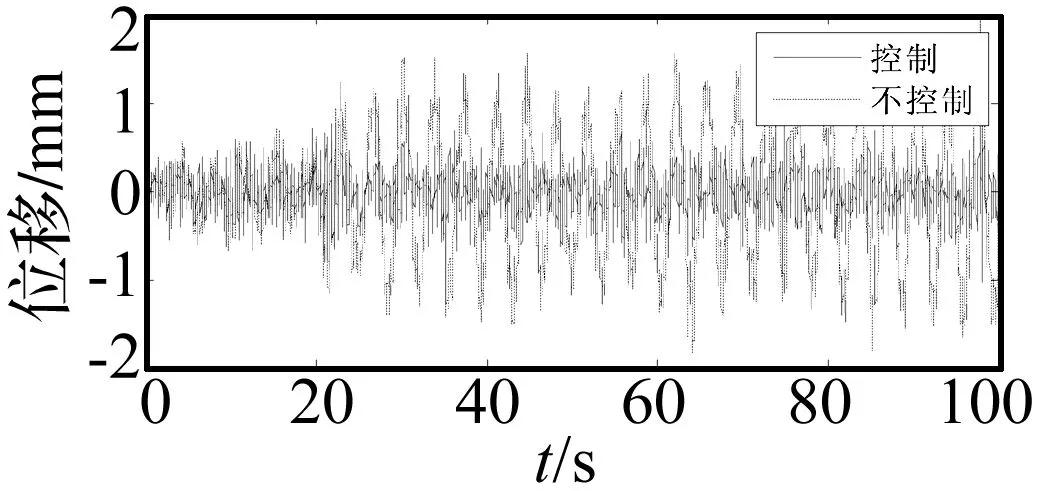
图15　控制目标y的位移Fig.15 Displacement of control target y

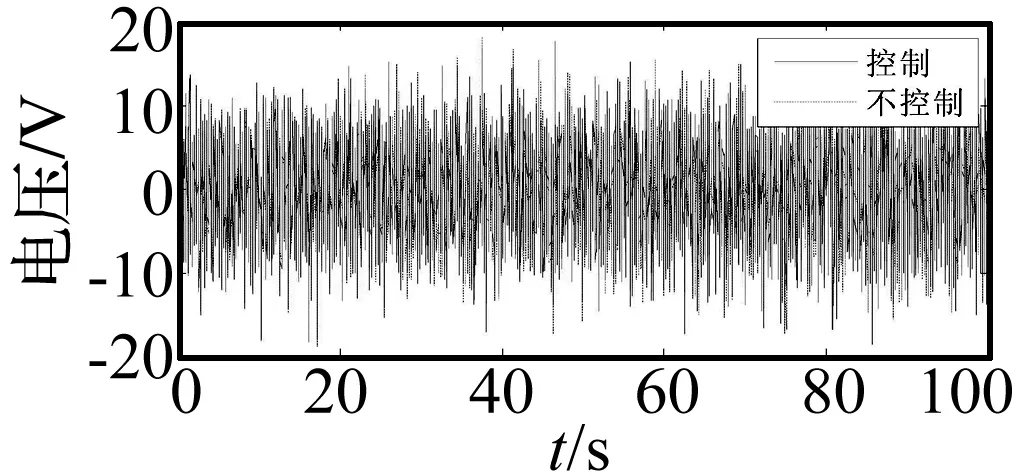
图16　一号传感器的电压Fig.16 Voltage of sensor 1

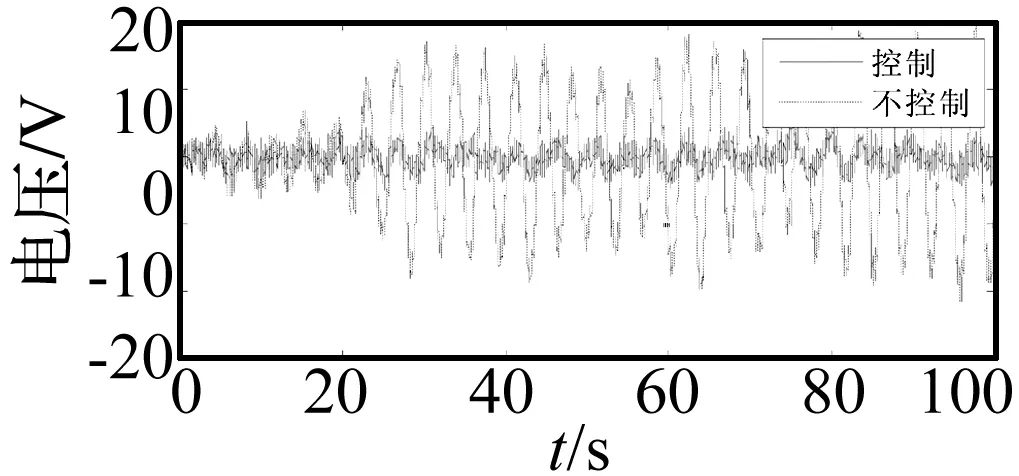
图17　二号传感器的电压Fig.17 Voltage of sensor 2

由图15～图17看出，不加控制时，在40 s后，控制目标的振幅y明显变大，板的第一阶模态振动被激发，加入控制后，控制目标y的第一阶模态振动被抑制。一号传感器上的电压在控制前后变化不大，这是由于干扰执行器与一号传感器竖直平行黏贴，又由于板较薄，根部以拉伸变形为主，干扰作用直接传递到了一号传感器。干扰作用主要通过板的弯曲振动传递到二号传感器。为了更加详细分析控制效果，对控制目标y和一号传感器输出电压进行fft变换，如图18和图19。

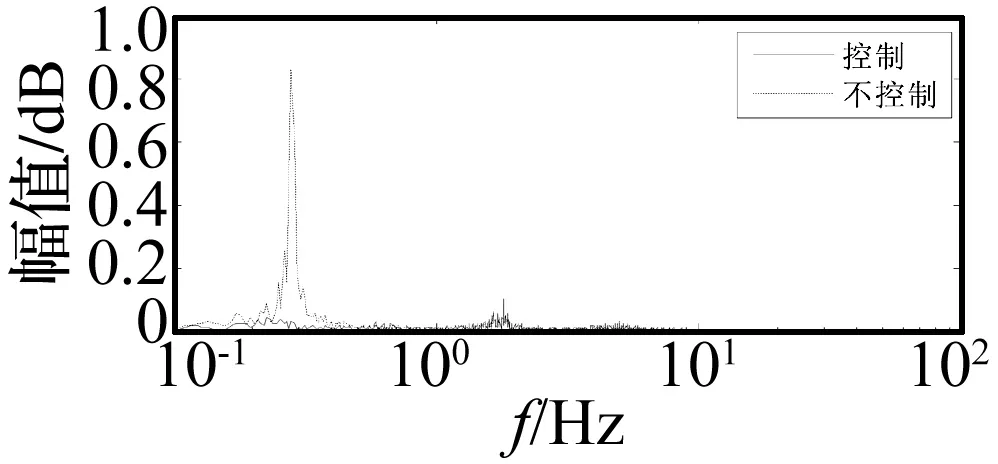
图18　控制目标y的频域分析Fig.18 Frequency domain analysis of control target y

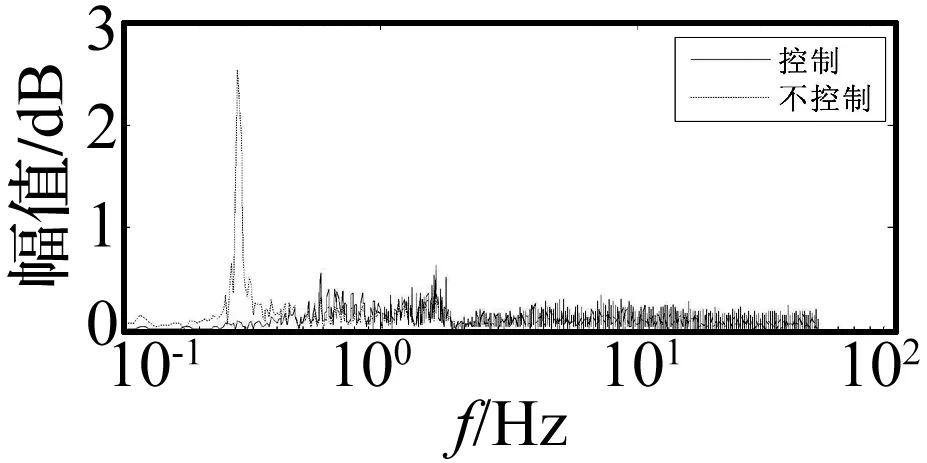
图19　一号压电传感器电压值的频域分析Fig.19 Frequency domain analysis of sensor 1 voltage

由图18和图19可知，y和一号传感器电压值在第一阶模态频率附近有很好的抑制效果。

4结论

本文针对集成压电元件的太阳帆板振动抑制控制技术进行了研究。首先建立了集成压电元件的悬臂薄板模型，基于经典基尔霍夫板理论，给出了压电执行器输入电压到传感器输出电压的传递函数，基于PPF控制律，提出了整板振动抑制控制系统结构。使用ADAMS/Simulink对设计的控制系统进行了联合仿真，结果表明所设计的控制器能够很好的实现整板振动抑制，根部的应力和板中部位移均较快收敛，提高了整板刚度。该方法具有潜在的应用前景。

参 考 文 献

[1] 杜华军,黄文虎,邹振祝. 航天支架结构的被动振动控制[J]. 应用力学学报,2002,19(3):10-11.

DU Hua-jun,HUANG Wen-hu,ZOU Zhen-zhu. Passive vibration control (PVC) of aerospace supporter[J]. Chinese Journal of Applied Mechanics,2002,19(3):10-11.

[2] 陕晋军,刘暾. 应用分力合成方法改善柔性系统性能的研究[J]. 系统仿真学报,2002,14(11):1536-1537.

SHAN Jin-jun,LIN Tun. Study on performance improvement of flexible systems using component synthesis method[J]. Journal of System Simulation,2002,14(11):1536-1537.

[3] 陕晋军,刘暾. 挠性结构的输入成型与分力合成主动振动抑制方法研究[J]. 中国机械工程,2002,13(5):379-383.

SHAN Jin-jun,LIU Tun. Study on input shaping and component synthesis method of flexible structure[J]. Chinese Journal of Mechanical Engineering,2002,13(5):379-383.

[4] 刘福才，陈鑫，贾亚飞，等.模糊自抗扰控制器在挠性航天器振动抑制中的应用[J].振动与冲击,2015,34(9):9-14.

LIU Fu-cai, CHEN Xin, JIA Ya-fei, et al. Application of Fuzzy Auto Disturbance Rejection Controller in Flexible Spacecraft Vibration Suppression[J]. Journal of Vibration and Shock,2015,34(9):9-14.

[5] 胡庆雷,马广富. 挠性航天器姿态机动控制的主动振动抑制[J]. 振动工程学报,2005,18(3):17-18.

HU Qing-lei,MA Guang-fu. Active vibration control of flexible spacecraft during attitude maneuver[J]. Journal of Vibration Engineering,2005,18(3):17-18.

[6] 陈勇,陶宝祺,刘果,等. 柔性结构振动控制的初步分析与试验研究[J]. 机械强度,1998,20(3):208-209.

CHEN Yong,TAO Bao-qi,LIU Guo,et al. Analysis and experimental study on the vibration control of flexible structures[J]. Journal of Mechanical Strength,1998,20(3):208-209.

[7] Balas M J. Feedback control of flexible systems[J]. IEEE Transactions on Automatic Control,1978,23(4):673-679.

[8] 袁国平,史小平,李隆. 航天器姿态机动的自适应鲁棒控制及主动振动抑制[J]. 振动与冲击,2013,32(12):110-115.

YUAN Guo-ping, SHI Xiao-ping, LI Long. Adaptive robust attitude maneuver control of a flexible spacecraft with active vibration suppression[J]. Journal of Vibration and Shock, 2013, 32(12): 110-115.

[9] 马天兵,裘进浩,季宏丽,等. 基于鲁棒模型参考控制器的智能结构振动主动控制研究[J]. 振动与冲击,2012,31(7):15-18.

MA Tian-bing, QIU Jin-hao, JI Hong-li, et al. Active vibration control of a smart structure based on robust model reference controller[J]. Journal of Vibration and Shock, 2012, 31(7): 15-18.

[10] Balas M J. Active control of flexible systems[J]. Journal of Optimization Theory and Applications,1978,25(3):415-436.

[11] Fanson J L,Caughey T K. Positive position feedback control for large space structures[J]. 1990,28(4):717-724.

[12] Moheimani S O R,Andrew J F. Piezoelectric Transducers for Vibration Control and Damping[M]. Germany:Springer,2006:9-66.

[13] Meirovitch L. Elements of vibration analysis[M]. McGraw-hill,Sydney,2nd edition,1996.

[14] Petersen I R,Lanzon A. Feedback control of negative imaginary systems[J]. IEEE Control Systems Magazine,2010,30(5):54-72.

[15] 李东旭,刘望,蒋建平,等. 空间智能桁架的传感器作动器位置优化和分散化自适应模糊振动控制[J]. 中国科学:技术科学,2011,41(5):605-606.

LI Dong-xu,LIU Wang,JIANG Jian-ping,et al. Placement optimization of actuator and sensor and decentralized adaptive fuzzy vibration control for large space intelligent truss structure[J]. Sci China Tech Sci,2011,41(5):605-606.

[16] Pereira E,Aphale S S. Stability of positive-position feedback controllers with low-frequency restrictions[J]. Journal of Sound and Vibration,2013,322:2900-2909.

[17] Fanson J L,Caughey T K. Positive position feedback control for large space structures[J]. 1990,28(4):717-724.

[18] Song G,Schmide S P,Agrawal B N. Experimental robustness study of position feedback control for active vibration suppression[J]. Journal of Guidance,2002,25(1):179-182.

[19] 陈震,薛定宇,郝丽娜,等. 压电智能悬臂梁主动振动最优控制研究[J]. 东北大学学报:自然科学版,2010,31(11):1550-1553.

CHEN Zhen,XUE Ding-yu,HAO Li-na,et al. On the optimal control of active vibration of a smart piezoelectric cantilever beam[J]. Journal of Northeastern University:Natural Science,2010,31(11):1550-1553.

Piezoelectric-based vibration control system for solar panels

YUAN Qiu-fan, LIU Yan-fang, MA Ming-yang, QI Nai-ming

(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)

Abstract:Here, an active vibration suppression method was proposed for flexible solar panels with first-order frequency less than 1 Hz. With this method, piezoelectric elements were employed and integrated into a solar panel as sensors and actuators. However, with decrease in the first-order frequency, the collocated control might cause unreal suppressions. To avoid unreal suppressions, both the measurement from sensors and the vibration of a point on the panel were taken into account in designing the positive position feedback (PPF) controller. The proposed method was validated with simulations based on Simulink and Adams. Results showed the effectiveness on vibration suppression of the whole panel.

Key words:high flexible structure; vibration suppression; positive position feedback; vibration suppression of the whole panel

基金项目：中央高校基本科研业务专项资金资助(HIT.NSRF.201622);CAST创新基金

收稿日期：2014-11-27修改稿收到日期：2015-04-30

通信作者刘延芳 男，博士后,讲师，1986年生

中图分类号:V414.33

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.014

第一作者 袁秋帆 男，博士，1992年生