分离式公铁双层桥面相互气动干扰及对列车走行性的影响

李永乐, 姜孝伟, 苏　洋, 李龙安, 廖海黎

(1. 西南交通大学 桥梁工程系，成都　610031； 2. 中铁大桥勘测设计院有限公司，武汉　430056)

分离式公铁双层桥面相互气动干扰及对列车走行性的影响

李永乐1, 姜孝伟1, 苏洋1, 李龙安2, 廖海黎1

(1. 西南交通大学 桥梁工程系，成都610031； 2. 中铁大桥勘测设计院有限公司，武汉430056)

摘要：横向风作用下公铁两用双层桥的上、下桥面间存在相互的气动干扰，为研究公铁两用组合桥间隔高度对列车走行性的影响，针对某分离式公铁两用混凝土箱梁桥，采用计算流体动力学(CFD)数值模拟和风-车-桥耦合振动研究的方法，分析了上、下桥面间隔高度对列车气动特性和车辆动力响应的影响。分析结果表明，公铁两用组合桥间隔高度对列车的气动特性和动力响应影响显著，间隔高度减小，列车升力系数和竖向加速度显著增大，轮重减载率也随之增大。公铁两用组合桥的设计应考虑间隔高度对列车的影响，以选择合理的间隔高度。

关键词：公铁两用桥；间隔高度；风-车-桥系统；走行性；CFD

列车在运行过程中受到侧风作用时，有可能发生侧滑、侧倾等安全问题，影响车辆的行驶安全[1]。相比于平地上，桥梁结构柔、离地高度大，车辆和桥梁间的耦合作用使行驶在桥梁上的列车更容易受到侧风作用的影响。杨明智[2]等通过风洞试验证明，在同样的运行速度和同样的大风风速下，列车在桥梁上运行比在平地上运行所受到的侧向力系数和倾覆力矩系数大，因而列车在桥上运行也相对较危险。

近年来，由于桥位资源限制以及经济性考虑，公铁两用双层桥面桥梁越来越受设计者们的青睐。横风在流经该类桥梁时，气流会在上层桥面和下层桥面处发生分离，形成上、下桥面各自的绕流。当上、下桥面高度间隔不足够大时，上、下桥面各自的绕流在上、下桥面之间的区域会产生相互干扰，并影响下层桥面车辆的气动特性。对于分离式公铁两用混凝土箱梁桥，因公路桥面和铁路桥面均为混凝土箱梁，梁高相对较大，上、下桥面气动绕流的相互干扰可能更为显著。

目前关于上下双层桥面间隔高度取值的研究较为少见，根据规范《标准轨距铁路建筑限界》的有关规定，间隔高度不得小于铁路建筑限界高度6.65 m[3]，这个高度未能充分考虑气动的影响。徐鹤寿等[4]则建议建筑限界的最大高度为7 m(该值为轨面以上的高度)，彭月燊等[5]建议建筑限界高度从轨面起算，在一般情况下定为7 m，但这个高度并未考虑公铁双层桥面间的气动干扰效应。此外出于经济性的考虑，设计中通常尽量减小公铁两用桥上、下桥面之间的高度，因此双层桥面间的气动干扰以及对下层桥面车辆的气动影响难以避免，但目前业界针对这一问题的研究较为少见。

本文以某分离式公铁两用混凝土箱梁桥为背景，采用CFD数值仿真软件FLUENT分析研究了上、下桥面间相互的气动干扰，明确了气动干扰对车辆风荷载的影响，并采用风-车-桥耦合振动分析的方法研究了气动干扰对车辆走行性的影响，讨论了上、下桥面不同间隔高度的影响，研究结论对实际工程具有指导意义。

1间隔高度对列车风特性的影响

1.1工程概况

某分离式公铁两用混凝土箱梁桥全长为1 216 m，每孔跨度32 m，共38孔，结构布置形式如图1所示，上层公路桥采用分离的独立主梁，设计为双线六车道，单幅桥面宽16 m。下层为双线铁路，桥面宽12.43 m。公路主梁通过高18m的支墩安置在刚度很大的下部桥墩上。为考察上、下桥面间隔高度的影响，本文共进行了8.3 m、10.7 m、13.1 m、15.5 m共4种高度间隔的对比分析。双层桥面间隔高度具体指公路主梁底面与铁路主梁上表面的距离，原设计中双层桥面间隔高度为10.7 m。因桥址区风环境较为恶劣，公路桥面设有1 m高的护栏以及2 m高的风屏障，铁路桥面设有2 m高的风屏障。

图1　公铁两用组合桥横断面(单位：mm)Fig.1 Cross section of highway-railway combined bridge (Unit: mm)

1.2CFD建模

文献[6-8]针对不同模型提出了较为合理的计算域尺寸，并指出对于桥梁这种长高比很大的结构计算域的宽度约为模型高度的4倍左右，计算域高度约为模型高度的7倍～10倍，模型距出口的距离约为高度的11倍～12倍。经多次试算，在考察区域无关性和网格无关性的基础上，综合考虑计算效率和计算精度，计算区域定为：横桥向宽440 m，竖向高220 m，模型距速度入口130 m。

数值分析中，湍流模型采用对复杂边界层分离流模拟比较有效的(SST)κ-ω湍流模型，该模型在壁面位置采用标准κ-ω模型，而在外层采用由标准κ-ε模型改进得到的κ-ω模型，结合了两者的优势，很适合于强压力梯度与分离下的复杂边界层流动[9]。对计算边界，迎风面设置为速度入口边界条件，入口风速取为30 m/s,湍流强度[10-11]取为0.5%，背风面采用压力出口边界条件，主梁断面和风屏障、栏杆均采用壁面边界条件，计算区域及边界条件见图2。划分网格时模型中心区域采用四边形非结构化网格，外围采用四边形结构化网格，网格数量约62万，网格划分如图3所示。

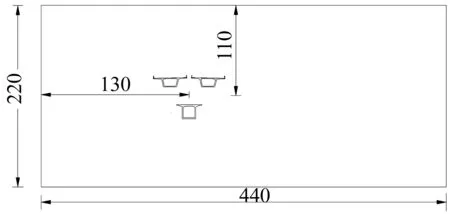
图2　计算区域和边界条件(单位：m)Fig.2 Calculating region and boundary condition (Unit: m)

图3　网格划分Fig.3 Calculating Mesh

不同模型的阻塞率分别为2.1%(单独公路桥)、3.3%(单独铁路桥)、7.0%(公铁组合桥)，与之相对应的雷诺数分别为：9.4×106、1.46×107、3.1×107，各模型的Y+值大多集中在300以内，基本满足相关要求。

1.3数值模拟结果

1.3.1桥梁及车辆的三分力系数定义[12]

(1)

式中：α为来流攻角，ρ为空气密度，H、B、L分别为桥梁或列车的高度、宽度和长度，FH(α)、FV(α)、FM(α)分别为不同攻角α情况下采用体轴坐标系时，结构物的侧向阻力、升力、扭矩。

1.3.2公铁桥面流场相互干扰

考察公路桥面和铁路桥面流场的相互干扰，采用原设计间隔高度(10.7 m)，分别建立了单独公路桥、单独铁路桥以及公铁组合三种模型(公路桥面设有1 m高的护栏以及2 m高的风屏障，铁路桥面设有2 m高的风屏障),对其进行CFD分析，得到三种情况下的流场风速云图，如图4～图6所示。从风速云图可以看出：公路桥和铁路桥组合情况下风速云图发生了较大变化,双层桥面间的风速增大明显，这表明上、下桥面间的流场存在明显的相互气动干扰现象。

图4　单独铁路桥流场风速云图Fig.4 Flow velocity cloud map at the case with only railway deck

图5　单独公路桥流场风速云图Fig.5 Flow velocity cloud map at the case with only highway deck

图6　公铁组合时流场风速云图Fig.6 Flow velocity cloud map at the case with the combined highway-railway bridge deck

1.3.3公路和铁路桥面气动力的相互影响

为进一步探讨公铁两用桥桥面之间的相互干扰，通过CFD定常分析计算桥梁截面的静风荷载[13]，并进一步计算单独公路桥、单独铁路桥、公铁组合三种状态下公路和铁路桥梁各自的气动力系数(如表1所示),分析中采用原设计间隔高度(10.7 m)。

由表可知，单独铁路桥面以及单独公路桥面的气动力系数均与组合情况下的有不同程度的差异。单独铁路桥的阻力系数较组合状态下的减小16.2%，单独公路桥(前幅，指迎风侧)的阻力系数较组合状态下的增大6.2%。单独公路桥(后幅，指背风侧)以及组合状态下的公路桥(后幅)由于公路桥(前幅)的阻挡作用，阻力系数均较小。单独铁路桥和公路桥(前、后幅)的升力系数较组合状态下的有所减小，最大减小幅度为27.8%。单独铁路桥和公路桥(前、后幅)的扭矩系数较组合状态下的有所减小。不同组合状态下公路桥面和铁路桥面气动力系数的差异也间接表明公路和铁路桥面之间存在着显著的相互气动干扰现象。

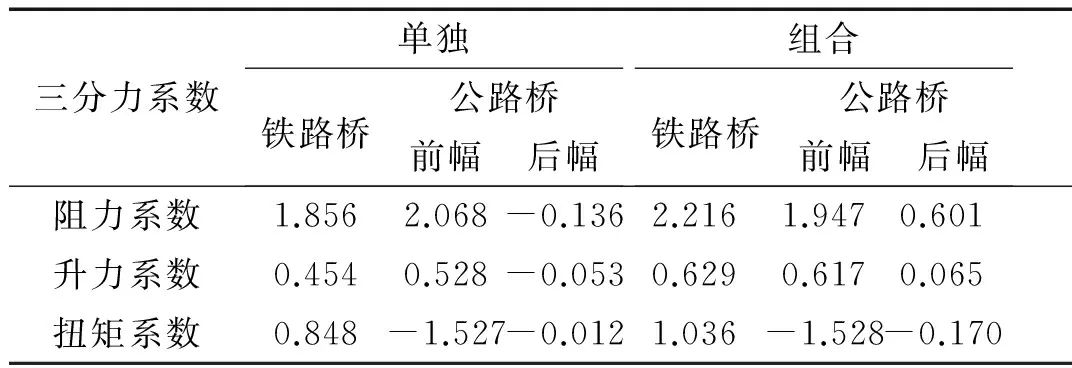
表1　桥梁三分力系数

注：前幅是指迎风侧公路桥幅，后幅是指背风侧公路桥幅。

1.3.4不同间隔高度对列车气动特性的影响

为考查双层桥面不同间隔高度对铁路列车气动特性的影响，分别进行了间隔高度为8.3 m、10.7 m、13.1 m、15.5 m共四种工况的CFD分析，表2给出了不同间隔高度情况下列车的三分力系数，三分力系数随间隔高度的变化如图7所示。

表2　不同间隔高度下列车三分力系数

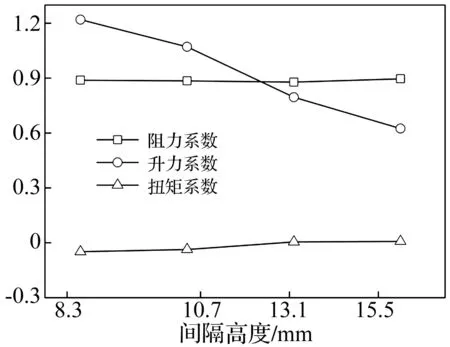
图7　不同间隔高度列车三分力系数的变化曲线Fig.7 Curve of aerodynamic coefficients of train at different height interval cases

从图7可以看出随着间隔高度的增加，列车阻力系数和扭矩系数变化较小，而升力系数却显著降低，这可能是因为随着间隔高度的增加，列车顶部风速降低，由理想伯努利方程可知，列车顶部的动压减小则静压增加，列车底部静压变化很小，故升力有所降低。由此可见公铁两用组合桥上下层桥梁之间的间隔高度对列车升力系数有着重要的影响，间隔高度越小，列车受到的升力系数越大，间隔高度对列车阻力系数和扭矩系数的影响相对较小。

2间隔高度对列车走行性的影响

2.1桥梁有限元模型

因采用分离式设计，公路桥面对铁路桥面力学行为影响较小，故我们针对车辆走行性分析的有限元建模中仅考虑铁路主梁。主梁、桥墩(如图8～9)均采用空间梁单元进行模拟，38孔桥梁有限元模型如图10所示，对该桥动力特性进行分析计算，结构横弯、竖弯见表3。

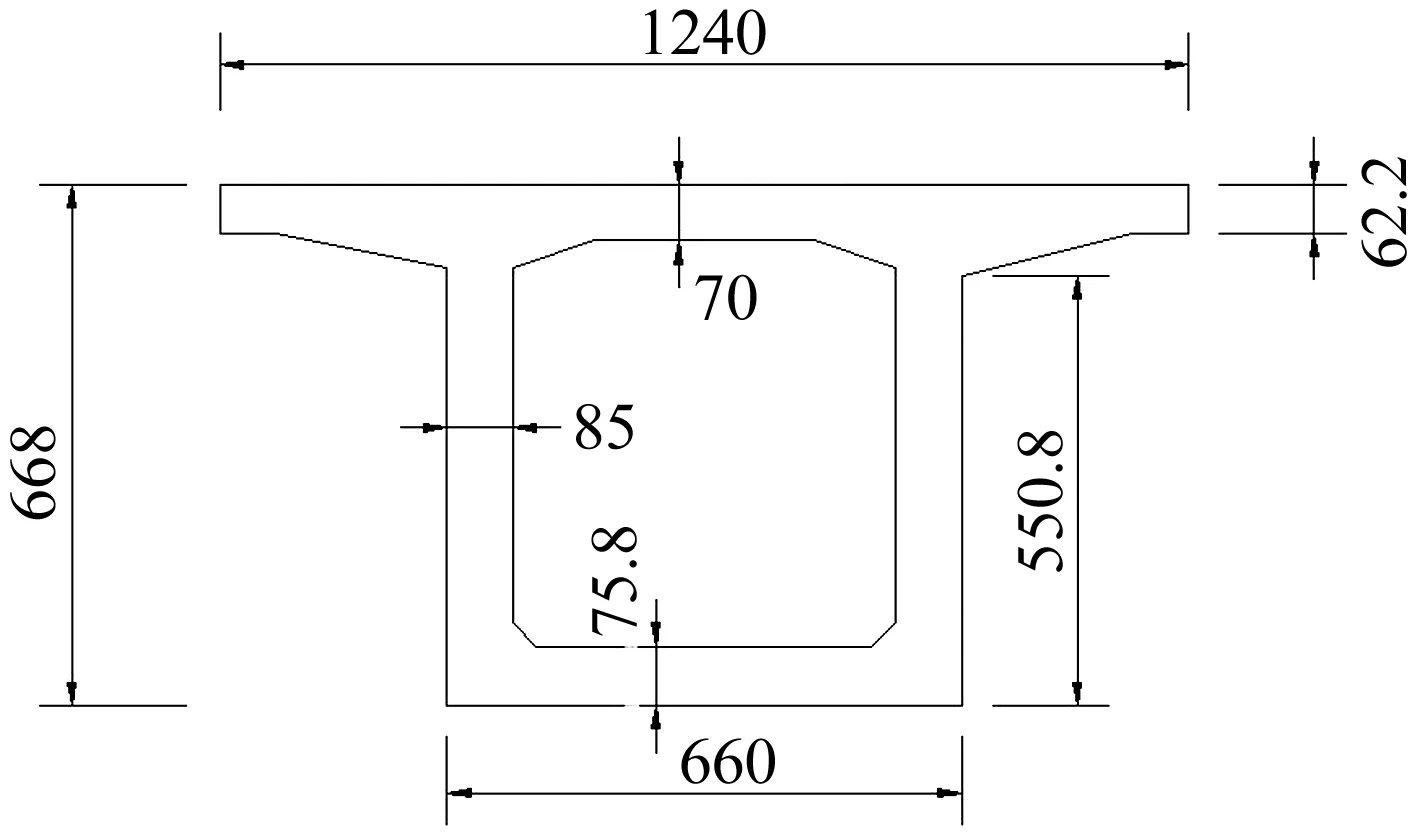
图8　铁路主梁断面(单位：cm)Fig.8 Cross section of railway girder (Unit: cm)

图9　桥墩尺寸(单位：cm)Fig.9 Size of Pier (unit:cm)

图10　桥梁有限元模型Fig.10 Finite element model of bridge

阶次计算频率振型描述11.879主梁纵飘+桥墩顺桥向弯曲23.308主梁一阶对称横弯311.118主梁对称竖弯

2.2风-车-桥耦合振动分析

风-车-桥系统由风-车系统、风-桥系统以及车-桥系统三部分组成。风-车系统中仅考虑风对车辆的定常力和准定常力，忽略自激作用；风-桥系统间的相互作用通过对非线性风荷载的迭代来实现；车-桥系统间的耦合通过车辆、桥梁两子系统间的分离迭代来实现[14]。对于风-车-桥系统，可在满足车辆、桥梁两子系统间的几何、力学耦合关系情况下，采用分离迭代的方法将车辆及桥梁运动方程分别独立求解。侧向风对车辆的行车安全性影响较大[15]，为考查公铁两用桥梁双层桥面不同间隔高度情况下车辆风荷载变化的影响，针对不同工况分别进行了风-车-桥耦合振动分析[16]。

平均风、空间相关的脉动风及随机的轨道不平顺是风-车-桥系统的外在激励源。轨道不平顺谱采用德国低干扰谱，脉动风场模拟采用谱方法[17]，沿主梁等间距模拟了水平脉动风速场和竖向脉动风速场。该桥为跨海桥梁，地表类型取为A类风谱，根据《公路桥梁抗风设计规范》[18]取用。

采用CRH2动力分散式车组进行计算，车速取250 km/h，侧向风平均风速为35m/s，车辆沿迎风侧轨道运行。桥墩和主梁均为混凝土，根据《公路桥梁抗风设计规范》[18]阻尼比取为2.0%。

车辆所受风荷载包括静风力和抖振力，忽略自激力的影响[16]。对于不同间隔高度，静风力和抖振力计算中车辆的三分力系数根据表2取定。

图11和图12给出了双层桥面不同间隔高度情况下35 m/s风速时车辆的响应对比。

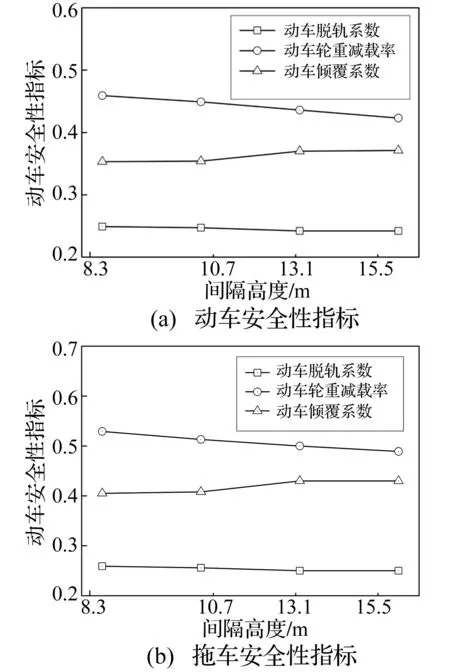
图11　不同间隔高度下车辆安全性指标Fig.11 Vehicle security index at different height interval cases

图12　不同间隔高度下车辆加速度Fig.12 Vehicle acceleration at different height interval cases

从图11、图12中可以看出，间隔高度越大，动车和拖车的竖向加速度和轮重减载率越小，其它响应指标变化较小。随着间隔高度的增加，动车和拖车的轮重减载率下降了约8.5%，动车竖向加速度减小了18.6%，拖车竖向加速度减小了30.4%。间隔高度对列车响应影响明显，设计中应加以考虑。

3结论

本文采用CFD数值模拟和风-车-桥耦合振动分析的方法，分析了分离式公铁两用混凝土箱梁桥公路桥面与铁路桥面间隔高度对列车气动特性和动力响应的影响，得出如下结论：

(1) 分离式公铁两用混凝土箱梁桥主梁较高，横向风作用下双层桥面气动绕流间存在明显的相互干扰现象。单独公路桥或单独铁路桥状态下桥梁的三分力系数与两者组合状态下的三分力系数差异显著。

(2) 对于位于公铁双层桥面之间的铁路列车，间隔高度对车辆风荷载影响较大，随着间隔高度的增加，升力系数显著降低，列车阻力系数和扭矩系数变化相对较小。

(3) 横向风作用下，间隔高度对列车响应的影响明显，间隔高度越大，动车和拖车的竖向加速度和轮重减载率越小，其它响应指标变化相对较小。公铁两用双层桥面间隔高度对列车响应的影响设计中应加以考虑。

参 考 文 献

[1] Ostenfeld K H. Denmarks great belt link[C]//The 1989 ASCE Annual Cicil Engineering Convention, New Or leans：[s.n.],1989.

[2] 杨明智，袁先旭，鲁寨军，等. 强侧风下青藏线列车气动性能风洞试验研究[J]. 实验流体力学. 2008(1):76-79.

YANG Ming-zhi，YUAN Xian-xu，LU Zhai-jun，et al. Experimental study on aero-dynamic characteristics of train running on Qinghai-Tibet railway under cross winds[J].Journal of Experiments in Fluid Mechanic，2008(1):76-79.

[3] 中华人民共和国国家标准. GB 146.2—83标准轨距铁路建筑限界[S].北京：中国标准出版社，1983.

[4] 徐鹤寿，郝有生. 高速铁路建筑限界的研究[J]. 中国铁道科学,1998(4):76-83.

XU He-shou，HAO You-sheng.Study on the structure gauge for high-speed railway[J]. China Railway Science,1998(4):76-83.

[5] 彭月燊. 高速铁路桥梁设计特点[J]. 桥梁建设,1999(3):27-31.

PENG Yue-shen. Design charateristics of high speed railway bridge[J]. Bridge Con-struction,1999(3):27-31.

[6] 李永乐，安伟胜，蔡宪棠，等. 倒梯形板桁主梁CFD简化模型及气动特性研究[J]. 工程力学,2011(增刊1):103-109.LI Yong-le,AN Wei-sheng,CAI Xian-tang,et al. Simplified CFD modal and aerodynamic characteristics of inverted trapezoidal plate-truss deck[J]. Engineering Mechanics,2011(Sup1):103-109.

[7] 李永乐，汪斌，黄林，等. 平板气动力的CFD模拟及参数研究[J]. 工程力学,2009(3):207-211.

LI Yong-le,WANG Bin,HUANG Lin,et al.CFD simulation and parameter study on aerodynamic force of flat plate[J]. Engineering Mechanics,2009(3):207-211.

[8] 许伟. 大气边界层风洞中风场的数值模拟[D]. 哈尔滨:哈尔滨工业大学,2007.

[9] Wilcox D C. Turbulence Modeling for CFD. DCW Industria,Inc.,La Canada,California,1998

[10] 白桦，李加武，胡兆同，等. 近流线型断面静力三分力系数的雷诺数效应识别[J]. 建筑科学与工程学报,2007(4):60-63.

BAI Hua,LI Jia-wu,HU Zhao-tong,et al. Identification of reynolds number effect of tri-component force coeffi-cient of streamline-liked section[J].Journal of Architecture and Civil Engineering,2007(4):60-63.

[11] 张彦.桥梁气动自激力的数值模拟研究[D].成都：西南交通大学，2009.

[12] 李永乐,廖海黎,强士中. 车桥系统气动特性的节段模型风洞试验研究[J]. 铁道学报,2004(3):71-75.

LI Yong-le,LIAO Hai-li,QIANG Shi-zhong. Study on aerodynamic characteristics of the vehicle-bridge system by the section model wind tunnel test[J]. Journal of the China Railway Society,2004(3):71-75.

[13] 汪斌，李永乐，郝超，等. 大跨度连续刚构桥钝化主梁气动特性数值分析[J]. 四川建筑科学研究,2008(5):29-33.

WANG Bin,LI Yong-le,HAO Chao,et al. Numerical simulation of aerodynamic characteristics of the blunt deck of long span continuous rigid frame bridges[J]. Sichuan Building Science Research,2008(5):29-33.

[14] Xia C Y,Lei J Q,Zhang N,et al. Dynamic analysis of a coupled high-speed train and bridge system subjected to collision load[J]. Journal of Sound and Vibration,2012,331(10):2334-2347.

[15] Fujii T,Maeda T,Lshida H,et al. Wind-induced accidents of train/vehicles and their measure in Japan,QR of RTRI,1999(1):50-55.

[16] Li Yong-le,Qiang Shi-zhong,Liao Hai-li,et al. Dynamics of wind-rail vehicle-bridge system[J]. Journal of Wind Engineering and Industrial Aerodynamics,2005,93:483-507.

[17] Li Yong-le,Liao Hai-li,Qiang Shi-zhong. Simplifying the simulation of stochastic wind velocity fields for long cable-stayed bridges[J]. Computers & Structures,2004,82(20):1591-1598.

[18] 中华人民共和国推荐性行业标准. JTG/T D60-01—2004公路桥梁抗风设计规范[S].北京：人民交通出版社，2004.

Aerodynamic interaction between road deck and rail deck of separate-type highway-railway bridges and its effect on train running performance

LI Yong-le1, JIANG Xiao-wei1, SU Yang1, LI Long-an2, LIAO Hai-li1

(1. Department of Bridge Engineering, Southwest Jiaotong University, Chengdu 610031, China；2. China Railway Major Bridge Reconnaissance&Design Institute Co., Ltd., Wuhan 430056, China)

Abstract:There exists aerodynamic interaction between road deck and rail deck of highway-railway bridges under cross wind. In order to investigate the effect of different height intervals between two decks on train running performance, a separate-type highway-railway concrete box girder bridge was taken as an engineering example. The numerical simulation with CFD and the coupled vibration analysis of a wind-vehicle-bridge system were performed to determine train aerodynamic characteristics and to obtain its dynamic response. The results showed that the height interval between two decks has a major influence on train aerodynamic characteristics and its dynamic response; reducing the height interval leads to increase in the train lift coefficient and its vertical acceleration, and the wheel load reduction ratio increases as well; the effect of height intervals between two decks should receive more attention when selecting the optimal height interval in the design of highway-railway bridges.

Key words:highway-railway bridges; height interval; wind-vehicle-bridge system; running performance; CFD

基金项目：国家自然科学基金项目(U1334201;51278434)；国家科技支撑计划课题(2012BAG05B02)；四川省青年科技创新研究团队项目(15CXTD0005)

收稿日期：2015-02-02修改稿收到日期：2015-04-14

中图分类号:U24

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.012

第一作者 李永乐 男，博士，教授，博士生导师，1972年生