基于结构加速度误差最小化的声学预测模型修正

徐中明 ， 何治桥 ， 贺岩松 ， 张志飞 ， 夏小均

(1.重庆大学 机械传动国家重点实验室，重庆　400030； 2. 重庆大学 汽车工程学院，重庆　400030)

基于结构加速度误差最小化的声学预测模型修正

徐中明1，2， 何治桥2， 贺岩松1，2， 张志飞1，2， 夏小均2

(1.重庆大学 机械传动国家重点实验室，重庆400030； 2. 重庆大学 汽车工程学院，重庆400030)

摘要：针对FEA(有限元分析)声学预测方法，提出了基于结构加速度响应误差最小化的声学预测模型修正方法。以模态迭加法为基础，结合模态应变能模态阻尼识别和频域载荷识别原理，重构了FEA声学预测模型，通过遗传算法优化结构损耗因子，使结构加速度响应计算值与实验值误差最小化，从而识别系统模态阻尼比及激励力，实现对声学预测模型参数的修正。将该方法与传统计算方法预测结果对比，结果表明：该方法可以精确识别系统模态阻尼和激励力，提高模型预测精度。

关键词：FEA；声学预测；加速度误差；遗传算法

由复杂弹性封闭空腔结构在动态载荷激励下振动而形成的空间内部声场是工程实际中最具代表性的一类声场，实现对这类声场的声学响应预测和分析具有重要的工程应用价值[1]。目前，声学预测方法主要分为有限元法、边界元法以及统计能量法。其中有限元、边界元方法适用于结构模态密度小于5的低频声学预测，统计能量法对于高频预测具有较好的精度，而中频声学预测则常采用有限元和统计能量混合建模方法。马天飞等[2]建立某驾驶室声固耦合有限元模型，对不同工况下的车内噪声频率响应进行分析，对比仿真结果和实验结果发现：模型结构阻尼和声学阻尼参数的偏差将导致仿真结果与实验结果存在较大差异，同时，空气传播噪声和背景噪声也是导致差异的主要因素；张志勇等[3]通过试验测试实车匀速工况下驾驶室4个悬置附近加速度信号，将其作为预测模型外部激励输入，基于耦合有限元法对驾驶员耳旁噪声进行了预测，通过与试验测试值对比，验证了所建立的驾驶室声固耦合模型具有一定的预测精度。然而在实际运用中，仿真结果和试验值之间仍然存在较大偏差，预测模型的精度有待进一步提升。因此，利用试验数据修正模型以得到更精确的预测模型正逐渐成为该领域研究的热点。张宝强等[4]提出一种同时使用模态频率和有效模态质量作为目标量的残差进行结构动力学有限元模型修正的新方法，采用仿真算例验证了所提出方法的正确性和有效性；魏锦辉等[5]以各阶模态柔度矩阵中各元素相对变化作为指标，提出了基于模态柔度灵敏度解析表达式的有限元模型修正方法。

因激励力信号测试困难，在目前的声学预测计算中，一般采集激励点附近加速度信号，然后将加速度信号转换为力信号，作为激励加载到有限元模型。转换方法主要分为大质量法和约束模态法。大质量法在模型激励点加载一个质量较大的质量点，通过与加速度相乘得到激励力载荷；约束模态法则基于约束模态计算激励点频率响应约束反力，进而将约束反力加载到模型计算动态响应。对于模态阻尼比的设置，则根据经验，采取设置全局均匀模态阻尼比的方法。这些简化处理方法导致有限元模型参数与实际系统的差异增大，制约着模型预测精度的提升。

本文提出一种基于结构加速度误差最小化的有限元声学预测模型修正方法。结合模态应变能模态阻尼

识别和频域载荷识别原理，通过遗传算法优化模型结构损耗因子，使所计算的结构加速度值与实验值的差异最小化，识别系统模态阻尼比和载荷参数，构建新的建模流程。通过与传统方法对比，结果表明：该方法可以通过精确识别模态阻尼比和荷载参数有效提升模型预测精度。

1基本理论

1.1模态阻尼识别

模态阻尼识别方法主要分为试验方法和数值分析方法。常用的试验方法包括半功率带宽法、半功率带宽改进法、基于内积模极值诊断法等[6]。在新产品开发阶段，往往需要借助数值计算方法，模态应变能法是最常用的数值计算方法。

各阶模态阻尼比可以通过相应的模态应变能以及结构损耗因子进行识别。第r阶模态阻尼比可表示为[7]

(1)

式中：ESEr,n为第n组单元的第r阶模态应变能；ηstruct为第n组单元结构损耗因子；ESEr,tot为所有单元第r阶模态应变能之和；ζr,ηr为第r阶模态阻尼比和模态损耗因子。

由于结构损耗因子受材料、结构形状等因素影响，对于不同材料和形状的结构，其结构损耗因子差别可能很大，因此，需要根据实际情况，将单元分为多组，分别定义各组的结构损耗因子。结构损耗因子随频率变化，当分析频带较窄时，在该分析频带内可近似为一常数。

1.2载荷识别

对于系统动力学微分方程的求解，外界激励为力输入，但采用直接方法获取结构激励力在实际操作中会遇到很多问题[8]。为了精确获得结构工作激励力，通常不是直接测量，而是采用间接方法计算得到。

载荷识别技术是在已知结构系统参数的情况下，基于外界输入载荷下的动态响应来反求作用于系统的动态荷载。频域法主要利用动态载荷和响应之间的频响函数的求逆实现，频响函数的性态直接影响动载荷识别的结果[9]。

对于线性系统，当存在激励力F1,F2…Fn时，系统各点存在响应Y1,Y2…Ym，令点n至点m的频响函数为Hmn，则由系统运动方程可得：

(2)

进一步可得激励力矩阵表达式：

(3)

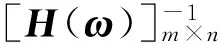
由式(3)可知，通过各加速度测点响应值与频响函数逆矩阵，可以计算出各激励点的工作激励力。该方法考虑了各路径之间的交叉耦合现象，计算出的激励力具有较高精度[10]。同时，为了抑制噪声，避免数值问题，使计算的激励力更加精确，应使响应点数目m不小于激励点数目n，即m≥n。

2模型修正

2.1理论推导

在模态空间中，根据系统动力学方程可推导出激励点l至响应点p的频响函数表达式[11]为：

(4)

其中：

(5)

式中：φlr表示测点l第r阶模态振型系数；φpr表示测点p第r阶模态振型系数。Cr为第r阶模态阻尼，Mr为第r阶模态质量，ωr为第r阶模态频率。

将式(3)中物理坐标下的传递函数矩阵替换为模态空间中的传递函数矩阵可得：

(6)

经模态坐标变换可得系统响应为：

(7)

式中：X(ω)为频率为ω时系统的位移响应向量；Φ为模态矩阵，其中每一列表示某阶模态的振型向量，由各位置的模态振型系数构成；Q表示模态坐标向量，其元素代表各阶模态贡献量； Km为模态刚度矩阵，Mm为模态质量矩阵Cm为模态阻尼矩阵，

将式(4)、(5)代入式(7)，则结构动态响应可表示为：

X(ω)=fs(ω,ωr,Φ,Km,Mm,

ESE,ηstruct,{Y(ω)})

(8)

对于结构传播噪声，内部声场由边界条件和介质属性决定，边界条件包括结构振动边界条件和声阻抗边界条件[12]。当介质属性和阻抗边界条件不变时，声腔声学响应仅受结构振动边界条件影响。因此，提高模型声学预测精度可以通过提升结构模型的精度来实现。

参数ω,ωr,Φ,Km,Mm,ESE的准确程度依赖于有限元前处理过程，且不易更改。因此，在模型前处理满足要求并不再变更的前提下，基于模态迭加法的系统响应仅受结构损耗因子影响。

设用于载荷识别的加速度测点集为A，待计算的响应点集为B。

当B⊂A时，忽略ω,ωr,Φ,Km,Mm,ESE与系统真实值的误差，则不论ηstruct是否等于真实值，式(8)为一恒等式。

当B⊄A时，由于ηstruct与真实值均存在差异，从而导致点集B响应计算值与实际值之间的误差。

在参数ω,ωr,Φ,Km,Mm,ESE,{Y(ω)}确定的条件下，对于任意的ηstruct，都存在唯一的响应X(ω)与之对应，因此通过优化结构损耗因子，使点集B(B⊄A)加速度响应计算值逐步逼近实测值，反向识别系统的模态阻尼以及激励力，进而将识别的参数加载于声学预测模型计算声学响应，提升模型预测精度。

2.2建模流程

基于上述理论，对现有FEA声学预测建模方法进行改进，提出基于结构加速度误差最小化的模型修正方法，具体建模流程如图1所示。

(1) 建立结构有限元模型以及声腔有限元或边界元模型，并求解结构模态。实验测试点集A和点集B加速度频谱信号。

(2) 初始化结构损耗因子，结合模态应变能识别各阶模态阻尼比。基于求解和识别的模态参数采用模态迭加法分别求解各激励点至测点集A中各点频响函数，结合实测加速度频谱信号识别激励力参数。

(3) 基于识别的激励力以及模态参数计算测点集B中各点加速度响应，求得计算值与实测值误差。以结构损耗因子为变量，计算值与实测值误差最小化为目标进行优化计算，直至收敛。

(4) 使用经过优化识别的模态阻尼比、激励力以及结构模态参数，结合声腔模型和阻抗边界条件计算声腔声学响应。

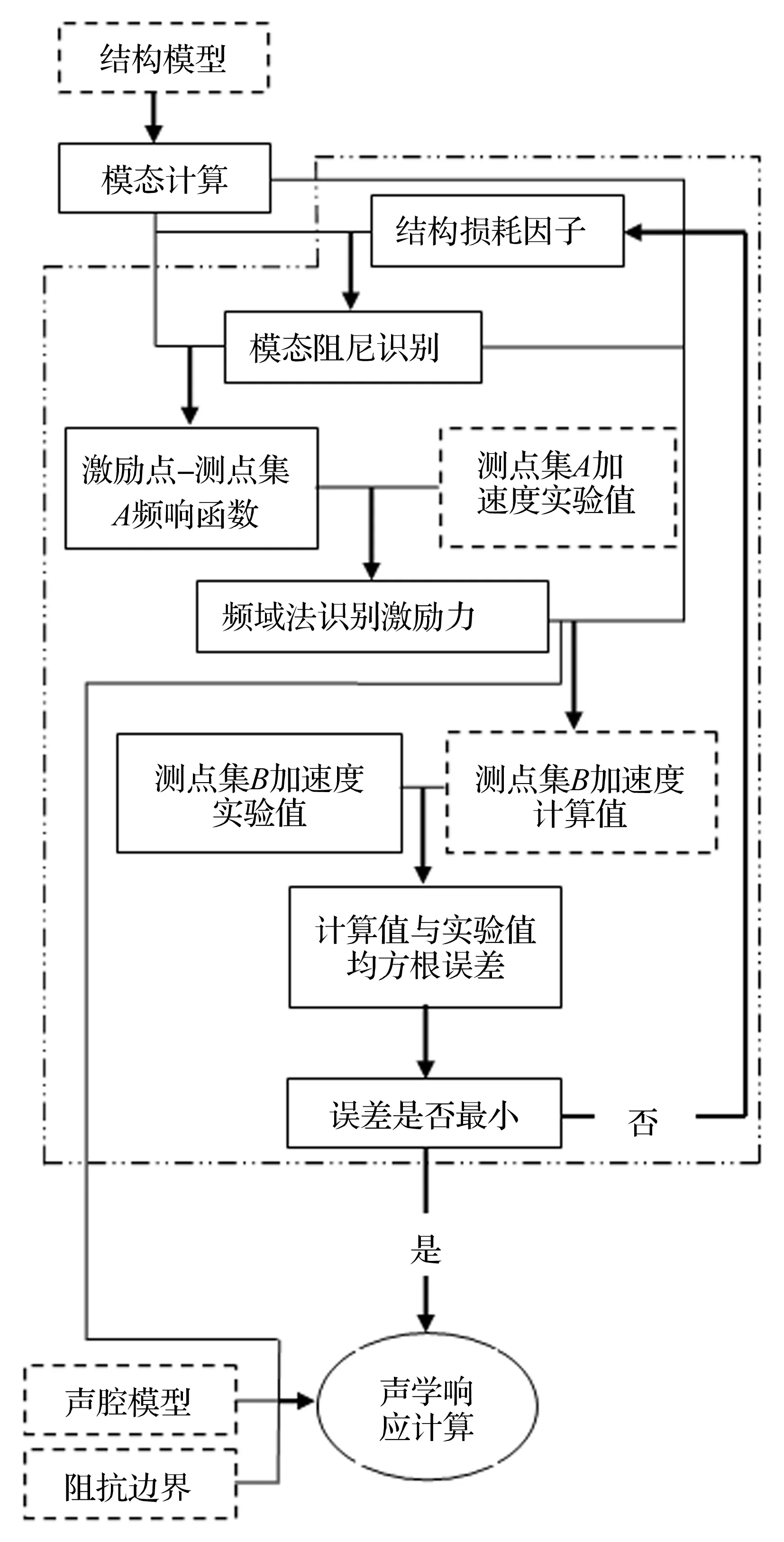
图1　建模流程图 Fig.1 The flow chart of modeling

3算例验证

为验证上述方法的有效性，利用简化模型，分别使用传统计算方法和本文提出的方法计算声腔中同一场点声压响应，并与该位置模拟的实际响应进行对比。

简化模型为一长宽高均为500 mm的立方体结构，厚度为2 mm，密度为7 800 kg/m3，弹性模量为207 000 MPa，泊松比为0.3。在该立方体的a,b,c面各选取一点加载垂直于相应面的20～400 Hz力激励，激励力参数和模态阻尼比为自定义，激励力频谱如图3所示。设置的各阶模态阻尼比如图4所示。在Virtual.lab中采用声振耦合方法计算封闭空间中一特定场点声压响应，作为该场点在该工况下的实际响应值。各点位置见图2。

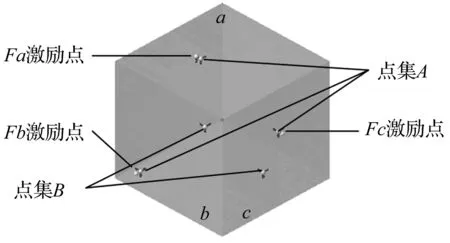
图2　激励点和测点位置图Fig.2 Thelocations of incentive and measuring points

3.1传统方法声学预测

在模型的三个激励点附近各设置一个加速度采集点，构成点集A，计算输出各点三向加速度响应频谱，用以模拟试验采集的结构加速度响应信号。将计算输出的三向加速度频谱信号作为激励信号加载于模型实际激励点，并设置全局均匀模态阻尼系数为实际各阶模态阻尼比的平均值，约为7%，采用声振耦合方法计算得到声腔内同一场点声压响应。

3.2加速度误差最小化方法声学预测

各参数设置如下：

(1) 变量：简化模型由六个板件构成，针对每个板件分别设置结构损耗因子，构成系统6个输入变量，即：

η1,η2,η3,η4,η5,η6

(2) 约束：结合实际情况，设置变量约束条件为：

0.01≤ηi≤0.5(i=1,2,3,4,5,6)

(9)

(3) 目标：以响应点集B的加速度计算值与实际值均方误差最小化为优化目标，可表示为：

min:

(10)

式中：g为目标函数值；ω为频率；Accir(ω)为加速度响应点集B中第i点加速度实测值；Accim(ω)为加速度响应点集B中第i点加速度计算值。n为加速度响应点集B中响应点个数，这里n=2 。

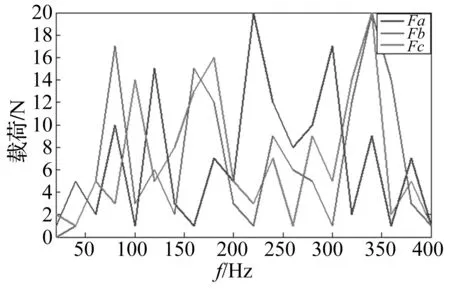
图3　实际激励力频谱Fig.3 The actual spectrum of exciting forces

(4) 优化算法：遗传算法。遗传算法是启发式的搜索方式，得出的最优解与实际最优解的误差较小[13]。设置种群数量为20，进化次数为200次，选择概率为0.8，交叉概率为0.5，变异概率为0.1，优化经过115次迭代收敛。目标函数进化曲线如图5所示。经过优化，识别的模态阻尼比与实际模态阻尼比对见图6；识别的激励力与实际激励力对比如图7所示。

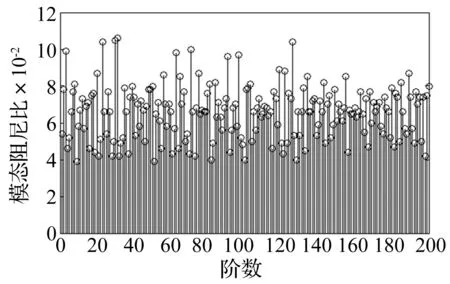
图4　实际模态阻尼比Fig.4 The actual modal damping ratio

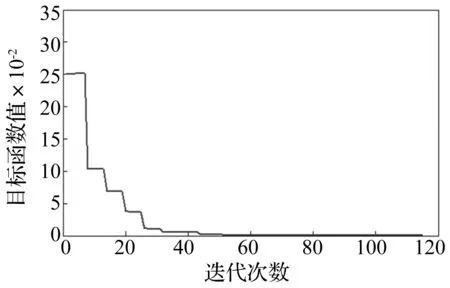
图5　目标函数值进化曲线图Fig.5 The evolution curve of objective function value

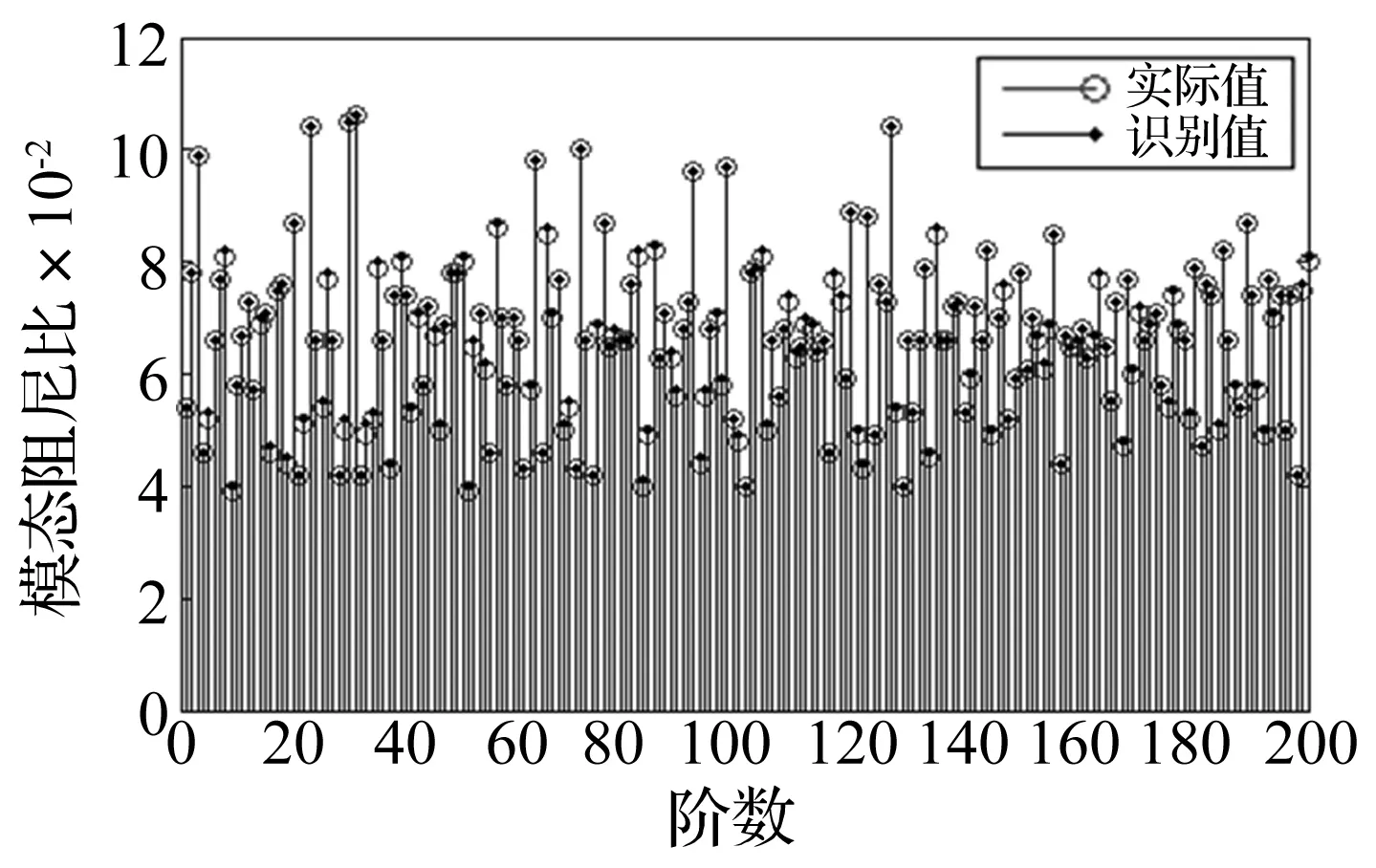
图6　优化后模态阻尼比与实际值对比图Fig.6 The Contrast diagram of modal damping ratio

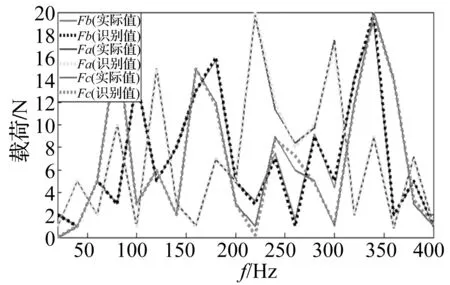
图7　优化后识别的激励力与实际激励力对比图Fig.7 The Contrast diagram of exciting forces

3.3结果对比

由表1和图8对比结果可以看出：采用本文提出的模型修正方法，模态阻尼比均方根误差(RMSE)减小到6.49×10-4，百分比误差为0.6%；在此基础上，通过计算激励点到响应点频响函数，采用频域法识别出的载荷均方根误差和百分比误差分别为0.53 N和2.52%；将识别的模态阻尼比和激励力加载于声学预测模型，场点声压响应均方根误差仅为0.98 dB，误差百分比从7.31%减小到0.69%。相对于传统计算方法，模型精度有了明显提高。

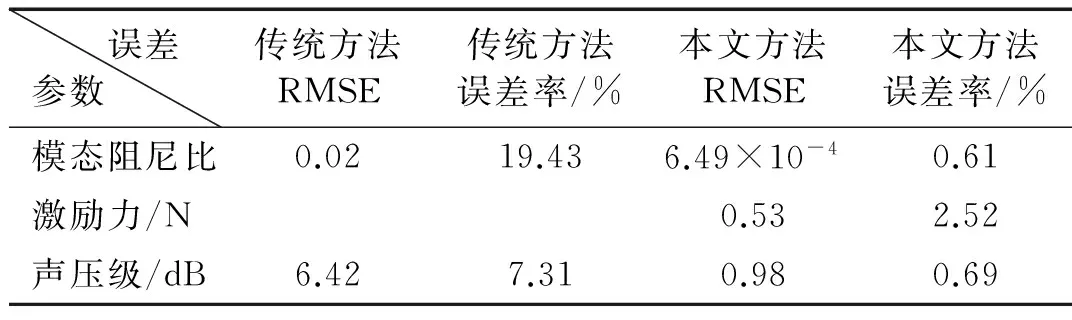
表1　各参数优化前后预测误差对比

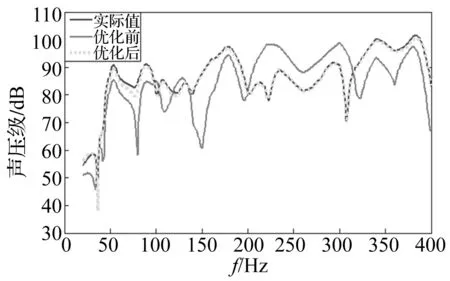
图8　优化前后声压响应频谱与实际频谱对比图Fig.8 The Contrast diagram of SPL response spectrum

4结论

基于模态阻尼识别和载荷识别理论，提出了以结构加速度误差最小化为目标的的FEA声学预测模型修正方法，通过遗传算法优化结构损耗因子，使结构加速度响应计算值与实验值差异最小化，识别系统模态阻尼比和激励力，提升预测模型精度。通过与传统计算方法对比，证明了该方法预测精度高于传统方法。

参 考 文 献

[1] 肖悦，陈剑，胡定玉，等. 复杂封闭声场面板声学贡献度识别的等效源法[J]. 声学学报，2014，39(4)：489-500.

XIAO Yue,CHEN Jian,HU Ding-yu,et al. Equivalent source method for identification of panel acoustic contribution in irregular enclosed sound field[J]. Acta Acustica，2014，39(4)：489-500.

[2] 马天飞，高刚，王登峰，等. 基于声固耦合模型的车内低频结构噪声响应分析[J]. 机械工程学报，2011,47(15)：76-82.

MA Tian-fei,GAO Gang,WANG Deng-feng,et al. Response analysis of interior structure noise in lower frequency based on structure-acoustic coupling model[J]. Journal of Mechanical Engineering,2011,47(15)：76-82.

[3] 张志勇，张义波，刘鑫，等. 重型卡车驾驶室结构噪声预测与板件声学贡献度分析[J]. 振动与冲击,2014,33(13):67-71.

ZHANG Zhi-yong,ZHANG Yi-bo,LIU Xin,et al.Structure-borne noise prediction and panel acoustic contribution analysis of a heavy-duty truck cab[J]. Journal of Vibration and Shock,2014,33(13):67-71.

[4] 张宝强，陈国平，郭勤涛. 基于模态频率和有效模态质量的有限元模型修正[J]. 振动与冲击，2012,31(24)：69-73.

ZHANG Bao-qiang,CHEN Guo-ping,GUO Qin-tao. Finiteelement model updating based on modal frequency and effective modal mass[J]. Journal of Vibration and Shock,2012,31(24)：69-73.

[5] 魏锦辉，任伟新，万华平. 基于模态柔度的有限元模型修正方法[J]. 振动与冲击，2013,32(13)：106-111.

WEI Jin-hui,REN Wei-xin,WAN Hua-ping.Finite element model updating method based on modal flexibility[J]. Journal of Vibration and Shock,2013,32(13)：106-111.

[6] 赵晓丹,张中业,骆英.基于内积运算与迭代算法的密集模态阻尼识别[J]. 农业机械学报,2011,42(4):206-210.

ZHAO Xiao-dan,ZHANG Zhong-ye,LUO Ying. Damping identification for closely spaced modes based on inner product caculation and iterative algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery,2011,42(4):206-210.

[7] Montalvão D,Silva J M M. An alternative method to the identification of the modal damping factor based on the dissipated energy[J]. Mechanical Systems and Signal Processing,2015,54(55):108-123.

[8] Wang Bin-xing,Zheng Si-fa,Zhou Lin,et al. Acoustic modelling and analysis of vehicle interior noise based on numerical calculation[C]//International Conference on Intelligent Computation Technology and Automation,2010:404-407.

[9] 肖悦. 基于面板声学贡献度的封闭空腔结构内声场分析的若干关键问题研究[D]. 合肥：合肥工业大学，2014.

[10] 唐荣江. 车内声品质评价预测与控制技术研究[D]. 长春：吉林大学，2013.

[11] 傅志方，华宏星. 模态分析理论与应用[M].上海;上海交通大学出版社，2000.

[12] 杜功焕，朱哲民，龚秀芬. 声学基础[M]. 南京：南京大学出版社，2001.

[13] 雷伟军，程筱胜，戴宁，等. 基于改进遗传算法的多模型加工路径规划[J]. 机械工程学报，2014,50(11)：153-161.

LEI Wei-jun,CHENG Xiao-sheng,DAI Ning,et al. Multi-model machining path planning based on improved genetic algorithm[J]. Journal of Mechanical Engineering,2014,50(11)：153-161.

Modified model for acoustic prediction based on structural acceleration error minimization

XU Zhong-ming1,2, HE Zhi-qiao2, HE Yan-song1,2, ZHANG Zhi-fei1,2, XIA Xiao-jun2

(1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400030, China;2. College of Vehicle Engineering, Chongqing University, Chongqing 400030, China)

Abstract:A model modifying method for finite element analysis (FEA) acoustic prediction based on the minimization of structural acceleration response error was presented. The FEA acoustic prediction model was reconstructed in combination with modal damping identification, load identification in frequency domain and the modal superposition method. The error between calculated values and test values of structural acceleration response was minimized by optimizing structural loss factors with the genetic algorithm (GA).Then, the accurate modal damping ratios and exciting forces were identified to optimize parameters of the acoustic prediction model. The comparison between prediction results of the traditional method and the proposed method showed that the proposed method can improve the model prediction precision by accurately identifying a system’s modal damping ratios and exciting forces.

Key words:FEA; acoustic prediction; acceleration error; genetic algorithm

基金项目：中央高校基本科研业务费科研专项(CDJZR14115501)；重庆市研究生科研创新项目(CYB14036)

收稿日期：2015-04-02修改稿收到日期：2015-05-18

中图分类号:TH212；TH213.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.006

第一作者 徐中明 男，教授，博士生导师，1963年生