横纵激励下几何非线性复合材料层合梁的混沌同步

王龙飞 ， 韩志军 ， 闫晓鹏 ， 路国运

(1.太原理工大学 力学学院，太原　030024； 2.太原理工大学 建筑与土木工程学院，太原　030024)

横纵激励下几何非线性复合材料层合梁的混沌同步

王龙飞1， 韩志军1， 闫晓鹏1， 路国运2

(1.太原理工大学 力学学院，太原030024； 2.太原理工大学 建筑与土木工程学院，太原030024)

摘要：基于里兹-伽辽金法，将考虑几何非线性的一端固支一端夹支复合材料层合梁的控制方程简化为典型的Duffing方程；引入了Duffing-Van Der Pol系统，通过两种系统的分岔图说明了它们共同达到混沌时的参数值；通过广义投影同步法，实现了Duffing系统和Duffing-Van Der Pol系统的精确同步，得到了实现两种系统同步的控制器；分别将两种系统通过Matlab进行了数值仿真，得到了两种系统的同步误差曲线图、二维相图和三维相图，从而验证了混沌同步的准确性。

关键词：复合材料；混沌同步；DVP系统；广义投影同步

混沌运动研究是近20年发展起来的关于非线性动力学系统中一种特殊运动方式的研究，它起源于人类对大自然的不断探索，其同步被广泛的应用于各种工程技术方面，尤其在保密通讯中的应用令人瞩目，由此引申出了三大技术：混沌遮掩、混沌调制和混沌开关技术。此外，混沌在超宽带通信和数字水印等方面的应用也在最近几年飞速发展。因此，关于混沌同步的研究有重大的意义和实际价值，被越来越多的学者所关注[1-3]。

混沌同步最早是由美国海军实验室的Pecora等[4]提出的，他们在电路实验中首次实现了混沌的同步，其后，关于混沌同步的研究也越来越热门；Kocarev等[5]提出了一种新的APD分解法，改进了之前的PC同步法，并将其应用到了通信工程中；Pyragas[6]基于反馈调节的思想，提出了一种变量反馈同步法，该方法因为不改变原系统的混沌特性而被广泛应用于电路、激光和振荡器等系统之间的同步；Mainieri等[7]提出了投影同步法，将对应状态的振幅按照一个比例因子进行演化，且得到了广泛应用；基于此，Yan等[8]提出了广义投影同步，可以使所有响应系统和驱动系统的对应状态变量都满足比例关系且相空间可以自由拉伸或压缩；Hu等[9]提出了一种更一般的方法，这种方法不局限于状态变量满足相同的比例关系，称之为全状态混合投影同步；闵富红等[10-11]分别研究了两个相同的四维混沌系统的同结构广义投影同步以及Lorenz系统和Chen系统的改进自适应广义投影同步；王宇野等[12]研究了异结构的不确定混沌系统的广义投影同步，并以Rössler系统和Lü系统的同步为例说明了异结构同步的问题；冯浩等[13]研究了Chen系统和Liu系统的广义投影同步，并将其应用在电路设计方面。以上研究分别利用了不同的方法实现了不同系统之间的混沌同步，然而关于复合材料层合梁在横纵外载激励下的新型混沌同步方法的研究，却鲜有文献提及。

基于此，本文考虑系统的几何非线性，应用广义投影同步法，研究复合材料层合梁在发生非线性振动时的混沌同步，从而通过适当的控制器，将其精确同

步为Duffing-Van Der Pol系统，并广泛应用于力学与工程、激光物理、化学以及生命科学中。

1系统的控制方程

图1是一端固支一端夹支的复合材料层合梁，杆长为L，横截面A=bh，轴向压力为P1=F0，横向扰动力为P2=Fcosωt。若不考虑轴向惯性，由Hamilton原理可导出复合材料层合梁的振动方程，如下：

(1)

(2)

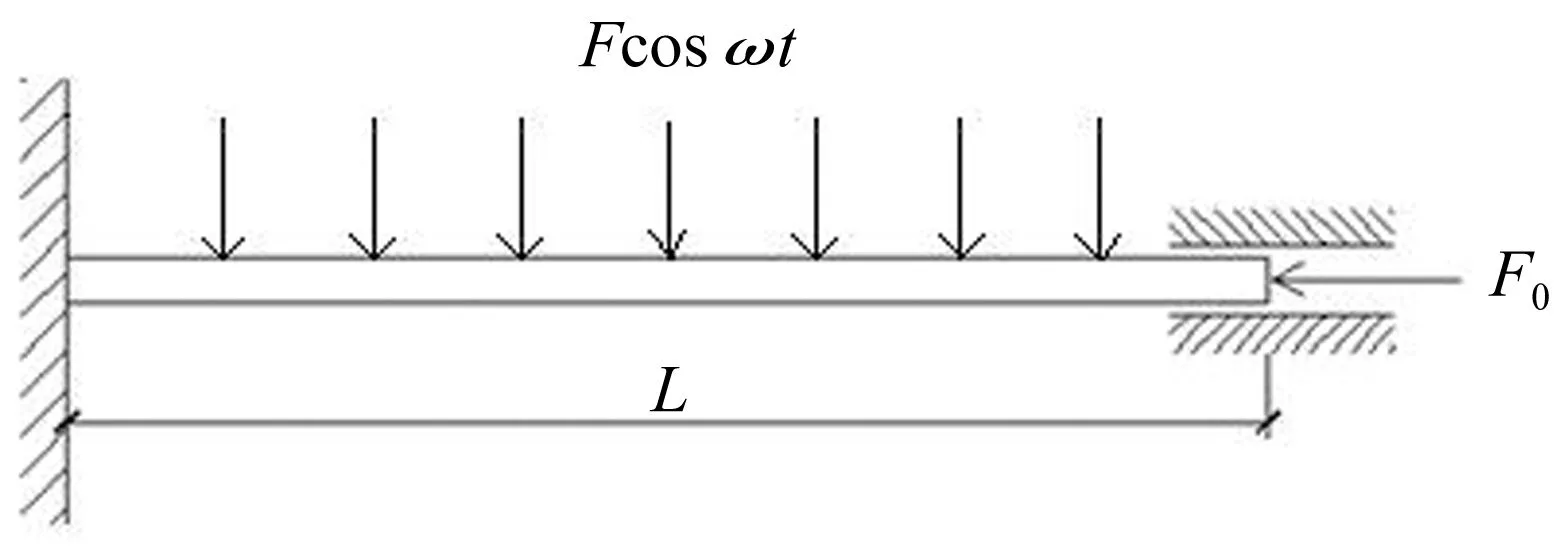
图1　一端固支一端夹支下梁的受载示意图Fig.1 Theclamped-fixed bar by the load

整理式(1)和式(2)，得到由横向位移表达的控制方程为：

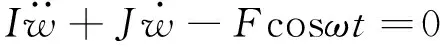
(3)

令：

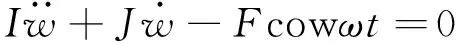
(4)

取满足一端固支一端夹支的边界条件，即：w(0,t)=w(L,t)=w′(0,t)=w′(L,t)=0，由此可得到位移模态为：

(5)

根据里兹-伽辽金法，通过变分和分步积分，式(4)可化简为：

(6)

式(6)可写成如下Duffing方程的形式：

(7)

式(7)是复合材料层合梁控制方程的Duffing方程系统，因为两者都是同一振动系统，所以可以进行等价替代。

2Duffing系统和DVP系统的混沌同步

DVP系统(Duffing-Van Der Pol,DVP)是Duffing系统和Van Der Pol振荡系统的结合，它既具备了Duffing系统的非线性项、具有一定的恢复力，又兼备了Van-Der Pol振荡系统非线性阻尼项，有一定的维持自激振动的能力，可以用来模拟人心脏的振动以及含有负阻原件的电路等，受迫DVP系统可以表示为下式：

(8)

利用广义投影同步法[14]，可以将DVP系统作为驱动系统，Duffing系统作为响应系统，于是这两个系统可以分别表示为：

驱动系统：

(9)

响应系统：

(10)

考察μ、ω和f的取值，要满足Duffing系统和DVP系统能同时进入混沌，进而方便讨论它们在发生混沌下的同步，下面先讨论两种系统随着分岔参数f变化的系统分岔图，然后给出两系统同时发生混沌的参数值，令μ=0.2，ω=1，可得图2分岔图。

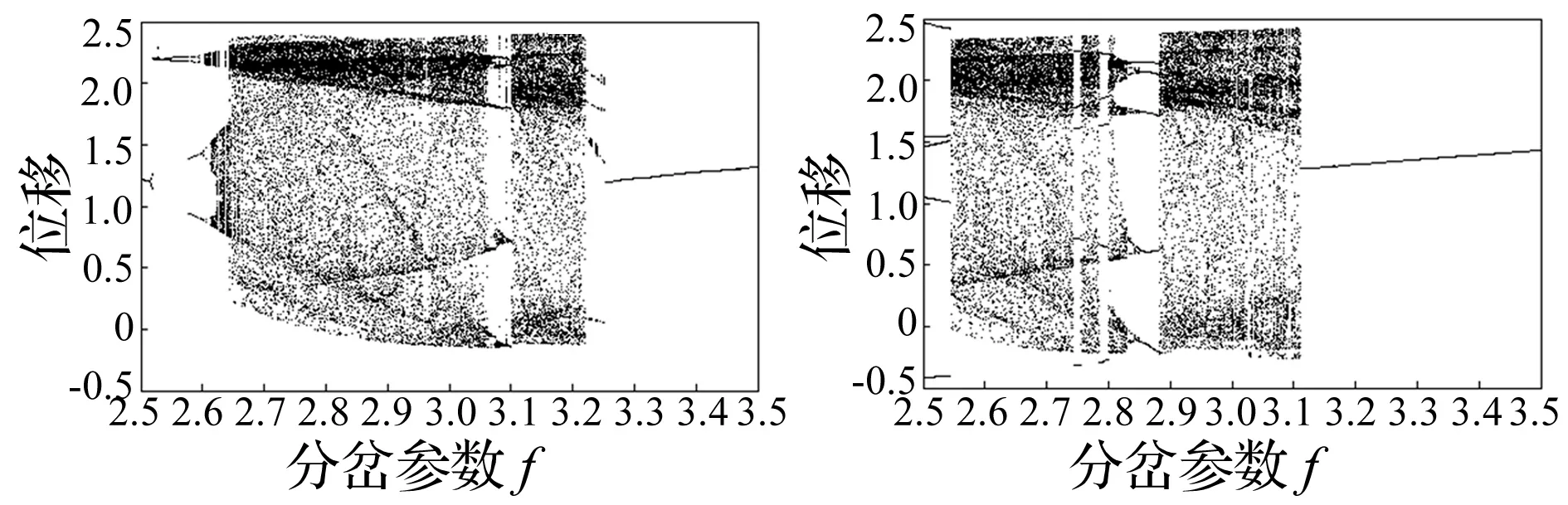
图2　系统随f变化的分岔图(左为Duffing，右为DVP)Fig.2 Bifurcation diagrams with the change ofparameters f (Duffing in the left, DVP in the right)

图2表明：当f=3时，无论是Duffing系统还是DVP系统都已进入了混沌状态，因而可取μ=0.2，ω=1，f=3进行分析讨论。

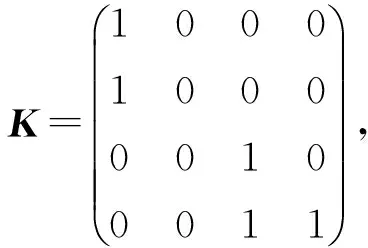
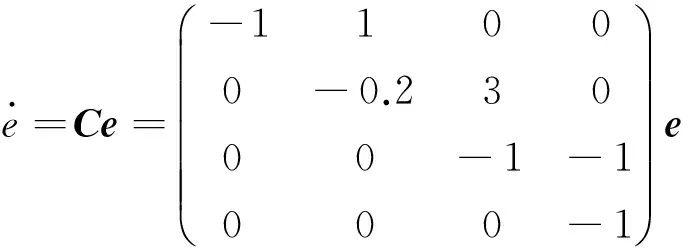
(11)

u1=(κ1-κ2)x2-e1

(12a)

0.4κ2x2+3(κ2-κ3)x3-e1

(12b)

u3=(κ4-κ3)x4-e3

(12c)

u4=(κ4-κ3)x3-e3-e4

(12d)

可用Matlab模拟给出式(9)和(10)的异结构混沌同步过程。

3数值仿真和讨论

取两个系统的初值如下：

(13)

本文研究两个异结构之间的精确同步，取缩放系数都为1，在同步控制器u的作用下，可以得到图3两个四维映射系统间的同步误差曲线图。

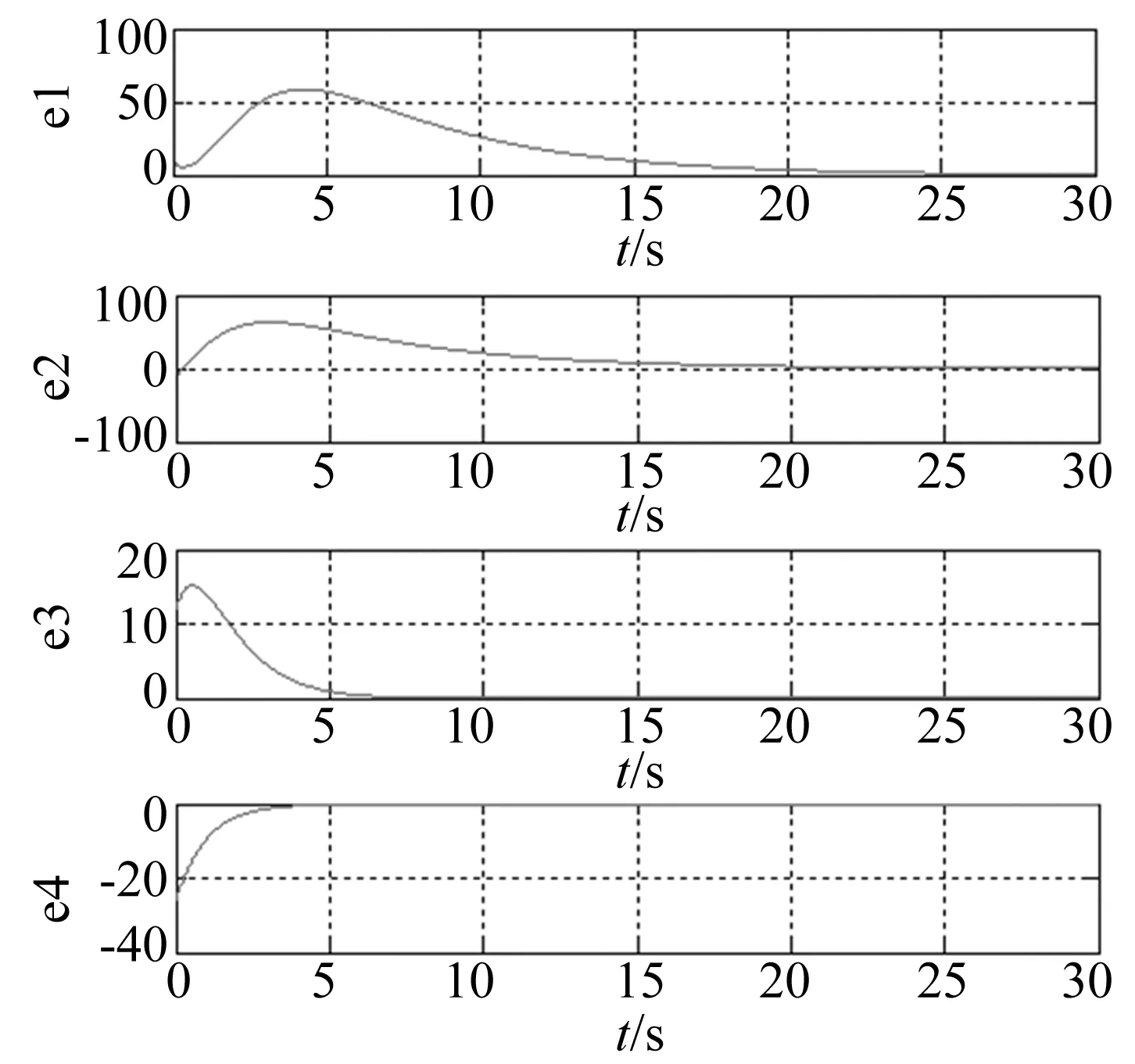
图3　两系统间的同步误差曲线图Fig.3 Synchronous error curve diagrams of two systems

图4是同步前Duffing系统和DVP系统的二维相图，图5是同步前Duffing系统和DVP系统的三维相图，可以看出DVP系统的二维相图类似于“蚕豆”型，而Duffing系统的二维相图为“倒八”型，两者有明显的区别。图4和图5共同表明：Duffing系统和DVP系统在达到混沌时，相轨迹图均杂乱无序，但两者之间有一定的区别，这与DVP系统本身的非线性阻尼项有关。在经过控制器作用，响应系统与驱动系统达到精确同步后，可以得到图6。

此外，还可以通过平面相图或空间相图来形象的说明Duffing系统和DVP系统之间的混沌同步过程。

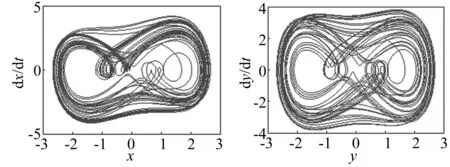
图4　同步前两系统的二维相图(左为DVP，右为Duffing)Fig.4 2D-phase-trajectory diagrams of two systems before synchronization(DVP in the left, Duffing in the right)

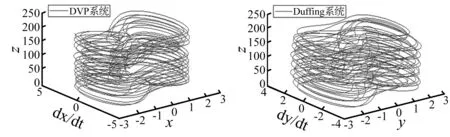
图5　同步前两系统的三维相图(左为DVP，右为Duffing)Fig.5 3D-phase-trajectory diagrams of two systems before synchronization(DVP in the left, Duffing in the right)

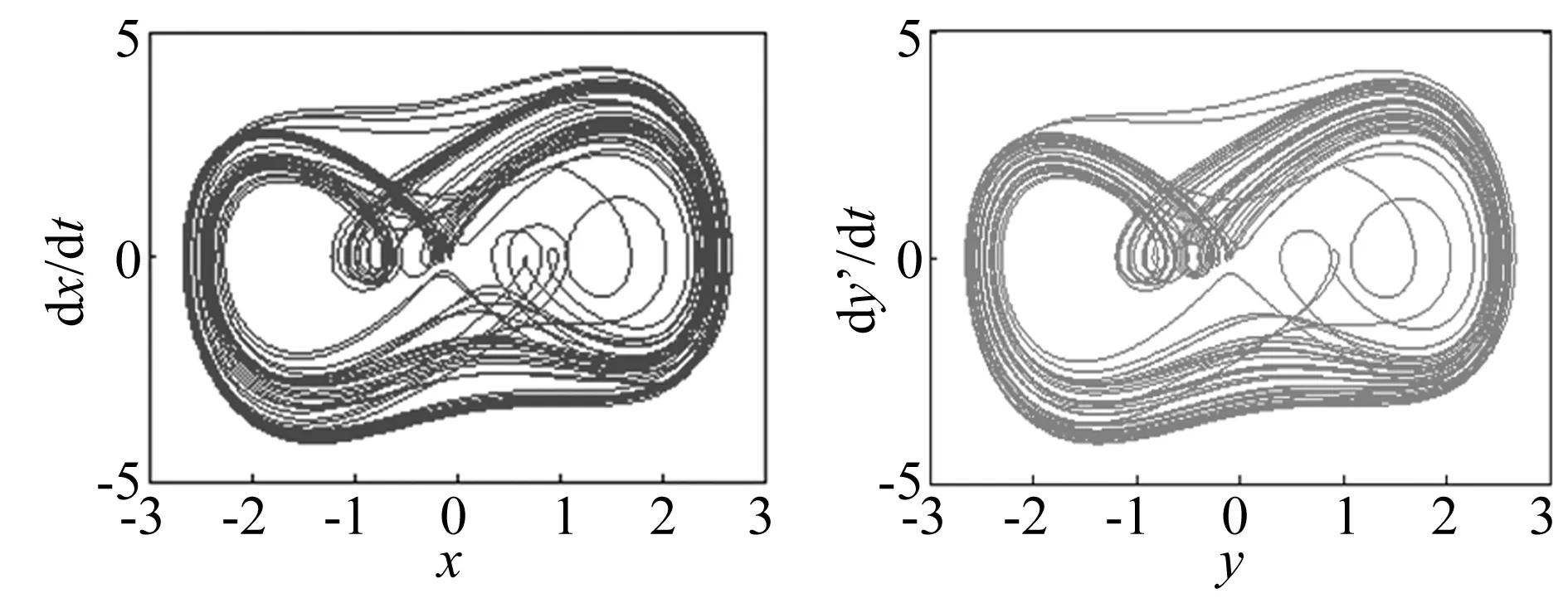
图6　同步后两系统的二维相图(左为DVP，右为受控Duffing)Fig.6 2D-phase-trajectory diagrams of two systems after synchronization(DVP in the left, Duffing under the control in the right)

图6表明：如果不计系统误差，Duffing系统的吸引子转变为了DVP系统的“蚕豆”型吸引子，说明两种系统已经达到了精确同步。

4结论

本文通过理论分析和数值仿真，可以得到如下结论：

(1) 考虑结构的几何非线性，分析了受扰复合材料层合梁的非线性振动，利用里兹—伽辽金法得到了与其控制方程等价的Duffing振子方程。

(2) 通过Matlab进行数值仿真，得到：Duffing系统和DVP系统的四个误差函数在经历了一段时间后，都稳定在零点，且e3和e4的时间要短，大概在5 s左右的时间趋于零点；而前两个误差函数e1和e2在25 s左右的时间才趋于零点，这可能与后两项同为正余弦函数，短周期内容易耦合达到同步有关。之后随着时间变化，误差曲线保持水平直线，中间无任何突变或跳跃，因此可以判定Duffing系统和DVP系统实现了异结构的精确混沌同步。

(3) 三维空间相图的t轴是时间轴，该轴与其他任意两轴分别可以组成位移和速度的时程曲线图，时程曲线图如果不是周期性分布，而是无规律的，则说明系统发生了混沌，因此三维空间相图可以更加全面的反映两种系统的混沌运动过程。通过观察可知，经过短暂的变化后，Duffing系统的轨迹变成了和DVP系统完全相同的“蚕豆”型吸引子，说明驱动系统和响应系统达到了同步。

参 考 文 献

[1] Liu Yang-zheng,Jiang Chang-sheng. Chaos switch-synchron-ization for a class of 4-D chaoticsystems[J].Acta Physica Sinica,2007,56(2):707-712.

[2] Maggio G,Rulkov N,Reggiani L. Pseudo-chaotic time hopping for UWB impulse radio[J]. IEEE Trans on Circuit and System,2001,48(12):1424-1434.

[3] Fridrich J,Goljan M. Protection of digital images using self embedding[EB/OL] http://Proc of IC IP99,1999.

[4] Pecora L M,Carroll T L. Synchronization in chaotic systems[J].Physical Review Letters,1990,64(8):821-827.

[5] Kocarev L,Parlitz U. General approach for chaotic synchroni-zation with applications to communication[J].Phys.Rev.Lett,1995(74):5028-5031.

[6] Pyragas K. Experimental control of chaos by delayed self-controlling feedback[M]. Phys.Lett.A,1993(181):203.

[7] Mainieri R,Rehacek J. Projective synchronization in three-dimensional chaotic systems[J]. Phys.Rev.Lett,1999,82(15):3042-3045.

[8] Yan J P,Li C P. Generalized projective synchronization of a unifiedchaotic system[J]. Chaos Solitons and Fractals,2005,26(4):1119-1124.

[9] Hu Man-feng,Xu Zhen-yuan.Full state hybrid projective synchro-nization in continuous-time chaotic (hyperchaotic)systems[J]. Communications in Nonlinear Science and Numerical Simulation,2008,13(2):456-464.

[10] 闵富红,王执铨. 两个四维混沌系统广义投影同步[J].物理学报，2007，56(11)：6238-6244.

MIN Fu-hong,WANG Zhi-quan. Generalized projective synchro-nization of two four-dimensional chaotic systems[J]. Acta Physica Sinica,2007，56(11):6238-6244.

[11] 闵富红,王执铨,史国生. 新型超混沌系统的改进自适应广义投影同步[J].系统仿真学报,2008,20(14):3785-3789.

MIN Fu-hong,WANG Zhi-quan,SHI Guo-sheng.Adaptive modified generalized projective synchronization for new Hyper-cha-otic systems[J]. Journal of System Simulation,2008,20(14):3785-3789.

[12] 王宇野,许红珍. 异结构不确定混沌系统的广义投影同步[J]. 系统工程与电子技术，2010(2):355-358.

WANG Yu-ye,XU Hong-zhen.Generalized projective Synchron-ization between two different uncertain chaotic systems[J]. Systems Engineering and Electronics,2010(2):355-358.

[13] 冯浩,杨洋. Chen系统和Liu系统的广义投影同步的电路仿真设计[J]. 河北北方学院学报:自然科学版，2013,29(5):14-17.

FENG Hao,YANG Yang.Circuit simulation design of generali-zed projective synchronization of Chen system and Liu system[J]. Journal of Hebei North University:Natural Science Edition,2013,29(5):14-17.

[14] 杨洋. 混沌系统全状态混合投影同步研究[D].石家庄:河北师范大学,2007.

[15] 陈启宗. 线性系统理论与设计[M]. 北京：科学出版社,1980.

Chaotic synchronization of a geometric nonlinear composite beam under horizontal-vertical excitations

WANG Long-fei1, HAN Zhi-jun1, YAN Xiao-peng1, LU Guo-yun2

(1. College of Mechanics, Taiyuan University of Technology, Taiyuan 030024, China;2. College of Architecture and Civil Engineering, Taiyuan University of Technology, Taiyuan 030024, China)

Abstract:Based on Ritz-Galerkin Method, the dynamic governing equations of a composite beam with clamped-fixed boundary conditions were simplified into the typical Duffing equations considering geometric nonlinear. A Duffing-Van Der Pol System was introduced. Parameter values of two systems reaching chaotic state commonly were presented according to their bifurcation diagrams. The accurate synchronization between Duffing system and DVP System (short for Duffing-Van Der Pol) was realized using the generalized projective synchronization method and their synchronization’s controller was also acquired. Finally, numerical simulations for chaotic synchronization of the two systems were conducted with Matlab and synchronous error curve diagrams, 2D-phase-trajectory diagrams, 3D-phase-trajectory diagrams of the two systems were obtained. These diagrams were used to verify the correctness of chaotic synchronization.

Key words:composite; chaotic synchronization; DVP system; generalized projective synchronization method

基金项目：国家自然科学基金(11372209)；山西省自然科学基金(2013011005-1)

收稿日期：2015-03-18修改稿收到日期：2015-05-13

通信作者韩志军 男，博士，教授，1964年10月生

中图分类号:TB33；O322

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.005

第一作者 王龙飞 男，硕士生，1988年3月生