一种基于Delaunay三角剖分的特征点坐标对应方法

徐　侃　李文龙,2　王建庄　周莉萍　尹周平,2

1.华中科技大学数字制造装备与技术国家重点实验室，武汉，4300742.广东华中科技大学工业技术研究院，东莞，523808

一种基于Delaunay三角剖分的特征点坐标对应方法

徐侃1李文龙1,2王建庄1周莉萍1尹周平1,2

1.华中科技大学数字制造装备与技术国家重点实验室，武汉，4300742.广东华中科技大学工业技术研究院，东莞，523808

摘要：研究了平面网格点集的Delaunay三角剖分性质，提出ACDT方法，并在IC封装环境下实现了圆点阵列靶标特征点的自动对应。实验结果表明，当图像存在拍摄倾角或由靶标平移、旋转引起的特征点缺失时，该方法仍可有效运行，且对镜头畸变引起的图像非线性变形不敏感，特别适合IC封装视觉定位系统的在线标定。

关键词：圆点阵列靶标；在线摄像机标定；Delaunay三角剖分；特征点对应

0引言

视觉定位因其非接触、高精度、无损伤等优点，在IC封装设备上得到广泛应用[1-3]。圆点阵列型靶标将圆形区域中心作为特征点，相比于棋盘格型靶标具有更高的标定精度[4-6]，因而在IC封装设备上被广泛应用[7]。

摄像机标定过程中，特征点图像坐标的提取顺序常常与其阵列分布的顺序不一致，传统方法需要加入不同程度的人工干预(调整标定位置，人工统计特征点网格的行数、列数等)，以保证标定特征点的图像坐标与世界坐标的正确对应，显然这会影响设备的工作效率。针对IC封装设备在线、全自动运行的要求，以尽可能减少IC封装设备摄像机标定过程中的人工干预为目的，国内外研究者提出了多种特征点自动对应方法。文献[8]提出一种基于RADON变换的智能感兴趣区域方法，可实现阵列圆点靶标上特征点图像坐标与世界坐标的自动对应，但它只能在拍摄倾角小、图像采集系统畸变小的前提下有效。文献[9-10]提出的方法都只对右上角带有特殊三角形标记的特制标定板有效。文献[11]所述方法允许特征点网格存在一定程度的残缺，但必须保证特征点网格外围至少有一条边是完整的。

尽可能少的人工干预以及尽可能高的镜头畸变适应性成为了IC封装设备摄像机标定算法继续研究的努力方向，为此，本文提出一种基于Delaunay三角剖分的ACDT(automatic correspondence based on Delaunay triangulation)方法。

1特征点图像坐标提取

1.1有效靶标区域筛选

本文联合使用区域面积与区域相对圆度两个条件，筛选有效靶标区域。区域面积可近似等于组成该区域的像素点个数。依据GB/T 1958-2004《形状和位置公差检测规定》中关于圆度评定的最小区域圆法计算区域的相对圆度。假设区域轮廓点的图像坐标为(xi，yi)，以

F(a，b)=max(di)-min(di)

(1)

为目标式进行无约束的非线性优化计算，令F(a，b)最小时图像坐标(a，b)的取值为(a0，b0)，将其作为该区域的最小条件圆心图像坐标。其中，图像坐标(a，b)的初值选择区域重心点的图像坐标为(xc，yc)。将(a0，b0)代入式(1)，计算区域相对圆度：

(2)

实际操作过程中，只需根据标定靶标的成像情况选择合适的区域面积阈值与区域相对圆度阈值，就能在完整保留有效靶标区域的前提下去除所有干扰区域。图1a为一幅800像素×800像素的标定图像，观察发现，每个标定靶标区域成像的直径约为85个像素，面积约为5671像素。据此，设定面积高低阈值分别为6000像素、5000像素，相对圆度阈值为0.2，进行有效靶标区域筛选，结果如图1b所示。

(a)标定图像(b)筛选结果图1　有效靶标区域筛选示例

由于多数IC封装设备视觉系统的物距是固定的，故可将设备常用标定标靶的区域面积筛选阈值和区域相对圆度筛选阈值存储起来。当更换标定标靶时，由设备程序自动载入对应的筛选阈值信息，从而在不停机、无人工干预的前提下，自动完成特征点区域的分割，提高设备运行效率。

1.2特征点图像坐标计算

IC封装设备视觉系统采集对标定靶标的成像过程中不可避免地引入一定程度的倾斜误差，使得靶标区域在摄像机CCD平面上的成像为椭圆。将有效靶标区域的轮廓点坐标(xi，yi)代入椭圆方程，组成以椭圆方程参数A、B、C、D、E、F为未知数的方程组。靶标区域轮廓点多于6时，该方程组超定。

方程组残差的平方和为

(3)

计算使得Z取最小值时，方程组参数的最小二乘解a、b、c、d、e、f(分别对应方程组中的未知数A、B、C、D、E、F)，代入下式

(4)

计算该区域轮廓的中心图像坐标(x0，y0)。

需要注意的是，当有效靶标区域的轮廓与图像边界重合时，图像边界上的有效靶标区域轮廓点不参与上述的椭圆拟合计算，以保证特征点图像坐标的提取精度不受到影响。

2特征点图像坐标与世界坐标对应

2.1四邻域信息表建立

如图2所示，对于由特征点集P组成的平面网格(特征点网格)ξ中任意一点Pi，定义在ξ的行列方向上与Pi相邻的点Pij为Pi的四邻域点，向量PiPij与水平向右方向所成夹角θij(取值范围0°～360°)为Pij相对于Pi的方向角。特征点网格ξ的四邻域信息表记录了其中点Pi的四邻域点Pi1、Pi2、Pi3、Pi4及其对应的方向角θi1、θi2、θi3、θi4。

图2　特征点网格四邻域信息的定义

2.1.1筛选有效剖分三角形

受摄像机镜头光学畸变的影响，标定图像不可避免地存在一定程度的非线性变形，其中，摄像机镜头的一阶径向畸变起主要作用。为简化起见，可认为图像非线性变形全部来自于摄像机镜头的一阶径向畸变[12-13]，其数学模型为

(5)

式中， (ru，cu)、(rd，cd)分别对应畸变前后图像上某一点的图像坐标；(r0，y0)为畸变主点的图像坐标；k为图像采集系统的一阶径向畸变系数。

512像素×512像素图像上以坐标(64，64)为起点，长384个像素、宽384个像素的区域内均布着5像素×5像素的标准平面网格，以图像中心为畸变主点，按照式(5)对上述标准平面网格加入畸变系数k=2.5×10-6的非线性变形，得到仿真特征点网格。对变形后的平面网格进行Delaunay三角剖分，结果如图3a所示。可以发现，变形后的网格Delaunay三角剖分结果中出现了图3b所示的奇异剖分三角形。根据奇异剖分三角形无法正确建立该网格的四邻域信息表，需要通过筛选将奇异剖分三角形去除。

(a)Delaunay剖分三角形(b)奇异剖分三角形图3　剖分三角形及其中的奇异三角形

定义一种形状偏差角：

η=max(η1，η2，η3)

(6)

ηi=min(|ωi-45°|，|ωi-90°|)i=1，2，3

式中，ω1、ω2、ω3分别为三角形的3个内角。

η用于衡量一个三角形与直角三角形在形状上的近似程度，η越小，越接近直角三角形。

对上述标准平面网格，分别加入畸变系数k1=2.5×10-6，k2=-2.5×10-6的非线性变形。|k|=2.5×10-6时，网格点(64，64)在图像上的变形量已达到约50个像素，远超过测量用图像采集系统最大畸变不超过1%的要求。

记录上述两种非线性变形下Delaunay三角剖分结果中有效剖分三角形形状偏差角的最大值ηemax与奇异剖分三角形形状偏差角的最小值ηimin，如表1所示。需要说明的是，k<0对应的畸变网格不存在奇异剖分三角形，故表中k2对应的ηimin不存在。由表1可以看出，ηemax与ηimin差距明显。由此可见，以形状偏差角η作为筛选条件可达到理想的区分效果。实际应用中，根据实际图像采集系统的畸变程度，设定合适的形状偏差角阈值η0(一般不超过20°)筛选有效剖分三角形。

表1　有效、奇异剖分三角形η的比较　(°)

2.1.2有效剖分三角形的性质

设定形状偏差角阈值η0=15°对图3a中的剖分三角形进行筛选，结果如图4a所示。可以发现，有效剖分三角形非最长边呈现如下两个性质：

性质1有效剖分三角形非最长边的端点都是特征点网格中的一对四邻域相邻点对。

性质2特征点网格中任意一对四邻域相邻点对构成的线段，至少构成一个剖分三角形的非最长边。

上述性质说明，特征点网格所有有效剖分三角形非最长边构成的线段集合与其所有四邻域相邻点对构成的线段集合相等。遍历有效剖分三角形的非最长边的端点，将它们的点序号及方向角分别加入到对方的四邻域信息中，可以建立特征点网格的四邻域信息表。根据图4b所示的有效剖分三角形非最长边建立仿真网格的四邻域信息表，其中序号1～7的部分见表2。

(a)有效剖分三角形

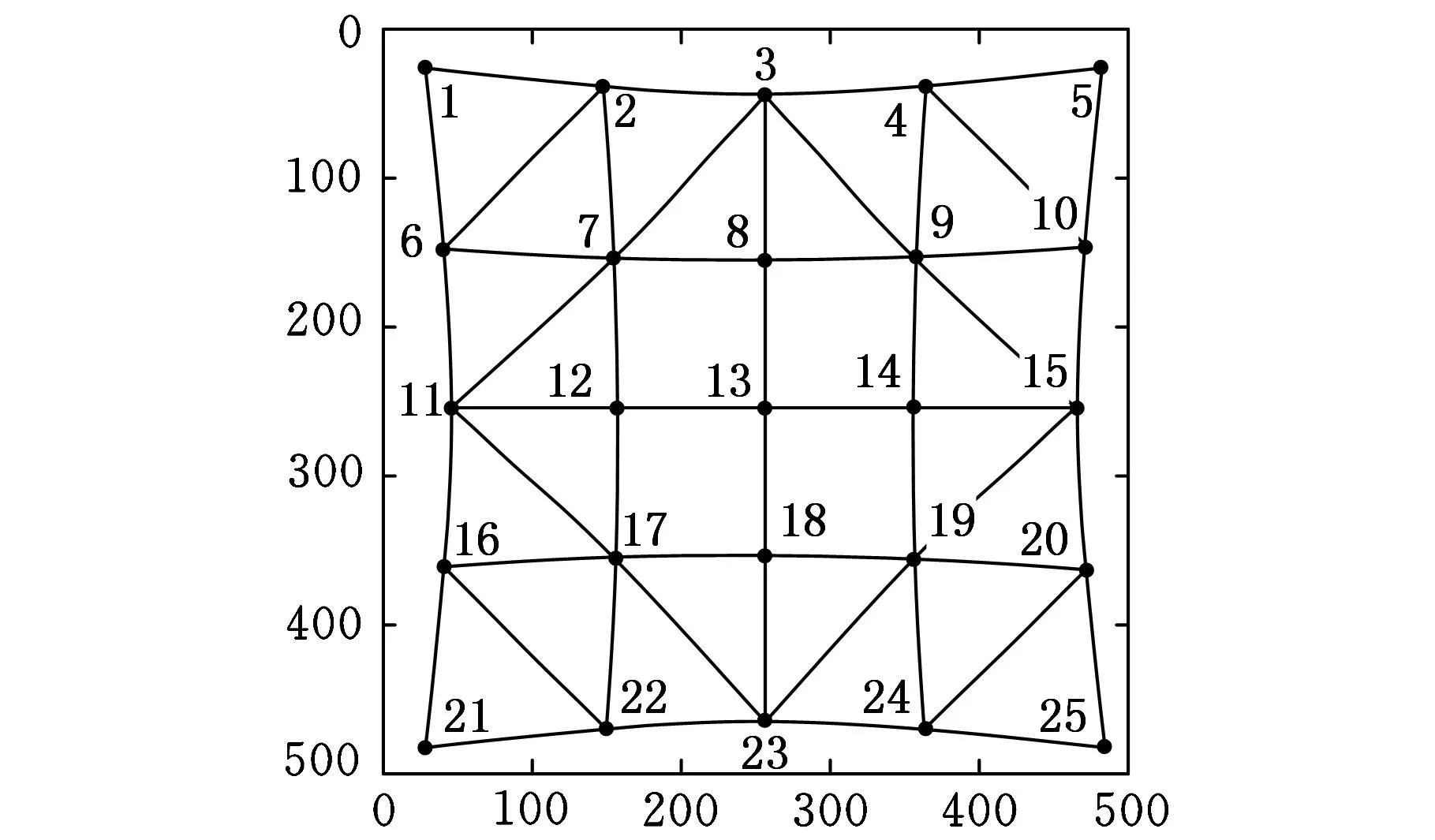
(b)非最长边图4　有效剖分三角形及其非最长边

2.2特征点坐标对应

四邻域递归搜索是一种图像连通域遍历的常用方法，从图像连通域中任意一点出发，递归搜索当前点的四邻域点，可以保证遍历图像连通域的所有点。圆点阵列靶标特征点的分布与一个图像连通域的像素点分布类似，故可将四邻域递归搜索用于特征点集的遍历。在该遍历过程中，根据递归搜索路径可以确定每一点相对种子点的网格坐标，进而得到特征点集中所有点的世界坐标。

表2　仿真特征点网格的四邻域信息表(部分)

2.2.1特征点集遍历方法

本文约定用字母n表示递归层数序号，设第n层递归的当前点Pn在特征点网格ξ的行正、列正、行负、列负方向上的四邻域点及其方向角分别为PnR+、PnC+、PnR-、PnC-和θnR+、θnC+、θnR-、θnC-。任选特征点集P中一个点P0作为种子点，然后从P0开始进行深度优先的特征点遍历。以Pn为起始点遍历所有特征点(采用了递归的编程思想)的伪代码如下：

DepthFirst_Search(Pn)

{

访问Pn并标记为已遍历

ifPnR+存在且未被遍历

DepthFirst_Search (PnR+)

ifPnR+存在且未被遍历

DepthFirst_Search (PnC+)

ifPnR+存在且未被遍历

DepthFirst_Search (PnR-)

ifPnR+存在且未被遍历

DepthFirst_Search (PnC-)

}

2.2.2遍历过程中的四邻域点位置确定

如图5所示，从特征点网格ξ中的点Pi出发分别到其四邻域点Pi1、Pi2、Pi3、Pi4构成向量PiPi1、PiPi2、PiPi3、PiPi4，αi12、αi23、αi34、αi41分别表示向量PiPi1与PiPi2、PiPi2与PiPi3、PiPi3与PiPi4、PiPi4与PiPi1的夹角，定义ξ的最大畸变角βmax：

βmax=max(βi12，βi23，βi34，βi41)

(7)

式中，βi12、βi23、βi34、βi41分别为角αi12、αi23、αi34、αi41与90°差的绝对值。

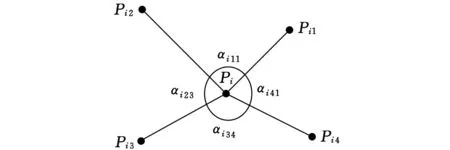
图5　特征点网格的最大畸变角

对均布在512像素×512像素图像上以坐标(64，64)为起点，长384个像素、宽384个像素的区域内不同规格的标准平面网格，分别加入畸变系数k1=2.5×10-6，k2=-2.5×10-6的非线性变形，记录其中每个网格的最大畸变角度βmax，如表3所示。可以看出，在图像存在严重非线性变形的情况下，βmax可以保持在一个较小(不超过10°)的范围内，这种性质称作特征点网格的局部抗畸变性。

表3　不同规格网格的βmax角度值

特征点遍历过程中，仅通过查询四邻域信息表无法确定一个特征点的四邻域点在特征点网格上相对于它的位置。ACDT方法利用特征点网格的局部抗畸变性，不断更新当前特征点对应的局部行、列方向，并基于此确定当前特征点的四邻域点相对于它的位置。

规定种子点的局部行正、列正、行负、列负方向角δ0R+、δ0C+、δ0R-、δ0C-分别为0°、90°、180°、270°。当递归层数n>0时，设向量Pn-1Pn与水平向右方向的夹角为γ，根据Pn相对Pn-1所处位置，查询表4计算Pn的局部行列方向角δnR+、δnC+、δnR-、δnC-，并将它们归一化到0°～360°的范围内。选取合适的方向偏差阈值ε0(一般在20°内)，按下式

(8)

确定Pn的四邻域点Pnj(j=1，2，3，4)相对于Pn的位置。

表4　第n层递归局部行、列方向角的计算方法

2.2.3遍历过程中的世界坐标计算

设第n-1层递归当前点Pn-1相对于种子点P0的网格坐标为(rn-1，cn-1)，特征点遍历过程中，可以根据点Pn相对于Pn-1所处的位置，查询表5计算Pn相对于种子点P0的网格坐标(rn，cn)。

表5　特征点相对网格坐标的计算方法

特征点遍历结束后，找到所有特征点相对种子点的网格行坐标值的最小值rmin与网格列坐标值的最小值cmin，按照下式计算每个特征点Pi的世界坐标(Xi,Yi)。

(9)

式中，L为特征点间距在世界坐标下的对应值。

联系各特征点Pi世界坐标(Xi，Yi)与图像坐标(xi，yi)即可完成特征点坐标对应。

3测试与结果

3.1ACDT方法适应性仿真测试

IC封装设备采用单幅图像实现快速标定，无需求解摄像机的内外参数。为了保证图像区域能够尽可能地被特征点覆盖，用于IC封装设备的标定板一般大于并涵盖了摄像机的视场区域。因此，当标定板相对摄像机出现平移、旋转、倾斜等定位误差时，落在摄像机视场范围内的特征点网格外围往往没有一条边是完整的。另外，镜头畸变也使得特征点网格中同一行、列上的点不再共线。本实验通过仿真生成一个上述情况都存在的点集，测试ACDT方法在恶劣成像条件下，特征点坐标对应功能的适应性。

仿真图像的大小为512像素×512像素，特征点网格ξ0的间距为96个像素、规格为21行×21列，分布在以图像坐标分别为(-896，-896)、(-896，896)、(896，-896)、(896，896)的4个像素点为顶点的正方形区域内。对ξ0加入绕摄像机光轴20°的旋转变换、绕图像水平上边缘逆时针30°的倾斜变换后，取变换后ξ0中落在图像范围内的点集，记为ξ1。按照式(5)对ξ1分别加入畸变系数k1=2×10-6，k2=-2×10-6的非线性变形后，分别取上述两个变形后ξ1中仍落在图像范围内的点集，记作ξ2(对应畸变系数为k1的变形)、ξ3(对应畸变系数为k1的变形)。

对点集ξ2、ξ3进行Delaunay三角剖分，结果分别如图6a、图6b所示。设定形状偏差角阈值η0=20°，从Delaunay三角剖分得到的剖分三角形中筛选形状偏差角小于等于η0的三角形(作为有效剖分三角形)，结果如图6c、图6d所示。去掉各有效剖分三角形的最长边，结果如图6e、图6f所示。不难发现，遍历它们可以建立正确的特征点网格四邻域信息表。

(a)点集ξ2 剖分(b)点集ξ3 剖分

(c)点集ξ2有效剖分(d)点集ξ3有效剖分

(e)点集ξ2非最长边(f)点集ξ3非最长边图6　仿真特征点集的剖分三角形操作

设定方向偏差阈值ε0=20°进行四邻域递归搜索遍历，得到点集ξ2、ξ3中各特征点的网格坐标，如图7所示，至此完成特征点图像坐标与网格坐标的对应。对实际标定特征点集，根据特征点间距的标称值，将特征点网格坐标转换为世界坐标，完成特征点图像坐标与世界坐标的对应。

3.2ACDT方法适应性实验测试

(a)点集ξ2的网格坐标

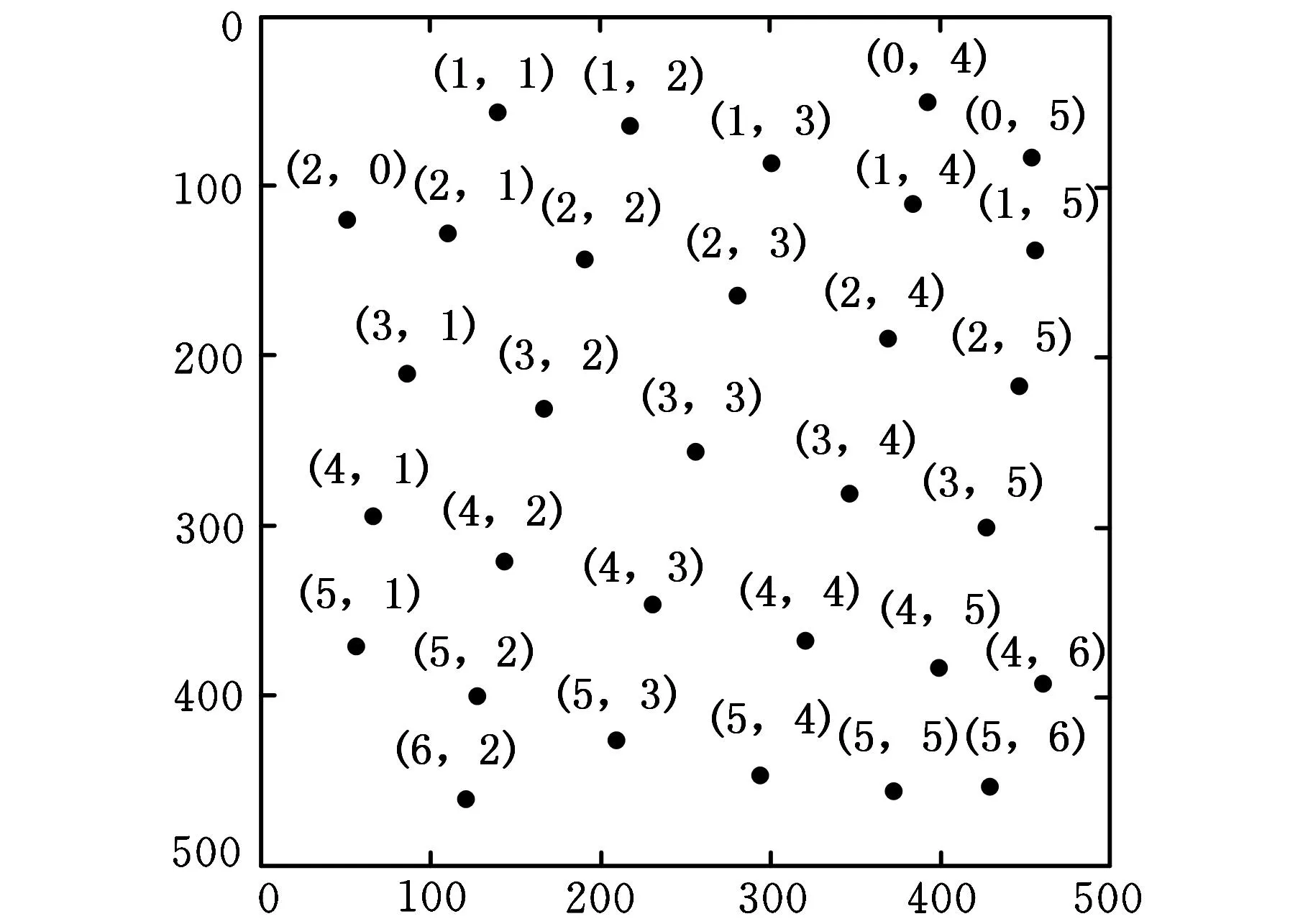
(b)点集ξ3 的网格坐标图7　仿真特征点集中各点的网格坐标

图8a所示的标定图像(800像素×800像素)来自于武汉华威科智能有限公司的HEI-DIII型RFID标签倒装键合机，标定板规格为0.8 mm(特征点间距标称值)。可以看出，标定板位置调整不当导致图像存在干扰区域且特征点网格存在一定程度的倾斜。根据本文所述的方法设定面积高低阈值分别为150、100，相对圆度阈值为0.2，进行有效靶标区域筛选并计算每个有效特征点区域中心的图像坐标，结果如图8b所示。

(a)实验标定图像(b)特征点图像坐标提取结果图8　实验标定图像及其提取得到的特征点

根据本文所述的方法，对图7b中的特征点按照其图像坐标进行Delaunay三角剖分，结果如图9a所示。然后，从得到的剖分三角形中筛选形状偏差角小于等于20°的三角形作为有效剖分三角形，结果如图9b所示。

(a)Delaunay剖分三角形(b)有效剖分三角形图9　特征点集Delaunay三角剖分结果及有效剖分三角形

最后，根据本文所述的方法得到每个有效特征点的图像坐标与网格坐标的对应关系，如表6所示(特征点个数过多，仅列出前5个与最后5个)。

表6　ACDT方法适应性实验测试结果

图8a所示的标定图片无法通过MIL 8.0机器视觉算法软件包制作标定文件。而本文方法在设备上的应用，成功地克服了这一问题，使得设备无需再依靠人工干预调整标定板的位置，提高了在线自动运行的效率。

3.3ACDT方法精度实验测试

图10为用于测试的6张图片，每个标定板都存在一定程度的拍摄倾角(标定特征点在图像平面上的投影为椭圆形)。

(a)测试图像1(b)测试图像2

(c)测试图像3(d)测试图像4

(e)测试图像5(f)测试图像6图10　特征点图像坐标提取精度测试图片

ACDT方法与软件包HALCON对上述图片集特征点图像坐标提取计算结果的偏差如表7所示。可以看出，两种方法提取特征点的图像坐标结果在一个方向的偏差均值不超过0.1个像素，偏差最大值在0.3个像素以内，ACDT方法图像坐标提取精度与现有的成熟商用软件包基本持平。

表7　两种方法提取结果的偏差　pixel

4结论

(1)本文提出了一种基于Delaunay三角剖分、针对圆点阵列靶标的特征点坐标自动对应方法。通过分析特征点集Delaunay剖分三角形的性质，定义了特征点网格的四邻域信息表并提出了它的建立方法。同时，分析了特征点网格的局部抗畸变性质，利用这一性质及四邻域信息表，使用四邻域递归搜索法遍历特征点集并在遍历过程中确定每个点在特征点网格上的位置，完成了特征点图像坐标与世界坐标的对应。

(2)测试结果表明，本文所述方法应用于IC封装设备在线标定时，可以解决一些现有成熟方法无法适应的奇异情况：对图像非线性变形不敏感，无需在靶标区域中设置特殊标记，无需人工调整标定板的放置位置。同时，该方法提取特征点坐标的精度也可与现有成熟算法保持在相同的水平上。

参考文献：

[1]Zhang Kai，Wang Yuhui，Yin Zhoupin. A Fast Vision Alignment in High Performance Chip Mounter[J]. Optical Technique，2005，31(4)：604-607.

[2]Wang Hongsheng，Shi Tielin. High Precision Alignment System Research and Development in Machine Vision[J]. Optical Technique，2004，30(2)：235-239.

[3]Li Junlan，Zhang Dawei，Zhao Xingyu，et al. Micro-vision Positioning Systems for IC Packaging[J]. Optics and Precision Engineering，2010，18(4)：995-972.

[4]Heikkila J. Geometric Camera Calibration Using Circular Control Points[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(11)：1330-1334.

[5]Wang Zhongshi，Xu Xinhe. Auto-recognition and Auto-location of the Checkerboard Pattern Corners[J]. Journal of Image and Graphics，2004，12(4)： 618-622.

[6]张世辉，郭翠翠，孔令富．一种新的基于并联机构的摄像机线性标定方法[J]．中国机械工程，2009，20(14)：1651-1655．

Zhang Shihui，Guo Cuicui，Kong Lingfu. A Novel Linear Approach for Camera Calibration Based on Parallel Mechanism[J]. China Mechanical Engineering，2009，20(14)：1651-1655.

[7]Liang Li，Yin Dongfei，Wang Chuan. Design and Detection Methods for Accurate Cameral Calibration Targets[J]. Journal of Xi’an Jiaotong University，2011，45(4)：82-85.

[8]Kou Xinyu, Wang Zhong，Chen Mingzhou，et al. Fully Automatic Algorithm for Region of Intrest Location in Camera Calibration[J]. Optical Engineering，2002，41(6)：1220-1226.

[9]Yu Chunsheng，Peng Qingjin. Robust Recognition or Checkerboard Pattern for Camera Calibration[J]. Optical Engineering，2006，45(9)：1-9.

[10]夏瑞雪，卢荣胜，刘宁，等．基于圆点阵列靶标的特征点坐标自动提取方法[J]．中国机械工程，2010，21(16)：1906-1910．

Xia Ruixue，Lu Shengrong，Liu Ning，et al. A Method of Automatic Extracting Feature Point Coordinates Based on Circle Array Target[J]. China Mechanical Engineering，2010，21(16)：1906-1910.

[11]谭海曙，周富强，张伟，等. 摄像机标定中特征点的一种自动对应方法[J]. 光电子·激光，2011，22(5)：736-739.

Tan Haishu，Zhou Fuqiang，Zhang Wei，et al. Automatic Correspondence Approach for Feature Points in Cameral Calibration[J]. Journal of Optoelectronics·Laser，2011，22(5)：736-739.

[12]Zhang Zhengyou. A Flexible New Technique for Camera Calibration[J]. IEEE Transactions on Pattern Analysis and Machine Itelligence，2000，22(11)：1330-1334.

[13]Zhou Fuqiang, Cai Feihua. Cameral Calibration Method Based on Non-metric Distortion Correction[J]. Journal of Mechanical Engineering，2009，45(8)：228-232.

(编辑张洋)

A Method of Automatically Extracting and Corresponding Feature Point Based on Law of Delaunay Triangulation

Xu Kan1Li Wenlong1,2Wang Jianzhuang1Zhou Liping1Yin Zhouping1,2

1.State Key Laboratory of Digital Manufacturing Equipment & Technology，Huazhong University of Science and Technology，Wuhan，430074 2.Guangdong HUST Industrial Technology Research Institute,Dongguan,Guangdong,523808

Abstract:Based on the law of Delaunay triangulation applied on 2D grid points, this paper proposed a method called ACDT(automatic correspondence based on Delaunay triangulation) to correspond the feature points for 2D circle array target in IC packaging environment. The experimental results show that the method can still work when there is an affine image distortion caused by oblique view angle, or the lost of feature points caused by offset and rotation of the target. It is not sensitive to the non-linear image distortion caused by lens distortion and most suitable for online camera calibration.

Key words:circle array target; online camera calibration; Delaunay triangulation; feature point corresponding

收稿日期：2015-12-17

基金项目：国家自然科学基金资助项目(51475187，51275192)；广东省引进创新科研团队计划资助项目(2011G006)；国家科技重大专项(2014ZX04001051-05)；中央高校基本科研业务费专项资金资助项目(2015QN051)

中图分类号：TP391.41

DOI：10.3969/j.issn.1004-132X.2016.01.002

作者简介：徐侃，男，1988年生。华中科技大学数字制造装备与技术国家重点实验室硕士研究生。主要研究方向为视觉定位。李文龙(通信作者)，男，1980年生。华中科技大学机械科学与工程学院副教授，广东华中科技大学工业技术研究院工程师。王建庄，男，1982年生。华中科技大学机械科学与工程学院讲师。周莉萍，女，1965年生。华中科技大学机械科学与工程学院教授。尹周平，男，1972年生。华中科技大学华中科技大学机械科学与工程学院教授，广东华中科技大学工业技术研究院工程师。