海上漂浮式风电机组风波载荷计算与分析

刘德顺　刘子其　戴巨川　龙　辛

1.湖南科技大学，湘潭,4112012.海上风力发电技术与检测国家重点实验室，湘潭,411102

海上漂浮式风电机组风波载荷计算与分析

刘德顺1刘子其1戴巨川1龙辛2

1.湖南科技大学，湘潭,4112012.海上风力发电技术与检测国家重点实验室，湘潭,411102

摘要：以海上大型漂浮式风电机组三浮桶式支撑结构为对象，考虑风波联合作用，借助叶素-动量理论和线性波理论，联合风载荷和波浪载荷模型构建了风波联合载荷模型。计算过程中，考虑了风电机组不同的运行工况，依据浮桶直径与波长的比值来确定波浪载荷适用的计算模型(Morison理论与绕射理论)；得到了不同工况、不同环境参数和结构参数条件下的载荷结果，分析了风波载荷的变化特征。

关键词：漂浮式风电机组；风波载荷；叶素-动量理论；线性波理论

0引言

随着陆地风电场不断开辟，剩余陆地风资源日益减少，风电场向海上扩展成为必然。同时，海上风电场具有风力资源大，风湍流强度和海面粗糙度更小等优点。目前，各国海上风电场以近海风电场为主，深海风电场由于采用复杂的漂浮式结构还处于探索阶段，仅有少量样机出现。相比于陆上风电机组，海上风电机组服役环境更加恶劣，除了风载荷以外，还要承受复杂的波浪载荷，而且两者之间是相关的。长期以来，有关风波载荷分析一直是各学者研究的热点问题， Moriarty等[1]、Buhl等[2]采用平均风速和湍流度联合分布的方式，借助FAST_AD代码得到载荷数据，建立了极端风载荷参数化模型；Karimirad等[3]基于Simo/Riflex代码(采用的波浪载荷Panel模型考虑的是一阶波浪载荷，并通过延迟函数计及表面记忆效应)进行了波浪力计算；Henderson等[4]基于线性波理论对随机波浪载荷进行计算，采用非线性波理论对极端波浪载荷进行了分析；Peeringa等[5]基于Morison方程进行了波浪载荷计算，并开展了室内测试与分析；徐建源等[6]针对桩式近海风电机组，利用叶素-动量理论建立了风载荷模型，根据Morison方程建立了风电机组波浪载荷模型，用以研究结构动力响应；陈小波等[7]基于Morison方程和流函数理论计算了近海风电机组非线性波浪载荷，并与线性波浪载荷进行了对比分析；Seidel等[8]借助商业化软件Reflex和ASAS(NL)对海上单桩基础风电机组的风波载荷进行了初步分析。虽然各国学者从不同角度开展了海上风电机组载荷的研究工作，但相关研究还有待深入。主要问题包括：①风载荷与波浪载荷往往独立计算与分析，没有考虑到风波载荷的相关性；②针对海上漂浮式风电机组的系统研究还没有形成；③载荷计算时，对风电机组运行工况考虑不够；④多采用同一公式计算不同结构参数时的波浪载荷，没有考虑结构尺寸、波浪参数变化时公式的适用性等问题。因此，笔者以2MW海上漂浮式风电机组支撑结构为研究对象，考虑风波载荷的相关性，分析不同运行工况，不同结构参数以及不同风速、水深等环境参数条件下风波载荷特性。

1漂浮式风电机组结构

目前，大型海上漂浮式风电机组支撑结构的主要形式有三浮体结构、Spar结构和张力腿结构，如图1所示。图1a所示为三浮体结构，该结构通过连接杆把3个直立浮桶连接起来，利用其大平面的重力扶正力矩使整个平台稳定，优点是结构简单、经济性较好，缺点主要是泊系统的复杂性。图1b所示为Spar结构，它利用浮力罐底部的配重实现平台稳定，优点是结构简单，缺点是其较多的自由度和大的位移量需要更重的压载物作配重。图1c所示为张力腿结构，浮桶受到的水平方向波浪载荷要比垂直方向的大，通过张力腿的张力实现平台的稳定，优点是稳定性好，缺点是需要产生远大于结构自重的浮力，张力腿一直处于绷紧状态，设计较为复杂。在上述几种结构中，三浮体式结构简单，后期安装、维护方便，故主要针对该结构进行载荷分析。

(a)三浮体结构　　(b)Spar结构(c)张力腿结构图1　风电机组浮式结构示意图

2线性波基本理论

对波浪描述的有效方法主要有线性波理论和非线性波理论(Stokes非线性波理论、椭圆余弦浅水非线性波理论等)。非线性波能更好地反映波浪的波动特性，但是计算过程复杂。在工程计算中，线性波理论方法简单、计算效率高，而被广泛应用。

图2所示为一种简化的线性波波面，图中，d为水深；L为波长，L=2π/k；k为波数；H为波高；T为周期定义，T=2π/ω；ω为波的角频率。线性波用余弦形式表示为

η=Acos(kx-ω t)

(1)

式中，A为幅值；t为时间。

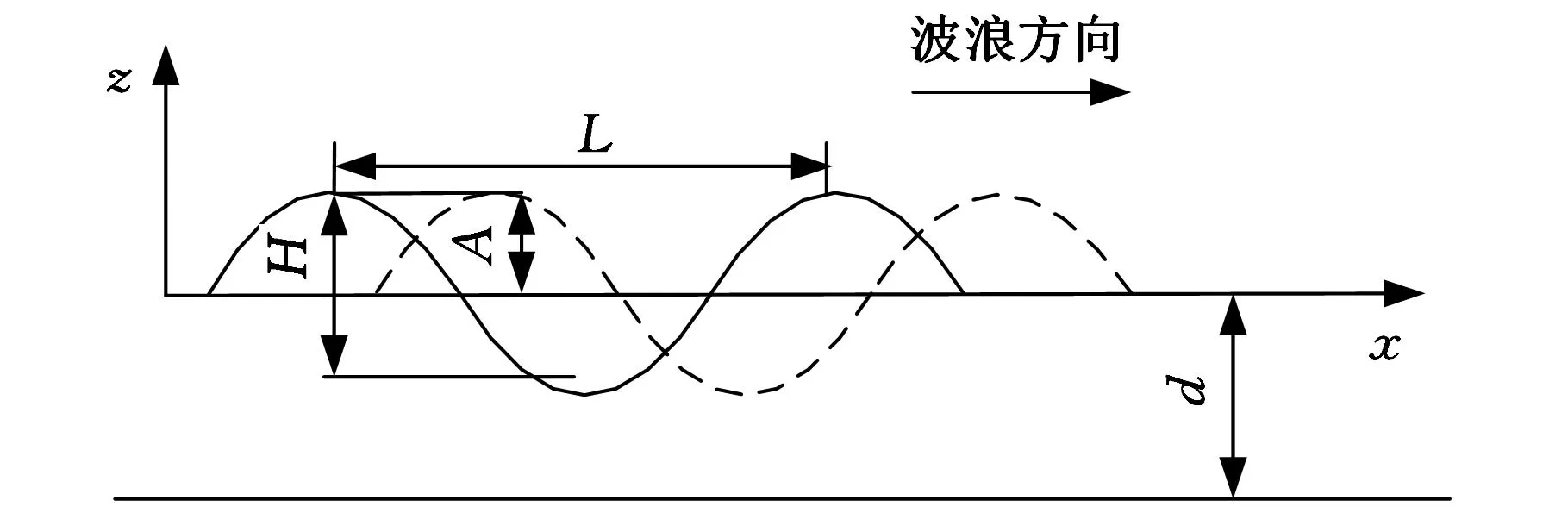
图2　线性波波面示意图

根据波浪理论，二维线性波运动的基本方程和边界条件为

(2)

(3)

式中，Φ为速度势；uz为z方向上流体的速度分量；g为重力加速度。

水质点运动时，x方向速度为[9]

(4)

式中，γ为波浪的传播方向与x轴的夹角。

水质点运动时，x方向加速度为

(5)

3风波载荷计算模型

3.1风波关系模型

太阳对地球表面的空气不均匀加热形成风，在风的作用下，海水离开原来的平衡位置，发生向上、向下、向前和向后方向运动，形成波浪。可以将波浪视为平稳的随机过程，用波谱来描述其组成，常见的波谱有Neumann谱、Bretschneider(布氏)谱、Mitsuyasu(光易)谱、P-M谱[10]。这些波谱模型基于实测统计，通过半经验、半理论分析得出。P-M谱是海洋工程中运用最广的波谱，其表达式为

(6)

式中， Sη η为谱函数； Hs为有效波高；T0为跨零周期； v19.5为海平面上19.5m处的风速[11]。

由式(6)可以看出，波浪的高度和周期均受到风速大小的影响，两者具有密切的相关性。

3.2风载荷模型

3.2.1正常发电工况

风轮旋转过程中，承受的风载荷采用叶素-动量理论(bladeelementmomentumtheory，BEM)进行计算。根据BEM理论[12-14]，作用在叶素上气动力dFR可分解为轴向力分量dFN和切向力分量dFQ：

(7)

风轮的气动载荷如图3所示，其中，α为攻角，β为桨距角，dFL为升力，dFD为阻力。

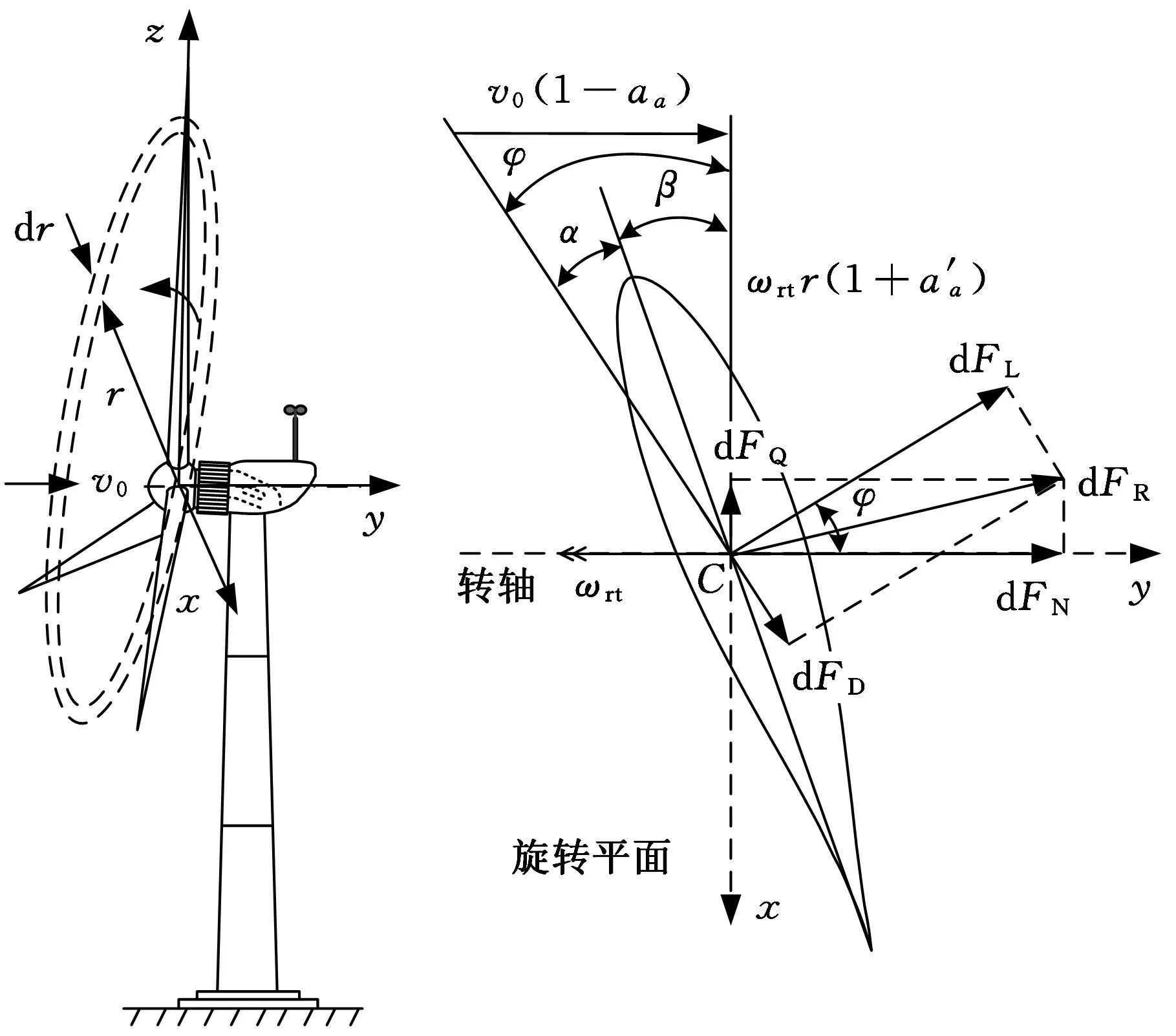
(a)叶素扫出的圆环(b)叶素的速度和作用力图3　风轮的气动载荷

作用在轮毂处的水平推力矩为

(8)

式中，R为叶片长度；Ft为叶片推力；h0为轮毂中心距地面高度；θw为风轮方位角；v为风轮中心高度h0处的来流风速；λ为风速廓线指数。

3.2.2停止发电工况

风电机组停止发电时，作用在风轮固态面积上的平均压力为

pt=CDDv2

(9)

式中，CDD为阻力系数，CDD=1.1Pa·s2/m2。

作用在轮毂处的水平风力为[15]

(10)

式中，S0为风轮固态面积(叶片在旋转平面上的投影面积之和)，m2；Df为叶片的直径，m。

3.3波浪载荷模型

3.3.1小尺寸构件

海洋工程中，D/L≤0.2(D为浮桶直径)的构件称为小尺寸构件，波浪对结构物的作用主要为黏滞效应和附加质量效应，波浪载荷的计算可以采用Morison方程。Morison方程是一种带有经验性的半理论公式，它包含拖曳力和惯性力，其基本思想就是把波浪力分成同速度的平方成正比的阻力项、同加速度成正比的惯性力项。

作用在支撑结构上的水平方向上的波浪载荷为[16-17]

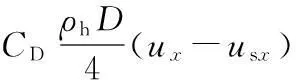
(11)

式中，CD为拖曳力系数；ρh为海水的密度；A为垂直于波浪传播方向的单位柱体高度的投影面积；CM为质量系数；usx为水平方向上塔架的速度；∂usx/∂t为水平方向上塔架的加速度。

在图4中，把塔架看作静态的，可根据式(11)计算某一段柱体(d0～d1)上的水平波浪力：

CDρhDH2(K1-K3)cosθ|cosθ|/2+

CMρhπD2H(K2-K4)sinθ/8

(12)

K2=tanh(kd1)K4=tanh(kd0)

θ=kx-ω t

图4　小尺寸构件波浪力计算模型

显然，式(12)求得的值与参数θ有关系，结合式(11)，可以分别得到水平拖曳力和水平惯性力的最大值：

FDmax=CDρhDH2(K1-K3)/2

(13)

FImax=CMρhπD2H(K2-K4)/8

(14)

事实上，式(13)、式(14)成立时，位相角θ取值不同。

3.3.2大尺寸构件

在海洋工程中， D/L>0.2的构件称为大尺度构件。此时，波浪同结构物之间将会有明显的反射效应和绕射效应，而黏滞效应是相对较小，可以忽略不计。

根据海洋工程波浪力学基本理论，图5中波动场沿x轴正向传播的入射势ΦI和绕射势ΦD为[18]

(15)

式中，Jm(krz)为变量krz的m阶第一类Bessel函数； Hm(krz)为第一类Hankel函数，Hm(krz)=Jm(krz)+iYm(krz)；Ym(krz)为变量krz的m阶第二类Bessel函数；Bm为待定系数；a为浮桶的半径。

图5　大尺寸构件波浪力计模型

波动场总速度势可写为

(16)

将式(16)代入伯努利方程p=-ρh∂Φ/∂t，得到波动场中的压力：

(17)

将压力p沿圆柱周线积分，可得任一到高度z处顺向波的波浪力[18]：

(18)

式中，α为位相滞后角。

不考虑相滞后角，有A(ka)=0.25πCM(ka)2成立，将其代入式(18)，并从z=d0到z=d1积分，有

(19)

在sinω t=1时，式(22)可改写为

3.4风波载荷的联合作用

海上漂浮式风电机组在运行过程中，同时受到风载荷和波浪载荷，严重影响其运行稳定性。一般在浮桶底部设有系泊线以稳定风电机组，结合动态水位调节设施(浮桶内)确保风电机组处于稳定非倾斜状态。外部载荷作用下，风电机组三浮桶支撑结构运动模态分别为平动的纵荡、垂荡、横荡和旋转的首摇、纵摇、横摇，如图6所示。图6中，选定固定在物体平均位置上的右手坐标系xyz，原点在未受扰动的自由液面上，x轴正方向为波浪的传播方向，y轴与波浪传播方向垂直，z轴垂直向上穿过物体的重心。三浮桶六自由度的运动方程为

(20)

图6　运动状态下飘浮平台示意图

在进行载荷分析时，忽略在风波载荷作用下的运动，两种典型的受力情况如图7所示。图7中，G1、G2、G3分别为浮桶1、2、3的重力，Ff1、Ff2、Ff3分别为浮桶1、2、3所受的浮力。

(a) 风载荷与波浪载荷方向相同

(b) 风载荷与波浪载荷方向相反图7　稳定状态下飘浮平台受力分析

图7a所示为风载荷与波浪载荷方向相同的情况，风载荷和波浪载荷产生的浮桶1底部力矩Mz可以由风推力力矩和波浪力矩表示为

Mz=Mf+MH1=Ft(Ht+ht)+

(21)

式中，Mf为风推力力矩；MH1为作用在浮桶1上波浪力矩；Ht为塔架高度；ht为浮桶高度；d0为浮桶离海底的距离。

图7b所示为风载荷与波浪载荷方向相反的情况，风载荷和波浪载荷产生的浮桶1底部力矩Mz可以由风推力力矩和波浪力矩表示为

(22)

4计算结果及分析

根据上述分析，得到风波载荷联合计算流程，如图8所示。计算用风电机组功率为2MW，风轮直径为88m，塔架高度为77.5m，底端直径为4.4m，壁厚为0.06m。在进行风波载荷计算时，载荷大小不仅与外部环境参数有关系，还与风电机组运行状态有关。在来流风速低于风电机组设定额定风速时，风电机组的桨距角不变，通过调整风轮转速(最佳叶尖速比)来获得最大的风能利用系数。在风速高于额定风速时，风轮转速保持不变，通过改变桨距角来控制风轮的能量捕获。

图8　风波载荷计算流程

图9给出了计算用风电机组风轮运行特性曲线。从图9可以看出，当风速小于10.5m/s时，桨距角保持0°不变，风轮的转速随着风速的增加而增加，最大值为1.99rad/s；当风速大于10.5m/s，桨距角随着风速的增大而增大，风轮转速保持1.99rad/s不变。

(a)风速与转速的关系

结合强度和气动的综合考虑，风力机叶片一般包含多种翼型，本文在不同叶片展向长度上分别采用三种不同翼型，如图10a所示，三种翼型所对应的气动参数如图10b～10d所示。

(a) 叶片翼型分布区域

(b) NACA63-421翼型升力、阻力系数

(c) NACA63-418翼型升力、阻力系数

(d) NACA63-415翼型升力、阻力系数图10　叶片翼型分布及升力、阻力系数

图11a所示为正常发电和停止发电两种情况下风载荷的计算结果。在额定风速以下时，风轮上产生的推力随着风速的增加而增加，在额定风速10.5m/s时达到最大推力为279kN。在额定风速以上时，随着风速的增加，风电机组变桨距、桨距角增大，风轮上产生的推力减小，切出风速25m/s时产生的风轮推力为63kN。在风电机组停止发电时，设叶片不再旋转且处于顺桨状态，此时叶素-动量理论已经不在适用，按式(10)计算得到，25m/s时的风轮推力为48kN，43m/s时的风轮推力为146kN。图11b、11c分别给出了单个叶片和整个风轮作用在轮毂上的推力，其中横坐标为风轮方位角，计算条件为v=10.5m/s，ωrt=1.99rad/s，β=0°，h0=90m，λ=0.2。从图11b可以看出，作用在轮毂上的单个叶片推力呈近似正弦曲线变化，这是由于风切变和风轮方位角变化的影响，其变化幅度为18.2kN。3个叶片上的推力合成为风轮推力后，同样呈近似正弦曲线变化(图11c)，但变化频率增加3倍，其变化幅度为450N。不难看出，3个叶片推力合成后，其变化幅度明显减小。

(a)风轮推力随风速变化曲线

(b)单个叶片推力曲线

(c)风轮推力曲线图11　风载荷计算结果

图12所示为风速与D/L的关系。图12a为浮桶直径D一定，水深d1=20 m，30 m，40 m时，风速与D/L关系曲线图。D/L决定了波浪力适用的计算模型。从图12可以看出，水深的变化对D/L的影响比较小，风速对D/L的影响比较明显，总体趋势是随风速的增加，D/L逐渐减小。当风速小于10 m/s时，D/L>0.2，波浪力模型应选择大尺寸构件模型；当风速大于10 m/s时，D/L<0.2，波浪力模型应选择小尺寸构件模型。图12b为水深d1一定，浮桶直径D=8.12 m，10.12 m，12.12 m时，风速与D/L关系曲线图。除了风速的变化对D/L有显著影响以外，浮桶直径D的变化对D/L有直接影响。浮桶直径为8.12 m时，D/L=0.2的风速临界点约为10 m/s；浮桶直径为10.12 m时，D/L=0.2的风速临界点约为11 m/s；浮桶直径为12.12 m时，D/L=0.2的风速临界点约为12m/s。

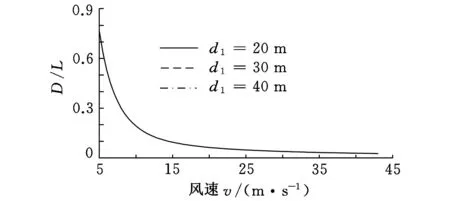
(a) 浮桶直径不变

(b) 水深不变图12　风速与D/L的关系

图13分别给出了浮桶直径不变和水深不变时波浪载荷波形。图13a给出了浮桶直径不变，水深d1=20m，30m，40m时，风速与波浪载荷关系二维曲线；图13b为对应的三维关系曲线图。从图13a可以看出，随着风速的增大，波浪力逐渐递增，但低风速时，风速的增大对波浪力影响较小，一定风速(临界点)以后，随着风速的增大，波浪力迅速上升。不同水深对应的风速临界点值不同，水深为20m、30m、40m时，临界点分别为5m/s、10m/s、12m/s。水越深，波浪力越小，因为随着水深d1的增大，函数1/coshd1减小。风速为43m/s，水深为20m、30m、40m时，波浪载荷分别为5.33MN、4.03MN、3.22MN(浮桶直径8.12m)。图13c给出了水深不变，浮桶直径分别为8.12m、10.12m、12.12m时，风速与波浪载荷关系二维曲线。图13d为对应的三维关系曲线图。可以看出，浮桶直径的变化对风速临界点的影响不大，风速临界点均在5m/s左右(水深20m)。随着风速的增加，不同的浮桶直径对波浪载荷上升的斜率影响很大，风速为43m/s，浮桶直径分别为8.12m、10.12m、12.12m时，对应的波浪载荷分别为12.5MN、8.5MN、5.33MN。

(a)浮桶直径不变二维图形

(b)浮桶直径不变三维图形

(c)水深不变二维图形

(d)水深不变三维图形图13　浮桶直径不变、水深不变时波浪载荷

图14给出了不同风速条件下的波浪载荷波形，可以得到水深、浮桶直径与波浪力之间的关系。从图14可以看出，在不同风速条件下得到的曲面形状类似，随着水深d1的增大，波浪力逐渐减小；随着浮桶直径D的增大，波浪力逐渐增大；风速越大，变化的速率就越大；随着风速的增大，波浪力增大；各曲面最大值均出现在水深d1取最小值，浮桶直径D取最大值的时候，分别为4.92MN·m、8.77MN·m、12.0MN·m、14.8MN·m。

(a)风速为15 m/s

(b)风速为20 m/s

(c)风速为25 m/s

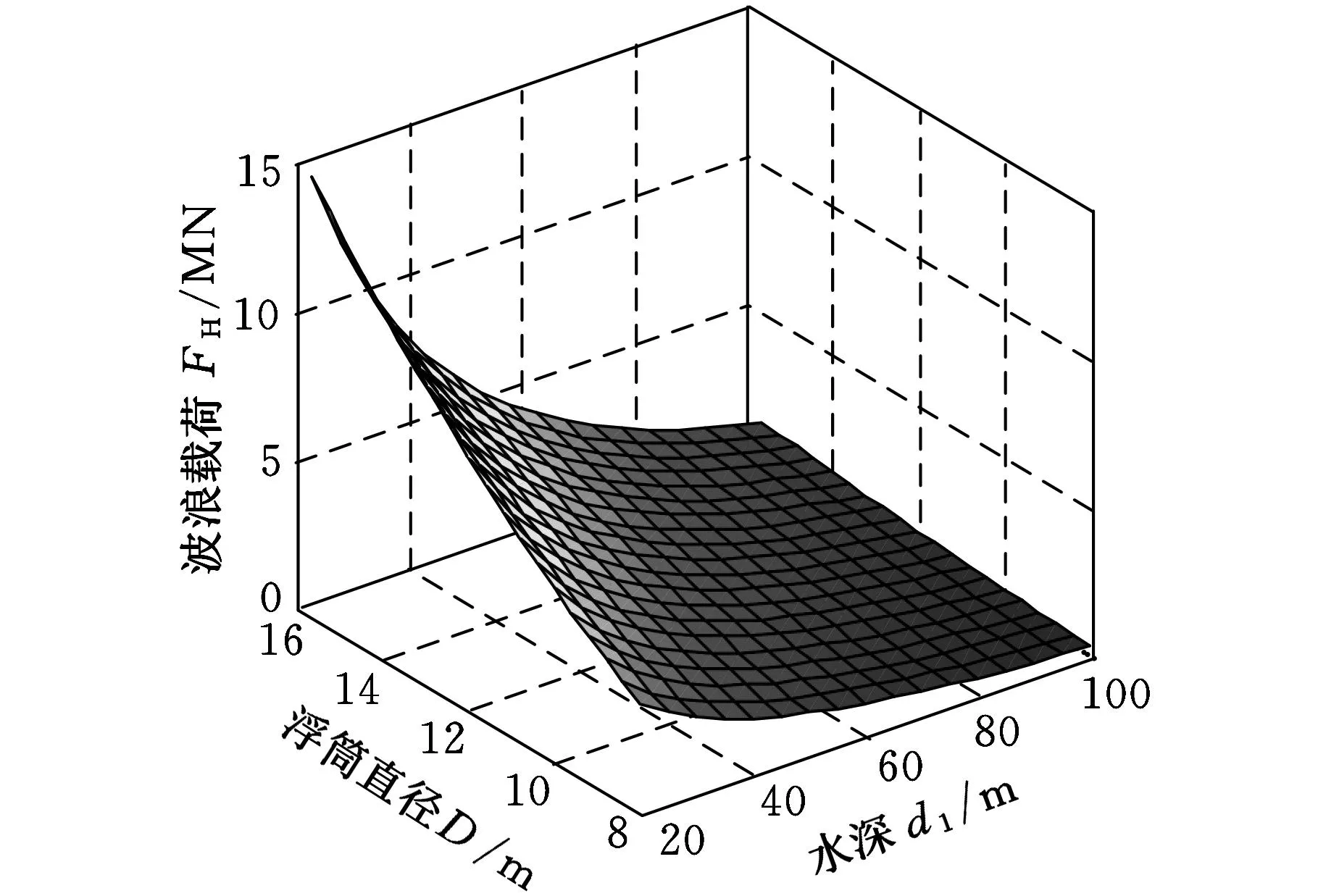
(d)风速为30 m/s图14　不同风速条件下波浪载荷

图15a为考虑风波联合作用，作用在浮桶1底部的力矩(风载荷与波浪载荷方向相同)。从图中可以看出，不同的工况下计算得到的力矩变化趋势明显不同。在风速小于4m/s时，风电机组处于启动状态，力矩接近于0；风速在4～10.5m/s时，风电机组处于最大风能跟踪的运行状态，力矩随着风速的增加而快速上升，在10.5m/s时，力矩约为28MN·m，这一阶段浮桶直径的变化对力矩的影响很小，因为此时风载荷产生的力矩比波浪载荷产生的力矩要大，所以浮桶直径变化对力矩产生的影响不明显；风速在10.5～25m/s时，风电机组处于变桨距限制风能捕获的状态，力矩有一个随风速增大而下降的过程，然后随着风速的增大而逐渐上升，浮桶直径变化对总力矩产生的影响逐渐显现。风速为25m/s时，力矩出现突变，这是因为风速在25m/s以下时，风载荷基于叶素-动量理论计算得到(风电机组正常运行)；风速在25m/s以上时，风载荷按停机顺桨状态估算公式得到；力矩随着风速的增大而增大，浮桶直径变化对力矩产生的影响较大，这一阶段风载荷相对波浪载荷对力矩的影响要小得多。风速为43m/s，浮桶直径为8.12m、10.12m、12.12m时，对应的漂浮平台底端力矩分别为46.66MN·m、66.81MN·m和91.49MN·m。

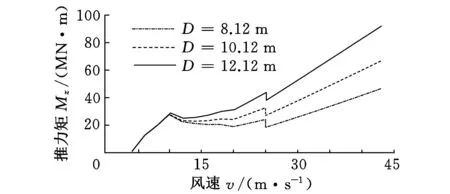
(a)风载荷与波浪载荷方向相同

(b)风载荷与波浪载荷方向相反图15　风速与漂浮平台底端力矩关系

图15b所示为考虑风波联合作用，作用在浮桶1底部的力矩(风载荷与波浪载荷方向相反)。从图15b可以看出，不同工况下计算得到的力矩变化趋势明显不同。风速小于4m/s时，风电机组处于启动状态，力矩接近于0。风速在0～20m/s时，风产生的推力矩大于波浪载荷力矩，浮桶直径变化对总力矩产生的影响逐渐显现。在风速大于20m/s后，波浪载荷力矩大于风的推力矩，随着风速的增大而增大，风速在43m/s，浮桶直径为8.12m，10.12m，12.12m时，对应的漂浮平台底端力矩分别为18.92MN·m、39.09MN·m、63.76MN·m。

5结论

(1)以海上大型漂浮式风电机组的三浮桶式支撑结构为研究对象，考虑风波联合作用，分别建立了风载荷和波浪载荷模型以及风波联合载荷模型，依据浮桶直径与波长的比值确定波浪力适用的计算模型，得到了不同工况、不同环境参数和结构参数条件下的载荷结果。

(2)随着风速的增大，波浪力逐渐递增，但低风时，风速的增大对波浪力影响较小；在达到风速临界点以后，随着风速的增大波浪力迅速上升。不同水深对应的风速临界点不同，浮桶直径的变化对风速临界点的影响不大。

(3)不同的工况下计算得到的浮桶底部总力矩变化趋势明显不同，风电机组处于启动状态时，力矩接近于0；处于最大风能跟踪运行状态时，力矩随着风速的增大而快速上升；处于变桨距限制风能捕获状态时，力矩有一个随风速增大而下降的过程，然后随着风速的增大而逐渐上升；停机顺桨后，力矩随着风速的增大而增大。

参考文献：

[1]MoriatyPJ,ButterfieldS.EffectofTurbulenceVariationonExtremeLoadsPredictionforWindTurbines[J].JournalofSolarEnergyEngineering, 2002, 124(4): 387-395.

[2]BuhlJrML,JonkmanJM,WrightAD,etal.FastUserGuide[R].NationRenwableEnergyLaboratory, 2002.

[3]KarimiradM,MoanT.ASimplifiedMethodforCoupledAnalysisofFloatingOffshoreWindTurbines[J].MarineStructures, 2012, 27(1): 45-63.

[4]HendersonAR,ZaaijerMB,CampTR.HydrodynamicLoadingonOffshoreWindTurbines[R].Delft:SectionWindEnergy,TechnicalUniversityofDelft,ReportSW-0218x, 2003.

[5]PeeringaJM.WaveLoadsonOffshoreWindTurbines[R].EnergieonderzoekCentrumNederland,ECN-C-04-042, 2004.

[6]徐建源, 祝贺. 风波联合作用海上风力机动态特性分析[J]. 中国电机工程学报, 2010,30(5): 120-124.

XuJianyuan,ZhuHe.DynamicCharacteristicAnalysisofOffshoreWindTurbineunderCombinedWindandWaveAction[J].ProceedingsoftheCSEE, 2010, 30(5): 120-124.

[7]陈小波, 李静, 陈建云. 基于流函数理论的近海风机非线性波浪载荷计算[J]. 湖南大学学报, 2011, 38(3): 22-28.

ChenXiaobo,LiJing,ChenJianyun.CalculationoftheNonlinearWaveForceofOffshoreWindTurbineBasedontheStreamFunctionWaveTheory[J].JournalofHunanUniversity, 2011, 38(3): 22-28.

[8]SeidelM,VonMutiusM,RixP,etal.IntegratedAnalysisofWindandWaveLoadingforComplexSupportStructuresofOffshoreWindTurbines[C]//ProceedingsoftheOffshoreWindConference,Copenhagen, 2005.[2015-01-01]http://xs.cytbj.com/scholar?q=Integrated+Analysis+of+Wind+and+Wave+Loading+for+Complex+Support+Structures+of+Offshore+Wind+Turbines.

[9]李德源, 刘胜祥, 张湘伟. 海上风力机塔架风波联合作用下的动力响应数值分析[J]. 机械工程学报, 2009, 45(12): 46-52.

LiDeyuan,LiuShengxiang,ZhangXiangwei.DynamicalResponseNumericalAnalysisoftheOffshoreWindTurbineTowerunderCombinedActionofWindandWave[J].JournalofMechanicalEngineering, 2009, 45(12): 46-52.

[10]PeeringaJM.WaveLoadsonOffshoreWindTurbines[R].Petten，NetherlandsEnergyResearchCentreoftheNetherlands, 2004,ECN-C-04-042.

[11]NeumannG,PiersonWJ.ADetailedComparisonofTheoreticalWaveSpectraandWaveForecastingMethods[J].DeutscheHydrografischeZeitschrift, 1957, 10(4):134-146.

[12]戴巨川. 叶片断裂事故条件下直驱式风电机组动态特性分析[J]. 机械工程学报, 2013, 49(2): 190-198.

DaiJuchuan.DynamicCharacteristicsAnalyzedofLargeScaleDirectly-drivenWindTurbinesunderBladeFractureAccidentCondition[J].JournalofMechanicalEngineering, 2013, 49(2):190-198.

[13]戴巨川, 胡燕平, 刘德顺, 等.MW级变桨距风电机组叶片转矩计算与特性分析[J]. 太阳能学报，2010，31(8)：1030-1036.

DaiJuchuan，HuYanping，LiuDeshun，etal.TorqueCalculationandCharacteristicsAnalysisofBladeforMWAdjustable-pitchWindTurbine[J].ActaEnergiaeSolarisSinica, 2010, 31(8): 1030-1036.

[14]Dai J C, Hu Y P, Liu D S, et al. Aerodynamic Loads Calculation and Analysis for Large Scale Wind Turbine based on Combining BEM Modified Theory with Dynamic Stall Model[J]. Renewable Energy, 2011, 36(3): 1095-1104.

[15]Zhang R, Tang Y, Hu J, et al. Dynamic Response in Frequency and Time Domains of a Floating Foundation for Offshore Wind Turbines[J]. Ocean Engineering, 2013, 60: 115-123.

[16]陈严, 蔡安民, 叶枝全, 等. 近海风力机在极限波浪作用下的初步计算分析[J]. 太阳能学报, 2008, 29(2): 180-186.

Chen Yan, Cai Anmin, Ye Zhiquan, et al. Primary Calculation and Analysis of the Offshore Wind Turbine under the Action of Extreme Wave [J]. Acta Energiae Solaris Sinica, 2008, 29(2): 180-186.

[17]刘胜祥, 李德源, 黄小华, 等. 风波联系作用下的风力机塔架疲劳特性分析[J]. 太阳能学报, 2009, 30(10): 1250-1256.

Liu Shengxiang, Li Deyuan, Huang Xiaohua, et al. Fatigue Characteristic Analysis of the Offshore Wind Turbine Tower under Combined Wind and Wave[J]. Acta Energiae Solaris Sinica, 2009, 30(10): 1250-1560.

[18]王树青, 梁丙臣. 海洋工程波浪力学[M]. 青岛: 中国海洋大学出版社, 2013.

(编辑张洋)

Calculation and Analysis of Wind and Wave Loads of Offshore Floating Wind Turbines

Liu Deshun1Liu Ziqi1Dai Juchuan1Long Xin2

1.Hunan University of Science and Technology，Xiangtan，Hunan，411201 2.State Key Laboratory of Offshore Wind Power Generation Technology and Detection，Xiangtan，Hunan，411102

Abstract:Three-floating-barrel support structure of large scale offshore floating wind turbines was researched herein. Considering the combined action of wind and wave, using the BEM theory and linear wave theory, the wind load model, wave load model, and wind-wave combination load model were built. In calculation process, different operating conditions of wind turbines were considered, the different wave load models,Morison formula and diffraction theory,were selected based on the ratio of floating barrel diameter to wave length. Load calculation results for different operating conditions, environment parameters and structure parameters were obtained, and the load characteristics were analyzed.

Key words:floating wind turbine; wind-wave load; blade element momentum(BEM) theory; linear wave theory

收稿日期：2015-01-13

基金项目：国家自然科学基金资助项目(51205123,51475160)；湖南省教育厅科研优秀青年资助项目(15B084)

中图分类号：TK83

DOI：10.3969/j.issn.1004-132X.2016.01.006

作者简介：刘德顺，男，1962年生。湖南科技大学机电工程学院教授、博士研究生导师。主要研究方向为机械动力学、风电技术与装备等。发表论文100余篇。刘子其，男，1988年生。湖南科技大学机电工程学院硕士研究生。戴巨川，男，1979年生。湖南科技大学机电工程学院副教授。龙辛，男，1962年生。海上风力发电技术与检测国家重点实验室高级工程师。