塔影效应简化模型试验

王　扬，李学敏，Dimitris Mathioulakis

(1.华中科技大学 中欧清洁与可再生能源学院，湖北 武汉 430074； 2.雅典国家技术大学 机械工程学院，希腊 雅典 999028)



塔影效应简化模型试验

王扬1，李学敏1，Dimitris Mathioulakis2

(1.华中科技大学 中欧清洁与可再生能源学院，湖北 武汉 430074； 2.雅典国家技术大学 机械工程学院，希腊 雅典 999028)

摘要：对塔影效应简化模型进行了试验研究，将上游叶轮简化为二维平板，下游塔架简化为二维圆柱，借助压力传感器及粒子图像测速技术，测量了8种平板位置下圆柱表面压力分布及干涉区域瞬态速度场数据，分析了圆柱表面压力、升力因数、阻力因数、干涉区域时均速度场及其相干特性。研究结果表明：靠近平板的圆柱一侧受平板影响较为明显，且随平板远离圆柱，圆柱表面压力因数与无平板时压力因数的相关系数自-0.37增至0.97，圆柱所受合力因数在原值(1.12)的72%与115%之间。

关键词：塔影效应；圆柱；压力分布；粒子图像测速技术

0引言

随着水平轴风力机大型化的发展，风力机的塔影效应成为一个不容忽视的问题。由于上游叶片尾迹改变了塔架的绕流状况，两者之间产生明显的干涉效应，由此导致的非定常流动使风力机输出功率呈现周期性变化，同时也对叶轮及塔架的结构动力学特征产生不良影响，并产生噪声辐射。

目前，国内外已经进行了一系列关于塔影效应的试验研究。文献[1]对风力机的输出功率进行了测量，证明了塔影效应导致风力机功率出现较大波动，并在叶片扫过塔架区域时最突出。文献[2]在低速风洞试验中，对一个两叶片下风型风力机的缩小模型进行了研究，通过采集到的叶片表面压力变化验证了塔影效应的影响。但这些研究均未涉及干涉区域的流动状态，由于风力机流动是一个非常复杂的三维非定常流动，为方便对干涉区域的研究，可将试验模型简化。在此方面，国外尚无已发表的成果，而国内的研究也较少。文献[3]建立了一个考虑上游风轮尾迹与下游塔架相互干涉的简化模型，即将上游叶片简化为一个二维叶栅，下游塔架简化为一个圆柱，基于Navier-Stokes方程，分析了两者相互干涉下的物理特性，包括旋涡脱落频率、升阻力的脉动与频谱以及纵向位置对以上物理特性的影响。但该研究并未获得流场的试验数据，不便更直观地研究这一流动现象。

本文借助粒子成像测速(particle image velocimetry，PIV)技术研究了上游平板与下游圆柱干涉区域的流动形态，并测量了下游圆柱表面的压力分布。并且对上游平板在不同位置时，下游圆柱绕流的动力学特性、表面压力和升阻力因数进行了研究。

1试验设备及方法

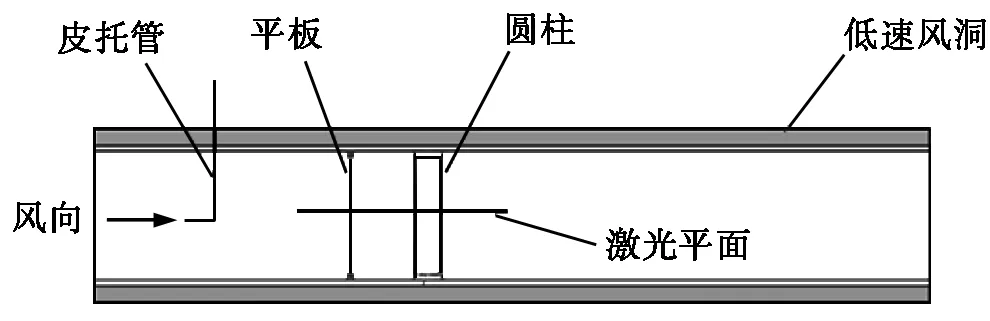
图1　试验装置布置示意图

试验所用的装置布置如图1所示。低速风洞试验段长度为1 m，横截面为0.23 m×0.40 m，来流风速U∞=8.5 m/s，湍流强度为0.5%。简化试验模型几何尺寸参考DTU 10 MW RWT型风力机，风力机几何尺寸中，46 m高度截面处的塔筒直径为7.186 m，叶片距离塔筒轴线距离为16.71 m。试验圆柱直径D为0.06 m，长度L为0.23 m，长径比Ra=3.83，垂直布置于风洞试验段中间轴风洞出口上游 0.9 m处。圆柱可绕自身轴线旋转，阻塞率Rb=15%。两道沟槽分别水平布置于风洞试验段上下表面，位于圆柱轴线上游L=0.14 m处。平板模型宽0.055 m，厚度为0.003 m，上下两端分别固定于两侧沟槽中，可沿沟槽滑行以调整平板与圆柱的相对位置。试验模型中L/D比值与风力机对应几何尺寸比值保持一致。

试验借助2D PIV系统(TSI.Inc公司)对测量域内流场的两个速度分量u(顺来流方向)及v(垂直于壁面方向)进行测量，试验用高速相机(型号POWER VIEW 4MP, TSI.Inc公司)的分辨率为1 376 Pixel×1 024 Pixel，与文献[4]一致。激光光源从模型侧方照明流场，并与压力测试孔所在平面重合。试验圆柱由亚克力制成，激光强度足以照亮圆柱背面流场。测量域大小为3.00D×2.25D，圆柱圆心设为坐标原点，h为平板下沿到风洞中间轴的距离，如图2所示。

图2　测量域示意图

试验采用压差传感器(NSC 250LD)测量圆柱表面的压力分布，压差传感器的通道1通过一根长0.25 m的细塑料管与圆柱壁面上的通孔相连，通道2暴露在大气环境中，以此获得圆柱表面方位角θ处的压强值Pθ与大气压强P0的差值△P所对应的电信号，传感器量程为-250～250 Pa，精确度为0.25%。来流静压及动压通过一个布置在平板上游0.2 m处的皮托管测得。

试验选取平板相对于圆柱的8个位置，即6h/D=0，1，2，…，7(为使比值取整，使用6h/D而非h/D)，分别测量了其干涉区域流场及圆柱表面压力分布。通过PIV系统连续采集了每个位置下的300幅时间序列的瞬态速度场图片，采集速率为5帧/s，总采集时间为60 s。通过压差传感器采集了每个位置下圆柱表面一周(剧变区域步长为5°，缓变区域步长为10°)的压力分布，采样频率为1 000 Hz，采样时间为30 s，在一些高度湍流区域，采样时间延长为60 s。

为描述圆柱表面压力分布，压力因数Cp可依据来流的静压P∞及动压Pdynamic计算得出：

(1)

其中：Pθ为圆柱表面方位角θ处的压强值。

依据文献[5]，升力因数Cl及阻力因数Cd可按照下式计算：

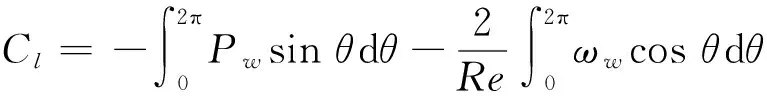
(2)

(3)

其中：Pw及ωw分别为圆柱表面θ处的无量纲压力及涡量。依据文献[6]，在Re=104～2×105时，随着流动分离的加剧，周期性涡街转变为湍流，此时升阻力主要由圆柱表面压差决定，阻力因数也趋于稳定。因而本试验在Re=27 500情况下，ωw对升阻力的影响可以忽略，Cl及Cd计算公式可由圆柱表面压力积分得来：

(4)

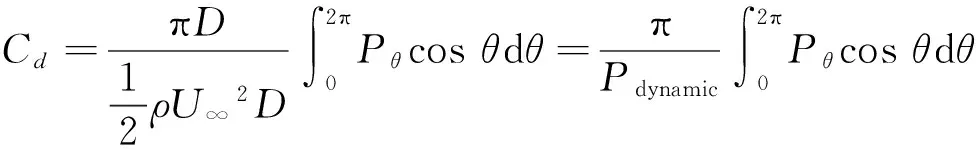
(5)

2试验结果与分析

2.1圆柱表面压力分布

为检测试验设备，对未添加平板的圆柱绕流进行了验证试验(Re=27 500,Ra=3.83,Rb=15.0%)。验证试验压力因数分布与文献[7](Re=30 000,Ra=6,Rb=15.2%)光滑圆柱绕流试验结果对比如图3所示。

由图3可知：验证试验结果与文献[7]的变化趋势、极值点、前驻点及流动分离点吻合较好。验证试验压力因数Cp曲线的极值分别出现在θ=0°(前驻点)及θ=65°处，两者压力因数幅值差约为2.5。在流动分离区域，即θ=85°与θ=275°之间，Cp保持在较低数值，由于验证试验中Ra更小，该区域Cp值略大于参考文献值。验证试验Cd计算结果为1.126，与文献[7]的结果(1.14)吻合较好，由于圆柱绕流的对称性，Cl在 0附近波动。

图4为平板相对于圆柱8个位置时，圆柱表面压力因数Cp的分布曲线。由图4可知：当6h/D=0时，前驻点移至θ=320°处，压力因数在θ=20°处达到最小值，经过较小波动后，自θ=40°处迅速上升，直到θ=150°处趋于平稳，在θ=260°处达到圆柱下侧流动分离点后快速升至前驻点，随后快速下降至最低点。

当6h/D=1时，前驻点移至θ=330°处，压力因数Cp在θ=40°处达到最小值；经历两次较大波动后自θ=100°处稳步上升；在θ=180°处，压力因数出现一个明显的上升，由0.95跃至1.13并保持平稳直至抵达圆柱下侧流动分离点θ=260°处。

图3 验证试验压力因数曲线与文献[7]结果对比 图4 不同平板位置圆柱表面压力因数曲线对比

当6h/D=2时，前驻点移至θ=335°处，压力因数曲线在最小值(θ=20°处)后保持相对稳定，在θ=60°及θ=180°处经历两次跳跃后稳定在0.41，直至在θ=270°处抵达圆柱下侧流动分离点。

对于6h/D=3,4,5,6时，前驻点进一步向θ=0°处(6h/D=6时达到θ=0°)移动，压力因数曲线在经过圆柱上侧流动分离点后保持在较低水平(0.2～0.4)，并在θ=180°处上升并保持稳定，在θ=270°处抵达圆柱下侧流动分离点。

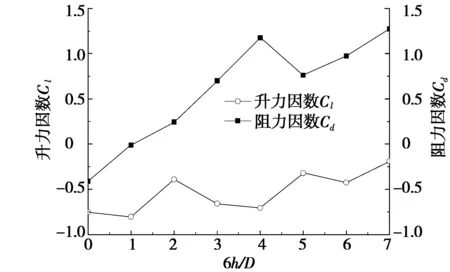
图5　圆柱阻力因数及升力因数随平板位置变化曲线

当6h/D=7时，前驻点停留在θ=0°处，在经过圆柱上侧流动分离点θ=80°后，压力因数曲线稳定在0.55，在θ=210°处曲线下降并稳定在0.45(θ=220°处)，在θ=270°处抵达圆柱下侧流动分离点。

图5为圆柱阻力因数Cd及升力因数Cl随6h/D的变化曲线，Cd及Cl的方向定义见图2。随着平板沿垂直于壁面方向远离圆柱，圆柱阻力因数Cd自-0.41上升至峰值1.17(6h/D=4)，再降至0.76(6h/D=5)后又回升至1.27；圆柱升力因数Cl则在波动中逐渐由-0.75增加至-0.19;圆柱阻力因数Cd及升力因数Cl均分别回归于验证试验中所测得的Cd及Cl值。

2.2干涉流域

图6为4种平板位置下干涉区域的时均流线图。由图6可知：圆柱下侧主要受到平板剪切层的影响。在平板位置6h/D=0时，由于圆柱的阻碍作用，圆柱表面0°<θ<60°区域附近出现一个较大范围的逆时针涡旋结构，由此导致该区域Cp曲线剧烈波动；之后随着平板位置上移，平板剪切层对圆柱上侧作用增加，在6h/D=3时，圆柱上侧受到尾迹及剪切层的双重影响；而在6h/D=6及之后，圆柱整体浸没于平板剪切层中，不再受到平板尾迹区影响。

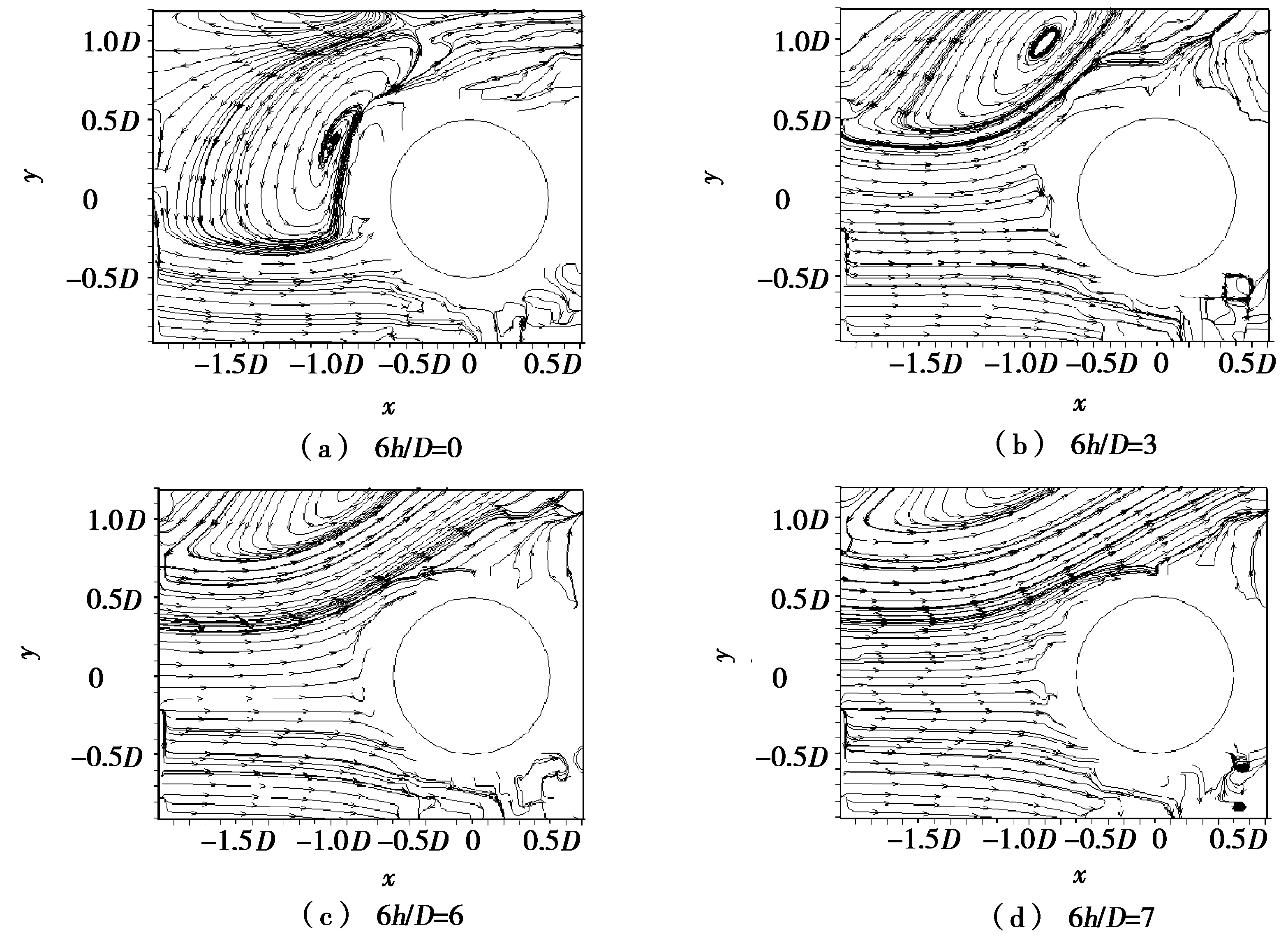
图6　不同平板位置下干涉区域的时均流线图

2.3相干特性分析

为更清楚地研究不同压力分布曲线之间的形状及幅值差异，可引入相关系数CC及幅值率AR。其中，CC为不同平板位置下压力因数分布曲线与验证试验压力因数分布曲线的相关系数，计算公式依据文献[8]：

(6)

(7)

CC或AR值越接近于1，该压力因数曲线的形状或极值越接近于验证试验曲线。

图7为相关系数CC及幅值率AR随平板位置的变化。由图7可知：AR值在0.6～1.5变化，并在6h/D=4时达到最大值1.46；CC值则由-0.37上升至0.97，在6h/D=5,6,7时，CC值均大于0.9，压力分布曲线与验证试验高度相关，表明平板对圆柱的干涉作用大幅度减弱。

图7　相关系数和幅值率随平板位置的变化

表1为不同平板位置下圆柱表面流动及所受合力。结合图7和表1可知：在6h/D=0,1,2时，圆柱表面0°<θ<80°区域附着的边界层被破坏，使圆柱上侧流动分离点前移，并将前驻点推至圆柱下侧，其相关系数CC均小于0.5，处于低相关性区间；在6h/D=3时，圆柱上侧流动分离点及前驻点逐渐回归其原位，其压力因数曲线与验证试验曲线处于中等相关性区间；而在6h/D=4,5,6,7时，由于平板尾迹对圆柱影响大幅减弱，圆柱上侧流动分离点及前驻点回归其原位，相关系数CC由0.87增至0.97，处于高相关性区间。随着平板沿垂直于壁面方向远离圆柱，前驻点自最大漂移点θ=320°逐渐靠近θ=0°(验证试验前驻点)，并在6h/D=6时回归θ=0°并保持，其移动范围为40°；两侧流动分离点表现出后移趋势，其中，圆柱上侧流动分离点自θ=30°逐步后移至θ=80°并保持，移动范围为50°，而圆柱下侧流动分离点自θ=260°(6h/D=1,2)移至θ=270°(6h/D=3,4,5,6,7)，移动范围为10°。

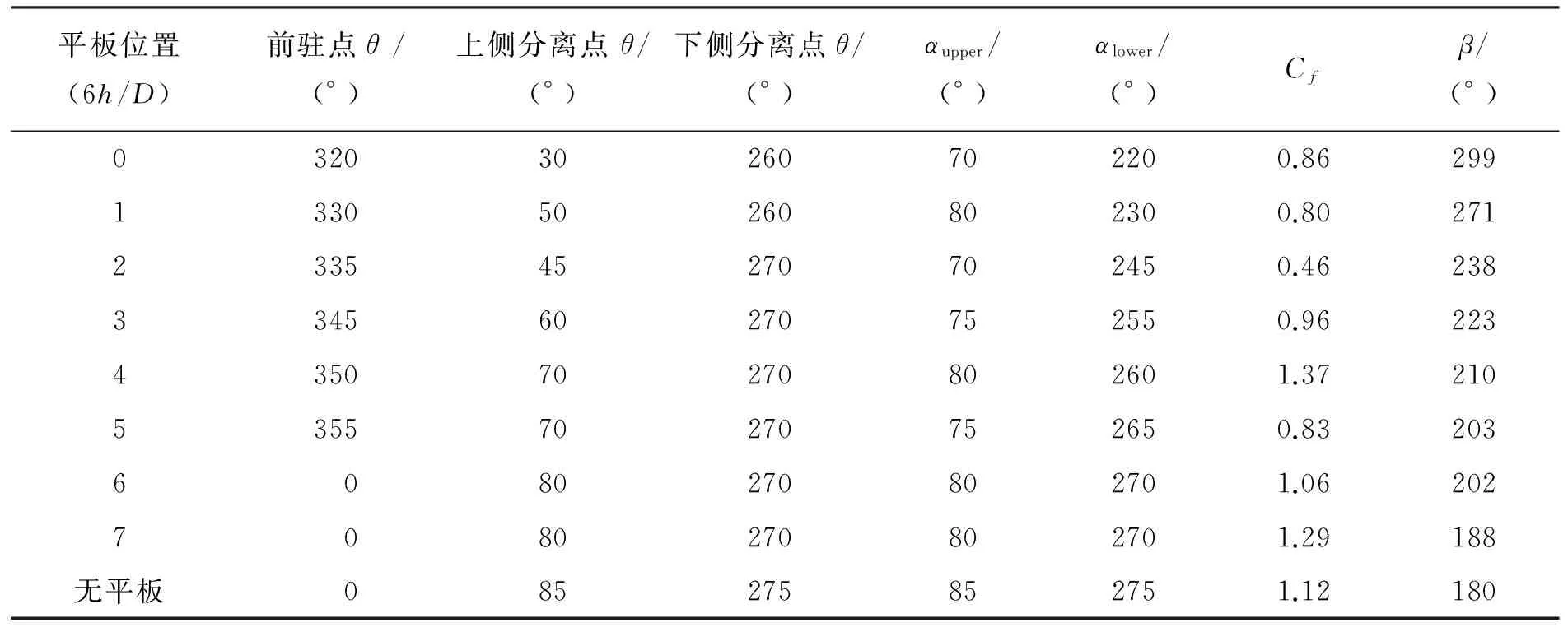
表1　不同平板位置下圆柱表面流动及所受合力

对8种平板位置，前驻点与圆柱上侧流动分离点之间的距离αupper均保持在70°与80°之间，接近于验证试验的85°。这表明随着平板剪切层对圆柱上侧的影响逐步增强，圆柱上侧的边界层重新附着于圆柱表面，圆柱上侧流动分离点及前驻点均被逐步拖拽回其原位，在整个过程中αupper保持相对稳定。而αlower，即前驻点与圆柱下侧流动分离点之间的距离，则随平板远离圆柱不断增大，这是由于圆柱下侧区域处流动相对稳定，使得下侧分离点稳定在θ=260°及θ=270°，趋近验证试验的θ=275°。

(8)

由表1可知:与验证试验中圆柱合力因数Cf=1.12相比，6h/D=0,1,2时的Cf有明显的下降，尤其是在6h/D=3时，Cf锐降至0.46；而随着6h/D=4,5,6,7中Cd值逐步回升，圆柱合力因数Cf也在波动中上升。Cf最小值为0.46,最大值为1.37,可见圆柱所受合力因数在原值(1.12)的72%至115%之间波动。整个过程中β沿逆时针方向从299°回归至188°，接近于验证试验的180°。可见随着平板移动，合力的幅值及方向均有明显变化，对于实际风力机来讲，当叶片扫过塔架时，塔架受到周期性变化的作用力，加剧塔架的受迫振动。

3结论

随着平板远离圆柱，两者的干涉作用迅速减弱。在此过程中，前驻点及圆柱上下侧流动分离点逐步自最远偏移点回归至原位，其中前驻点与圆柱上侧流动分离点偏移量较大，分别为40°及50°，而圆柱下侧流动分离点偏移量为10°。

随着平板远离圆柱，圆柱表面压力因数曲线与无平板时压力因数曲线的相关系数自-0.37增至0.97。圆柱所受合力因数在原值(1.12)的72%～115%波动，其方向自最远偏移点θ=299°逐步回归至θ=188°。

参考文献：

[1]MCSWIGGAN D,LITTLER T,MORROW D J,et al.A study of tower shadow effect on fixed-speed wind turbines[C].University Power Engineering Conference.2008:1-5.

[2]MUNDUATE X,COTON F N,GALBRAITH R A M.An investigation of the aerodynamic response of a wind turbine blade to tower shadow[J].Journal of solar energy engineering,2004,126(4):1034-1040.

[3]曹人靖,胡骏.水平轴风力机风轮尾迹与圆柱型塔架的相互干涉[J].太阳能学报,2006(4):326-330.

[4]LAPIRIS P G,MATHIOULAKIS D S.Experimental study of vortical structures in a periodically perturbedow over a backward-facing step[J].International journal of heat and fluid flow,2014(47):101-112.

[6]NARASIMHAMURTHY V D,ANDERSSON H I.Numerical simulation of the turbulent wake behind a normalat plate[J].International journal of heat and fluid flow,2009(30):1037-1043.

[7]WEST G S,APELT C J.The effects of tunnel blockage and aspect ratio on the meanow past a circular cylinder with Reynolds numbers between 104 and 105[J].Fluid mech,1982(114):361-377.

[8]WU B,YIN Y T.Mean pressure distributions around a circular cylinder in the branch of a T-junction with/without vanes[J].Applied thermal engineering,2014(88):1-12.

[9]NAJJAR F M,VANKA S P.Effects of intrinsic three-dimensionality on the drag characteristics of a normalat plate[J].Physics of fluids,1995(7):2516-2518.

[10]NARASIMHAMURTHY V D,ANDERSSON H I.Numerical simulation of the turbulent wake behind a normalat plate[J].International journal of heat and fluid flow,2009(30):1037-1043.

基金项目：湖北省自然科学基金项目(2015CFB628);华中科技大学自主创新基金项目(2015TS035)

作者简介：王扬(1990-),男,河南洛阳人,硕士生;李学敏(1977-),男,湖北武汉人,副教授,博士,硕士生导师，主要研究方向为流体机械内流分析、气动声学和风能利用技术等.

收稿日期：2016-01-26

文章编号：1672-6871(2016)04-0026-06

DOI:10.15926/j.cnki.issn1672-6871.2016.04.006

中图分类号：TK83

文献标志码：A