一题多变的深入探究

北京一零一中学 廖会平

本文先按代数方法求解，再根据代数方法求得的解探讨几何计算方法，加入D点位置变化和ACB大小变化两种情况进行探究，层层递进。首先从探究特殊情况下三条线段之间的关系入手，再逐渐从两个方面改变已知量加深探究，最后得出D点位置变化和ACB大小变化的紧密关系：

探究1.1：已知等腰直角三角形ABC，∠C=900，在斜边AB的同侧作角∠ADB=900，连接CD，试探讨：线段CD,AD,BD之间的数量关系？

解：几何方法: 在AD上取AE，使得AE=BD,连接CE,则

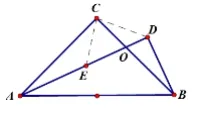
在斜边AB的同侧作角∠ADB=900，此时也有两种情况，一是在C点的右侧，二是在C点的左侧。第一种情况已解决，但是在C点的左侧情况类似于第一种情况，就在此不做探究，其关系是。再深一层，如D点跟C点在直线AB的异侧呢？下面对这种情况继续探究。

探究1.2：已知等腰直角三角形ABC，∠C=900，在斜边AB的异侧作角∠ADB=900，连接CD，试探讨：线段CD,AD,BD之间的数量关系？

解：几何方法:延长DA到E，使得AE=BD, 连接CE, 则

在斜边AB的同侧作角∠ADB=900，此时ADB的大小发生变化呢？线段CD,AD,BD之间的数量关系又会如何呢，下面先研究特殊角下的情形，比如600，下面对这种情况继续探究。

探究2.1：已知等腰三角形ABC，∠C=600，在斜边AB的同侧作角∠ADB=600，连接CD，试探讨：线段CD,AD,BD之间的数量关系？

解：几何方法: 在AD上取AE，使得AE=BD,连接CE,则

在斜边AB的异侧作角∠ADB=600，此时ADB的大小发生变化呢？线段CD,AD,BD之间的数量关系又会如何呢，下面对这种情况继续探究。

探究2.2：已知等腰三角形ABC，∠C=600，在斜边AB的异侧作角∠ADB=600，连接CD，试探讨：线段CD,AD,BD之间的数量关系？

解：几何方法: 延长DA到E，使得AE=BD,连接CE,则

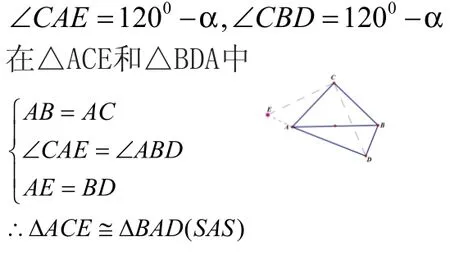
CE=AD ,∠E=∠BDA=600

设AD=x, AE=y,

在△DCE中由余弦定理有

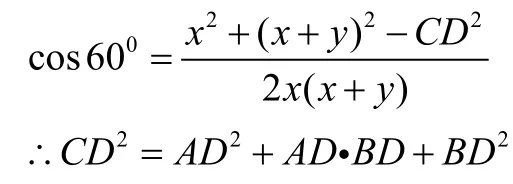
在斜边AB的同侧作角∠ADB=x0，此时∠ADB的大小发生变化呢？线段CD,AD,BD之间的数量关系又会如何呢，下面对这种情况继续探究。

探究3.1：已知等腰三角形ABC，∠C=x0，在斜边AB的同侧作角∠ADB=x0，连接CD，试探讨：线段CD,AD,BD之间的数量关系？

解：几何方法: 在AD上取AE，使得AE=BD,连接CE,则

在△ACE和△BDC中

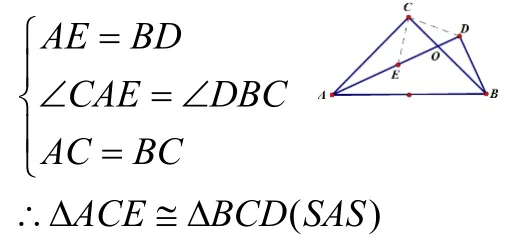
CE=CD ,∠ACE=∠BCD

∴∠ECD=∠ACB=x0,△DCE为等腰三角形.

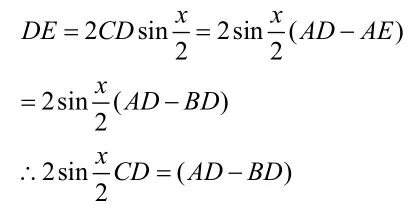
此问题的结论满足前面的特殊情况下的探究,具有一般性。

在斜边AB的异侧作角∠ADB=x0，此时ADB的大小发生变化呢？线段CD,AD,BD之间的数量关系又会如何呢，下面对这种情况探究。

探究3.2：已知等腰三角形ABC，∠C=x0，在斜边A B的异侧作角∠ADB=x0，连接CD，试探讨：线段CD,AD,BD之间的数量关系？

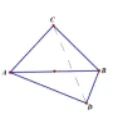
此种情况下，A,B,C,D这四点再不具有共圆的性质，且角之间的关系也被破坏，因此不再具有前面的关系,破坏了一般性.

本文主要结合代数和几何地解决几何问题,从代数中寻找解决几何方法,这也是一种解决几何的途径,为学生学习几何又提供了一种思路,同时又从数量关系和位置关系对这种问题进行变形,指引着学生对问题的进一步思考,也指明了思考的方向.