从Zygmund空间到Bloch型空间二阶加权微分复合算子的性质

彭明用，杨丛丽

(贵州师范大学 数学与计算机科学学院，贵州 贵阳　550001)

从Zygmund空间到Bloch型空间二阶加权微分复合算子的性质

彭明用，杨丛丽*

(贵州师范大学 数学与计算机科学学院，贵州 贵阳550001)

摘要：主要讨论了从Zygmund空间到Bloch型空间二阶加权微分复合算子的有界性与紧性，得到了相应的等价条件。

关键词：Zygmund空间；Bloch型空间；二阶加权微分复合算子；有界性；紧性

0引言

我们记Δ为复平面上的单位开圆盘，H(Δ)为Δ上解析函数的全体，对φ，φ∈H(Δ)且φ(Δ)⊆Δ，定义以φ，φ为符号的二阶加权微分复合算子为：φCφD2f=φf″(φ)， 其中f∈H(Δ)。

对f∈H(Δ)，Δ上Bloch空间和α-Bloch空间的定义分别为：

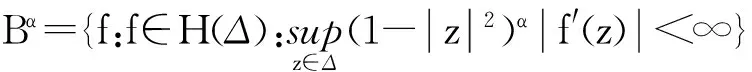
文献[2]在泛数

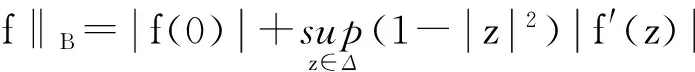
(1)

与文献[3]在范数

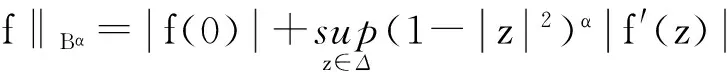
下它们都是Banach 空间。

小Bloch空间与小α-Bloch空间的定义如下：

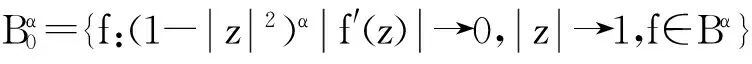
对f∈H(Δ)，Δ上μ-Bloch空间是指：

对f∈H(Δ)，Δ上的Zygmund空间是指：

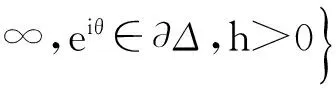
由文献[6]中的定理5.3可知：

(2)

在文献[7]中对任意的f∈Z有

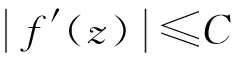
(3)

对任意f∈B在文献[8]有

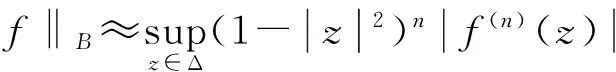
(4)

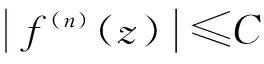
1主要结果及证明

引理1设φ，φ∈H(Δ)且φ(Δ)⊆Δ，μ是正规函数，那么φCφD2：Z(或Z0)→Bμ是紧的充分必要条件是φCφD2:Z(或Z0)→Bμ有界，对Z(或Z0)中的任意有界序列{fk}k∈N在Δ上内闭一致收敛于0(k→∞)，且‖φCφD2fk‖Bμ→0(k→∞)。

引理1的证明方法和文献[1]中的命题3.11的一样，故略去不证。

定理1设φ，φ∈H(Δ)且φ(Δ)⊆Δ，μ是正规函数，那么以下3个条件等价 :

①φCφD2:Z→Bμ有界；②φCφD2:Z0→Bμ有界；

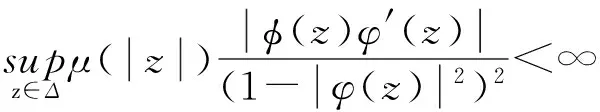
证明：①⟹②，显然。

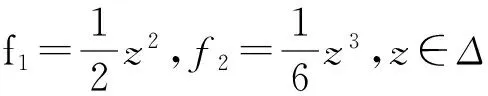
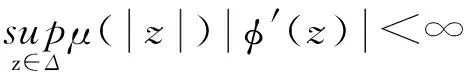
(5)

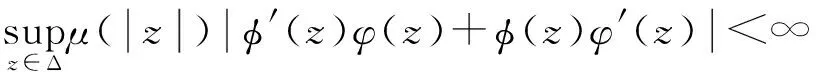
(6)

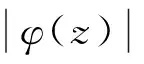
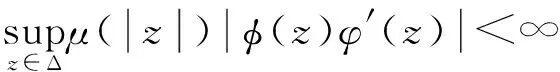
(7)

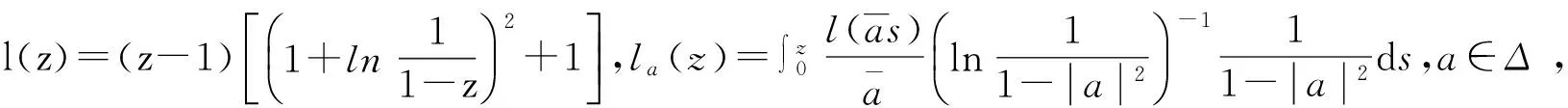
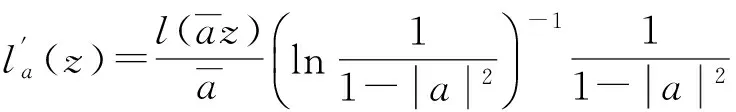
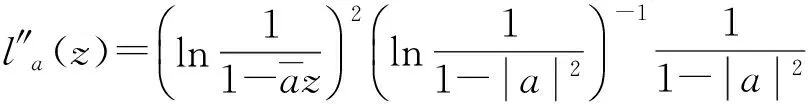
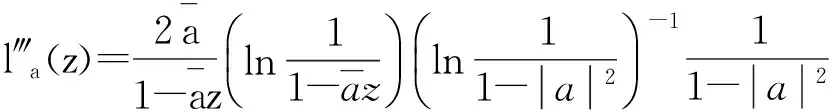
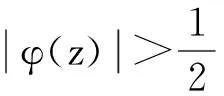
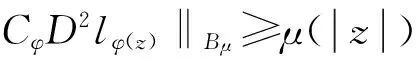
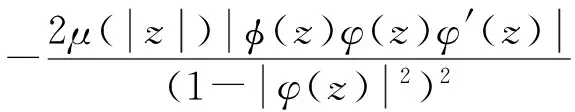
那么

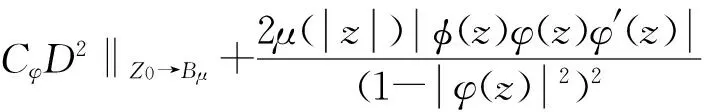
(8)

当a∈Δ〗{0}时，设

那么fa(z)∈Z0，从而

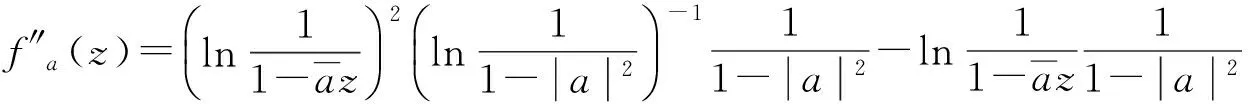
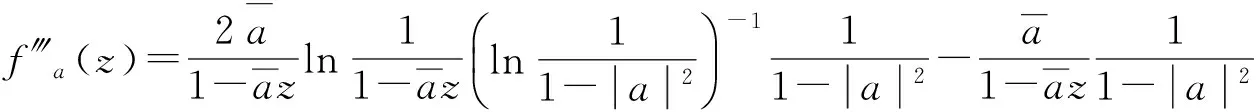
(9)

由(8)与(9)可知：

≤C‖φCφD2‖Z0→Bμ<∞

由(5)可知：

C‖φCφD2‖Z0→Bμ<∞

由(7)可知：

故③成立。

③⟹① 对任意的f∈Z，结合③可知：

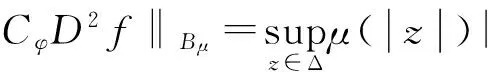
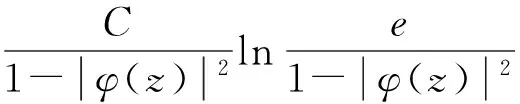
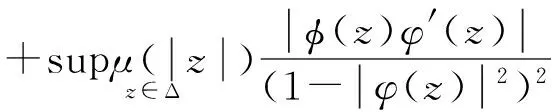
证毕。

定理2设φ，φ∈H(Δ)且φ(Δ)⊆Δ，μ是正规函数，那么以下3个条件等价 ： ①φCφD2:Z→Bμ紧 ；②φCφD2:Z0→Bμ紧；

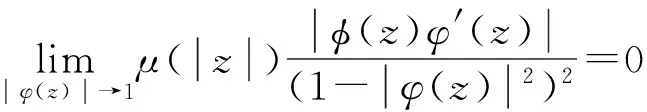
证明①⟹②，显然。

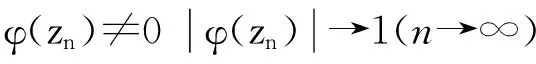
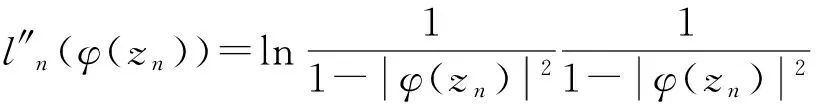
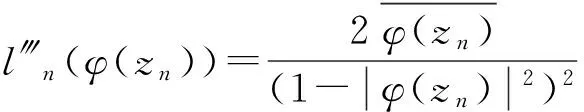
结合定理1的证明过程有：

‖φCφD2ln‖Bμ≥|μ(|zn|)|φ′(zn)l″(φ(zn))|-μ(|zn|)|φ(zn)φ′(zn)l‴n(φ(zn))||

则

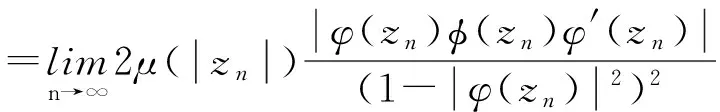
即我们所求的两个极限存在。

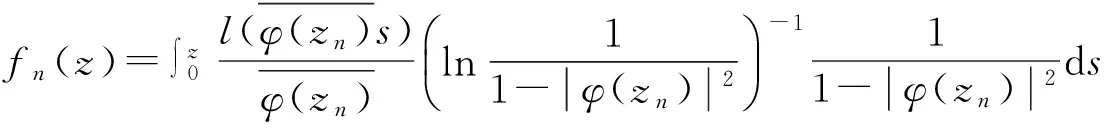
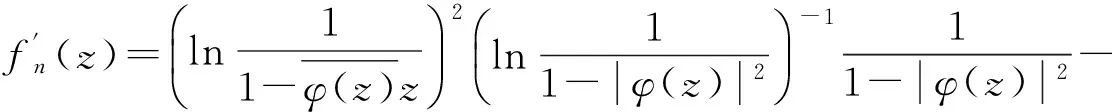
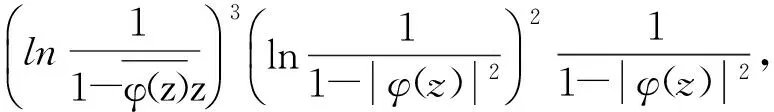
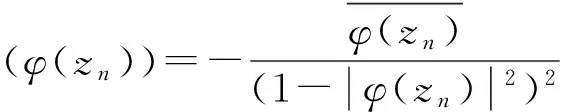
因为φCφD2:Z0→Bμ是紧的，由引理1可知：

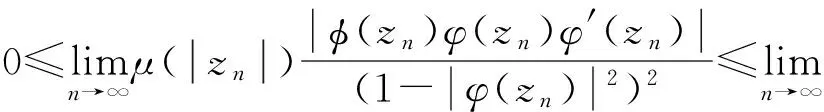
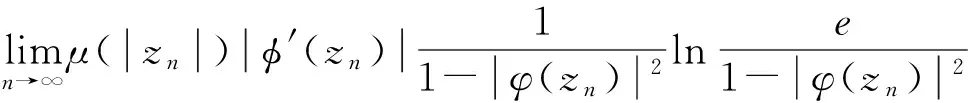
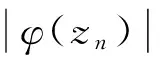
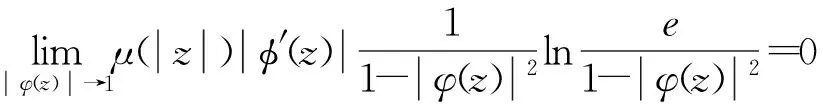
③⟹①，因为φCφD2:Z→Bμ有界，由定理1可知：

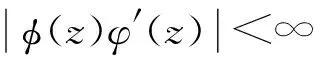
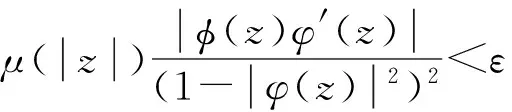
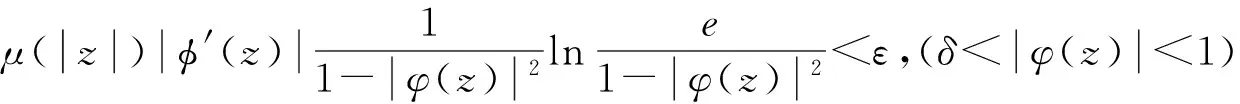
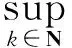
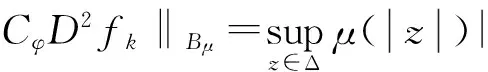
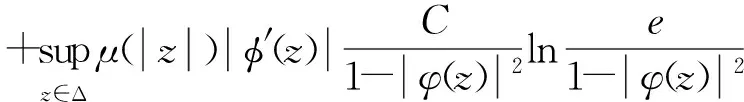
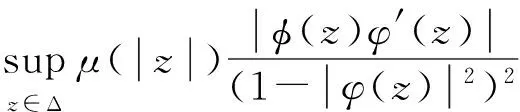
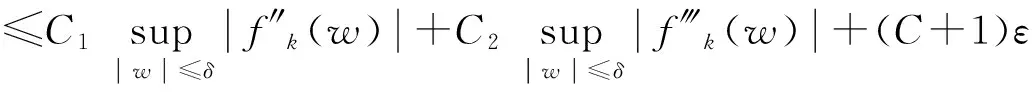
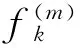
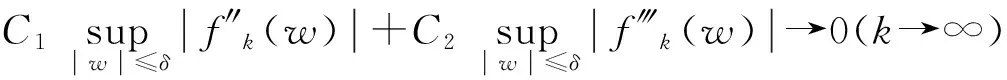
由引理1可知φCφD2:Z→Bμ紧。

证毕。

参考文献：

[1]COWENC,MACCLUERB.CompositionOperatorsonSpaceofAnalyticFunction[M].BocaRaton:CRCpress,1995.

[2]ANDERSONJ,CLAUNIEJ.POMMERENKECh.OntheBlochfunctionsandnormalfunctions[J].ReineAngewMath,1974,270:12-37.

[3]LIS,HASIWulan.Characterizationsofα-Blochspacesontheunitball[J].MathAnalAppl,2008,343(1):58-63.

[4]STEVICS.Bloch-typefunctionswithHadamardgaps[J].ApplMathcomput,2009,208:416-422.

[5]SHIELA,WILLIAMSD.Bondedprojections,duality,andmultipliersinspacesofanalyticfunctions[J].TransAmMathSoc,1971,162:287-302.

[6]DURENP.TheoryofHpspaces[M].NewYork:Academicpress,1970.

[7]LONGJR,QIUCH,WUPC.WeightedcompositionfollowedandproceededbydifferentiationoperatorfromZygmundspacestoBloch-type[J].InequalAppl,2014:152:40-47.

[8]WUYT,HASIWL.N:ProductsofdifferentiationandcompositionoperatorsOntheBlochspace[J].Math,2012,63:93-107.

The character of 2-th weighted composition followed and proceeded by differentiation operator from Zygmund spaces to Bloch-type spaces

PENG Mingyong,YANG Congli*

(School of Mathematical and Computer Science, Guizhou Normal University, Guiyang, Guizhou 550001,china)

Abstract:This paper mainly discussed the compactness and boundedness of 2-th weighted composition followed and proceeded by differentiation operator from zygmund spaces to Bloch-type spaces ,we obtain corresponding equivalent conditions.

Key words:Zygmund spaces;Bloch-type spaces;2-th weighted composition followed and proceeded by differentiation operator;boundedness; compactness

文章编号：1004—5570(2016)02-0056-04

收稿日期：2015-07-25

作者简介：彭明用(1989-)，男，硕士研究生，研究方向：函数论，E-mail:pmyonng18@163.com. *通讯作者：杨丛丽(1981-)，女，博士，副教授，硕士研究生导师，研究方向：函数论，E-mail:yangcongli@gznu.edu.cn.

中图分类号：O174

文献标识码：A