关于可逼近性和弱紧性的一个注记

罗正华,周 巍,陈丽珍

(华侨大学数学科学学院,福建 泉州 362021)

1 主要结果

设(X,‖·‖)是Banach空间.对于x∈X,C⊂X,d(x,C)=inf{‖x-y‖:y∈C}表示x到C的距离;PC(x)={z∈C:‖x-z‖=d(x,C)}表示C在x处的度量投影.如果对每个x∈X,PC(x)≠Ø,就称C是可逼近的(proximinal).显然可逼近集是闭的.

定理1 设X是Banach空间,C⊂X是有界闭凸集,则C是弱紧的当且仅当对于X上的每个等价范数|·|,C在(X,|·|)中均是可逼近的.

2 定理的证明

下述引理1可见文献[8],为了完整起见,我们给出证明.

引理1 设(X,‖·‖)是赋范线性空间,C为X的非空子集,则C是可逼近的当且仅当对每个r≥0,C+rBX均是闭的.

证明必要性.设C是可逼近的，当r=0时,C+0·BX=C是闭的.

当r>0时,设cn+bn→x,其中{cn}⊂C,{bn}⊂rBX，则d(cn+bn,C)→d(x,C),并且

d(cn+bn,C)≤‖cn+bn-cn‖=

‖bn‖≤r,∀n∈N.

因此d(x,C)≤r.取y∈PC(x)，则‖x-y‖=d(x,C)≤r,即x-y∈rBX，因而x=y+(x-y)∈C+rBX，所以C+rBX是闭的.

充分性.设每个r≥0,C+rBX均是闭的.特别地,取r=0时可知,C是闭的.

令x∈XC,记r=d(x,C)>0.取{xn}⊂C,使得

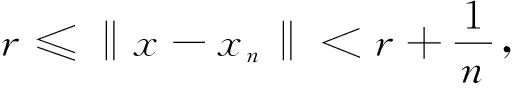
对每个n,令

则{yn}⊂rBX,并且

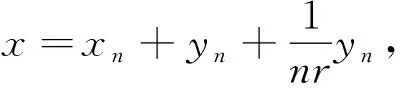
因此存在y∈C,z∈rBX,使得x=y+z.注意到

r=d(x,C)≤‖x-y‖=‖z‖≤r,

即‖x-y‖=d(x,C)，因而y∈PC(x)，所以C是可逼近的.引理证毕.

我们还需下述引理.

引理2 设X是Banach空间,C⊂X为有界闭凸集,则C是弱紧的当且仅当对每个内点非空的有界闭凸均衡集D⊂X,都有C+D是闭集.

证明必要性.设C是弱紧的,D是X的有界闭凸均衡子集,满足int(D)≠Ø，则C+D是弱闭的.再由C+D的凸性可知,C+D是闭的.

H-1={x∈X:f(x)=-1},H[-1,1]=

{x∈X:-1≤f(x)≤1}.

容易看到,C∩H[-1,1]=Ø.取{xn}⊂C,满足:f(xn)→-1.令

则

{yn}⊂H-1⊂H[-1,1],

并且

接下来,我们取一个开球U⊂H[-1,1],同时令

则D是有界闭凸均衡集,并且int(D)≠Ø.由

{xn}⊂C,{yn}⊂D,‖xn-yn‖→0，

可知

注意到

D⊂H[-1,1],C∩D=Ø,

则0∉C-D=C+D.这意味着,C+D不是闭的.产生矛盾.引理证毕.

利用引理1,2,下面我们完成定理1的证明.

定理1的证明必要性.设C是弱紧的,|·|是X上的等价范数，则C在(X,|·|)中也是弱紧的,因而在(X,|·|)中是可逼近的.

充分性.设D是X的有界闭凸均衡子集,满足int(D)≠Ø.设|·|为D所生成的Minkowski泛函,则|·|是X上的等价范数,并且D是(X,|·|) 的闭单位球.由充分性假设,C在(X,|·|)中是可逼近的.因此由引理1可知,C+D是闭的.进而由引理2,我们有:C是弱紧的.定理证毕.

最后,我们再来看一个例子.

例1 考虑有界序列空间(l∞,‖·‖∞),设C是(c0,‖·‖∞)的闭单位球.定义

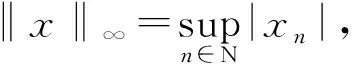
xn))2)1/2>1,

所以d|·|(e,C)≥1.这里,d|·|(e,C)表示在|·|意义下,e到C的距离.

|e-(e1+e2+…+ei)|=1+

因此d|·|(e,C)=1.所以在|·|的意义下,l∞在e处的度量投影为空,即C在(l∞,|·|)中不是可逼近的.

定理1中，当C是无界闭凸集时，我们可相应地考察C的局部弱紧性．闭凸集C称为是局部弱紧的，如果对于∀x∈C，都存在r>0，使得

C∩B(x,r)={y∈C:‖x-y‖≤r}

是弱紧的．显然，对于有界闭凸集，弱紧性与局部弱紧性是等价的；而对于整个空间X而言，X的局部弱紧性等价于X的自反性．容易验证，局部弱紧性意味着可逼近性，并且局部弱紧性在等价范数下是不变的．因此，如果C是X中的局部弱紧集，则对于X上的每个等价范数|·|，C在(X，|·|)中均是可逼近的．自然地，我们要问，反之是否成立？特别地，当C=X时，答案是否定的，因为在每个等价范数下，X在其自身中都是可逼近的，但X不一定是局部弱紧的(即自反的)．而当C≠X时，上述逆命题是否成立尚不可知．

[1] 周巍,罗正华.弱紧集的一个新特征[J].厦门大学学报:自然科学版,2013,52(3):309-311.

[2] Floret K.Weakly compact sets[M].Baffalo,USA:Springer-Verlag,1978.

[3] Diestel J.Sequences and series in Banach spaces[M].New York:Springer-Verlag,1984.

[4] Davis W J,Figiel T,Johnson W B,et al.Factoring weakly compact operators[J].J Funct Anal,1974,17:311-327.

[5] Cheng L X,Cheng Q J,Luo Z H.On some new characterizations of weakly compact sets in Banach spaces[J].Studia Math,2010,201(2):155-166.

[6] Cheng L X,Cheng Q J,Luo Z H,et al.Every weakly compact set can be uniformly embedded into a reflexive Banach space[J].Acta Math Sin(Engl Ser),2009,25(7):1109-1112.

[7] Singer I.The theory of best approximation and functional analysis[M].Philadelphia:SIAM,1974.

[8] Barbu V,Precupanu T.Convexity and optimization in Banach spaces[M].4th ed.Berlin,Germany:Springer-Verlag,2012.