基于混合智能粒子群算法的广义电源主动配电网优化配置

潘 超，焦薇羽，孟 涛，尹 杭

(1.东北电力大学电气工程学院，吉林 吉林 132012；2.长春供电公司，吉林 长春 130600)

基于混合智能粒子群算法的广义电源主动配电网优化配置

潘 超1，焦薇羽1，孟 涛1，尹 杭2

(1.东北电力大学电气工程学院，吉林 吉林 132012；2.长春供电公司，吉林 长春 130600)

研究广义电源接入主动配电网的优化配置问题。提出一种电压偏差指标。建立综合考虑投资经济效益、电压偏差及污染气体排放指标的多目标优化配置模型。提出一种混合智能粒子群算法，在优化过程中引入快速非支配排序策略、精英保留策略和拥挤距离计算策略以改善其全局搜索能力。对IEEE-33节点、PG&E-69节点配电系统进行计算，分析在不同负荷水平下各指标的变化情况，研究负荷变化时广义电源的最佳配置。研究表明，广义电源的接入与合理配置能够有效提高投资运行效益和系统电压稳定性，同时说明该方法能够保证配置方案的多样性和多目标优化过程的寻优性。

广义电源；主动配电网；电压稳定性；多目标优化；混合智能粒子群算法

0 引言

大规模分布式电源(Distributed Generator，DG)的接入将增加主动配电网(Active Distribution Network，ADN)规划运行的复杂性和不确定性[1-3]，甚至可能出现潮流逆变、电压质量恶化、供电可靠性降低等问题[4-6]。国内外已开展关于DG接入ADN的优化配置研究。文献[7]中考虑了源-荷侧的时序特性，建立以网损、停电损失为目标的数学模型，并通过遗传算法进行求解。文献[8]中建立了一种综合考虑投资成本、运营维护、燃料及废气排放费用的经济评价指标，研究不同场景下的DG规划问题。文献[9]中从配电系统负载水平、网损及电压质量的角度进行分析，采用混合粒子群算法求解模型。上述方法将多目标优化问题转化为单目标问题处理，权重系数的选取直接影响到优化结果，使得配置方案所考虑的因素并不全面。

主动配电网中广义电源指的是能发出一定有功或无功功率的装置，主要包括DG和电容器组。现有研究主要将DG和电容器组分开进行讨论，很少综合考虑广义电源(Generalized Power，GP)的优化配置问题。文献[10]建立投资成本、网损和电压指标的DG规划多目标优化模型，利用多目标粒子群算法研究了不同条件下的DG优化配置。文献[11]利用NSGA-II算法的快速非支配排序策略进行了电容器组在配电网中的多目标优化规划研究。目前，罕有文献从主动配电网的角度综合考虑GP的优化配置问题。因此，进行广义电源的优化配置对主动配电网的规划与运行具有重要的意义。

另一方面，电压偏差指标(Voltage Stability index，VSI)能为调度规划人员提供电网稳定运行依据，防止出现电压崩溃事故，因此建立考虑VSI的多目标数学模型是十分必要的。文献[12-14]中建立了相关VSI指标，研究DG接入配电网的电压稳定性问题，但是所建立的电压稳定性指标涉及数据较多，相关运行参数获取困难。

针对以上问题，本文基于网络潮流提出简易的电压偏差指标。从投资运行经济效益、电压偏差及污染气体排放指标的角度出发，建立综合考虑分布式电源和电容器组的多目标数学模型进行广义电源优化配置，提出一种混合智能粒子群优化算法。引入累积排序适应度赋值策略、精英保留策略和拥挤距离计算策略以改善多目标优化算法的参数选择过程和运行效率。对IEEE-33和PG&E-69节点配电网进行仿真计算，研究在不同负荷水平下经济效益、电压指标和气体排放的变化情况，确定不同负荷条件下广义电源的最佳配置。

1 GP多目标优化配置数学模型

1.1 投资运行经济效益

综合考虑投资、运行等成本效益和规划中的边际效益等方面进行建模，对应的数学模型f1为[15]

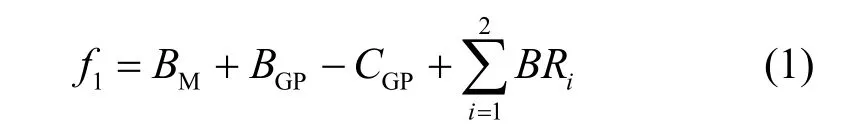
式中：BM、BGP和CGP分别为微网售电效益、GP发电效益和GP安装成本；BR为安装GP边际效益，其中BR1为延缓网架升级效益，BR2为网损改善效益。

1.2 电压偏差指标

考虑电力系统电压运行稳定性等方面进行建模，对应电压稳定性的数学模型f2为(具体推导过程参见附录A)

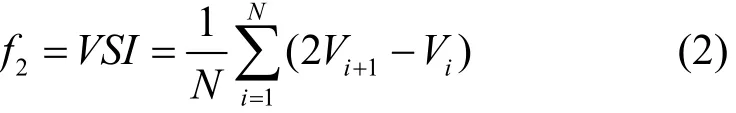
式中：Vi、Vi+1分别表示支路首、末端节点电压，i为节点编号；N为节点总数。

从上式可知，该电压稳定性指标仅与电压幅值相关，当支路末端节点的电压下降至首端节点的一半时，系统出现电压失稳现象。

1.3 污染气体排放指标

建立综合考虑CO2，NOx，SO2，CO等污染气体的排放指标，对应的数学模型f3为

式中：NGP为广义电源类型；Ng为污染气体排放类型；SGP(ij)为第i个节点j类广义电源发出的功率；wk为第k类污染气体的权重系数；ERjk为第j类广义电源的k类污染气体排放率；αj为碳排放系数比。

1.4 GP优化配置数学模型

综合考虑GP投资运行经济效益、电压偏差指标及污染气体排放指标的多目标优化数学模型为

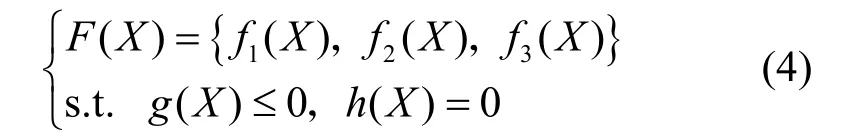
式中：g(X)为不等式约束条件；h(X)为等式约束条件；X为GP容量、位置等控制变量的集合。

等式约束条件主要为潮流约束。

式中：PGP_i和QGP_i分别为节点i处的GP有功出力和无功出力；PL_i和QL_i分别为节点i处的有功和无功负荷；Gij、Bij和δij为节点i，j之间的导纳参数和电压相角。

不等式约束条件主要包括GP安装容量、节点电压限值和支路电流限值。

2 基于HIPSO算法的GP优化配置

基于二阶粒子群优化算法[16]提出混合智能粒子群算法(HIPSO)。针对传统算法存在的“早熟”和“局部寻优”问题，在处理权重系数时采用线性递增权重的方法，HIPSO的速度、位置更新公式为

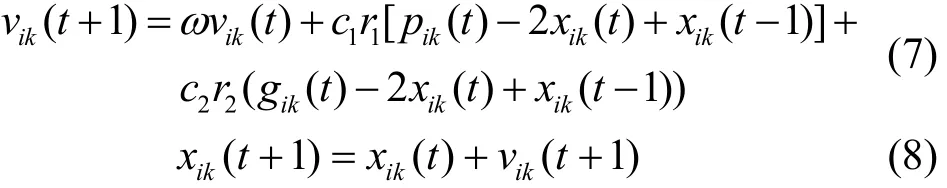
式中：vik(t)，xik(t)分别为粒子i在第t次迭代中第k维的速度和位置；pik(t)为粒子i在第t次迭代中第k维的个体极值点位置；g(t)为第t次迭代中全局极值点位置；ω为惯性权重；c1，c2为学习因子；r1，r2为[0,1]区间的均匀分布随机数。

在计算过程中引入累积排序适应度赋值策略、精英保留策略和拥挤距离计算策略[17-18]，具体流程如图1所示。

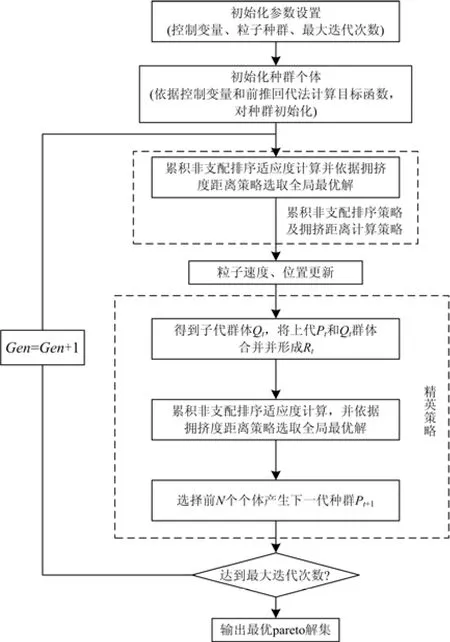
图1 HIPSO算法流程Fig. 1 Process of HIPSO algorithm

3 算例分析

以IEEE-33节点、PG&E-69节点配电系统[9]为例，对应的系统结构如图2、图3所示。GP包括风力发电(WT)、光伏发电(PV)、燃料电池(FC)、微型燃汽轮机(MT)、柴油机(DE)、电容器组(CB)，其投资成本及污染气体排放数据见表1。建立多目标数学模型，并采用HIPSO算法进行GP优化配置，其中粒子初始种群设置为90，迭代次数设置为200，惯性权重更新区间为[0.45，0.9]，学习因子c1=c2=1。

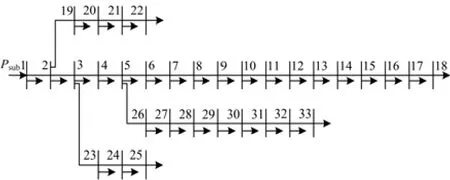
图2 IEEE-33节点配电系统Fig. 2 IEEE-33 node distribution network

图3 PG&E-69节点配电系统Fig. 3 PG&E-69 node distribution network

表1 广义电源相关数据Table 1 The related data of GP

3.1 考虑投资效益与电压稳定性的GP优化配置

图4 GP优化配置pareto解分布Fig. 4 Pareto solution of GP optimization

以IEEE-33节点为例，从投资运行效益与电压稳定性的角度对GP进行优化配置，其pareto解分布情况如图4所示。不难看出，投资运行经济效益与电压稳定性指标近似呈反比的关系，即提高负荷侧电压稳定性能需要以电网运行效益为代价。选取不同方案(A、B、C)进行分析，结果如表2和图5所示。

表2 典型方案的优化配置结果Table 2 Optimal results of typical schemes

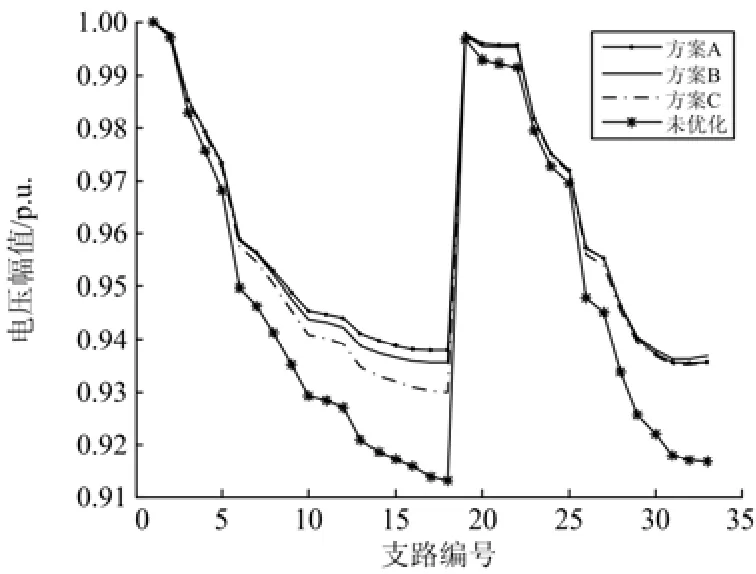
图5 不同方案的电压水平Fig. 5 Voltage level under different schemes

由表2和图5可知，GP接入能合理改善主动配电网的电压分布水平并降低网损，而对其进行优化配置可以进一步改善电网中分布式电源的渗透水平。优化后的GP配置方案在投资效益、VSI、网损方面均优于未优化的情况。其中， A类方案的电网VSI较高，投资运行效益最小；C类方案的电网VSI较低，投资运行效益最大；B类方案综合考虑系统运行稳定性与投资效益，其GP配置情况见图6。

图6 方案B的GP优化配置结果Fig. 6 Optimal allocation of GP in scheme B

3.2 考虑投资运行效益与气体排放的GP优化配置

考虑投资运行效益与气体排放指标对广义电源进行优化配置，其GP优化配置pareto解分布情况如图7所示。

图7 GP优化配置pareto解分布Fig. 7 Pareto solution of GP optimization

从图7可知，投资运行经济效益与气体排放指标近似呈反比关系，出现此情况的主要原因是在优化配置过程中考虑电容器组的优化配置，由于电容器组单位投资成本低，且无任何污染气体排放，因此，在分布式电源的优化配置过程中，同时考虑电容器组对DG优化配置过程的影响显得尤为重要。选取不同方案(D、E、F)进行分析，结果如表3和图8所示。由表3及图8可知，D类方案中电网VSI较高，网损较小，但投资运行效益最低且污染气体排放量较大；F类方案则与之相反。E类方案综合考虑投资运行效益和气体排放两个指标，其GP优化配置情况见图9。

表3 典型方案优化配置结果Table 3 Optimal results of typical schemes

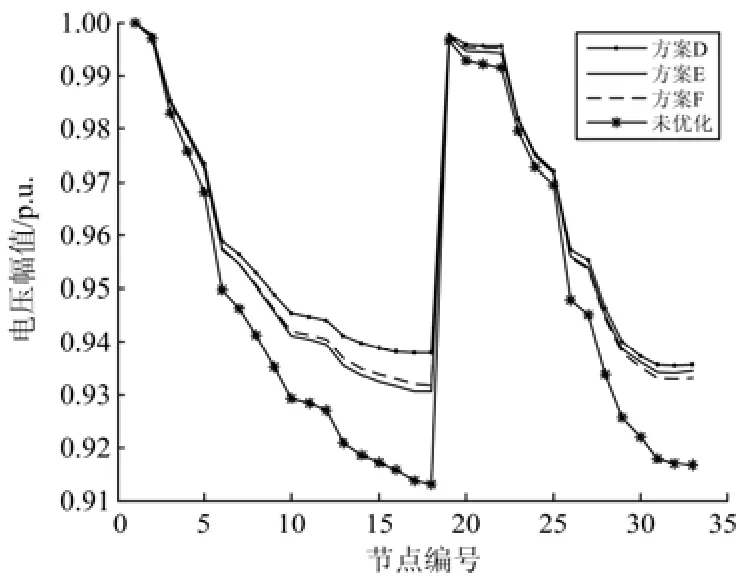
图8 不同方案的电压水平Fig. 8 Voltage level under different schemes

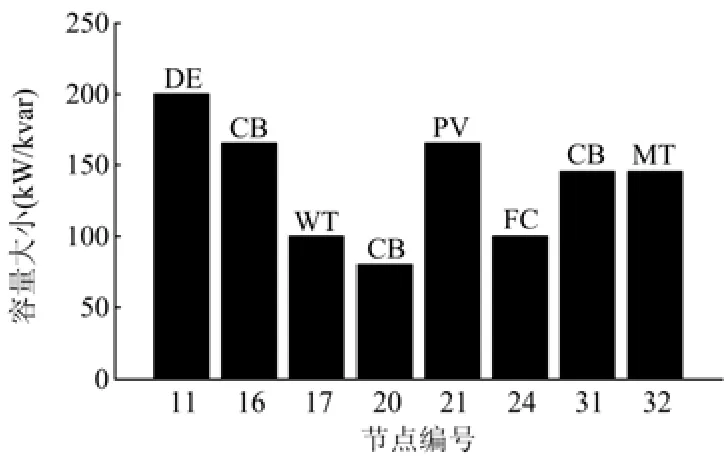
图9 方案E的GP优化配置结果Fig. 9 Optimal allocation of GP in scheme E

3.3 不同负荷水平下GP多目标优化配置

以IEEE-33节点系统和PG&E-69节点系统为例,考虑经济、技术、环境指标进行GP优化配置，同时计及不同负荷水平μ(μ1=0.7，μ2=1.0，μ3=1.3)。μ2=1.0时不同系统的GP优化配置pareto解见图10、11。不同条件下的GP优化配置结果及评价指标见表4。

由图10、图11可知，其Pareto解空间分布较为均匀，说明该算法具有良好的全局搜索能力；同时不同条件下关键指标的变化规律基本一致，反应出该算法在处理多目标优化问题时具有较好的参数识别能力。

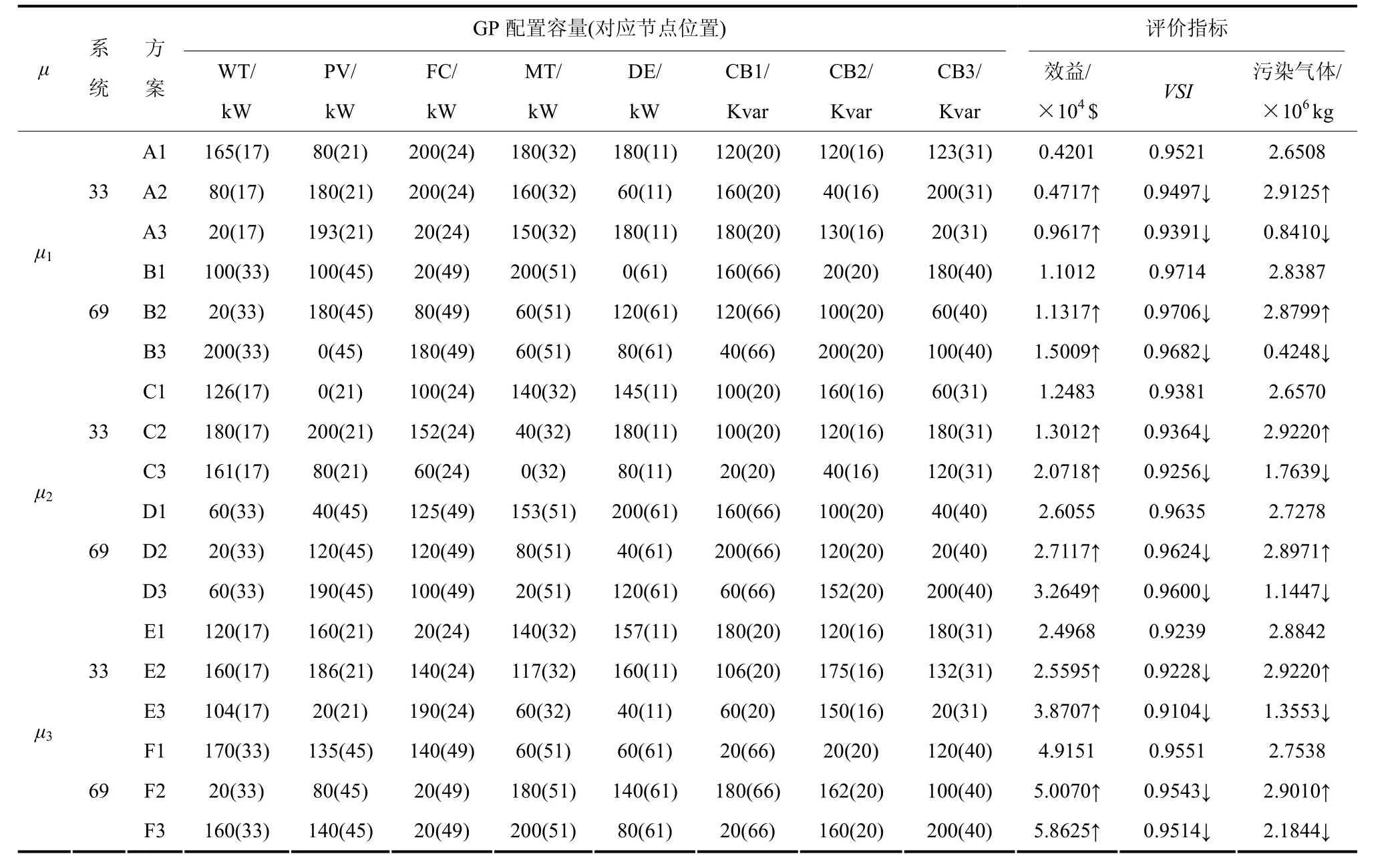
表4 不同负荷水平下GP优化配置情况Table 4 Optimal allocation of GP under different load rate

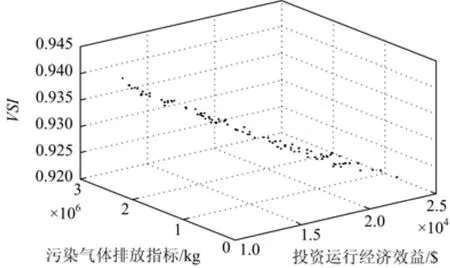
图10 IEEE-33节点GP优化配置pareto解分布Fig. 10 Pareto solution of GP in IEEE-33 node

图11 PG&E-69节点GP优化配置pareto解分布Fig. 11 Pareto solution of GP in PG&E-69 node

表4中以不同方案的第一种情况作为基准，另两种情况分别与之对比，结果表明不同条件下GP的优化配置方案存在明显区别，三种关键评价指标近似呈反比的关系。其中气体排放指标变化较为特殊，这是由于在优化配置方案中部分GP无气体排放的缘故。随着负荷水平的升高，对比GP优化配置方案与未优化方案，前者的投资运行效益增加，电压稳定性提高。另一方面，按照负荷增长趋势对比不同条件下的优化配置方案，广义电源接入主动配电网的容量随着负荷增加而增大，但电压稳定性却存在降低的问题，说明现有广义电源规模的增长趋势无法满足长远负荷增长的需求，因此需要从低碳发展的角度扩大广义电源规模，并合理规划源侧的资源利用。

4 结论

本文考虑经济、技术、环保等因素建立了多目标数学模型，研究广义电源在主动配电网中的优化配置，结论如下。

(1) 提出一种简单有效的电压稳定性指标，评价广义电源接入对主动配电网电压稳定性的影响。广义电源的合理配置可以有效提高主动配电网投资运行效益，改善系统运行电压水平。

(2) 提出一种HIPSO算法用于广义电源的多目标优化配置，引入累积排序适应度赋值策略、精英保留策略和拥挤距离计算策略以提高寻优能力和计算效率。

(3) 在进行广义电源的优化配置时，投资运行效益、电压稳定性和气体排放三者近似成反比的关系。随着负荷水平的升高，广义电源的接入与合理规划能够有效提高供电服务部门的经济效益，改善电力用户的电压质量，为调度运行人员提供全面合理的辅助决策。

[1] 陈海东, 庄平, 夏建矿, 等. 基于改进萤火虫算法的分布式电源优化配置[J]. 电力系统保护与控制, 2016, 44(1): 149-154. CHEN Haidong, ZHUANG Ping, XIA Jiankuang, et al. Optimal power flow of distribution network with distributed generation based on modified firefly algorithm[J]. Power System Protection and Control, 2016, 44(1): 149-154.

[2] 王健, 谢桦, 孙健. 基于机会约束规划的主动配电网能量优化调度研究[J]. 电力系统保护与控制, 2014, 42(13): 45-52. WANG Jian, XIE Hua, SUN Jian. Study on energy dispatch strategy of active distribution network using chance-constrained programming[J]. Power System Protection and Control, 2014, 42(13): 45-52.

[3] 潘超, 孟涛, 蔡国伟, 等. 广义电源多目标优化配置与运行[J]. 电网技术, 2015, 39(12): 3505-3512. PAN Chao, MENG Tao, CAI Guowei, et al. Multiobjective optimal configuration and operation of generalized power sources[J]. Power System Technology, 2015, 39(12): 3505-3512.

[4] 张建华, 曾博, 张玉莹, 等. 主动配电网规划关键问题与研究展望[J]. 电工技术学报, 2014, 29(2): 13-23. ZHANG Jianhua, ZENG Bo, ZHANG Yuying, et al. Key issues and research prospects of active distribution network planning[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 13-23.

[5] 程杉, 陈民铀, 黄薏宸. 含分布式发电的配电网多目标无功优化策略研究[J]. 电力系统保护与控制, 2013, 41(10): 45-50. CHENG Shan, CHEN Minyou, HUANG Yichen. Multi objective reactive power optimization of distribution system penetrated with distributed generation[J]. Power System Protection and Control, 2013, 41(10): 45-50.

[6] 施泉生, 郭良合, 张孝君. 综合考虑多主体经济效益的分布式电源优化配置研究[J]. 电力系统保护与控制, 2016, 44(1): 85-91. SHI Quansheng, GUO Lianghe, ZHANG Xiaojun. Research on optimal configuration of distributed generation considering economic benefits of the multi-agent[J]. Power System Protection and Control, 2016, 44(1): 85-91.

[7] 李亮, 唐巍, 白牧可, 等. 考虑时序特性的多目标分布式电源选址定容规划[J]. 电力系统自动化, 2013, 37(3): 58-64. LI Liang, TANG Wei, BAI Muke, et al. Multi-objective locating and sizing of distribution generators based on time-sequence characteristics[J]. Automation of Electric Power Systems, 2013, 37(3): 58-64.

[8] ZHAOYU W, BOKAN C, JIANHUI W, et al. Robust optimization based optimal DG placement in microgrids[J]. IEEE Transactions on Smart Grid, 2014, 5(5): 2173-2182

[9] AMAN M M, JASMON G B, BAKAR A H A, et al. A new approach for optimum simultaneous multi-DG distributed generation units placement and sizing based on maximization of system load ability using HPSO(hybrid particle swarm optimization) algorithm[J]. Energy, 2014, 66(1): 202-215.

[10] PARTHA K, TANUSHREE B, CHANDAN K C. Planning of renewable DGs for distribution network considering load model: a multi-objective approach[J]. Energy Procedia, 2014, 54(3): 85-96.

[11] DULCE F P, CARLOS H A, ANTONIO G M. NSGA-II with local search for a multi-objective reactive power compensation problem[J]. Electrical Power and Energy Systems, 2012, 43(9): 313-324.

[12] AMAN M M, JASMON G B, MOKHLIS H, et al. Optimal placement and sizing of a DG based on a new power stability index and line loss[J]. Electrical Power and Energy Systems, 2012, 43(9): 1296-1304.

[13] 徐琳, 卢继平, 汪洋, 等. 电力系统节点电压稳定指标的研究[J]. 电网技术, 2010, 34(3): 26-30. XU Lin, LU Jiping, WANG Yang, et al. Research on nodal voltage stability index of power system[J]. Power System Technology, 2010, 34(3): 26-30.

[14] 任洪伟, 韩丛英, 裴玮, 等. 基于多目标优化模型的分布式电源选址方案研究[J]. 电力系统保护与控制, 2013, 41(24): 64-69. REN Hongwei, HAN Congying, PEI Wei, et al. Research on distributed generation locating based on multi objective optimization model[J]. Power System Protection and Control, 2014, 41(24): 64-69.

[15] ALI Z, SHAHRAM J, ASHKAN R K. A fuzzy environmental technical economic model for distributed generation planning[J]. Energy, 2011, 36(5): 3437-3445.

[16] 卢志刚, 杨国良, 张晓辉, 等. 改进二进制粒子群优化算法在配电网络重构中的应用[J]. 电力系统保护与控制, 2009, 37(7): 30-34. LU Zhigang, YANG Guoliang, ZHANG Xiaohui, et al. Reconfiguration of distribution network based on improved particle swarm optimization[J]. Power System Protection and Control, 2009, 37(7): 30-34.

[17] 冯士刚, 艾芊. 带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用[J]. 电工技术学报, 2007, 22(12): 146-152. FENG Shigang, AI Qian. Application of fast and elitist non-dominated sorting generic algorithm in multi objective reactive power optimization[J]. Transactions of China Electrotechnical Society, 2007, 22(12): 146-152.

[18] 陈征, 肖湘宁, 路欣怡, 等. 含光伏发电系统的电动汽车充电站多目标容量优化配置方法[J]. 电工技术学报, 2013, 28(6): 238-249. CHEN Zheng, XIAO Xiangning, LU Xinyi, et al. Multiobjective optimization for capacity configuration of PV-based electric vehicle charging stations[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 238-249.

(编辑 葛艳娜)

Optimal allocation of generalized power sources in active distribution network based on hybrid intelligent particle swarm optimization algorithm

PAN Chao1, JIAO Weiyu1, MENG Tao1, YIN Hang2
(1. School of Electrical Engineering, Northeast Dianli University, Jilin 132012, China 2. Changchun Power Supply Company, Changchun 130600, China)

Optimal allocation of generalized power sources in active distribution network is researched. A simple index of voltage stability is put forward. Considering the investment and operation benefit, the stability of voltage and the pollution emissions of generalized power sources in active distribution network, a multi-objective optimization planning model is established. A hybrid intelligent particle swarm optimization algorithm is proposed to solve the optimal model. In order to improve the global search ability, the strategies of fast non-dominated sorting, elitism and crowding distance are adopted in this algorithm. Finally, the model and algorithm by different load level of IEEE-33 node and PG&E-69 node are tested to find the best configuration of GP. The computed result shows that with the generalized power reasonable access to the active distribution network, the investment benefit and the voltage stability of the system are improved, and the proposed algorithm has better global search capability.

This work is supported by National High-tech R & D Program of China (863 Program) (No. SS2014A A 052502).

generalized power; active distribution network; voltage stability; multi-objective optimization planning; hybrid intelligent particle swarm optimization algorithm

10.7667/PSPC150373

2015-08-11；

2016-01-15

潘 超(1981-)，男，博士，副教授，研究方向为电力系统稳定与仿真;

焦薇羽(1989-)，女，硕士研究生，研究方向为分布式电源规划、主动配电网；

孟 涛(1990-)，男，通信作者，在读研究生，研究方向为分布式电源规划、主动配电网。E-mail: 494344848@ qq.com

国家高技术研究发展计划(863)资助项目(SS2014A A 052502)；长江学者和创新团队发展计划资助项目(IRT114)