基于定向自适应核分布的滑动轴承油膜失稳信号分析

刘小峰， 罗宏林， 罗义林

(重庆大学 机械传动国家重点实验室，重庆　400044)

基于定向自适应核分布的滑动轴承油膜失稳信号分析

刘小峰1， 罗宏林， 罗义林

(重庆大学 机械传动国家重点实验室，重庆400044)

摘要：在定向Wigner分布的基础上，提出了定向自适应核时频分布。该方法将用于单通道实信号分析的自适应核分布扩展到复信号，并定义了正交双通道融合复信号的定向自适应核分布。为了验证该方法，利用转子试验台模拟滑动轴承旋转机械的失稳故障以获取数据，分析结果表明该方法不仅能够提取系统在某一截面的周期性振动特征，而且能够揭示转子在指定运动状态时的旋向。与单通道信号的自适应核分布相比，正交双通道融合复信号的定向自适应核分布能更好地抑制交叉项以及具有更高的频率分辨率，此外定向自适应核时频分布与全谱分析结果相吻合，从而验证了该方法的有效性。

关键词：滑动轴承；油膜失稳；定向Wigner分布；定向自适应核分布

时频分析是分析非平稳信号的有效工具。在众多的时频分析方法中，Wigner-Ville分布是最基本的，具有时频分辨率高等优良特性[1]。但由于Wigner-Ville分布是双线性变换，对于多分量信号，存在严重的频率混叠与交叉项。目前Wigner-Ville分布的应用主要通过核函数的设计来抑制交叉项，主要原理为在模糊域利用固定的核函数对信号的模糊函数进行滤波，从而抑制交叉项[2]。然而，一种固定的核只能对某一类型的信号具有良好的近似性能[3]。为了使核函数对信号具有良好的自适应性，Baraniuk等[4]提出了基于信号的自适应核时频分析，使核函数根据信号的特点进行自适应调整，并提出了自适应优化核函数设计准则，设计了径向高斯核分布。王胜春等[5]提出了自适应径向抛物线核时频分布并将其应用于滚动轴承故障诊断。刘小龙等[6]提出了自适应最优核时频分布并将其应用于地震储层预测。滕伟等[7]提出了基于Gabor变换的时频滤波，成功地提取出了汽轮机半速涡动故障频率。但上述的分析方法只针对单通道振动信号的分析处理，为了描述转子在某一横截面上的瞬时平面运动状态，Lee等[8-9]将传统的单向实信号的Wigner分布进行了扩展用于复信号，从而提出了定向Wigner分布。该方法通过将正交复信号变换为正反向解析信号，有效地避免了定向Wigner分布存在的频率混叠与二次交叉项等问题。定向自适应核分布是在定向Wigner分布与自适应径向高斯核时频分布的基础上定义的，具有两者的优势，既能抑制交叉项、提高信号时频分布集聚度，还能表示轴承转子系统某一截面瞬时运动状态。

本文首先介绍了全谱分析技术的原理，再给出了定向Wigner分布的推导过程，最后定义了定向自适应核时频分布。然后研究分析了滑动轴承-转子系统在油膜涡动和油膜振荡下实测振动信号的定向自适应核分布特性。通过将转子和轴承座振动信号的定向自适应核分布与单通道信号的自适应核分布进行对比，最后总结了定向自适应核分布在描述滑动轴承转子系统失稳状态时的有效性及优越性。

1定向核时频分布

1.1全频谱分析

Bently Nevada Corporation公司提出了全频谱分析技术，并在旋转机械状态监测与故障诊断领域应用广泛[10-11]。该方法通过融合双通道传感器信号避免了在单独计算转子XY方向两个信号的频谱时，其相对相位关系以及转子旋向等信息的丢失，从而可以直接重构出滤波后的转子轴心轨迹图。在数学上，椭圆轨迹可以视作旋转频率相同但方向相反的两个圆向量的和。因此，在全谱图中ω处滤波后的轴心轨迹可以表示为两个正反向量的和，当正向圆半径Rω+大于反向圆半径Rω-时，转子的旋向为正进动(转子的旋向与自转方向相同)，当正向圆半径Rω+小于反向圆半径Rω-时，转子的旋向为反进动(转子的旋向与自转方向相反)。此外，椭圆轨迹的长轴与坐标横轴的倾角为正反分量的初始相位差，即(βω-αω)/2。

R(t)=Rω+ej(ωt+αω)+Rω-ej(ωt+βω)

(1)

如图1所示，全谱图可以由滤波后的轴心轨迹的前进动和反进动的向量半径推导出。全谱图中横坐标表示了频率(正半轴表示前向进动频率，负半轴表示反进动频率)，纵坐标表示峰峰值[8]。

图1　全谱分析的数学推导过程Fig.1 Procedure for obtaining a full spectrum

1.2定向Wigner分布

为了描述转子在某一横截面上的瞬时平面运动状态，Lee和Han将传统的单向实信号的Wigner分布进行了扩展用于复信号，从而提出了定向自Wigner分布以及互Wigner分布的概念[8]。

设x(t)和y(t)分别表示两个正交的单通道的正弦实信号，定义复信号p(t):

p(t)=x(t)+j·y(t)

(2)

式中复信号p(t)表示一作椭圆运动的向量，由于椭圆运动可以表示为两个旋向相反的圆运动向量之和, 可以利用欧拉公式将转频为ω的向量p(t)表示为极坐标形式：

p(t)=pf(t)+pb(t)=pfejwt+pbe-jwt

(3)

而实信号x(t)和y(t)可以根据傅里叶系数展开为：

(4)

式中xc、xs、yc和ys表示对应的傅里叶系数。

则正反进动的圆向量可以表示为：

(5)

(6)

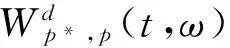
(7)

定向自Wigner分布包含了转子轴心轨迹的形状和旋向信息，互Wigner分布包含了转子轴心轨迹倾角信息。

1.3定向自适应核分布

为了抑制Wigner-Ville分布交叉项，使信号的自主项得到很好的分离，人们设计了多种时频分布。它们可以统一表示成Cohen类双线性时频分布[3]

(8)

式中,A(θ,τ)为信号s(t)的模糊函数，定义为

(9)

式中,Φ(θ,τ)为低通的核函数，通过设计不同的核函数就能得到不同的时频分布特性。然而一种固定的核只能对某一类型的信号具有良好的近似性能。为了克服核时频分布中核对信号的敏感性，Baraniuk[4]提出了基于信号的高斯核时频分布。

(10)

(11)

由式(9)可知Φ(θ,τ)最终被一维的扩展函数σ(ψ)参数化表达，所以设计与信号相匹配的核函数可以通过求解最优化的扩展函数σ(ψ)来实现，即求解以下优化问题

(12)

约束条件为

(13)

(14)

式中,A(r,ψ)为模糊函数在极坐标中的表示形式，α为高斯核函数的体积，一般选择2≤α≤5[3]。式(13)限制了优化问题的范围为径向高斯核类(低通函数)，式(14)限制了最优核的体积(低通函数的范围)。

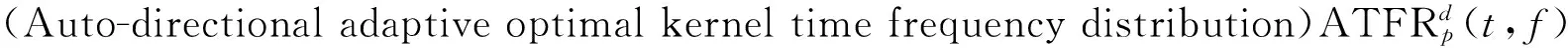
(15)

式中,φ(τ,ν)Apf(τ,ν)和Apb(τ,ν)为前向模糊函数与后向模糊函数，定义为

(16)

(17)

ejθt-jωτdθdτ

(18)

式中,Apb,f(τ,ν)为互模糊函数，定义为

(19)

定向自适应核分布包含了转子时频分布特征和旋向信息，互自适应核分布包含了转子轴心轨迹倾角信息，并且能很好地抑制交叉项。

2油膜涡动与油膜振荡信号分析

2.1实验装置介绍

为了验证定向自适应核分布在滑动轴承油膜失稳故障诊断中的应用效果，采用北京测振仪器厂的ZT-3型转子振动试验台模拟仿真滑动轴承支撑转子系统油膜失稳故障信号。如图2所示，试验台采用直流并励电动机经半挠性联轴器直接驱动转轴。电动机的额定电流为2 A，最大输出功率为250 W。电动机可由手动调速器控制实现0～10 000 r/min范围内的无极调速。为了测量转子和轴承座的位移振动信号，在转轴中间平面上正交(0°,90°)安装了OD-Y911801型电涡流非接触式探头，为了测量轴承的加速度振动信号，分别在滑动轴承支座以及油膜振荡轴承支座上正交(0°,90°)安装型号为ICP 608A11的加速度传感器。所有的传感器通道都被连接到基于Labview的多通道信号采集系统，实现了信号的实时采集、存储与显示。基于上述转子振动试验平台与数据采集系统，本文先后仿真了滑动轴承支撑转子系统在不同工作转速下的运行状态。

图2　滑动轴承柔性转子实验台Fig.2 Test bench and its main components

在滑动轴承支撑转子系统起动阶段随着工作转速的逐渐升高，系统依次经历了平稳运行、系统共振、油膜涡动、油膜振荡等运行状态。反之，在停机阶段随着工作转速逐渐降低，系统依次经历了油膜振荡、油膜涡动、系统共振、平稳运行等运行状态。

根据转子的升速瀑布图，可知滑动轴承支撑转子系统在工作转速5 500 r/min下将发生油膜涡动现象，转频X1=91.67 Hz。当工作转速升高到6 200 r/min时将发生油膜振荡现象，转频X2=103.33 Hz。转子与轴承座的时域振动信号及频谱如图3～图6所示。其中信号的采样频率为fs=2 048 Hz，信号总长度为N=8 192。

图3中能看到转子在油膜涡动状态下的转频X1以及油膜涡动频率fowl=0.475X1=43.5 Hz。图4轴承座加速度信号的频谱图中能看到涡动频率fowl、转频X1及其倍频成分2X1、3X1等更加丰富的信息。图5中能看到油膜振荡状态下的转频X2以及油膜振荡频率fowp=0.476X2=49.25 Hz，对应了转子振动试验台的一阶临界转速2 955 r/min。图6轴承座的加速度振动信号的频谱图中能看到振荡频率fowp、转频X2及二倍频2X2、以及复杂的耦合频率信息。可以知道基于轴承座加速度振动信号的状态检测与基于转子位移信号的状态检测相比所获得的描述系统振动状态的信息更加丰富。

图3 转子在油膜涡动状态下的振动信号及其频谱Fig.3Vibrationsignalanditsspectrumoftherotorduringoilwhirl图4 轴承座在油膜涡动状态下的振动信号及其频谱Fig.4Vibrationsignalanditsspectrumofthebearingpedestalduringoilwhirl图5 转子在油膜振荡状态下的水平振动信号及其频谱Fig.5Vibrationsignalanditsspectrumoftherotorduringoilwhip图6 轴承座在油膜振荡状态下的水平振动信号及其频谱Fig.6Vibrationsignalanditsspectrumofthebearingpedestalduringoilwhip

图7　转子在油膜涡动状态下的定向自适应核分布及全谱图Fig.7 Directional adaptive optimal kernel distribution and full spectrum of the vibration signal of the rotor during oil whirl

2.2定向自适应核分布分析

在第1小节的理论基础上基于式(1)和式(16)计算系统在油膜涡动以及油膜振荡状态下复信号的自适应核分布与全谱图，截取2 048个数据点进行计算，采样频率为2 048 Hz，采样时间为1 s，结果如图7～10所示。

图7与图8分别给出了转子与轴承座在油膜涡动状态下的振动信号的定向自适应核分布图，图中定向自适应核分布的负半轴幅值远远大于对应正半轴处的幅值，可知转子在油膜涡动状态下反向旋进。图7中能看到转频X1、涡动频率fowl=0.475X1，并且涡动频率幅值出现周期性变化，变化周期为ΔT1=0.22 s ，对应了全谱图中涡动频率fowl与其边频X1-fowl的距离Δf1=1/ΔT1=4.58 Hz。图8中可以看到幅值随时间变化的涡动频率fowl、转频X1及其倍频信息2X1、3X1以及 1X1+fowl、2X1+fowl等频率耦合信息。定向自适应核分布图对照全谱图不仅能清晰地看到系统径向振动信号时频图的各频率成分的具体大小，还能知道转子在油膜涡动状态下反向旋进。值得指出的是，耦合频率信息2X1+fowl与倍频成分3X1在图中交替在出现。

滑动轴承支撑转子系统在油膜涡动状态下由于振动剧烈，激发了油膜涡动频率fowl与转频X1的多倍频成分以及他们的和差组合频率成分[12]，即mX1±nfowl(其中m,n∈N+)。而耦合频率2X1+fowl与倍频3X1在图中交替出现揭示了此时转子的运动状态。转子带动润滑油高速旋转，由于润滑油具有黏性，轴颈由于转子自重在轴承中作偏心旋转时，形成进油口断面大于出油口断面的油楔，由于油液不可压缩，多余的油液会将转子推向前进，形成了转子的涡动运动[12]，这时转子的涡动频率fowl与转频X1耦合，形成耦合频率信息2X1+fowl。与此同时，由于油楔的存在，油液进入油楔之后压强升高，远大于轴颈另一侧油液的压强，压强差使转子受到一个指向轴瓦圆心的力，该力会使转子的偏心减小，油楔的开口扩大，使转子涡动消失，此时转子的振动激发倍频成分3X1，由于楔口扩大，轴颈两端的压强差减小，转子偏心扩大，油楔楔口减小，使转子再次发生涡动，从而引起了耦合频率信息2X1+fowl与倍频成3X1的交替出现。

图8　轴承座在油膜涡动状态下的定向自适应核分布及全谱图Fig.8 Directional adaptive optimal kernel distribution and full spectrum of the vibration signal of the pedestal during oil whirl

图9与图10分别给出了转子与轴承座在油膜振荡状态下的定向自适应核分布图。图9中只能看到油膜振荡频率fowp，并且负半轴的幅值远远大于正半轴，转子在油膜振荡时反向旋进。图10中能看到明显的二倍转频2X2，并且其负半轴幅值远大于正半轴幅值，转子在油膜振荡状态反向旋进。还能看到振荡频率fowp、转频X2以及耦合频率2X2-fowp。值得指出的是在全谱图的边缘部分出现了复杂的频率耦合信息，并且在自适应核分布图中随着时间变化间歇性出现，这些频率成分为2X2+fowp、3X2-fowp、4X2-3fowp，并且间隔为Δf2=X2-2fowp=4.83 Hz。

由于油膜的涡动频率接近转子系统的一阶固有频率，系统发生油膜共振，激烈的振动同样也会激发油膜振荡频率fowp和转频X2的多倍频成分以及这两个主振频率的和差组合频率成分，并且此时还伴随着轴颈和轴承的摩擦，出现了密集的耦合频率带。当出现密集的耦合频带时，频率成分之间的最小距离Δf0。

(20)

当Δm=1,Δn=2时Δf0取最小，此时Δf0=0.046 8X2。当X2=103.33 Hz时，Δf0=4.83 Hz，与观察结果Δf2相符，从形成机理方面验证了定向自适应核分布的有效性。以上的结论也再次证明基于轴承座加速度振动信号的状态检测与基于转子位移信号的状态相比所获得的描述系统振动状态的信息更加丰富。

图9　转子在油膜振荡状态下的定向自适应核分布及全谱图Fig.9 Directional adaptive optimal kernel distribution and full spectrum of the vibration signal of the rotor during oil whip

图10　轴承座在油膜振荡状态下的定向自适应核分布及全谱图Fig.10 Directional adaptive optimal kernel distribution and full spectrum of the vibration signal of the pedestal during oil whip

图11　系统在油膜涡动状态下单通道信号的自适应核分布及频谱Fig.11 Adaptive optimal kernel distribution and spectrum of single channel signal of the system during oil whirl

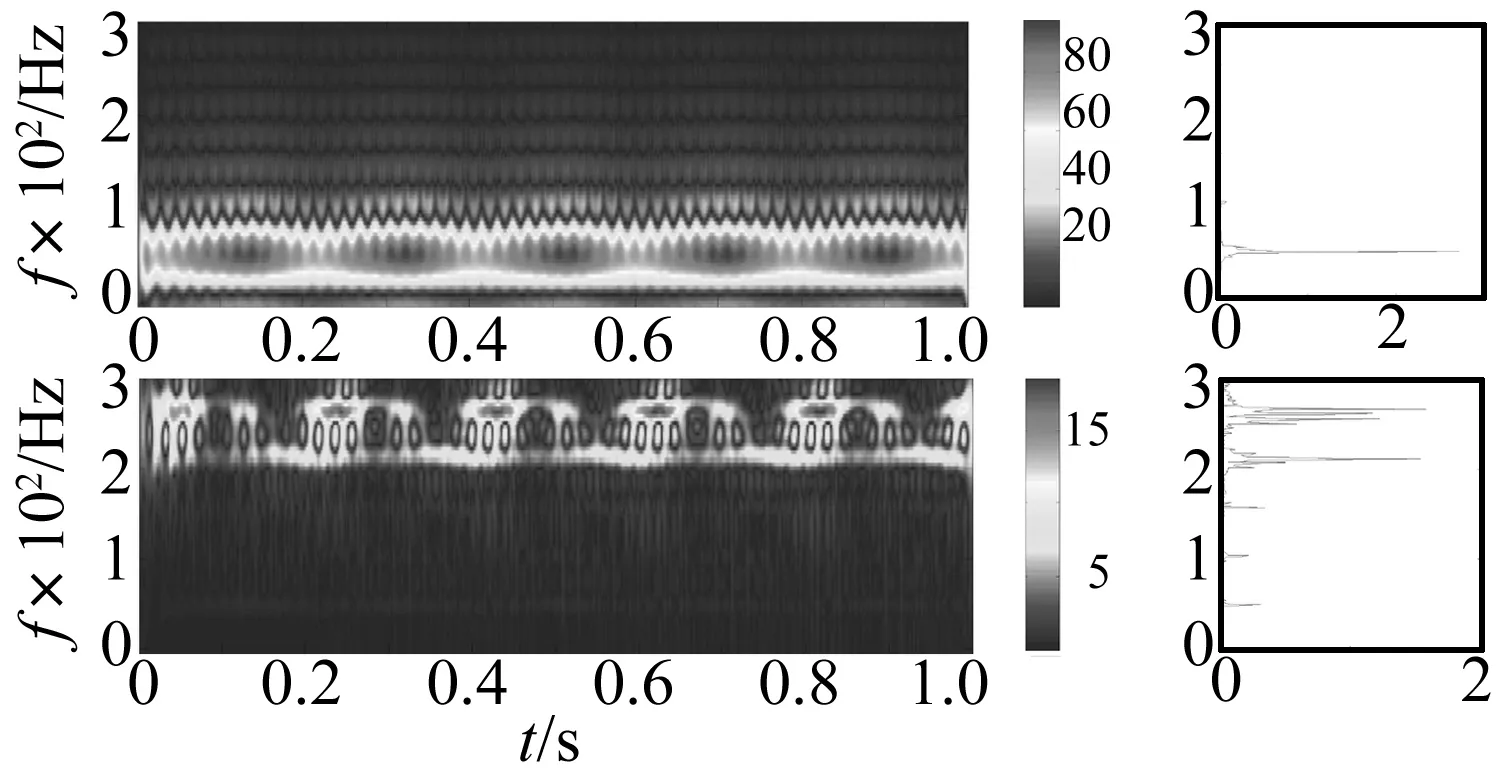
图12　系统在油膜振荡状态下单通道信号的自适应核分布及频谱Fig.12 Adaptive optimal kernel distribution and spectrum of single channel signal of the system during oil whip

为了进一步比较定向自适应核分布与普通自适应核分布的区别，在第1小节的理论基础上基于式(10)与式(11)计算了转子在油膜涡动以及油膜振荡状态下的自适应核分布与频谱图，计算时截取2 048个数据点进行计算，采样频率为2 048 Hz，采样时间为1s，结果如图11与图12所示。图11与图12给出了系统在油膜涡动与油膜振荡状态下单通道信号的自适应核分布，图中可以明显地看到交叉项，而且频率分辨率较低。与单通道的信号的自适应核分布相比，基于正交融合信号的定向自适应核分布能更好地抑制交叉项的产生，并且能看到系统在运行过程中的瞬时平面运动状态以及转子的旋向等信息。

3结论

为了综合描述滑动轴承支撑转子系统在油膜失稳状态下的运行状况，本文在定向Wigner分布与自适应核分布的基础上定义了定向自适应核分布。本方法将传统的实信号自适应核分布理论进行了扩展用于分析由正交单通道信号融合而成的复信号，不仅能够揭示转子轴承系统在油膜涡动以及油膜振荡状态下振动信号的时频分布特征，而且能够表征转子在指定频率处的进动旋向。

实测信号的分析结果表明，将定向自适应核分布与全谱图结合进行综合描述转子轴承系统的运行状态具有十分明显的优势，全谱图可以定量地给出各频率信息的大小，而定向自适应核分布可以准确地给出各频率成分出现的时间，随着时间变化而出现的各种特点。所以，将定向自适应核分布与全谱图结合来综合描述转子轴承系统的运行状态具有实际工程应用的价值。此外，试验结果还表明基于轴承座加速度振动信号的状态监测与传统的基于转子位移振动信号的状态监测相比，数据采集过程更为方便，而且所获得的描述系统油膜失稳状态下振动信息更加丰富。

参 考 文 献

[1] 胡广书. 现代信号处理教程[M]. 北京: 清华大学出版社, 2004.

[2] 邹剑, 陈进, 董广明. 裂纹转子识别中Wigner-Ville 分布与小波变换的比较[J]. 机械强度, 2003, 25(6): 591-595.

ZOU Jian, CHEN Jin, DONG Guang-ming. Comparision Wigner-Ville distribution with wavelet transform in identification of cracked rotor[J]. Journal of Mechanical Strength, 2003, 25(6):591-595.

[3] 李亚安,王军,雷粉霞.自适应核时频分布在抑制交叉项中的运用[J].系统工程与电子技术, 2004, 26(11): 1567-1569.

LI Ya-an, WANG Jun, LEI Fen-xia. Application of adaptive kernel time-frequency distribution in cross-components suppression, Systems Engineering and Electronics,2004,26(11):1567-1569.

[4] Baraniuk R G,Jones D L.Signal-dependent time-frequency analysis using a radially gaussian kernel[J].Signal Processing,1993,32(3):263-284.

[5] 王胜春,韩捷,李志农,等.自适应径向抛物线核时频分布及其在故障诊断中的应用 [J].机械强度, 2007, 29(2):180-184.

WANG Sheng-chun, HAN jie, LI zhi-nong, et al. Adaptive radial parabola kernel representation and its application in the fault diagnosis[J]. Journal of Mechanical Strength,2007, 29(2):180-184.

[6] 刘小龙,王华,赵淑娥,等. 自适应最优核时频分布在地震储层预测中的应用[J]. 中南大学学报:自然科学版, 2012, 43(8): 3114-3120.

LIU Xiao-long, WANG hua, ZHAO Shu-e, et al. Application of adaptive optimal kernel time-frequency representation in reservoir prediction[J]. Journal of Central South University:Science and Technology, 2012, 43(8):3114-3120.

[7] 滕伟,安宏文,马志勇,等.基于时频滤波的汽轮机半速涡动故障成分提取[J].振动与冲击,2015,34(3):178-182.

TENG Wei, AN Hong-wen, MA Zhi-yong, et al. Semi-speed oil whirl fault component extraction in a steam turbine based on time-frequency filtering[J].Journal of Vibration and Shock,2015,34(3):178-182.

[8] Lee C, Han Y. The directional wigner distribution and its application [J]. Journal of Sound and Vibration, 1998, 216: 585-600.

[9] Lee C, Han Y. Directional wigner distribution for order analysis in rotating/reciprocating machines [J]. Mechanical Systems and Signal Processing, 1999, 13:723-737.

[10] Southwick D. Using full spectrum plots [J]. Orbit, 1993, 14: 19-21.

[11] Southwick D. Using full spectrum plots part 2 [J]. Orbit, 1994, 15: 11-15.

[12] 沈庆根,郑水英. 设备故障诊断[M]. 北京: 化学工业出版社, 2006.

Method for analysis of instable journal bearing signal based on directional adaptive optimal kernel distribution

LIU Xiao-feng, LUO Hong-lin, LUO Yi-lin

(The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)

Abstract:The directional adaptive optimal kernel distribution was defined based on the directional Wigner distribution. The method extends the adaptive optimal kernel distribution, which is restricted to analyze the real-valued signal, to process the constructed complex-valued signal obtained from the journal bearing supported rotor system operating in the condition of oil film instability. To verify the method, a rotation test bench was built to simulate rotating machinery faults. The analysis of the experimental data shows that the periodic vibration characteristics and the rotation direction within the plane of interest can be easily discovered. Besides, the results of the directional adaptive optimal kernel distribution method keep consistent with those by the full spectrum scheme, which verifies the effectiveness of the method.

Key words:journal bearing; oil-film instability; directional Wigner distribution; directional adaptive optimal kernel distribution

基金项目：国家自然科学基金资助项目(51475052);中央高校基本科研业务费(CDJZR14110004);中国博士后基金(2015M582519)

收稿日期：2015-01-25修改稿收到日期：2015-05-18

中图分类号:TH17;TP206

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.024

第一作者 刘小峰 女，博士，副教授，1980年9月生