“小题”也需“大做”——由一道习题引发的一节课

◇陈新福 陈 艳

“小题”也需“大做”
——由一道习题引发的一节课

◇陈新福 陈 艳

北师大版教材六年级上册第一单元“圆”的“练习一”中，有这样一道习题，如图1所示：

图1

我对这道习题进行有效开发，设计成了一节课，从而真正凸显了这道习题的价值。

【教学过程】

一 多角度探究圆与正方形的关系

教师出示图2①。

师：请观察，这幅图中圆与正方形的关系是怎样的？

生：这个圆是正方形内最大的圆。

生：圆的直径等于正方形的边长。

教师接着出示图2②、图2③。

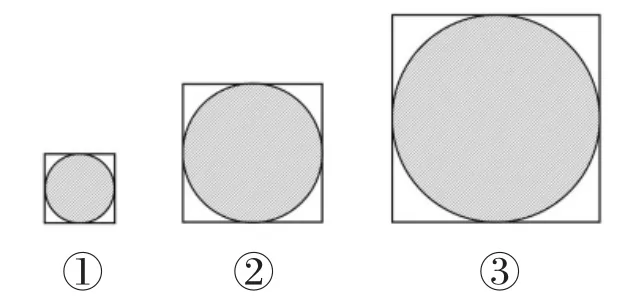
图2

师：想一想，正方形的边长变大，正方形面积与圆面积会发生怎样的变化？

生：正方形面积和圆面积也会变大。

在讨论交流的基础上，请学生完成下表。

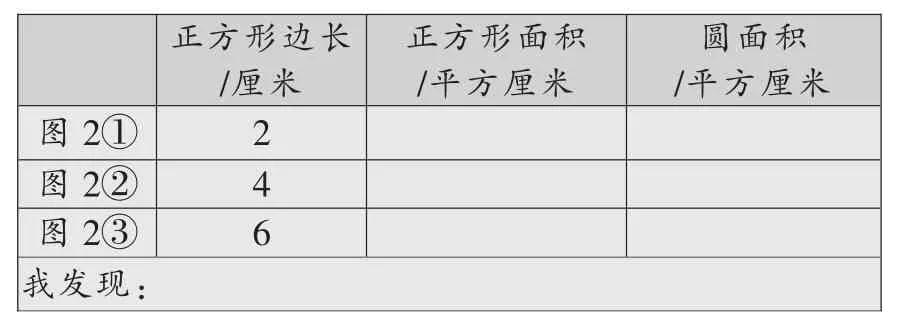
圆面积/平方厘米图2①正方形边长/厘米2正方形面积/平方厘米图2②图2③我发现：46

师：通过讨论，我们发现当正方形边长（圆直径）变大时，正方形面积（圆面积）也变大。那么，这个圆与正方形之间还存在什么关系呢？圆面积占正方形面积的几分之几？

生：计算出来的结果是一样的。

师：通过计算来寻找关系，是一种很好的思路。再看图3，如果圆的半径用字母r表示,那么，圆面积是多少？

图3

生：S圆=πr2。

师：那么圆外正方形的面积是多少呢？

生：S正=r2×4=4r2。

引导学生发现，圆面积÷正方形面积=πr2÷4r2=

师小结：因为π是一个常数，圆面积和正方形面积的关系就是一个固定的关系，即

师：这个固定关系除了用分数的形式来表示，还可以用什么形式表示？（引导学生用比的形式与百分数的形式表示）

二 进一步探究

教师出示下面的问题，请学生根据面积之间的关系解决问题，题目如下：

如图4，正方形面积为20㎡，求圆的面积。

图4

因为有前面的讨论与交流，学生比较容易地就算出了圆的面积。

师：运用圆与正方形的面积比，能使复杂的问题简单化。图5中阴影部分的面积你会求吗？

图5

生：阴影部分面积就是正方形中最大的圆的面积。

师：在这个正方形中，你能设计出类似的与圆面积相等的其他图案吗？请画出示意图，并说明理由。

投影展示学生作品，如图6所示：

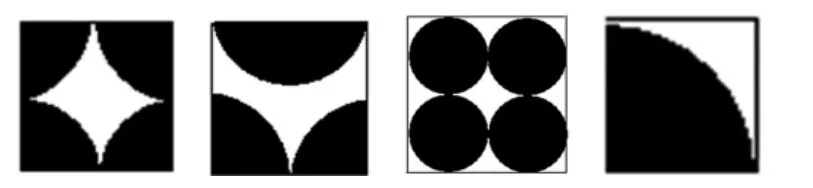
图6

同时组织学生讨论如下的问题。

1.还有不同方案吗？

2.这些图案都符合要求吗？哪些是你一眼就能看出符合要求的？并由此进行分类。

3.除了计算，还有什么办法能说明面积相等？

4.我们把圆缩小可以画出4个小圆，同理我们还可以画出其他的图形吗？缩小为9个可不可以？16个呢？（如图7）

（此环节尝试让学生用比的知识解释圆半径同比扩大或同比缩小后圆的面积和不变）

图7

师：这些正方形内圆的面积都相等，那么你们能否从图中发现圆面积与半径之间的变化关系呢？

（引导学生把图7中后三个正方形中的圆分别与第一个进行比较）

生：反过来说，当半径扩大若干倍时，圆的面积就扩大为这个倍数的平方。

师：说得真棒！那么圆与哪些图形可能也存在固定的关系呢？请你课后再研究研究。

三 利用圆与正方形的关系解决问题

1.基于原题的练习。

（1）一张正方形纸的边长为4厘米，把这张纸剪成一个最大的圆。剩下部分的面积是多少？

（2）一张正方形纸的面积是80平方厘米，把这张纸剪成一个最大的圆，这个圆的面积是多少平方厘米？

2.基于设计的练习。

（1）求阴影部分的面积（如图8）。

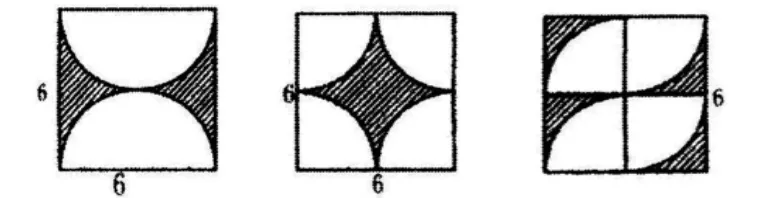
图8

（2）四张边长都是12厘米的正方形铁皮，分别按图7剪下不同规格的圆片。哪张铁皮剩下的废料多？

（3）基于拓展的练习。

如图9，我们在圆中画一个最大的正方形。如果这个圆的半径是r，圆的面积是多少？正方形的面积呢？圆的面积与正方形面积有什么关系？

图9

（作者单位：浙江衢州市大成小学）