军区后方仓库弹药储备布局模型研究

高 军，雷 敉，陈 金（军械工程学院装备指挥与管理系，河北石家庄 050003）



军区后方仓库弹药储备布局模型研究

高 军，雷 敉，陈 金
（军械工程学院装备指挥与管理系，河北石家庄 050003）

摘 要：军区后方仓库弹药储备布局是否合理，关系到能否安全而及时地对前线部队进行保障，从而间接影响战争走向。本文在运用有关军事规则对后方仓库弹药储备布局问题进行详细分析的基础上，应用多目标决策的思想建立了数学模型，进而运用改进的遗传算法对模型进行了求解，从而获得后方仓库弹药储备布局的最优方案。

关键词：弹药储备布局；多目标优化；遗传算法

1　引 言

军区后方仓库储存的弹药往往品种繁多、批次不一，各种弹药的技术安全性能差异较大，如何安全而合理地将弹药存放在各个库房之中，既要能确保弹药的储存安全，又要便于管理和发出，是军区后方仓库弹药管理中需要解决的首要问题，也是军区后方仓库弹药保障能力提升的重点环节。

2　问题分析

为了安全及时地为作战部队供应相应品种和数量的弹药，必须综合考虑各种影响因素，深入研究其特点，运用相关理论建立数学模型，选择适当的优化算法，从而获得仓库布局和需储弹药品种及数量的最优方案［1］。

后方仓库弹药储备布局的本质问题是选库和定量，即从备选洞库中选择合适的洞库供战时使用，并且确定每个洞库所储弹药的品种和数量。作为战时弹药保障的重要一环，其运作过程的基本要求是及时、安全。为了顺利完成战斗任务，应在最短时间内将部队所需弹药运到。而仓库安全性的高低实际上决定了弹药的生存能力，影响到部队作战任务的完成。另外，从费用角度来看，选择洞库的多少又直接关系到整个仓库系统的总消耗费用。所以问题可归结为一个追求选用仓库平均及时度最大（供应总消耗时间最少）、平均安全度最大（弹药安全储存能力最大）和选用仓库总数量最少的多目标决策问题［2］。

弹药储存的安全性和供应到位的及时性均是反映仓库布局优劣的综合性指标，分别称之为仓库的安全度和及时度，它们受多种相关因素的影响［3］。由军事专家的分析和军事规则的限制可知：仓库储量、地理环境、储存条件和防御能力是影响安全度的主要因素；而考虑到弹药装卸和运输的特殊性，其运输速度不能超过应有的限定值，同时洞库内现有弹药的堆码情况等因素也会影响到具体的装卸时间。故设置运输时间和装卸时间为影响及时度的主要因素。由此，从众多因素中选出库房位置、库房容量、储存条件、设备条件、运输时间和装卸时间这六项主要因素对仓库弹药储备布局决策问题进行研究，忽略其它因素的影响。主要影响因素如图1所示。

图1　层次关系分析图Fig.1 Diagram of hierarchical relationship

3　模型建立

设洞库数量最少目标（A1，A2，…，An）为n个备选洞库，M为预测的弹药总储备量。要求在以平均安全度最大、平均及时度最大、选用洞库数量最少作为目标的前提下确定满足供求约束条件的仓库地点，即给出一选点方案，既要使所选择的仓库满足安全性和及时性的要求，又要使选用洞库的数量最少，且其储存的弹药能满足部队的需要。可列出数学模型：

式中：S表示选用洞库的平均安全度，T表示选用洞库的平均及时度，si表示第i个洞库的安全度，ti表示第i个洞库的及时度，xi代表库房选择：

1选择、0不选，N（Ø）表示选用洞库的数量，Ø代表某一布局方案，Mi表示第i个洞库的容量，M表示任务需要储备的弹药总量，n代表备选仓库总数。

定义1：称方案Ø是可行的，如果相对于该方案的洞库容量满足：

式中：（i1，i2，…，im）为选用洞库的编号，它是（1，2，…，n）子列的一个排列，1≤m≤n。

定义2：对序列（Mi1，Mi2，…，Mim）若存在k，1 ≤k≤m≤n，使得

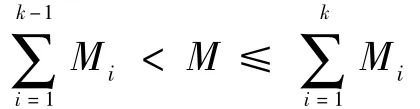
则称k为该序列相对于M的临界下标。

可得结论，设k为递减数列Mi1≥Mi2≥…≥Mim相对于M的临界下标，则k个洞库可保证选用洞库的数量最少。这样可以将选用洞库数量最少这个目标转化为约束，于是模型可以修改为：

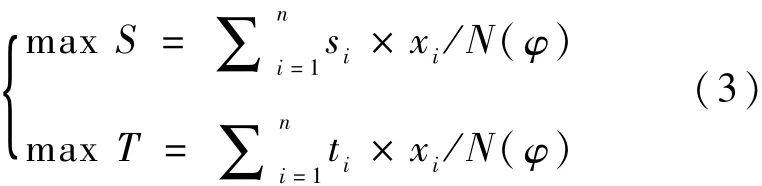
式中，k为满足条件洞库的最少个数，如果再去掉任意一个洞库，其容量就会少于需要储存的弹药总储备量，不能满足供求约束。为体现这一思想［3］，去掉容量最小的洞库，选用洞库总容量就会小于需要的弹药总储备量，可推得：若去掉容量大的洞库，选用洞库总容量就更小于需要的弹药总储备量。将约束条件用0 -1状态变量xi表示，模型又可为：

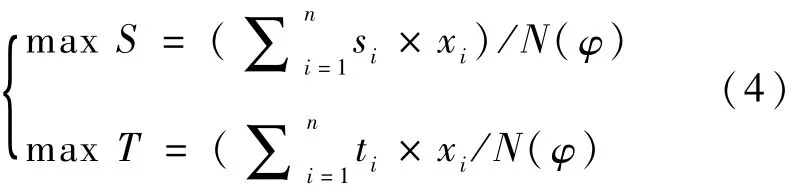
式中，ω为选用洞库中除去容量最小的洞库后剩余洞库所组成的集合。

4　算法设计

遗传算法并不要求有明确的教学方程式，只用编码和适应度表示问题，搜索不依赖于梯度信息，比较适合后方仓库弹药储备布局这类多目标优选问题的求解［4］。在后方仓库弹药储备布局多目标优化模型中需要用到综合性指标安全度和及时度，可应用加权平均法、专家打分法或层次分析法综合各自相关影响因素求得。遗传算法具体内容如下所述。

4.1编码策略

染色体采用由0或1所组成的代码串表示。对于一个在n个仓库中选优的问题，用一个有n位数的代码串表示，每位代表一个仓库，1表示选择该洞库，0表示不选该洞库，则一个n位数的代码串（即染色体）即表示了一种洞库选择方案。若参与评价的适应度函数是已知的，则一个染色体即对应一个可计算的适应度值。

4.2生成初始种群

随机产生大小为N的初始种群，种群中的每个个体（染色体）的长度为n位。遗传算法以这N个个体数据作为初始点开始迭代。

4.3确定适应度函数

适应度函数的建立是整个遗传算法中一项极其重要的工作。它是遗传算法中评价解集好坏的依据，不仅关系到优化问题最终能否找到最优解，而且还影响着遗传算法的收敛速度。由于在模型中总数量最少这个目标已转化为约束条件，因此只需考虑平均安全度最大和平均及时度最大这两个目标的优化。在遗传算法中个体适应度的大小代表个体优劣与否，故其适应度函数可直接由目标函数加权表示为

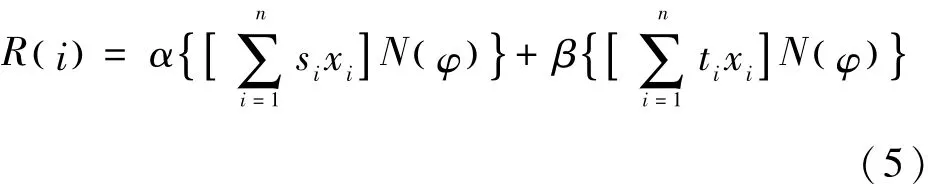
式中：α+β=1，α为平均安全度指标占总指标的权重，β为平均及时度指标占总指标的权重。

对于目标函数中约束条件的处理，采取惩罚策略，即对于每个可行（满足约束条件）的染色体，算出其相应的适应度函数值，而对于每个不可行的染色体，给予一个很大的惩罚，即：

式中：eval（Ph）表示第h个染色体的适应度，Ph代表第h个染色体；R（h）为适应度函数；经程序实际计算表明，惩罚项S的选择与算法中个体多样性保持的问题密切关联，将其作为一个很大的正整数即可满足要求。

4.4遗传操作

遗传操作包括选择、交叉、变异3种操作算子，本文采用标准遗传操作，选择操作是排序选择+最佳个体保存法，交叉操作是依据交叉概率的单点交叉，变异操作是依据变异概率的单基因突变。

4.5交叉、变异概率的自适应确定

交叉算子在遗传操作中起核心作用，主要用来产生新个体，实现算法的全局搜索能力［5］。因此，本文设计了与进化代数相关的交叉概率：

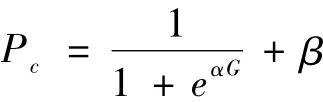
式中：G为进化代数，α、β为定常系数，α代表交叉概率的变化曲率；β代表交叉概率的收敛极限。

为此设计了如下与遗传进化代数和个体适应度相关的自适应变异概率：

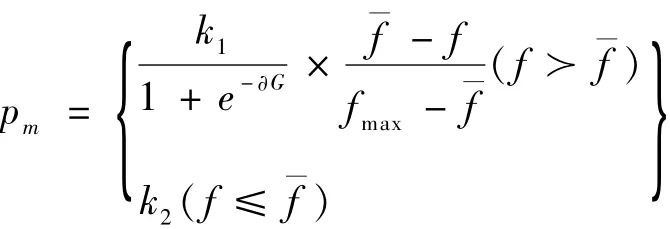
其中：α，k1，k2为定常系数，α代表变异概率的变化速度，k1与具体问题有关，是为保证遗传算法不退化为随机搜索，Pm所能取到的最大值，k2为1个比较小的变异概率，通常取0.001；f¯为当前群体平均适应度值；f为当前个体适应度值；G为进化代数；fmax为当前群体中最大个体适应度值。

比较三种遗传操作（选择、交叉、变异）后选出的最优个体，分别计算其适应度，将适应度最大的个体保留下来，再与随机产生的N-1个个体组成新种群，循环执行三种遗传操作，直至达到规定的迭代次数。设经过N΄次迭代后（N΄≤规定的迭代次数），所选出的最优个体的适应度不再增加，表明全局最优个体从第N΄代开始出现。该个体即为在本次运算过程中所获得的最优个体，亦即后方仓库弹药储备布局的最优方案。

5　模型仿真

假定军区某后方仓库接收一批3000吨弹药，现有20个备选库房可供选择，各库房特征描述如表1（库房位置、储存条件、设备条件由军事专家通过德尔菲法获得，采用1 -9刻度表示）所示。

由于样本库房数为20，所以染色体采用一个20位数的二进制代码表示。设置初始种群大小为50，迭代次数100，开始运行算法。运算过程中，最优个体从第62次迭代开始出现，其二进制编号为01010110101001101011，适应度大小为0. 5913，选用库房总容量为3105吨。运算结果如图2所示。

故选用库房为2、4、6、7、9、11、14、15、17、19、20号共11个库房。

表1　备选库房特征描述表Tab.1 Feature descrip tion of alternative storehouse

图2　搜索路径图Fig.2 G raph of Search Path

6　结 论

本文根据军事规则和仓储实际情况对后方仓库弹药储备布局问题进行了较为详细的研究，然后建立了相应的多目标优化数学模型，进而用改进的遗传算法对模型进行了求解，从而获得后方仓库弹药储备布局的最优方案。研究成果已在实践中获得了成功运用，同时也提供了解决类似问题的一种思路。

参考文献：

［1］ 黄童圣，李良春，孙士泽等，军械仓库布局调整决策模型［J］.物流科技，2010（2）：117 -120.

HUANG Tongsheng，LI Liangchun，SUN Shi-ze etal. Decision -making Model on the Distributing Adjustment of Ordnance DePots［J］.Logistics Technology，2010（2）：117 -120.

［2］ 酆明，王凭慧，李东升.军械仓库布局调整决策模型［J］.运筹与管理，2000，6（2）：48 -54.

FENG M ing，WANG Pinghui，LI Dongsheng.Decision -making Model on the Distributing Adjustment of Ordnance DePots［J］. OPerations Research and Management Science，2000，6（2）：48 -54.

［3］ 沈浩，孙琰，卢宏锋.战场弹药储备布局探索性分析决策方法［J］.军械工程学院学报，2007，4（2）：13 -18.

SHEN Hao，SUN Yan，LU Hong-feng.Decision -making Method of ExPloratory Analysis for the Storage and Position of Ammunition in the Battlefield［J］. Journal of Ordnance Engineering College，2007，4（2）：13 -18.

［4］ 易良廷，李咏治.后勤装备物资临战储备仓库多目标选择［J］.物流科技，2011（12）：225 -227.

YI Liangting，LI Yongzhi，Multi-objective Selection of Logistics EquiPment DePots in Ware PreParation［J］. Logistics Technology，2011（12）：225 -227.

［5］ 陈长征，王楠.遗传算法中交叉和变异概率选择的自适应方法及作用机理［J］.控制理论与应用，2002，19 （1）：41 -43.

CHEN Changzheng，WANG Nan.AdaPtive Selection of Crossover and Mutation Probability of Genetic Algorithm and its Mechanism［J］.Control Theory&APPlications，2002，19（1）：41 -43.

高 军 男（1971 -），山东青岛人，副教授，主要研究方向为装备保障工程，供应链管理。

雷 敉 男（1991 -），湖南邵阳人，硕士生，主要研究方向为物流管理理论与应用

。

Research on Storage Layout Model of Rear Ammunition Depot

GA0 Jun，LEIM i，CHEN Jin
（DePartment EquiPment Command and Management，Ordnance Engineering College，Shijiazhuang 050003，China）

Abstrac t：Storage Layout of Rear ammunition dePot is the key factor to suPPort the front trooPs safely and tim ely and it indirectly affects the direction of w ar.This PaPer analyzed storage layout of rear ammunition dePot in detail based on relevantm ilitary rules.A mathematicalmodel is established by using multi-objective decision making.Then the model is solved using im Proved genetic algorithm，and the oPtimal Program of the storage layout of rear amm unition dePot is obtained.

Key w ords：storage layout of rear amm unition dePot；multi-objective oPtim ization；genetic algorithm

中图分类号：TJ 410.89

文献标识码：A