基于观测器与小波变换的UAV作动器故障检测

钟麦英，薛 婷（北京航空航天大学仪器科学与光电工程学院，北京 100191）



基于观测器与小波变换的UAV作动器故障检测

钟麦英，薛 婷
（北京航空航天大学仪器科学与光电工程学院，北京 100191）

摘 要：为提高无人机飞行控制系统的安全性和可靠性，将观测器方法与小波变换相结合，针对无人机飞行控制系统作动器故障检测问题开展研究。在基于观测器构造残差的基础上，通过引入小波变换，产生一组包含不同频率作动器故障的残差，将残差产生器设计归结为小波基函数选取和H2/H2性能指标最优化问题。利用小波变换的时频局部化特性，在保证性能指标最优的同时，可减小故障检测延时，且产生的一组残差能够检测较宽频带内的作动器故障。基于某型无人机的Simulink仿真结果表明，该方法的检测快速性好，可检测故障的频率范围宽，且对闭环飞行控制系统中的微小故障具有较高的灵敏度，有效降低了漏报率。

关键词：无人机；故障检测；闭环；观测器；小波变换

1　引 言

无人机（Unmanned Aerial Vehicle，UAV）在各领域日益广泛的应用，对飞行控制系统的安全性和可靠性提出了新的挑战。作动器作为飞行控制系统的重要执行机构，不可避免会发生故障，严重时将威胁UAV的飞行安全。因此，针对UAV飞行控制系统作动器故障检测方法的研究具有重要意义［1］。

近年来，国内外针对UAV飞行控制系统故障诊断的研究以基于解析模型的方法居多［1～2］，其中一种是观测器方法，其通过设计故障检测滤波器（Fault Detection Filter，FDF）构造残差，并进行残差评价实现故障检测［1］。UAV在飞行过程中受到大气紊流、随机噪声等未知扰动的影响，鲁棒性问题是UAV飞行控制系统故障诊断研究的重要方面［2］。目前，较为常用的是基于Hi/H∞Hi/ H∞性能指标最优化的鲁棒故障检测方法［3］。该方法将FDF设计转化为Hi/H∞Hi/H∞性能指标最优化问题，在残差评价阶段，通常根据干扰信号范数的上确界确定阈值，而这种阈值设定容易引起闭环飞行控制系统中微小故障漏报。文［4］中将FDF设计描述为H2/H2性能指标最优化问题并求解，但其最优解在频域等效为窄频带滤波器，导致漏报率较高，且检测延时较大，在实际应用中受到限制。文［5］从残差评价的角度出发，通过引入小波变换（Wavelet Transform，WT），利用其时频局部化特性，克服了H2/H2最优解存在的缺陷。此外，基于WT的时频分析也有利于闭环飞行控制系统中持续时间短且能量较小的故障的提取与检测。

本文结合UAV作动器故障检测的实际需求，将观测器方法与小波变换相结合进行UAV作动器故障检测。利用小波变换的时频局部化特性，优化基于观测器的FDF设计使H2/H2性能指标最优，同时减小检测延时；进而对产生的一组包含不同频率故障的残差进行残差评价，实现较宽频带内的作动器故障检测；最后，以某型UAV为例进行Simulink仿真实验，验证了方法的有效性。

2　UAV飞行控制系统故障模型

考虑一类六自由度固定翼UAV，以其纵向运动系统为例，采用小扰动线性化方法建立如下所示大气扰动下的UAV纵向线性化运动方程［6］：

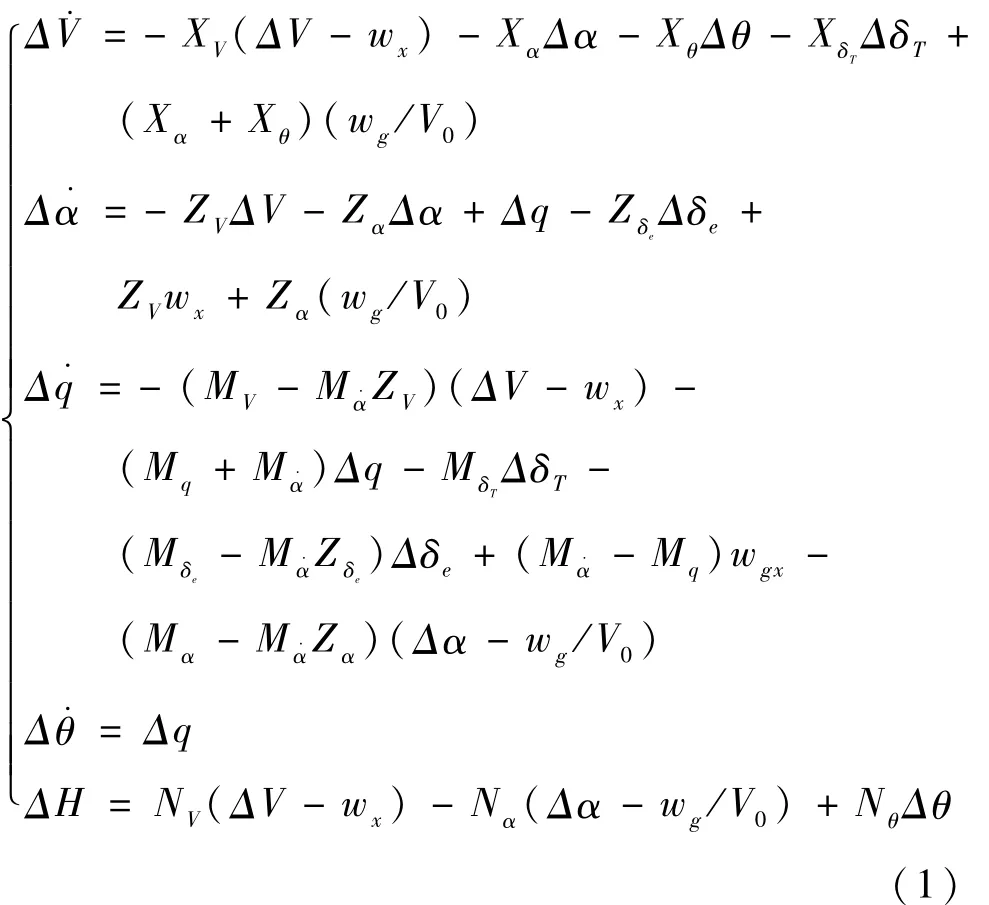
式中：V0为基准运动速度，ΔV，Δα，Δq，Δθ，ΔH分别为速度、迎角、俯仰角速率、俯仰角和高度的增量；Δδe，ΔδT为升降舵偏角和油门杆偏角增量；wx，wgwg为前向和垂向风速，wgx为wg沿前向的梯度；XV，Xα，Xθ，Xδ，ZV，Zα，Zθ，Zδ，MV，Mα，，Mq，TeMδ，Mδ，NV，Nα，Nθ为常值参数，由飞机构型参数Te及基准状态气动导数决定，可由风洞试验获得。

UAV飞行控制系统是典型的闭环系统，作动器作为其执行机构，不可避免会发生卡死、增益或偏差等故障，不失一般性，均可将其描述为加性故障。选取状态变量x=［ΔV Δα Δq Δθ］T，系统输入u =［ΔδeΔδT］T，可量测状态变量为系统输出y=［ΔV Δα Δq Δθ］T，量测噪声为V，大气紊流干扰为dw=［wxwgwgx］T，则大气扰动下的UAV纵向飞行控制系统故障模型表示如下：

式中：x∈Rkx，u∈Rku，y∈Rky，A、B、C为已知的系统矩阵，Bd为干扰系数矩阵。

3　问题描述

在UAV飞行控制系统中，闭环反馈控制的引入增强了系统的鲁棒性，导致故障发生早期或幅值较小的故障带来的影响可能被控制作用所掩盖，使得故障检测的难度增大［7］。

考虑采用观测器方法实现UAV作动器故障检测，首先需进行残差产生器设计。针对UAV纵向飞行控制系统（2），将干扰统一描述为d =，则有

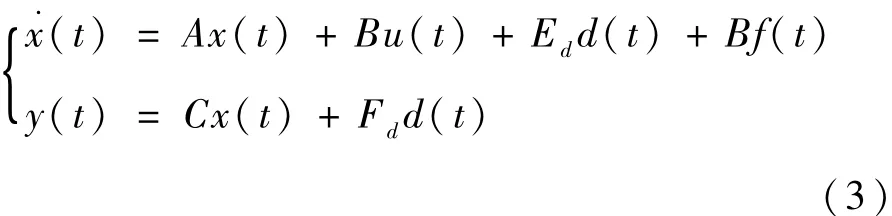
式中：Ed=［Bd0］，Fd=［0 Iky］，I为单位矩阵，0为零矩阵。假设干扰d∈L2范数有界，（C，A）可观测，且对于ω∈［0，∞）均为行满秩。

针对上述系统（3），设计如下状态观测器：

则残差产生器的定义如下所示：

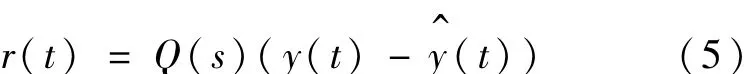
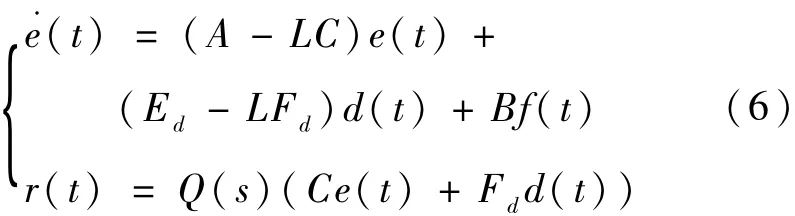
则残差在频域可表示为：

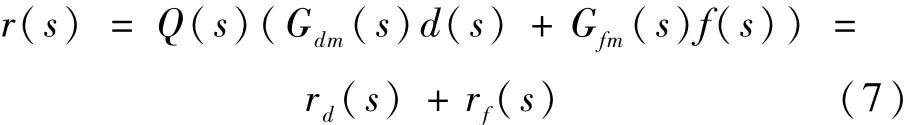
式中：Gdm（s）=C（sI-A+LC）-1（Ed-LFd）+Fd，Gfm（s）=C（sI-A+LC）-1B，rd（s）=Q（s）Gdm（s）d（s），rf（s）=Q（s）Gfm（s）f（s）。

因难以实现残差对干扰完全解耦，通常可采用H2范数‖Q（s）Gfm（s）‖2和‖Q（s）Gdm（s）‖2描述残差对故障的敏感性和对干扰的鲁棒性，将FDF设计转化为如下H2/H2性能指标最优化问题［4］：

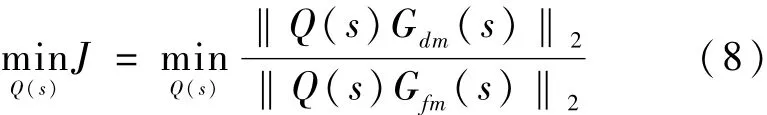
从而残差产生器设计归结为：设计L和Q（s），使（A-LC）渐近稳定，且性能指标J最优。文献［4］给出了式（8）所示最优化问题的解Qopt（s）：

式中：Λmax和Vmax为广义特征方程的最大特征值和对应特征向量，Pωopt（ω）为ωopt处的窄频带选频滤波器，当ω=ωopt时性能指标最优。

在残差评价阶段，选取适当的残差评价函数J（r）和阈值Jth，按照如下判定逻辑判断UAV作动器是否发生故障：

4　UAV作动器故障检测系统设计

基于传统方法所设计的选频滤波器Pωopt（s）的频带较窄，而时域长度较长，导致漏报率较高，且检测延时较大，难以满足UAV作动器故障检测实时性和低漏报率的需求。考虑到小波变换的时频局部化特性，本文将观测器方法与小波变换相结合进行作动器故障检测系统设计。

4.1小波变换

设ψ（τ）为小波基函数，信号η（τ）∈L2的小波变换的定义如下［8］：

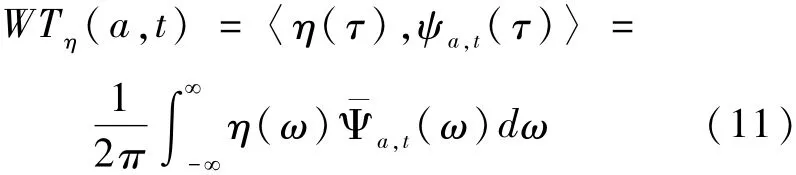
在进行故障信号分析时，小波基函数和分解尺度的选取至关重要。db N小波是工程中广泛应用的正交小波函数族，且N越小，基函数的时域支撑长度越短，检测延时越小。综合考虑作动器故障检测的实际需求，本文选取db1小波作为小波变换的基函数。此外，分解尺度不宜过大，否则缓变故障的提取效果变差，且检测延时增大。

4.2作动器故障检测系统的残差产生

考虑UAV纵向系统（3），在观测器方法的基础上引入小波变换，设计如下残差产生器：

根据式（7）和小波变换的线性可加性，有

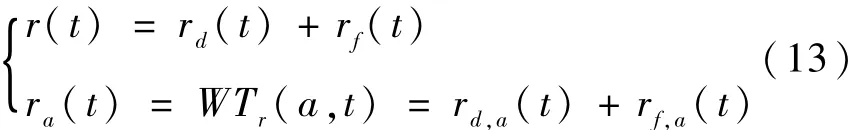
式中：rd，a（t）=WTrd（a，t），rf，a（t）=WTrf（a， t），rd（t）=q（t）gdm（t）d（t），rf（t）=q（t）gfm（t）f （t）；q（t）、gdm（t）、gfm（t）为Q（s）、Gdm（s）、Gfm（s）的时域表示。

以rd，a（t）为例，根据式（11）可得

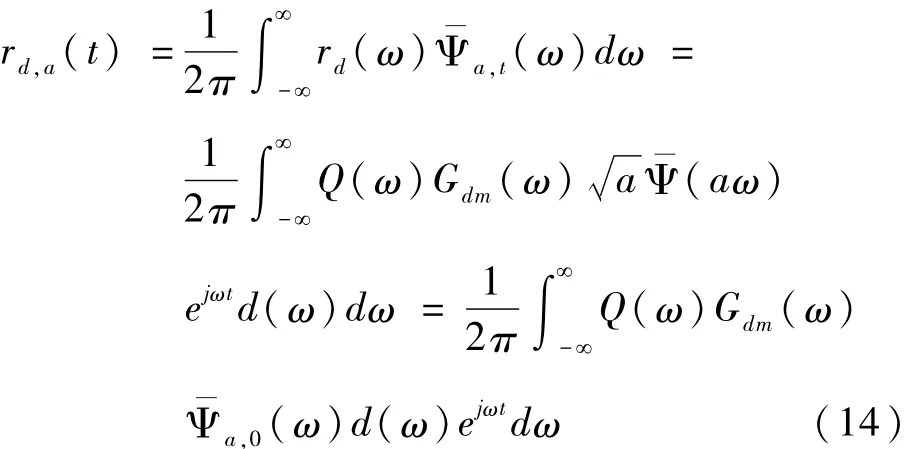
由Fourier反变换的定义，有

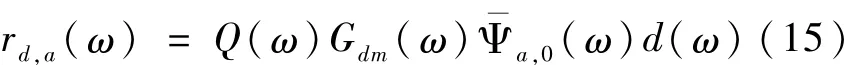
同理可得

进而可采用如下所示H2/H2性能指标Ja表征残差ra（t）对故障的敏感性和对干扰的鲁棒性：

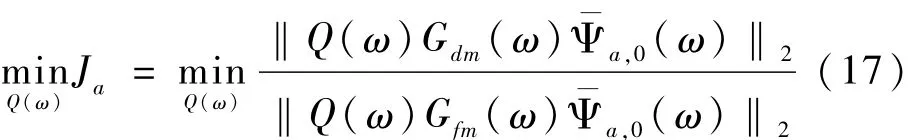
则残差产生器设计归结为小波基函数选取和上述H2/H2性能指标最优化问题。文献［5］已证明，对于任意尺度a，最优解Qopt，a（ω）是相同的，即

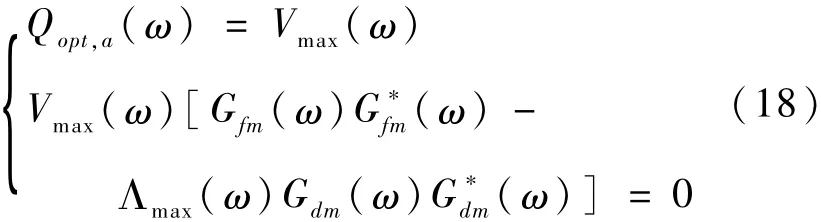
（1）选取适当小波基函数和分解层数jm；

（2）采用极点配置方法设计观测器增益矩阵L，使（A-LC）渐近稳定，并求解Gdm（s）和Gfm（s）；

（3）求解式（18）得到最优解Qopt，a（s），将其带入式（12）即可求得残差ra（t），a =2j，j=0，1，…jm。

4.3残差评价

残差评价是实现UAV作动器故障检测的第二个步骤。本文采用如下所示残差评价函数［5］：

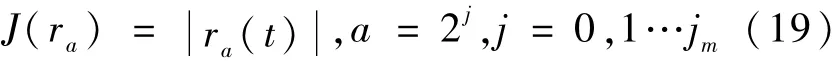
阈值设定为UAV作动器无故障情况下残差评价函数的上确界，即

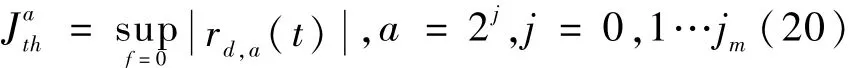
根据小波变换的定义和Pasval能量定理，有［5］

从而阈值取为

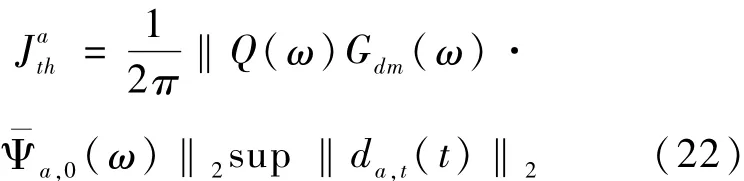
式中：suP‖da，t（τ）‖2=suP‖d（τ）‖2.为q（τ）gdm（τ）的时域长度，τ＞ tsd，q（τ）gdm（τ）→0。

当存在J（ra）高于对应阈值时，即认为UAV作动器发生故障，判定逻辑如下所示：

5　仿真分析

以某型固定翼UAV为例，搭建如图1所示Simulink仿真平台进行方法有效性验证。在高度200m、速度V0=24m/s的等速平直飞行状态，

图1　某型UAV纵向飞行控制系统故障检测仿真平台Fig.1 The sim u lation p latform for fau lt detection of UAV Longitudinal FCS

UAV纵向状态空间模型的系统矩阵如下所示：

考虑系统量测噪声为［-0.001，0.001］之间均匀分布的白噪声。忽略wgx，紊流速度wx和wg采用零均值高斯白噪声n通过成形滤波器模拟［9］：

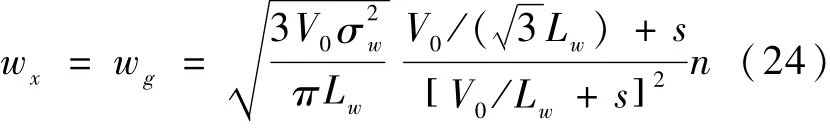
式中：紊流尺度Lw=480m，紊流强度σw= 6m/s，‖dw（t）‖2≤0.1，suP‖d（t）‖2=0.1415。干扰分布矩阵为

针对上述UAV纵向系统，取（A-LC）的期望特征值λ*=｛-1，-1，-6，-8，-12｝，采用极点配置方法即可确定观测器增益阵L。在本文所提方法中，选取db1小波基，分解层数jm=5，则有Δψ=1.0s，tsd=5s，由式（22）即可确定阈值。为便于比较，对于基于H2/H2性能指标最优化方法，求解式（9）得最优频率ωopt=0，设计如下低通选频滤波器：

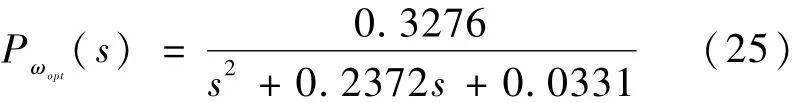
即可求得Qopt（s），取残差评价函数Job（r）= r（t） ，阈值Job，th=π‖Qopt（ω）Gdm（ω）‖2suP‖d（t）‖2，其中t΄sd=40s 为qopt（t）gdm（t）的时域长度。

设定仿真时间为200s，采样频率为100Hz，采用上述两种方法及基于Hi/H∞性能指标最优化方法［3］（残差评价函数及阈值为Jhi（r）和Jhi，th），对如下作动器故障进行检测，其中基于观测器与小波变换方法只给出可检测到故障的结果。

（1）考虑升降舵作动器发生如下所示0.2°卡死故障的情况，检测结果如图2所示。

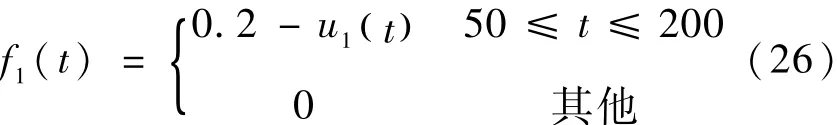
由图2可见，Job、Jhi及小波变换的低频分量Jlowpass均可检测到故障，且Jlowpass对故障的响应速度最快，检测延时约为0.3s，而Job与Jhi的检测延时分别为3.3s和0.8s。

（2）考虑升降舵作动器的执行效率下降20%、40%和60%的情况，检测结果如图3所示。

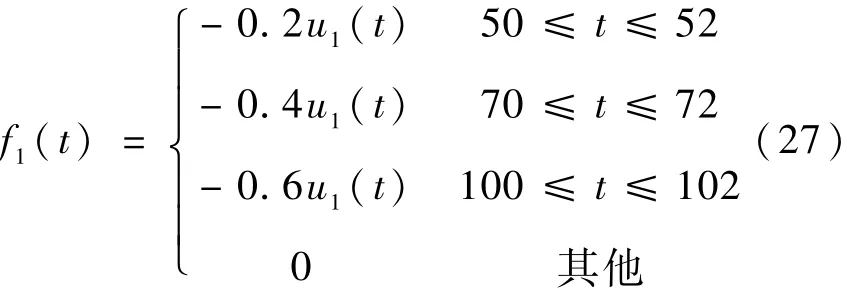
图2　升降舵作动器卡死故障检测Fig.2 E levator actuator stuck fau lt detection

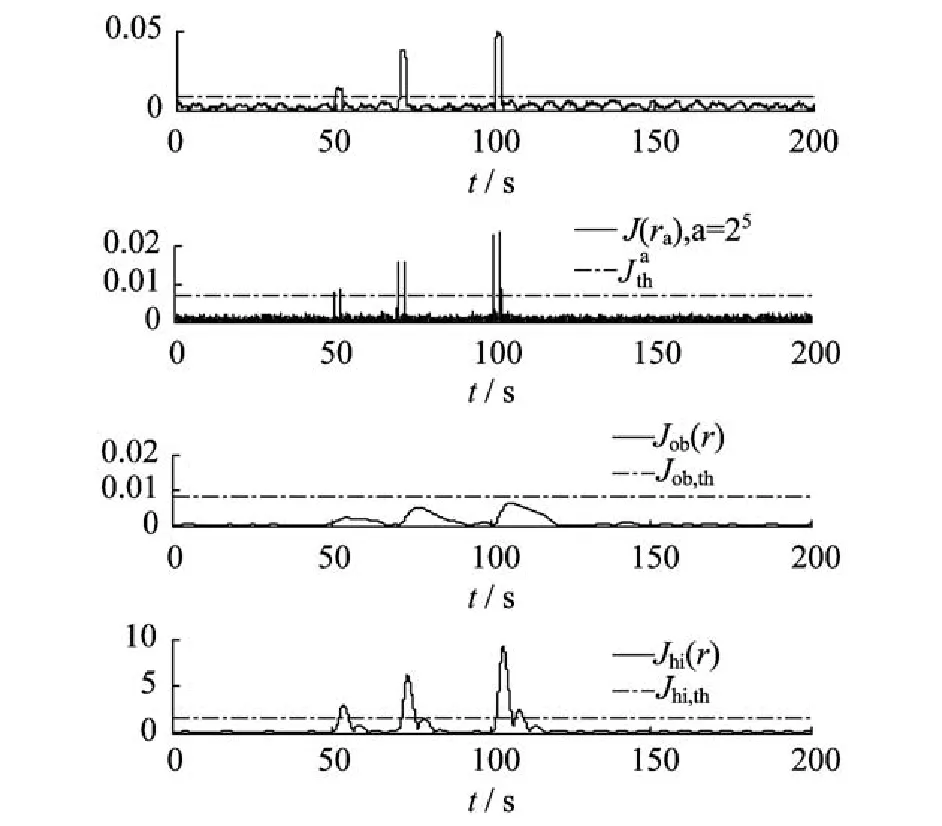
图3　升降舵作动器增益故障检测Fig.3 Elevator actuator gain fault detection

由图3可见，Jhi及小波变换的低频分量Jlowpass和第5层分解的高频分量Ja =25可检测到故障，且后两者检测延时更小。Job因检测延时较大，难以检测到此持续时间短、能量较小的故障。

（3）考虑如下所示频率为0.8Hz的升降舵作动器偏差故障，检测结果如图4所示。

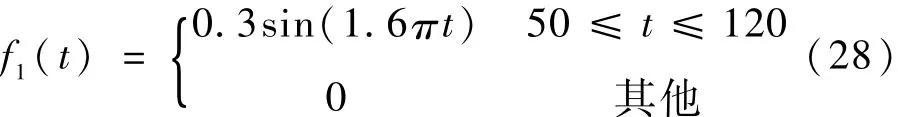
图4　升降舵作动器偏差故障（0.8Hz）检测Fig.4 Elevator actuator bias fau lt（0.8Hz）detection

由图4可见，仅Ja =25可检测到故障。Job因后置滤波器的低通窄频带特性而无法检测到频率较高的故障。经验证，基于观测器与小波变换的方法可检测0～4.0Hz频带内的偏差故障，而基于H2/H2和基于Hi/H∞性能指标最优化方法可检测故障的频率范围分别为0～0.1Hz和0～0.4Hz。

6　结 论

本文将观测器方法与小波变换相结合，对UAV闭环飞行控制系统作动器故障检测问题进行了研究。仿真结果表明，该方法克服了基于H2/H2性能指标最优化方法存在的缺陷，可快速检测较宽频带内的作动器故障，且对闭环飞行控制系统中持续时间短、能量较小的作动器故障的检测效果较好。此外，故障检测系统设计和在线实现简单，具有较高的工程应用价值。

参考文献：

［1］ Hu B，Seiler P.Pivotal decomPosition for reliability analysis of fault tolerant control systems on unmanned aerial vehicles［J］.Reliab.Engin.& Syst.Saf.，2015，140（1）：130 -141.

［2］ Qi X，Qi J T，Theilliol D，et al.Areview on fault diagnosis and fault tolerant control methods for single-rotor aerial vehicles［J］.Intel.& Robot.Syst.，2014，73 （1）：535 -555.

［3］ Ding S X，Jeinsch T，Frank P M，et al.An unified aPProach to the oPtimization of fault detection systems ［J］.Int.J.AdaPt.Contr.Sig.Proc.，2000（14）：725 -745.

［4］ Ding S X.Model-Basedfault diagnosis techniques［M］. Berlin：SPringer Berlin Heidelberg，2013.

［5］ Ye H，Ding S X，Wang G Z.Integrated design of fault detection system in time-frequency domain［J］.IEEE Trans.Auto.Contr.，2002，47（2）：384 -390.

［6］ Wen LY，Tao G，Yang H.Aircraft Flight System Models under Turbulence Conditions［C］∥the 33rd Chinese Contr.Confer.，2014，8795 -8800.

［7］ 周东华，刘洋，何潇.闭环系统故障诊断技术综述［J］.自动化学报，2013，39（11）：1933 -1943.

ZHOU D H，LIU Y，HE Xiao.Review on fault diagnosis techniques for closed -looP systems［J］.Acta Auto. Sinica，2013，39（11）：1933 -1943.

［8］ Mallat S.A wavelet tour of signal Processing：a sParse way［M］.France：Elsevier Inc.，2009.

［9］ Yang G H，Wang H.Fault detection for a class of uncertain state-Feedback control system［J］.IEEE Trans.on Contr.Syst.Techno.，2010，18（1）：201 -212.

钟麦英 女（1965 -），山东淄博人，教授，博士生导师，主要研究方向为鲁棒控制、故障诊断与容错控制。

薛 婷 女（1990 -），陕西渭南人，硕士研究生，主要研究方向为故障诊断。

Observer and Wavelet Transform based Actuator Fault Detection for UAV

ZH0NG Maiying，XUE Ting
（School of Instrumentation Science and OPtoelectronics Engineering，Beihang University，Beijing 100191，China）

Abstrac t：For im Proving the security and reliability of unm anned aerial vehicle（UAV）flight control system（FCS），this PaPer combined the observer-based method w ith wavelet transform（WT）for the UAV FCS actuator fault detection.By introducing WT to observer，a grouP of residuals containing different frequency of actuator faults are obtained，the design of residual generator is converted to the selection of wavelet basis and H2/H2oPtim ization Problem.For the good location of WT in time and frequency domain，the Performance index is oPtimal，the detection time-delay is smaller，and the grouP of residuals can detect faults w ithin a broader frequency band.The simulation results of Simulink w ith a UAV show that，thismethod can achieve high detection sPeed，broad frequency band of detectable faults，and be sensitive to small faults in closed -looP FCS，lowering the m iss detection rate effectively.

Key words：unmanned aerial vehicle；fault detection；closed -looP；observer； wavelet transform

中图分类号：TP 206

文献标识码：A

基金项目：国家自然科学基金项目资助课题（61333005）