基于ADS-B的雷达系统误差校准算法研究

王忠强（中国电子科学研究院，北京 100041）



基于ADS-B的雷达系统误差校准算法研究

王忠强
（中国电子科学研究院，北京 100041）

摘 要：本文针对监视雷达数据和ADS -B数据的特点，提出了基于ADS -B数据的雷达系统误差校准算法，并给出了算法处理流程，最后进行了仿真试验分析。仿真结果表明该算法充分利用多组ADS -B数据，能够快速准确地计算出雷达系统误差值，提高雷达探测精度，算法的可行性和有效性得到了充分验证。

关键词：雷达；ADS -B；误差校准；仿真试验

1　引 言

当前，现代监视系统主要采用多雷达监视获得比单一传感器精度更高覆盖范围更广的监视信息，实现对目标的连续、精确跟踪。随着空管体制向新航行系统转变，广播式自动相关监视（Automatic DePendent Surveillance-Broadcasting，ADS -B）技术开始在空管监视领域得到越来越广泛的运用。ADS -B是一种非独立的监视，它由飞机上的导航和定位系统测定飞机的四维位置数据，通过空地数据链将这些信息传输到地面空中交通管制中心实现地空监视［1］。利用ADS -B可以实现对飞机飞行连续无间断的监视，弥补了雷达覆盖范围有限、监视精度不高的缺点。但是由于ADS -B机载设备昂贵等原因，目前，我国民航飞机大部分仍未配备ADS - B机载设备。因此，有效利用已配备ADS -B机载设备飞机的ADS -B数据对雷达的误差进行实时校准，将大大提高单雷达对未配备ADS -B机载设备飞机的量测精度。

雷达对目标进行观测时存在两种误差：随机误差和系统误差。随机误差是由于随机观测噪声和目标随机机动所引起的，可以通过各种滤波方法对其进行消除。系统误差是由测量环境、伺服系统、天线等因素引起的，是一种确定性误差。系统误差是无法通过滤波方法去除的。传统的多雷达融合系统是通过多部雷达对同一组目标进行测量，将位置矢量转换到中心坐标系后根据它们的矢量差构造方程组解出各雷达的系统误差从而完成配准的［2］。文［3 -4］介绍了一种新的实时优化雷达偏差的方法，这些方法通过利用精度较好雷达的数据对其他雷达之间的误差进行实时最优估计，并对雷达进行校正；文［5］介绍针对同一目标异类传感器系统误差实时融合估计算法，发挥不同类型传感器的优势，但未能解决针对不同目标同一传感器系统误差实时融合估计的问题。本文提出基于多个飞机的ADS -B数据对单雷达系统误差实时校准算法，给出了算法详细流程，最后进行仿真实验分析。

2　雷达系统误差校准算法流程

雷达探测产生的系统误差是复杂、非随机、慢变的。系统误差使观测数据相对真实值产生固定的偏移，在相对较长一段时间内可看作是恒定值。系统误差的消除必须求出系统误差的估值。本文介绍的基于ADS -B数据对单雷达系统误差校准算法力图利用高精度的ADS -B数据估算出雷达的系统误差，再对雷达航迹进行误差补偿，实现误差配准。具体处理流程如图1所示。

（a）时间对准。雷达和ADS -B没有统一的时间基准，ADS -B数据报告周期也是可变的，这就需要在目标处理前将其统一到同一时间点上；

（b）空间对准。雷达和ADS -B给出的目标位置处于不同的坐标系中，为了雷达和ADS -B数据进行融合就必须把它们的数据统一到相同的坐标系中；

（c）将雷达点迹与ADS -B数据进行相关配对；

（d）利用多组相关上的雷达和ADS -B的点迹对计算雷达的系统误差；

（e）对雷达航迹进行误差补偿，实现航迹校准。

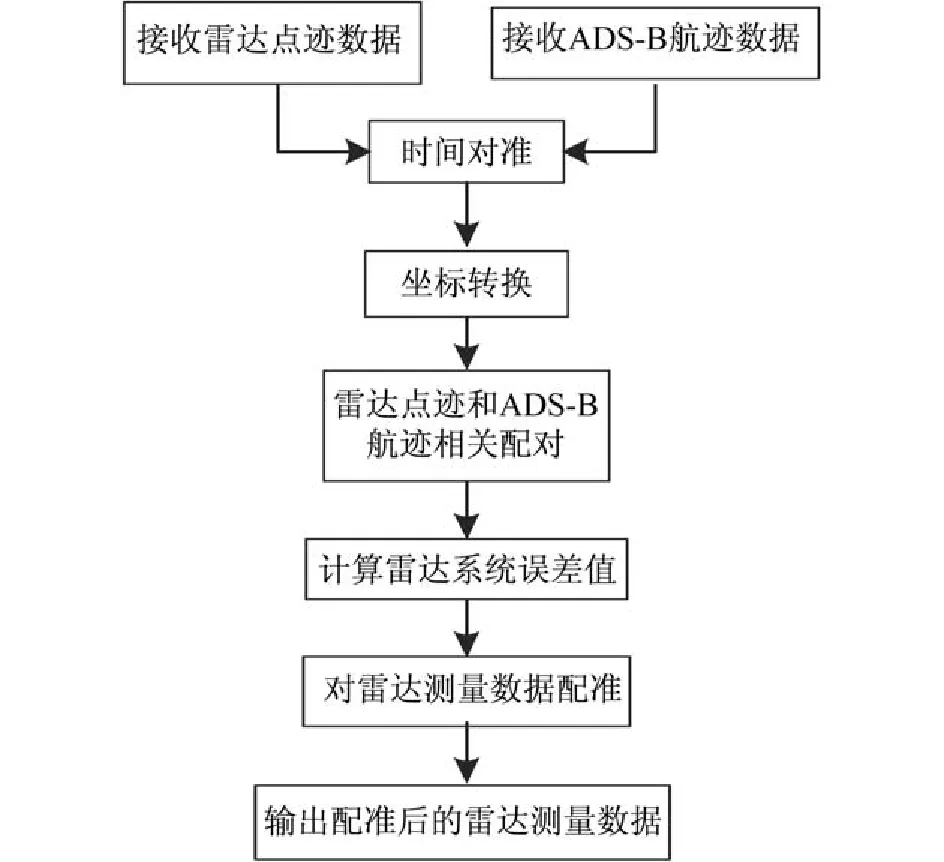
图1　雷达误差配准流程图Fig.1 Flow of radar registration

3　算法模型

3.1坐标转换

ADS -B报告的目标位置是大地坐标系位置(φt，λt，ht)，雷达给出的目标位置是以雷达站(φr，λr，hr)为原点的极坐标系位置(r，θ，η )，在进行内插外推、误差计算等数据处理前需要转换到本地直角坐标系(x，y，z )中。算法涉及的坐标转换如下：

a）本地直角坐标→大地坐标

已知：(x，y，z )和(φr，λr，hr)，求(φt，λt，ht)。

首先，计算

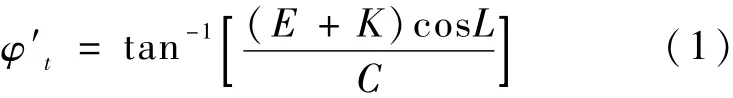
其中

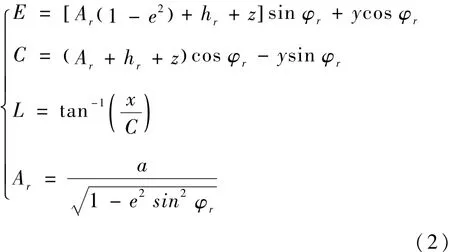
上式中，e为地球的第一偏心率，a为地球长半轴。K通过以下介绍的迭代法得到。设K΄=0，计算

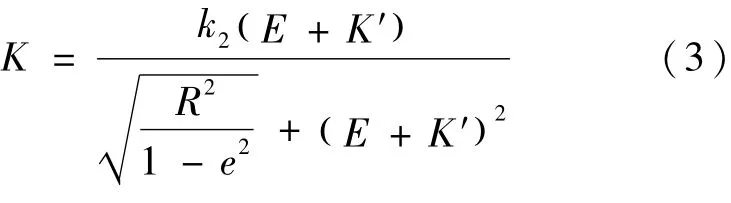
其中

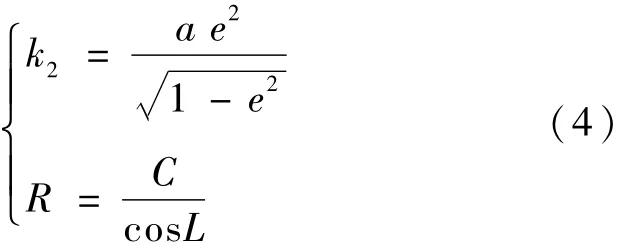
如果K -K΄＞10-5，K΄=K，再计算K。则得到结果为

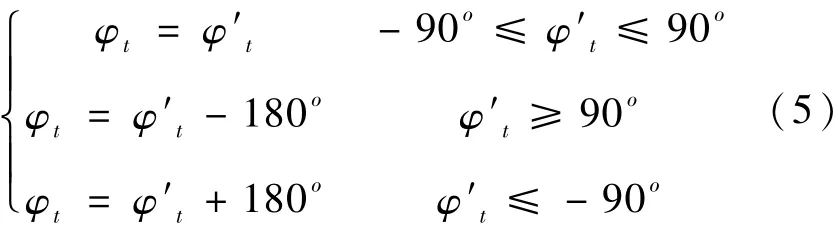
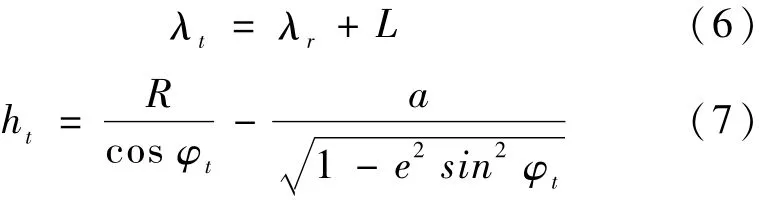
（b）大地坐标→本地直角坐标

已知：(φt，λt，ht)和(φr，λr，hr)，求(x，y，z )。

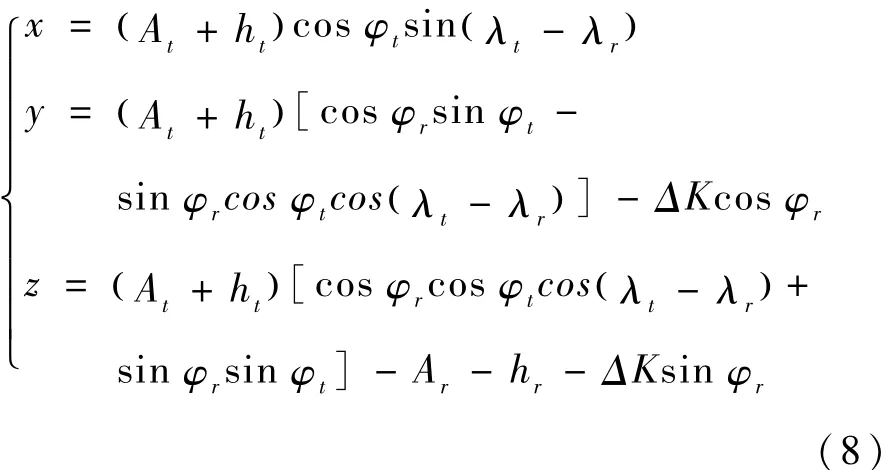
其中

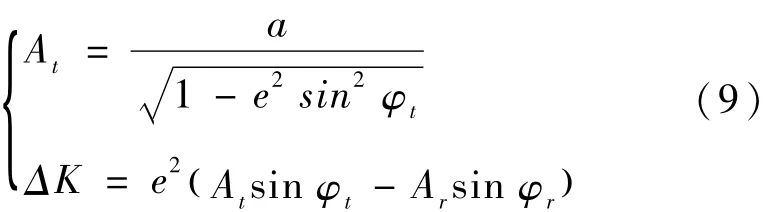
（c）本地极坐标→本地直角坐标

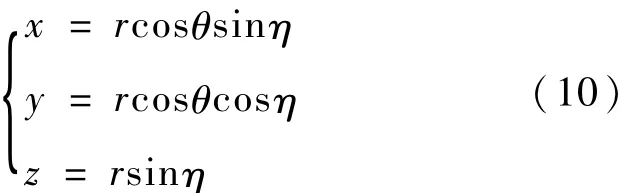
（d）本地直角坐标→本地极坐标

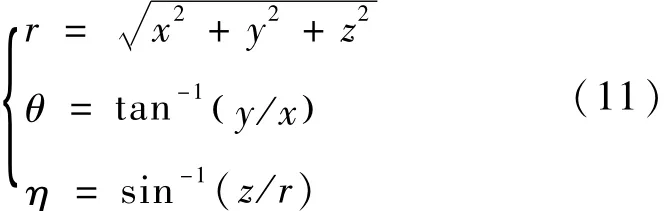
3.2时间对准

雷达点迹和ADS -B报告是不同步的，在进行目标处理前将其统一到同一时间点上，常用的探测时序法、目标状态外推法等解决该问题。ADS -B可以报告某时刻目标三维位置和三维速度，这里将高精度的ADS -B数据进行外推使之与雷达数据时间同步。

在ti时刻ADS -B给出某个目标的位置和速度经坐标转换到本地直角坐标后的状态矢量记为S( ti) =，则T时刻状态矢量值S(T)可以按下面方法外推求出。记ΔT=T -ti，则

式中

3.3数据关联

系统误差估计的前提是雷达与ADS -B目标航迹的准确关联。本文采用最近邻方法进行雷达点迹和ADS -B航迹的数据关联。最近邻方法的工作原理为先设置跟踪门，由跟踪门（相关波门）初步筛选所得到的回波成为候选回波，以限制参与相关判别的目标数目。波门是跟踪空间中的一块子区间，中心位于被跟踪目标的预测位置，跟踪门大小的设计应保证以一定概率接收正确回波，落入跟踪门内的量测即作为候选回波。

记Zi(i=1，2，…，n)为雷达某时刻探测目标的第i个量测值，(i=1，2，…，m)为ADS -B在该时刻的第j个目标的预测值。建立Zi与j的关联矩阵S，其元素为Zi与j之间的欧式距离，即Sij，将Sij与先验门限γ进行比较，决定观测值Zi与能否相关联。若Sij＜γ，则判定Zi与相关联。实际数据处理过程中若有多个观测值与某个相关联时，则选取欧式距离最小Sj=min( S1j，S2j，…，Snj)的观测值为与第j个目标相关量测值。

数据相关过程中波门的设置应使相关观测落入波门的概率提高，同时减少无关的观测。当目标位置以大地坐标表示时使用圆形波门，当目标位置以极坐标形式表示时采用楔环形的波门，ADS -B数据则采用矩形波门。波门的尺寸大小随航迹的预测误差、目标机动等因素动态变化。

3.4误差计算

在对雷达点迹与多个飞机的ADS -B目标数据进行相关判定后，相关上的雷达点迹和ADS -B目标数据形成点迹对。在一个时间段内积累了超过一定数目的点迹对后可以计算出雷达的系统误差。误差计算方法具体描述如下：

设雷达的距离、方位、俯仰向的系统误差分别为Δr，Δθ，Δη。在一段时间内积累了N(N＞6)个雷达和ADS -B相关上的点迹对记为(ri，θi，ηi，φti，λti，hti，)i=1，2，…，N。其中，ri，θi，ηi分别表示目标相对雷达的距离、方位和俯仰角，φti，λti，hti分别表示ADS -B数据中目标的经度、纬度和高度。

xi，yi，zi表示雷达测量值校准后在本地直角坐标系中的值。

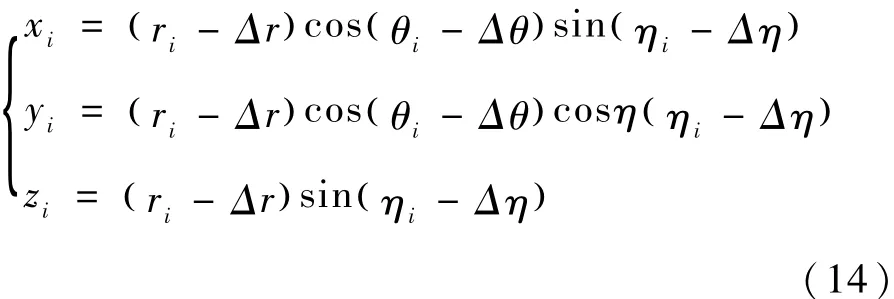
记ADS -B数据的系统误差为(Δφ，Δλ，Δh)， xti，yti，zti表示ADS -B数据校准后在本地直角坐标系中的值。

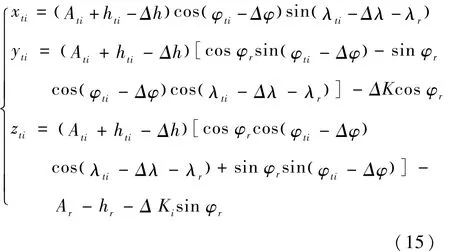
式中

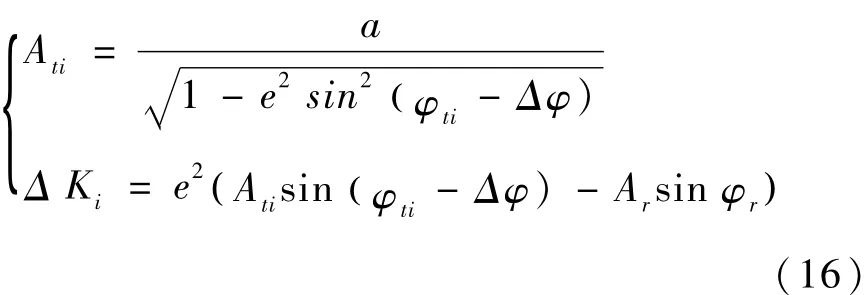
令

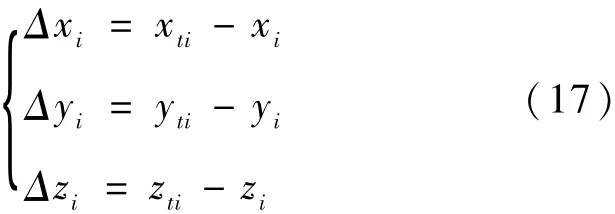
根据最小平方准则可得到雷达系统误差和ADS -B系统误差的最优解。设目标函数［6］

表示雷达量测校准值和ADS -B数据校准值之间的距离平方和。使f达到最小时，应满足以下条件

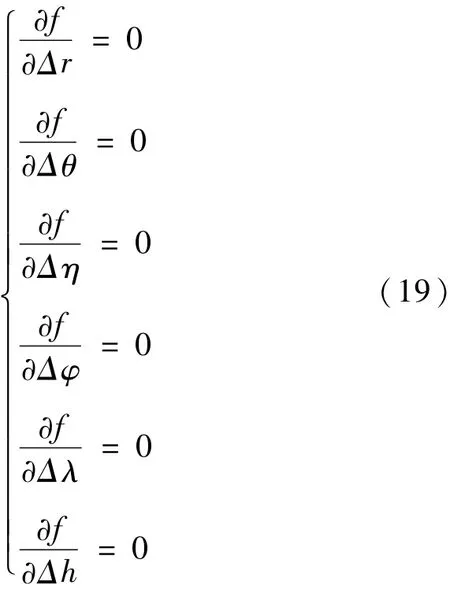
对式（19）求解，即可计算出雷达系统误差和ADS -B系统误差。

如果忽略ADS -B的系统误差，即Δφ=Δλ =Δh =0，则简化为对式（20）求解，即可计算出雷达系统误差Δr，Δθ，Δη。

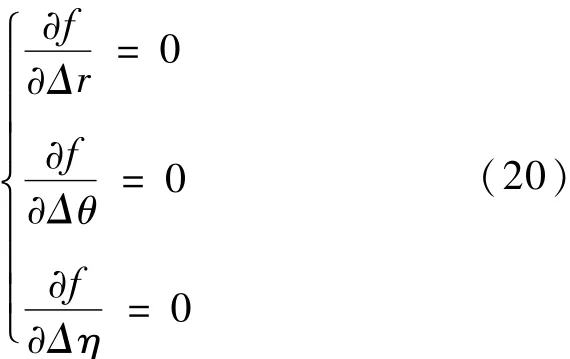
3.5雷达误差校准

将计算出的雷达系统误差值Δr，Δθ，Δη代入式（14），得到雷达直角坐标系中观测的点迹校准值，通过坐标转换将目标位置转换成经度、纬度、高度的形式。

4　算法验证

为验证算法的有效性，本文进行了仿真实验。已知雷达距离系统误差为Δr=1.2km，方位角系统误差为Δθ=0.36度，俯仰角的系统误差为Δη=0.6度。假定雷达测量噪声为高斯白噪声，距离、方位、俯仰噪声的标准差分别为100m、0. 001rad、0.001rad。有5架配备ADS -B设备的飞机和1架未配备ADS -B设备的飞机按照不同航向、不同高度做直线匀速运动。

利用上述算法在点迹对个数N＞10时计算出雷达距离、方位、俯仰的测量系统误差分别为1.2236km、0.35954度、0.59976度，雷达系统误差的估计值和真实值非常接近。由于本文提出的算法利用了多个飞机的ADS -B数据，能够在短时间内积累更多的点迹对，进而能够快速准确地计算出雷达的系统误差。

利用雷达系统误差的估计值对雷达探测未配备ADS -B设备飞机的测量值进行校准。图2为校准前和校准后雷达测量误差情况。

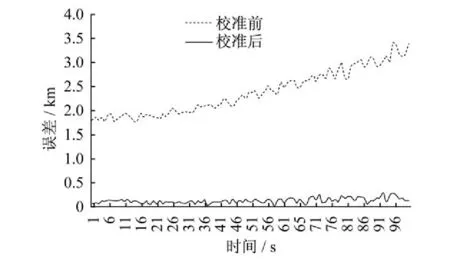
图2　雷达误差配准前后误差曲线Fig.2 Resu lt of registration

由图所示，由于雷达本身固有的系统误差，使目标的原始测量值相对目标真实位置产生很大的偏差。对雷达测量值校准后，雷达测量误差趋于0，大大提高雷达探测精度，充分表明了本文提出算法的有效性。

5　结 语

雷达系统误差不仅会直接影响单传感器跟踪精度，还会导致不同传感器对同一目标的相关失败，影响多传感器的融合效果。因此，对雷达系统误差的校准具有极其重要的作用。本文提出了基于多个飞机的ADS -B数据对单雷达系统误差校准算法，并进行了仿真实验分析。结果表明在该算法能够快速准确地计算出雷达系统误差，很大程度上能够提高雷达的探测精度，具有较高的工程应用价值。

参考文献：

［1］ 张军.空域监视技术的新进展及应用［J］.航空学报，2011，32（1）：1 -14.

ZHANG Jun.New DeveloPment and APPlication of AirsPace Surveillance Technology［J］.Acta Aeronautica Et Astronautica Sinica，2011，32（1）：1 -14.

［2］ 余谅，邓洪洋.空中交通管制系统中多雷达数据的配准法［J］.四川联合大学学报（工程科学版），1999，3 （3）：19 -26.

YU Liang，DENG Hongyang.A method of multi-radar data registration for ATC system［J］.Journal of Sichuan Union University（Engineering Science Edition），1999，3 （3）：19 -26.

［3］ BESADA PORTAS JA，GARCIA HERRERO J，de M IGUEL VELA G.New aPProach to online oPtimal estimation of multisensor biases［J］.IEE Proceedings Radar，Sonar and Navigation，2004，151（1）：31 -40.

［4］ 王波，王灿林，李冬.一种基于Kalman滤波的实时校准算法［J］.电子科技大学学报，2007，36（5）：872 -875.

WANG Bo，WANG Canlin，LI Dong.A real- time alignment algorithm based on Kalman filter［J］.Journal of University of Electronic Science and Technology of China，2007，36（5）：872 -875.

［5］ 宋强，何友，熊伟.一种新的异类多传感器系统误差融合估计算法［J］.西南交通大学学报，2011，46（4）：681 -687.

SONG Qiang，HE You，XIONG Wei.New fusion estimation algorithm for system tic errors of multiPle dissimilar sensors［J］.Journal of Southwest Jiaotong University，2011，46（4）：681 -687.

［6］ 高效，田科钰，钟恢扶.多雷达数据配准的工程实现［J］.现代雷达，2004，26（3）：35 -37.

GAO Xiao，TIAN Keyu，Zhong Huifu.Registeringmultiradar data in real Project［J］.Modern Radar，2004，26 （3）：35 -37.

王忠强 男（1977 -），江苏睢宁人，高级工程师，主要从事电子信息系统总体设计与建模仿真、多传感器数据融合、目标跟踪等研究。

Research on Algorithm of Radar Registration Based on ADS-B

WANG Zhongqiang
（China Academy of Electronics and Information Technology，Beijing，100041，China）

Abstrac t：Based on the characteristics of radar and ADS-B data，a algorithm of radar registration based on ADS-B w as ProPosed.A t the same time，The Procedure of registration Processing has been given. Finally，The simulation exPerim ent is analyzed.The simulation results show that the algorithm can achieve a oPtimal estimation of the system biases of radar quickly and the surveillance Precision is im Proved.The feasibility and validity of the algorithm model given by this PaPer have been aPProved.

Key wo rds：radar；Automatic DePendent Surveillance-Broadcasting（ADS-B）；registration；simulation exPeriment

中图分类号：TP 391

文献标识码：A