找准分类标准，解题不重不漏

李秀真

分类讨论是一种重要的数学思想方法，也是一种重要的解题策略. 当问题所给的对象不能进行统一研究时，就需要对研究对象进行分类，然后对每一类分别研究，给出每一类的结果，最终综合各类结果得到整个问题的解答. 分类必须从同一标准出发，做到不重复，不遗漏，包含各种情况.下面结合两道中考压轴题讲解分类讨论思想.

例1 （2015·南通）已知抛物线y=x2-2mx+m2+m-1（m是常数）的顶点为P，直线l：y=x-1.

（1） 求证：点P在直线l上；

（2） 当m=-3时，抛物线与x轴交于A，B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图1），求点M的坐标；

（3） 若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的m的值.

【思路突破】（1） 利用配方法得到y=（x-m）2+m-1，点P（m，m-1），然后判断点P是否在直线l上即可；

（2） 先确定抛物线解析式，根据抛物线与x轴、y轴的交点求出A、B、C三点的坐标，再通过解方程组求得Q、P点的坐标，然后分别过点P、点M作x轴和y轴的垂线构造两个直角三角形，利用相似的性质得到M点的坐标；

（3） 通过解方程组得到点M、Q两点的坐标，再利用两点间的距离公式得到三角形三边PQ、OQ和OP的长，在三角形中只要有两边相等就可以判断该三角形是等腰三角形，所以要对三种情况进行分类讨论：当PQ=OQ时，当PQ=OP时，当OP=OQ时，最后分别解关于m的方程求出m即可.

【解答】（1） 证明：

∵y=x2-2mx+m2+m-1

=（x-m）2+m-1，

∴点P的坐标为（m，m-1），

∵当x=m时，y=x-1=m-1，

∴点P在直线l上.

（2） 当m=-3时，抛物线解析式为y=x2+6x+5.

当y=0时，x2+6x+5=0，解得x1=-1，x2=-5，

则A（-5，0），B（-1，0）；

当x=0时，y=5，则C（0，5）.

联立方程组y=x2+6x+5，y=x-1.

解之得x=-3，y=-4，或x=-2，y=-3.

∵P（-3，-4），∴Q（-2，-3）.

过点M作ME⊥y轴于点E，过点P作PF⊥x轴于点F，过点Q作QG⊥x轴于点G，如图2所示，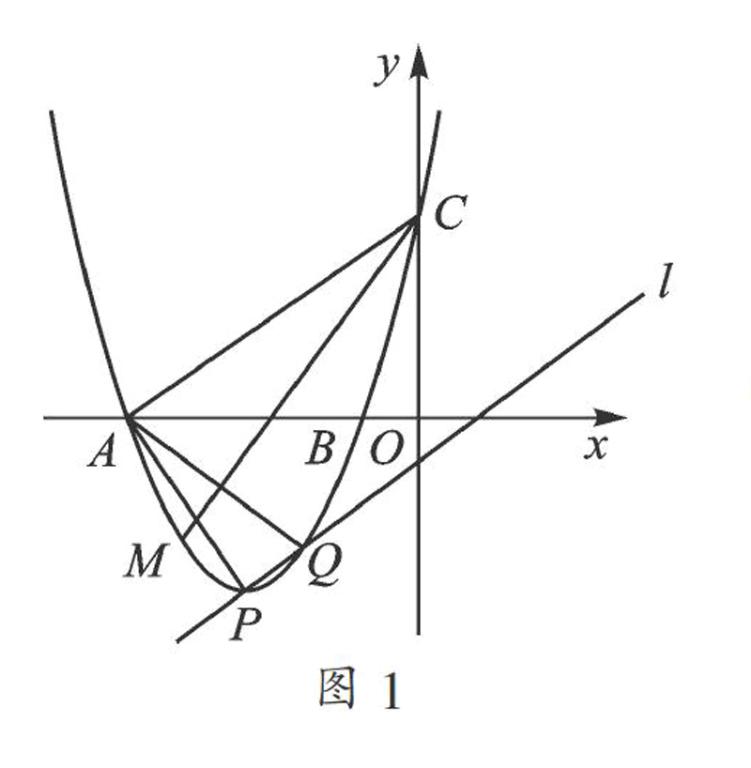

整理得x2+4x=0，

解之得x1=0（舍去），x2=-4，

∴点M的坐标为（-4，-3）.

（3） 联立方程组y=x2-2mx+m2+m-1，y=x-1，

解得x=m+1，y=m，或x=m，y=m-1，

则P（m，m-1），Q（m+1，m），

∴PQ2=（m+1-m）2+（m-m+1）2=2，

OQ2=（m+1）2+m2=2m2+2m+1，

OP2=m2+（m-1）2=2m2-2m+1.

①当PQ=OQ时，2m2+2m+1=2，

解之得m=；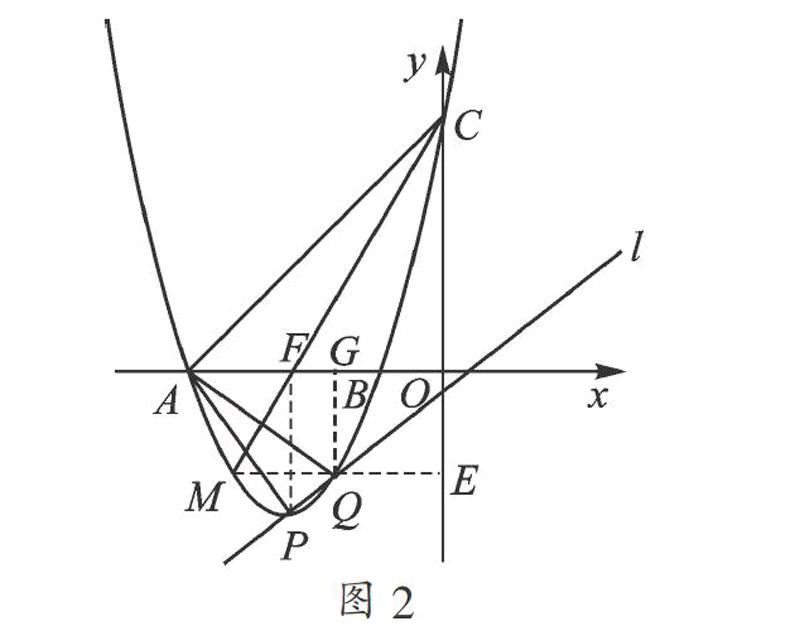

②当PQ=OP时，2m2-2m+1=2，

解之得m=；

③当OP=OQ时，

2m2+2m+1=2m2-2m+1，解得m=0.

综上所述，m的值为0、时，△OPQ是等腰三角形.

【解后反思】此题属于二次函数综合题，涉及的知识点有：二次函数图像和一次函数图像上点的坐标特征，二次函数性质，两点间的距离计算，利用相似比计算线段长等，遇到等腰就想到分类讨论思想是本题解答关键.

例2 （2015·泰州）已知一次函数y=2x-4的图像与x轴、y轴分别相交于点A、B，点P在该函数图像上，P到x轴、y轴的距离分别为d1、d2.

（1） 当P为线段AB的中点时，求d1+d2的值；

（2） 直接写出d1+d2的范围，并求当d1+d2=3时点P的坐标；

（3） 若在线段AB上存在无数个P点，使d1+ad2=4（a为常数），求a的值.

【思路突破】（1） 由一次函数解析式求出A与B的坐标继而求出AB的中点P的坐标；

（2） 设P（m，2m-4），表示出d1+d2，分类讨论m的范围，根据d1+d2=3求出m的值；

（3） 设P（m，2m-4），利用绝对值的代数意义表示出d1与d2，代入d1+ad2=4，根据存在无数个点P求出a的值即可.

【解答】（1） A（2，0）、B（0，-4），P为AB的中点，

【解后反思】此题属于一次函数综合题，涉及的知识点有：一次函数与坐标轴的交点，线段中点坐标公式，绝对值的代数意义以及坐标与图形性质.熟练掌握绝对值的代数意义是解本题的关键.