社团结构网络环境下SIS病毒传播建模与分析

李婵婵，蒋国平

(南京邮电大学 a.计算机学院；b.自动化学院,南京 210003)



社团结构网络环境下SIS病毒传播建模与分析

李婵婵a，蒋国平b

(南京邮电大学 a.计算机学院；b.自动化学院,南京 210003)

摘要:考虑许多现实网络具有社团结构，通过引入模块化系数，并在该系数合理范围控制下基于随机网络生成社团网络模型以模拟现实社会网络。通过平均场方法研究网络上的病毒传播动力学行为，推导传播阈值表达式，并用蒙特卡罗仿真加以验证。研究表明：社团结构的存在使得网络度分布发生变化，即社团结构越强，度分布越宽；同时，社团结构越强，病毒越易爆发；另外，传染率远大于阈值时，不同强度的社团结构网络的传播规模趋于一致，即网络结构对传播规模影响不大。

关键词：复杂网络;社团结构;病毒传播;平均场

0引言

传染病的流行，病毒在计算机网络上的传播以及谣言在信息网络中的蔓延，对经济社会的发展带来巨大冲击。因此，研究病毒的传播机理进而采取相应措施，有效应对和控制病毒的传播，具有重要的研究价值和现实意义。一方面，生物系统、通讯系统、网络媒介等，甚至宏观的经济运行、社会管理等，都可以通过复杂网络来描述；另一方面，复杂网络理论的快速发展，为人们理解病毒的传播机理和防控病毒的扩散蔓延，提供了新起点、新方法。近年来，借助于复杂网络理论研究病毒、谣言等的传播动力学[1-7]正在引起学者们的关注。正是由于社会网络与人们正常生活的高度相关性，使得社会网络中的病毒传播日益成为学术界关注的热点。

人们很早就提出了多种流行病传播模型。根据个体在系统中所处状态，通常将相关个体抽象为易感个体、感染个体、免疫个体等等，并依据个体状态的转换过程来命名传染病模型，SI模型、SIS模型和SIR模型是其中的3个经典模型。SI模型中，易感个体被感染后无法恢复健康；在SIS模型中，易感个体感染后以一定概率恢复健康，并可能再次被感染；在SIR模型中，易感个体被感染后恢复健康且具有免疫力，不会再被感染。

作为定量理论研究的一种重要方法，传染病动力学建模在病毒传播领域得到广泛应用，也被引入到针对社会网络的统计特性及病毒传播研究之中，且取得了积极进展[8-11]，其中一个重要发现是：社会网络具有社团结构特性[8]。进而，一些学者通过构建社团结构网络模型模拟现实网络，推进病毒传播动力学的研究[12-22]。

文献[12-16]基于不同病毒传播模型，研究无标度社团网络中的传播特性，研究表明：社团结构抑制了病毒传播。文献[16]研究了异质社团网络中流行病传播的可预测性问题，发现：桥节点度越小或传染源离桥节点越远，传播的可预测性越好；强社区结构虽然的确能够阻碍病毒扩散，但却易于导致传播的不可预测性，而避免桥节点的感染是提高传播可预测性的关键。文献[17-18]考虑含有权重的无标度社团网络中的病毒传播动力学，其中[18]对比研究了紧耦合-小权重和松耦合-大权重这两种混合型社团结构网络模型(具有相同模块化系数)对病毒传播的影响。文献[19]考虑了重叠社团结构网络上的病毒传播，得到社团结构重叠部分增大会导致传播规模增大的结论。文献[20]则基于随机网络构建社团结构网络并定义了一个参量来表征社团化程度，研究社团结构对传播动力学的影响，发现社团化程度越大，传播阈值越小，病毒越容易爆发。文献[21]基于传统SIS和交通流驱动SIS病毒模型，在随机社团结构网络中研究了社团结构对病毒传播速度的影响，发现：随着社团化程度的增大，在传统SIS模型中传播速度受到抑制，而交通流驱动SIS模型反之。文献[22]构建了含有两个不同度分布随机网络的社团网络，仿真结果表明度分布较大的社团会持续处于地方病状态，而病毒在度分布较小的社团内会爆发和灭绝交替发生。文献[23]将真实网络中的连边分为确定性连边和随机性连边，通过频谱分析发现：根据确定性连边信息和随机连边的生成概率就可以预测病毒传播阈值范围；并基于小世界网络构造具有确定连边和随机性连边的异质社团结构网络，分析了不同社团规模下的传播阈值。另外，关于多种群网络、相互依赖和相互连接复杂网络上的病毒传播[6,24-26]也类似于社团结构网络上的传播动力学。

本文在文献[20]的基础上，引入模块化系数来判定网络模型是否符合实际网络；运用平均场方法建立社团网络环境下的SIS病毒传播模型，推导出流行病传播阈值的准确表达式，研究病毒传播的动力学，并采用蒙特卡罗仿真加以验证。

1社团结构网络模型

1.1网络模型

社团网络模型的生成过程为：1)网络中总节点数为N，分为m组社团，各组分别有ni(i=1，2，…，m)个节点，为更真实反映现实社会网络，一般设各个社团的规模不同；2)各社团内的任意一对非邻节点以概率α相连；3)任意两个社团之间的非邻节点以概率β相连。

一般在社团内部，节点间紧密连接，而社团间连边较少，因此α≫β。任意一个社团i内部连边数为ni(ni-1)α/2，任意两个社团i，j间含有ninjβ个社团间连边，则网络中连边总数K为

(1)

文献[20]中定义了一个参量：群落化程度ε(ε=α/β)用以表征网络模块化程度以及确定α,β的大小：当ε=1时，网络为随机网络；当ε≫1时，则生成社团结构网络，同时，ε越大，社团结构越明显。然而ε的取值是人为定义的，因此有必要确定ε的取值规则并使生成的网络模型与现实网络情形相符。结合Newman和Girvan在2004年提出的模块化系数[27]，找出ε与模块化系数Q之间的关系，从而可以确定ε的取值规则。模块化系数Q定义为

(2)

其中，

eii=ni(ni-1)α/2K

(3)

(4)

eii为社团i内部连边数占网络总连边数的比例，eij为社团i，j间的连边占网络总连边数的比例。本文在文献[20]的网络模型基础上，引入模块化系数Q，作为网络的社团化强度的衡量标准，并给出原文中ε的选取范围。

将式(3)、(4)代入式(2)中，得到模块化系数表达式：

(5)

由式(1)可以得到：

(6)

将式(6)带入式(5)中，得到关于β的一元二次方程：

(7)

分别令：

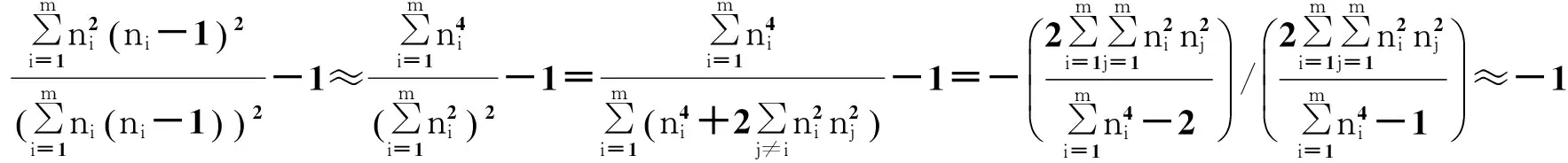
(8)

将式(8)带入式(6)中可以得到社团内连边生成率：

(9)

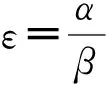
(10)

式(10)中A同上文。从式(10)可以看出Q与ε正相关。

图1表示Q与ε的关系曲线。实线(MF)为根据式(10)得到的理论值曲线，圆圈、三角以及菱形线(MC)为通过仿真得到的值，其中，3个子图的网络总边数K分别为5 000、10 000和25 000。在各子图中，Q与ε一一对应，且Q随着ε单调增大；通过对比3个子图发现网络连边数K对ε几乎没有影响。研究者们通过对多个具有社团结构特性的真实网络进行验证统计，发现一般网络的模块化系数Q((0.3,0.8)[21]，为保证Q的取值在此范围内，根据式(10)可推算出ε的取值范围ε((1,230)。

1.2网络度分布

图2反映了社团结构对网络度分布的影响。选取Q=0.3，0.5和0.7，并生成相应的网络，分别代表弱社团结构网络、中等强度社团结构网络以及强社团结构网络。从图上可看出，社团结构网络的度分布依然呈泊松分布，且随着Q的增大，网络度分布变宽，峰值变小。当Q=0.1时，网络的社团化强度更弱，度分布也是均匀的，只是度分布的峰值较Q=0.3时更高，且度分布的广度更小；同理，Q=0.9时，网络的社团化强度更强，度分布的峰值较Q=0.7时更低，且度分布的更广。所用参数为：N=1 000，K=25 000，m=10。通过随机生成500个网络，求出各网络的度分布并取平均值得到图中曲线。

图3给出节点对应的度值曲线。横坐标n表示节点编号，纵坐标k表示节点度，图中虚线用以区分社团。为了直观对比3个模块化系数的结果，固定n1=n2=…=n10=100，其他参数同上。从图中可知：节点的度值在k=50附近振荡变化，Q越大，振幅越大，这与图2中的Q越大，度分布越广相对应。这是由于各个社团内部分节点与其他社团有连边，所以社团内一部分节点的度较大，当Q越大，外部连边越少，社团内节点度的大小差异也越大。

2病毒传播模型及阈值分析

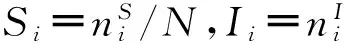
(11)

(12)

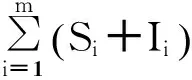
当网络的社团结构强度较大时，由于社团间连边很少，各个社团内部近似为随机网络，整个网络近似为均匀网络，如图2中Q=0.7所对应曲线；社团结构不强时，β越大(β无限趋近于α)，网络越接近于随机网络，网络基本还会保持度均匀性，如图2中Q=0.3对应的曲线。设初始时刻网络中有一个感染节点，当传播过程到达稳态时，由于网络参数相同，各社团内感染情况基本一致。为了简化计算，假设各个社团规模接近，则：

(13)

将式(13)代入式(12)得到：

(14)

令式(14)左边等于0，即可推导网络传播阈值：

qc=mγ/(α+β(m-1))

(15)

将式(8)、(9)中α、β代入式(15)，则得到传播阈值准确表达式：

(16)

前文中已知A>0，C<0，由式(16)可知qc与C负相关，且C正相关于Q，所以传播阈值qc负相关于模块化系数Q。

3仿真结果

3.1感染规模随时间的变化

图4表示在一定传染率下，感染规模随时间的变化曲线I(t)。实线、虚线以及点划线分别代表不同模块化系数，3个子图对应的连边总数分别为5 000，10 000和25 000。初始时刻网络中有一个种子节点，其它参数为N=1000，γ=0.5，m=10，循环次数为200。

从图4观察发现：在传播过程初期，较大Q值对应的感染节点增长速度较快；而到某一时间步，感染节点增长速度发生反转；且Q越大，到达传播稳态规模所用时间越长。以图4a为例，在t=17前，点划线对应的值最大，其次是虚线，最后是实线；t>17时，3条曲线的值大小反了过来，最终，3条曲线达到稳定，且稳定值基本一致，图4b、c也类似。由于网络中存在社团结构，社团间连边较少，在传播初期，病毒首先在社团内快速传播开来，社团内连边密度越大，传播速度越快，因此该时段内Q越大，传播规模增长也较快；而随着传播过程的发展，病毒也会通过外部连边进入其他社团，从而扩展到整个网络，外部连边越多，病毒扩散到全局网络的速度相对也越快，到达稳态所用时间也越少。模块化系数Q的大小只会影响传播速度和到达稳态所用时间，对传播规模影响不大。

3.2传播阈值仿真

根据式(16)分析得出传播阈值qc与模块化系数Q反相关。为了验证社团结构对传播阈值的影响，图5给出模块化系数Q=0.3,0.5和0.7时，对应的感染规模I与传染率q之间的关系图，网络总连边数K分别为5 000,10 000及25 000，初始时刻网络中有1个感染节点，其它参数为：N=1 000，m=10，γ=0.5。

先横向对比3个子图：当网络总连边数K增大，网络传播阈值qc越小，这与式(17)相符。再观察各个子图：随着模块化系数Q的增大，传播阈值qc减小，验证了理论结果。从单个子图来看，随着Q的增大，传播阈值变小。因为在传播初期，病毒首先在社团内扩散，Q越大，社团内连边密度相对越大，较小的感染率即可使病毒在社团内先爆发开来。图中所标箭头处为理论阈值，它们与仿真结果接近。

图6表示传播阈值qc与网络连边数K的关系曲线，为了更清楚显示二者关系，该图采用双对数坐标，参数为N=1 000，m=10，Q=0.5，γ=0.2。实线(MF)是传播阈值表达式(式(16))的图形化，圆圈(MC)表示蒙特卡罗仿真结果。理论值与仿真值的趋势基本一致，传播阈值qc与网络连边总数K反相关。

4结语

传染病动力学建模作为对病毒传播进行定量理论研究的一种重要方法，受到病毒传播研究学者的广泛应用。近年来，研究者们发现并持续关注许多真实网络具有社团结构这一特性。本文引入模块化系数Q，基于随机网构建社团结构网络模型，控制各个网络参数以使所建模型符合现实网络情况，并基于该网络建立SIS病毒传播模型，分析病毒传播动力学。该社团结构网络的度分布仍呈泊松分布，但模块化系数越大，峰形越宽且峰值越小。数学分析和仿真结果表明：传播阈值反比于网络连边总数；传播阈值与社团强度反相关，强社团结构网络对应的传播临界值越小；但当感染率远大于阈值时，模块化系数Q会影响传播速度和到达稳态所用时间，较大模块化系数网络对应的传播速度先快后慢，较小模块化系数网络的传播速度反之，而模块化系数对稳态传播规模影响不大。

参考文献:

[1]Pastor-Satorras R, Vespignani A. Epidemic dynamics and endemic states in complex networks[J]. Physical Review E, 2001, 63(6): 066117.

[2]李翔, 刘宗华, 汪秉宏. 网络传播动力学[J]. 复杂系统与复杂性科学, 2010, 7(2-3): 33-37.Li Xiang, Liu Zonghua, Wang Binghong. On spreading dynamics on networks[J]. Complex Systems and Complexity Science, 2010, 7(23): 33-37.

[3]张海峰, 王阳阳, 汪秉宏. 行为反应对复杂网络上传染病动力学的影响[J]. 复杂系统与复杂性科学, 2012, 9(3): 13-21.

Zhang Haifeng, Wang Yangyang, Wang Binghong. The impacts of behavioral responses on the spreading of infectious diseases on complex networks[J]. Complex Systems and Complexity Science, 2012, 9(3): 13-21.

[4]Borge-Holthoefer J, Meloni S, Gon?alves B, et al. Emergence of influential spreaders in modified rumor models[J]. Journal of Statistical Physics, 2013, 151: 383-393.

[5]肖人彬, 张耀峰. 网络群体事件信息传播的演化博弈分析[J]. 复杂系统与复杂性科学, 2012, 9(1): 1-7.

Xiao Renbin, Zhang Yaofeng. Evolutionary game analysis of information spread in network mass events[J]. Complex Systems and Complexity Science, 2012, 9(1): 1-7.

[6]Gong Y W, Song Y R, Jiang G P. Time-varying human mobility patterns with metapopulation epidemic dynamics[J]. Physica A, 2013, 392(19): 4242-4251.

[7]Gong Y W, Song Y R, Jiang G P. Global dynamics of a novel multi-group model for computer worms[J]. Chinese Physics B, 2013, 22(4): 040204.

[8]Girvan M, Newman M E J. Community structure in social and biological networks[J]. PNAS, 2002, 99(12): 7821-7826.

[9]Borgatti S P, Mehra A, Brass D J, et al. Network analysis in the social sciences[J]. Science, 2009, 323(5916): 892-895.

[10] Centola D. The spread of behavior in an online social network experiment[J]. Science, 2010, 329(5996): 1194-1197.

[11] Onnela J P, Arbesman S, González M C, et al. Geographic constraints on social network groups[J]. PLoS one, 2011, 6(4): e16939.

[12] Wu X Y, Liu Z H. How community structure influences epidemic spread in social networks[J].Physica A, 2008, 387: 623-630.

[13] Huang W, Li C G. Epidemic spreading in scale-free networks with community structure[J]. Journal of Statistical Mechanics: Theory and Experiment, 2007, 2007(01): P01014.

[14] Zhang J P, Jin Z. Epidemic spreading on complex networks with community structure [J]. Applied Mathematics and Computation, 2012, 219(6): 2829-2838.

[15] Zhang H L, Guan Z H, Li T, et al. A stochastic SIR epidemic on scale-free network with community structure[J]. Physica A, 2013, 392(4): 974-981.

[16] Shu P P, Tang M, Gong K, et al. Effects of weak ties on epidemic predictability on community networks[J]. Chaos, 2012, 22(4): 043124.

[17] Chu X W, Guan J H, Zhang Z Z, et al. Epidemic spreading in weighted scale-free networks with community structure[J]. Journal of Statistical Mechanics: Theory and Experiment, 2009, 2009(07): P07043.

[18] Min Y, Jin X G, Ge Y, et al. The role of community mixing styles in shaping epidemic behaviors in weighted networks[J]. PLoS one, 2013, 8(2): e57100.

[19] Chen J C, Zhang H L, Guan Z H, et al. Epidemic spreading on networks with overlapping community structure[J]. Physica A, 2012, 391(4): 1848-1854.

[20] Liu Z H, Hu B. Epidemic spreading in community networks[J]. Europhysics Letters, 2005, 72: 315-321.

[21] Shao F, Jiang G P. Traffic driven epidemic spreading in homogeneous networks with community structure[J]. Journal of Networks, 2012, 7(5): 850-855.

[22] Peng X L, Small M, Xu X J, et al. Temporal prediction of epidemic patterns in community networks[J]. New Journal of Physics, 2013, 15(11): 113033.

[23] Li K Z, Fu X C, Small M, et al. Estimating the epidemic threshold on networks by deterministic connections[J]. Chaos: an Interdisciplinary Journal of Nonlinear Science, 2014, 24(4): 043124.

[24] Colizza V, Vespignani A. Invasion threshold in heterogeneous metapopulation networks[J]. Physical Review Letters, 2007, 99(14): 148701.

[25] Son S W, Bizhani G, Christensen C, et al. Percolation theory on interdependent networks based on epidemic spreading[J]. Europhysics Letters, 2012, 97(1): 16006.

[26] Wang Y B, Xiao G X. Epidemics spreading in interconnected complex networks[J]. Physics Letters A, 2012, 376(42): 2689-2696.

[27] Newman M E J, Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69(2): 026113.

(责任编辑李进)

Modeling and Analysis of Epidemic Spreading on Community Structure Network

LI Chanchana, JIANG Guopingb

(a.School of Computer； b.School of Automation, Nanjing University of Posts and Telecommunications, Nanjing 210003, China)

Abstract：Considering many real networks have the community structure property, in this paper, by introducing modularity coefficient and under its control, we build a community network model based on random network, which is used to simulate the real social networks. Then we investigate the epidemic spreading behaviors by mean field theory and get the mathematical expression of epidemic threshold, we also verify it by Monte Carlo simulations. It is found that the existing of community structure can change the network degree distribution, namely, the stronger community structure networks have wider degree distribution. And the stronger the community structure is, the smaller the virus spread critical value will be. Moreover, when the infection rate far away from the epidemic threshold, the transmission sizes of networks with different community structure intensity almost the same, that is, the change of modularity coefficient barely affects the epidemic prevalence.

Key words：complex network; community structure; epidemic spread; mean field

文章编号：1672—3813(2016)02—0067—07;

DOI:10.13306/j.1672-3813.2016.02.008

收稿日期：2014-07-07；修回日期：2014-12-31

基金项目：国家自然科学基金(61374180，61373136，61304169)；教育部人文社科规划基金(12YJAZH120)；教育部高等学校博士点基金(20103223110003)；江苏省“六大人才高峰”项目(RLD201212)

作者简介：李婵婵(1989-)，女，山西运城人，博士研究生，主要研究方向为复杂网络与信息安全。 通讯作者：蒋国平(1966-)，男，江苏扬中人，博士，教授，主要研究方向为混沌系统与复杂网络。

中图分类号：N93；N94

文献标识码：A