基于动态参照点的多主体有限理性路径选择模型
李雪岩,李雪梅,李学伟,赵 云,邱荷婷
(北京交通大学经济管理学院 北京 100044)
基于动态参照点的多主体有限理性路径选择模型
李雪岩,李雪梅,李学伟,赵云,邱荷婷
(北京交通大学经济管理学院 北京 100044)
摘要:为了研究有限理性假设下出行者的自适应调整行为对交通网络分流的影响,利用累积前景理论结合演化元胞自动机建立了具有个体交互机制的多主体路径选择模型。在模型中将出行者划分为风险追求者与风险厌恶者,基于出行时间可靠性并借鉴元胞遗传算法的思想设计了具有异质特点的出行者动态参照点及其演化规则,使出行者个体能够依据决策环境的变化动态地调整自身的出行时间预算,更加符合出行者的实际行为特征。最后将多主体参照点演化规则与传统的相继平均算法相结合,求解路网配流。研究发现:演化模型较好地继承了传统模型中的路径分流特点;不同的出行者类型比例及出行者的信息接收程度是影响路网分流结构的重要因素。
关键词:有限理性;多主体;风险;元胞遗传算法;动态参照点;交通流量分配;
0引言
不确定的交通需求、出行者的动态选择行为决定了交通系统具有动态性、时变性、随机性等特征,也意味着交通系统是一个典型的复杂系统。传统的动态交通分配模型往往基于期望效用理论(expected utility theory,EUT)或随机效用理论(random utility theory,RUT)来研究出行者的路径选择行为和路网分流均衡问题,在该研究框架下,通常假设出行者具备完美信息及完全理性,按照效用最大或阻抗最小原则进行路径选择。然而,无论是在交通网络中还是在其他领域,许多实际现象和实验数据都与这种完全理性的假设不符[1—3]并且无法用上述两种理论解释。
通过心理学实验,Kahneman和Tversky发现人们对效用进行判断时往往会设定一个十分重要的基准,即“参照点”,然后依据实际效用与参照点的相对位置进行决策,参照点的选取对决策结果会产生至关重要的影响,根据这一思想,先后提出了前景理论(Prospect Theory)[4]与累积前景理论(Cumulative Prospect Theory)[5],这两大理论被不少学者应用于出行行为研究中。Erel Avineri[3]采用基于固定参照点的累积前景理论建立了一个具有反馈学习机制的出行选择模型,研究了出行时间可靠性与出行者时间敏感度之间的关系;Jou Rong Chang[6]通过对参照点及风险态度等相关参数进行基于实证数据的估计,建立了基于累积前景理论的高速公路司机驾驶选择模型,研究发现累积前景理论较好地反映了实际当中的驾驶选择行为;Xu Hongli[7]将出行时间预算设置为参照点,基于累积前景理论建立了一个路径选择模型,进一步,在时间预算的基础上,通过设置不同出行者的理想准点到达概率从而构造了不同类别的参照点[8];Paolo Delle Site[9]建立了一个基于“参照点依赖”的随机用户均衡模型,以路径流量和时间作为参照点变化依据,研究了出行者的实际选择与其参照路径的偏差现象;王伟[10]在基于累积前景理论的随机网络均衡模型中将期望-超额出行时间作为内生参照点,模拟了出行者同时参考出行时间的可靠性和不可靠性时路网的分流情况;Giselle de Moraes Ramos[11]在利用前景理论研究出行行为时设计了出行者同质及异质条件下的参照点及其依据出行经验对参照点的更新机制;张波[12]以早高峰工作出行为研究对象,分析和设计了出行者同时选择出行路径和出发时间时的参照点设定规则。
通过上述文献可知,不同的参照点选取规则,会产生不同的交通网络分流结果。从不同文献中对于参照点的定义和描述来看,参照点的形成是一个复杂的心理过程,不同的决策者面对相同的决策环境可能会产生不同的参照点,而相同的决策者面对重复的决策环境也可能会产生不同的参照点。
一般认为,参照点具有“内生性”,来源于决策者的个性、历史经验、习惯等因素,但从实际当中人们的决策行为来看,这种“内生性”又不可避免地受到外部决策环境及各种信息传播的影响,常见的例子如人们对某个决策的风险态度经常会随着一些外部事件的发生而变化。目前,对参照点形成外部影响机制的研究并不多见。此外,在实际的出行决策中,受到出行信息、个人禀赋、决策环境等影响,出行者个体之间势必存在着理性程度的差异[13],虽然许多既有的研究已对出行者群体做出有限理性假设,但这种有限理性假设大多是以“同质”性为前提,较少涉及个体理性程度的差异问题。
就出行信息的影响而言,在实际的出行决策中,出行信息(如预计时间、路径状况等)在出行者群体中的交互、传播和学习[14]是影响出行者个体路径选择行为的重要因素,体现了出行者个体的自适应调整机制[15],依据复杂性科学的思想,这种具有交互性的自适应调整机制是交通系统内部产生正反馈的重要因素[16],而系统内部正反馈的产生势必会打破既有解析范式下的路网分流均衡。目前的研究大多将出行者的行为模式解析化,将整体行为简化为个体行为之和,认为局部个体间的异质特点可以相互抵消,忽略了局部反馈对整体均衡的扰动作用。
交通系统路径选择均衡的形成,应当是一个多主体参与的、具有局部信息交互作用及出行者自适应调整机制的动态演化过程。
针对上述问题,本文从实际决策中出行者的个体行为出发,在两个方面对既有的基于有限理性的路径选择模型做出了改进工作:1)利用元胞自动机对既有研究中解析范式下的选择模型进行离散化,将每一个元胞抽象为一个出行者,通过出行风险态度及出行预算时间这两个属性刻画不同类型出行者的异质特点,从而形成多主体决策模型;2)借鉴元胞遗传算法中种群进化的思想建立出行者的信息交互机制及参照点的动态演化规则,本文提出的模型及算法可以为交通规划、人性化管理、动态诱导等交通管理方案的实施提供一定参考。
1基本假设
1.1路网假设
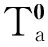
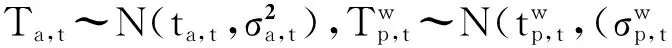
根据流量守恒原理,存在如下等价关系:
(1)
(2)
(3)
(4)
1.2出行者假设
与既有研究不同,本文不再将出行者视为一个具有同质特点的群体,而是依据多主体思想及自底向上的建模思想,将出行者还原为一个个具有自适应调整能力的个体来研究其路径选择行为,故本文对出行者做出如下假设:
1) 不同的出行者为出行活动预留的时间不同,该指标的变化取决于出行者的风险态度及出行信息交互情况。
2) 出行者个体依据风险态度分为两种类型:风险追求型与风险厌恶型,风险追求型的出行者对未来的路况较为乐观,倾向于在未来的出行活动中预留更少的出行时间;而风险厌恶型的出行者则比较保守,倾向于在未来的出行活动中预留更多的出行时间。
3) 出行者个体具有出行信息的学习能力,并且其对路径特点的判断会受到周围信息的影响。每次出行活动完成后,不同出行者个体之间会进行信息交互,从而更新自身的出行偏好,如出行活动预留的时间、路径选择概率。
2模型建立
2.1多主体路径选择元胞自动机模型
作为探索复杂系统的有力工具,元胞自动机已被证明能够较好地模拟交通系统中的路径选择[14]、交通运输服务选择[17]等行为,因此,依据上文假设,鉴于出行者的异质及信息交互特点,本文采用元胞自动机来建立出行选择决策模型。
1) 元胞空间:n×n的网格,显然,dw=n2。
2) 邻居形式:Moore型邻居,即每个出行者拥有8个邻居,如图1所示:
3) 元胞状态:用一个四元组表示
(5)

4)演化规则:每完成一次OD对间的出行活动后,出行者都会依据风险态度及信息交互机制更新自身的出行预留时间,本文引入元胞遗传算法的思想来模拟这一过程,具体步骤见2.3节。
2.2基于累积前景理论的多主体路径选择过程
2.2.1参照点
在前景理论的假设中,人们往往依据效用的相对数值而非绝对数值来衡量一项决策的优劣,因此,“参照点”的设置尤为重要,一般而言,出行者为了避免迟到,均会在出发前对路上所消耗的时间做一个预计,基于此,Lo H K[18]提出了出行时间预算的概念,进一步,Xu Hongli[7—8]及王伟[10]将这一概念应用于出行时间参照点的确定。本文继续借鉴这一方法,构建多主体的出行时间参照点。
(6)
(7)
(8)
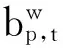
2.2.2路径选择决策
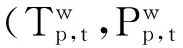
累积前景理论的基本观点之一就是在不确定的条件下,人们习惯将决策结果相对于参照点的相对值作为衡量决策效用的标准,依据这个相对值将每种可能的决策结果评判为“收益”或“损失”,具体可用价值函数表示为
(9)
其中,0<α,β<1,α与β反映了出行者的风险偏好水平,其值越大表示出行者对风险越敏感,反之对风险越不敏感;λ表示损失规避系数,其值越大,表示出行者对损失的规避程度越高。
决策权重函数表示为
(10)
则累积决策权重表示为
(11)
(12)
如t时刻路网达到均衡状态,则出行者个体(i,j)选择OD对间路径p的理想概率为
(13)
2.3基于元胞遗传算法思想的多主体出行信息交互过程
2.3.1基于元胞遗传算法的多主体建模思想
元胞遗传算法是元胞自动机与遗传算法的有机结合[20],其原理在于通过元胞空间内个体元胞之间的信息交互,使种群内的优秀信息得到传播和保存,本文则将元胞遗传算法的思想和演化规则引入多主体路径选择模型中的信息交互过程。
由前文的出行者假设可知,每完成一次出行活动后,不同出行者之间都会通过信息交互来更新下一次出行的预算时间(参照点),这种个体出行预算时间的更新方式可借助元胞遗传算法的演化规则表示如下。
2.3.2参照点演化规则
对于t时刻的出行活动,个体(i,j)的参照点按照如下步骤演化。
步骤2:选择。个体(i,j)与“邻居”进行信息交流,选择周围“邻居”中OD对间平均出行时间预算最长与最短的个体:
(14)
(15)
步骤3:交叉。个体(i,j)依据自身的风险态度类型更新其时间预算系数ρt(i,j),
如果个体(i,j)为风险追求型,即l(i,j)=1,则时间预算系数更新如:
ρt+1(i,j)=(1-pc)·ρt(i,j)+pc·ρt(imin,jmin)
(16)
如果个体(i,j)为风险厌恶型,即l(i,j)=0,则时间预算系数更新如下:
ρt+1(i,j)=(1-pc)·ρt(i,j)+pc·ρt(imax,jmax)
(17)
其中,参数pc表示出行者以何种程度吸收周围的出行信息,该参数决定了出行者参照点的位置变化。
通过上述步骤,出行者完成参照点的更新。可见,在一定的信息传播范围内(邻居),风险追求型的出行者越来越倾向于预留较少的出行时间;而风险厌恶型的出行者越来越倾向于预留较多的出行时间。元胞遗传算法规则的引入,恰当地刻画了这一过程。
2.4路网均衡模型
依据随机用户均衡原理,多主体路网平衡状态满足条件:
(18)
3模型求解演化算法
本文将MSA(Method of Successive Average)算法与多主体参照点演化规则进行有机结合,形成多主体有限理性(Bounded Rational Multi-Agent)路径选择演化算法(BRMA-MSA),具体步骤为
步骤1:路径搜索。将OD对之间的所有简单无环路径作为有效路径集Rw。
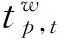
步骤4:依据2.3.2节的参照点演化规则更新出行者的风险态度系数ρt(i,j)。

(19)

步骤6:令t=t+1,返回步骤3。
4算例分析
4.1算例网络
以目前文献中广泛采用的如图3所示的路网为例,对本文提出的模型进行模拟。对于路径行程时间,则采用BPR函数:
(20)
4.2参数取值
此外,依据Kahneman,Tversky及Prelec所给出的参数取值[19],本文取α=β=0.88,λ=2.25,γ=0.74;其余参数设置为:θ=1,dw=n2=2 500。
4.3路径选择演化结果
令pr=0.5,pc=0.5,对本文模型进行仿真,演化50步后,出行者群体的路径选择趋于稳定,将演化过程中的路径属性统计如表2:
由表2可见,路径3与路径5的流量相对较大,这是由于路径3与路径5的行程时间及其方差均相对较小,继而路径前景相对较大;虽然路径6也具有较小的行程时间方差,但由于其行程时间最大,路径前景最小,故其流量最小。演化结果说明,本文提出的模型较好地继承了基于累积前景理论的路网分流模型的特点,体现了出行者群体的有限理性。
4.4出行者类型及信息接收程度变化仿真
4.4.1路径前景
调整出行者中不同风险态度人群的比例pr及出行者的信息接受程度pc,演化至稳定状态,图4给出了演化过程中元胞空间内不同路径的前景值随pr及pc的变化情况:
观察图4不难发现:1)在出行者群体不同的风险态度比例条件下,路径前景均呈现了随出行者信息接受程度pc的变化趋势,表明路径分流具有显著的参照点依赖效应。2)当出行者中风险追求者的比例较小时(pr=0,pr=0.3),各条路径的前景效用值随出行者信息接收程度的增加呈现增长趋势,且pr越小,增长幅度越大;而当出行者中风险追求者的比例较大时(pr=0.6,pr=0.9),各条路径的前景效用值随出行者信息接收程度的增加呈现降低趋势,且pr越大,降低幅度越大。这是由于,当风险追求者的比例较小时,出行者总体更加倾向于预留较长的出行时间,其出行前景表现为“收益”的概率较大,在此基础上,出行者的信息接收程度越大,则意味着出行者“风险规避”的信念越强烈,使其不断预留更长的出行时间,则不同路径前景值的增长幅度就越大;当风险追求者的比例较大时,出行者总体更加倾向于预留较短的出行时间,其出行前景表现为“损失”的概率较大,在此基础上,出行者的信息接收程度越大,则意味着出行者“风险追求”的信念越强烈,使其不断预留更短的出行时间,则不同路径前景值的降低幅度就越大。
进一步,表3给出了不同路径之间前景值的差异随出行者信息接收程度的变化情况,由累积前景理论可知,路径之间前景效用的差异是决定出行者群体在路网中分流的重要因素,结合表3可以发现,在出行者信息接收程度的变化过程中,风险追求者比例pr越小,不同路径前景之间的差异变化越大,即此时出行者信息接收程度(交互作用)的大小会较大程度影响其对不同路径优劣的判断,而当pr增大时,不同路径前景之间的差异变化减弱,即此时出行者信息接收程度(交互作用)的大小对不同路径优劣的判断影响较小。这种不同路径之间前景值差异的变化,体现了多主体在不同风险态度及信息接收程度影响下的有限理性特点。
4.4.2路径分流
调整出行者中不同风险态度人群的比例pr及出行者的信息接收程度pc,演化至稳定状态,图5给出了演化过程中不同路径的流量随pr及pc的变化情况。
通过图5可见,在演化中调节出行者群体中不同风险态度人数的比例pr,形成了不同的路网分流结构,当pr由小变大(即风险追求者由少变多)时,路径1,5的流量增加,路径2,3,4,6的流量减小,由4.4.1节可知,这是由于当出行者具有不同的风险态度时,不同路径的前景效用值发生了变化。此外,当pr较小(即风险厌恶者较多)时,出行者的信息接收程度(交互作用)对路径流量的影响较大;当pr较大(即风险追求者较多)时,出行者的信息接收程度(交互作用)对路径流量的影响较小;由表3可知,这是由于在不同信息接收程度下,对于出行者而言,不同路径之间前景效用的差异发生了变化。
结合4.4.1节与本节的仿真结果可知,路网分流结构的差异是多主体有限理性条件下出行者信息接收程度与群体风险态度共同作用的结果。
5实际采集数据分析
为进一步说明本文所建立模型的实际意义,特选取北京市海淀区交大东路与高粱桥斜街作为交通流量实际采集对象,记录驶向西直门方向的车流量。选取原因在于:两条路径的交汇点即位于西直门商业枢纽与换乘枢纽,是大量车流流向的目的地,两条路径的流量分配情况能更好体现出行者群体的路径选择行为。
表4给出了北京市海淀区“交大东路”与“高粱桥斜街”的交通流量数据采集结果,不难发现:
1)两条路径在高峰期与非高峰期的车流量具有明显差异,这是由于,出行者群体在高峰期与非高峰期往往具有不同的出行时间参照点(风险态度),高峰期的出行者往往风险厌恶者占多数(预留较多出行时间),非高峰期的出行者往往风险追求者占多数(预留较少出行时间),可见,上述采集结果较好地体现了出行者群体风险态度对路径流量的影响。
2)高峰期选择两条路径的出行者人数比例差异大于非高峰期(在高峰期,驶向西直门方向且选择“交大东路”的出行者是选择“高粱桥斜街”的1.6倍,而非高峰期则是1.2倍)。这说明,高峰期(风险厌恶者占据多数)出行者群体的路径选择行为对路径流量的影响更大,而在本文的模型中,出行者群体路径选择行为通过多主体间的信息交互作用实现,因此,这一现象较好地印证了第4节中“当pr较小(即风险厌恶者较多)时,出行者的信息接收程度(交互作用)对路径流量的影响较大;当pr较大(即风险追求者较多)时,出行者的信息接收程度(交互作用)对路径流量的影响较小”这一仿真结果。
6小结
本文在前人工作的基础上,对路径选择模型中的出行者假设做出了进一步改进,基于自底向上的复杂系统多主体建模思想,刻画了出行者的风险态度差异及信息传播机制,设计了具有演化机制的动态参照点,从而使新模型进一步接近现实中人们的出行决策行为。通过路网分流算例仿真及相应的实证数据采集分析,发现出行者的异质特点(风险态度、信息接收程度)是影响其对出行前景效用感知及路网分流结果的重要因素,此外,本文提出的模型较好地解释了实际交通流分配中的流量变化现象。
本文只考虑了固定需求下的多主体路径选择情景,并且仅考虑了风险态度及信息接收程度的影响,因此,未来的研究包括:1)弹性需求下的多主体路径选择问题;2)将更多的多主体自适应属性引入路径选择模型。
参考文献:
[1]Simon H A.Behavioral model of rational choice[J].Quarterly Journal of Economics,1955,69:99-120.
[2]Ellsberg D.Risk,Ambiguity and the savage axioms[J].Quarterly Journal of Economics,1961,75(4):643-669.
[3]Avineri E,Prashker J N.Sensitivity to travel time variability:travelers learning perspective [J].Transportation Research Part C,2005,13(2):157-183.
[4]Kahneman D,Tversky A.Prospect theory:an analysis of decision under risk[J].Econometrica,1979,47(2):263-291.
[5]Tversky A,Kahneman D.Advances in prospect theory:Cumulative representation of uncertainty[J].Risk Uncertainty,1992,5(4):297-323.
[6]Jou R C,Chen K H.An application of cumulative prospect theory to freeway drivers'route choice behaviours [J].Transportation Research Part A,2013,49(3):123-131.
[7]Xu H L,Zhou J, Xu W.A decision-making rule for modeling travelers'route choice behavior based on cumulative prospect theory [J].Transportation Research Part C,2011,19(2):218-228.
[8]Xu H L,Zhou J,Xu W.A prospect-based user equilibrium model with endogenous reference points and its application in congestion pricing [J].Transportation Research Part B,2011,45(2): 3111-328.
[9]Paolo De S,Francesco F.Stochastic user equilibrium with reference-dependent route choice and endogenous reference points [J].Procedia-Social and Behavioral Sciences,2012,54(10):547-556.
[10]王伟,孙会君.基于内生参考点的交通网络均衡模型[J].应用数学和力学,2013,34(2):190-198.
Wang Wei,Sun Huijun.Traffic network equilibrium model based on endogenous reference point [J].Applied Mathematics and Mechanics,2013,34(2):190-198.
[11]Giselle de M R,Winnie D,Serge H.Modelling travellers'heterogeneous route choice behaviour as prospect maximizers [J].The Journal of Choice Modelling,2013,6(3):17-33.
[12]张波,隽志才,林徐勋.基于累积前景理论的出发时间选择SDUO模型[J].管理工程学报,2013,27(1):68-76.
Zhang Bo,Juan Zhicai,Lin Xuxun.Stochastic dynamic user optimum model with departure time choice based on cumulative prospect theory [J].Journal of Industrial Engineering/Engineering Management,2013,27(1):68-76.
[13]Caspar G C,Harry J P. Measuring user benefits of changes in the transport system when traveler awareness is limited [J].Transportation Research Part A,2009,43(6):536-547.
[14]Ann van A,Erik R L.Self-organising behaviour in the presence of negative externalities:a conceptual model of commuter choice [J].European Journal of Operational Research,2004,157:501-513.
[15]度巍,黄崇超,肖海燕,等.信息系统下弹性需求随机用户均衡演化模型[J].交通运输系统工程与信息,2013,13(6):120-126.
Du Wei,Huang Chongchao,Xiao Haiyan,et al.Stochastic user equilibrium evolutionary model with elastic demand and advanced traveler information systems [J].Journal of Transportation Systems Engineering and Information Technology,2013,13(6):120-126.
[16]John H M, Scott E P. Complex Adaptive Systems: an Introduction to Computational Models of Social Life [M]. Princeton, New Jersey: Princeton University Press, 2007.
[17]寇勇刚,吴桐水,朱金福.航空服务创新的元胞自动机竞争演化模拟[J].系统工程理论与实践,2011, 31(6):1071-1076.
Kou Yonggang,Wu Tongshui,Zhu Jinfu.Simulating of evolution for the aviation service innovation competition with cellular automata [J].Systems Engineering Theory & Practice,2011, 31(6):1071-1076.
[18]Lo H K,Luo X W,Siu B W Y.Degradable transport network:travel time budget of travelers with heterogeneous risk aversion [J].Transportation Research Part B,2006,40(9):792-806.
[19]张波.基于前景理论的动态路径选择行为研究[D].上海:上海交通大学安泰经济与管理学院,2012.
Zhang Bo.Research on dynamic route choice behavior based on prospect theory [D].Shanghai:Antai College of Economics & Management Shanghai Jiao Tong University,2012.
[20]Asmaa A N,Ahmet T E, Tughrul A.Dynamic fault-tolerant three-dimensional cellular genetic algorithms[J]. J. Parallel Distrib.Comput,2013,(73):122-136.
(责任编辑耿金花)
Dynamic Reference Points based Bounded Rational Multi-Agent Model of Route Choice
LI Xueyan, LI Xuemei, LI Xuewei, ZHAO yun, QIU Heting
(School of Economics and Management, Beijing Jiaotong University, Beijing 100044, China)
Abstract:For the research of the impacts of travellers’ adaptive behavior on traffic flow assignment under bounded rationality, the multi-agent model of route choice with interaction among travellers is established using cumulative prospect theory and cellular automaton, in which travellers are grouped into two types: risk lovers and risk averse. Travellers’ heterogeneous dynamic reference points and evolution rules are designed based on travel time reliability and the idea of cellular genetic algorithm, so travellers can dynamically adjust their budget of travel time according to environment. The new model is more in tune with travellers’ actual behavior. Then by combining multi-passengers’ evolution rule with method of successive average, the new traffic flow assignment is solved. The study found that (1) the new model inherited the characteristics of the traditional traffic flow assignment model; (2) proportions of travellers with different risk attitude and travellers’ information receiving degree are critical factors which affecting traffic flow assignment.
Key words:bounded rationality; multi-agent; risk; cellular genetic algorithm; dynamic reference points; traffic flow assignment;
文章编号:1672—3813(2016)02—0027—09;
DOI:10.13306/j.1672-3813.2016.02.004
收稿日期:2014-05-23;修回日期:2014-12-10
基金项目:国家自然科学基金(71273023);高等学校博士学科点专项科研基金:(20130009110020);中央高校基本科研业务费专项资金(2013YJS039;2014YJS059)
作者简介:李雪岩(1987-),男,内蒙古呼和浩特人,博士研究生,主要研究方向为管理科学及复杂系统决策理论。
中图分类号:N945
文献标识码:A

