基于超网络的互联网金融均衡问题研究

张　婷， 米传民

(南京航空航天大学 经济与管理学院，南京 211106)



基于超网络的互联网金融均衡问题研究

张婷， 米传民

(南京航空航天大学 经济与管理学院，南京 211106)

摘要：为了研究互联网金融环境下日益复杂的金融网络，引入超网络理论，分析各决策者之间的竞争合作关系以及各自行为和最优化条件；考虑互联网环境下加剧的信用风险和操作风险，引入信用风险函数和操作风险函数，建立了由资金拥有者、互联网金融中介、传统金融中介、资金需求者构成的超网络模型。运用变分不等式理论，研究互联网金融超网络均衡解的存在性条件和唯一性条件，给出整个互联网金融网络的均衡条件，为下一步研究互联网金融发展趋势和饱和状态奠定基础。最后运用算例进行仿真，验证了模型的有效性。

关键词：互联网金融；超网络；均衡；变分不等式

0引言

互联网给人们的生活学习等方方面面带来了巨大的改变，特别是3G甚至4G网络、移动支付、云计算、社交网络、个性化推荐等现代信息技术，对传统的金融模式带来了巨大的冲击。目前，国内外已有很多学者致力于互联网金融领域的研究。

在国内，互联网金融这一概念首先由谢平提出，他指出互联网金融是不同于商业银行间接融资和资本市场直接融资的“第三种”融资模式[1]。国内对互联网金融的研究主要在探索性的初步阶段。柯珂[2]将风险管理引入一个具有电子交易的金融网络。宗潇泳[3]从狭义和广义两个维度界定了互联网金融的概念，探讨了互联网金融的理论基础。温信祥[4]分析了法国互联网金融的发展以及对中国的启示。喻平[5]基于广义虚拟经济新视角研究中国互联网金融的发展状况，提出互联网金融发展策略。国内对互联网金融的研究，大多数是从概念特征、商业模式、对传统银行影响、政府监管等角度进行的。互联网金融和传统金融的联系与区别、依存和排斥关系、共存和均衡状态，是整个金融行业发展过程中至关重要的问题，是目前研究的薄弱环节。

IliasSantouridis[6]调查了希腊网上银行是否被接受的决定性因素，采用了访谈式调查问卷，发现有效性、可信度和舒适性决定了对该网上银行渠道的使用与否。Eunkyoung Lee[7]用实证研究了羊群行为在网络P2P贷款中的存在，发现在放牧行为上存在边际递减效应。Booth[8]将金融视为一个整体网络来进行分析。Anna[9—11]运用超网络理论研究金融中介网络的风险管理问题。Solorzano-Margain[12]利用网络理论来描述金融危机的蔓延。但针对互联网金融特点，运用超网络等分析工具进行互联网金融定量研究，尚处于空白。

本文认为，互联网金融是互联网与金融结合的一个新兴领域，为资金融通开辟了新的途径。在安全便捷的网络支付、移动支付、云计算等技术支持的基础上，在大数据、社交网络环境的背景下，互联网金融为资金供需双方提供了融资平台，降低了市场信息的不对称程度，提高了资金配置效率，降低了交易成本。从信息对称、风险、成本等方面，互联网金融中介同传统金融中介具有不同的特点，传统的金融超网络模型难以表征互联网金融下的金融复杂系统。本文运用超网络理论，从资金流动机理上定量研究资金拥有者、互联网金融中介、传统金融中介和资金需求者之间的内在关系，建立互联网金融超网络模型来描述他们之间的相互作用，将整个金融行业的协调问题抽象为由上述决策者组成的超网络均衡问题。通过建立一个由“资金拥有者、互联网金融中介、传统金融中介、资金需求者”构成的超网络模型，分析模型中各个决策者的净收入最大化和风险最小化目标，以及他们之间的竞争合作关系。利用变分不等式表述使该互联网金融超网络达到均衡状态的条件，并证明其存在性和唯一性。

1互联网金融超网络模型

本文针存在互联网金融的典型融资过程，构建一个包括H个资金拥有者、I个互联网金融中介、J个传统金融中介和K个资金需求者的融资网络，第I+1个节点表示资金拥有者不进行投资的情况。图1描述了互联网金融系统的网络图。

第1层表示资金拥有者，符号h表示一个特定的资金来源。第2层表示互联网金融中介，符号i表示一个特定的互联网金融中介商，第I+1个节点表示资金拥有者不进行投资的情况。第3层表示传统金融中介，符号j表示一个特定的传统金融中介商。底层表示资金需求市场，符号k表示一个特定的资金需求者。其中实线表示资金从资金拥有者通过互联网金融中介和传统金融中介到达资金需求者的过程(例如小额资金拥有者将资金存入余额宝，通过天弘基金到达资金需求市场)。虚线表示资金不通过互联网金融中介直接从资金拥有者到达传统金融中介的过程(例如商人直接将资金存入银行)，以及资金不通过传统金融中介直接从互联网金融中介到达资金需求者的过程(例如资金拥有者通过P2P小额网贷向资金需求者提供资金)。

模型中的各个符号含义如下：

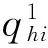
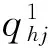
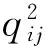
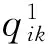
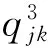
ρ：为相应的投资价格；

c：为相应的交易费用；

ci：互联网金融中介的转化费用；

cj：传统金融中介的转化费用；

Sh：资金拥有者h的资金拥有量；

rh：资金拥有者h对风险的承受能力；

ri：互联网金融中介i对风险的承受能力；

rj：传统金融中介j对风险的承受能力；

rk：资金需求者k对风险的承受能力。

符号中上角标为1表示此符号为第一层决策者的相关符号，上角标为2表示此符号为第二层决策者的相关符号，以此类推。

2互联网金融超网络中各层决策者的行为分析和最优化条件

在该网络中，资金拥有者、互联网金融中介、传统金融中介均为多目标决策者，假定这些决策者不仅追求净收入最大化，还追求风险最小化，引入一个可变权重的惩罚项来表示风险。在互联网环境下，金融行业所面临的风险越发扩大，主要是市场风险、信用风险和操作风险。市场风险作为系统风险，是整个金融网络中各个决策者都面临的风险，由风险价值惩罚函数来衡量。引入互联网金融后，降低了进行金融投资的门槛，向普惠金融更进一步，但同时也面临大量交易者带来的更广泛的信用风险。同时互联网金融中介商的加入也为整个金融中介行业带来了激烈的竞争，提出了更高的操作水平要求，要求中介商掌握更多的投资技巧和方法，获取更多的利益。在互联网环境下，对整个金融网络包括投资者、中介商等的电脑、网络的软硬件设备提出了更高的要求，操作风险中的技术风险部分也不断增大。本文创造性建立了信用风险函数和操作风险函数来分别表示互联网金融中介和传统金融中介所面临的信用风险和操作风险。区别于文献[11]，本文中的风险代表了不确定性，即可能带来损失、获利或者是无损失也无获利，风险与收益成正比。因此，在操作风险函数中，本文同时考虑了操作技巧带来的超额收益和技术风险带来的损失。

2.1资金拥有者的行为分析和最优化条件

对每一个资金拥有者而言，所投资的资金数目不能超过他所拥有的资金，小于等于表示了存在不投资的可能性。

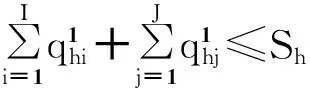
(1)

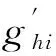
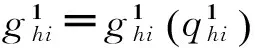
(2)

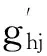
目标1净收入最大化

(3)

目标2风险最小化

(4)

考虑资金拥有者的风险态度将决定他可以承受的风险大小，加入可变权重来表示他对于风险的接受程度，得出风险惩罚价值函数

(5)

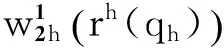
参照文献[6]和文献[12]中的证明，同理可证式(5)是严格凹函数，因此满足所有资金拥有者的均衡条件就可以表达为变分不等式[12-14]

(6)

2.2互联网金融中介的行为分析和最优化条件

对每一个互联网金融中介而言，所投资的资金数目不能超过他所拥有的资金。

(7)

(8)

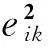
风险惩罚价值函数为

(9)

同理可证式(9)是严格凹函数，因此满足所有互联网金融中介的均衡条件就可以表达为变分不等式[12-14]

(10)

2.3传统金融中介的行为分析和最优化条件

对每一个传统金融中介而言，所投资的资金数目不能超过他所拥有的资金。

(11)

风险惩罚价值函数为

(12)

同理可证式(12)是严格凹函数，因此满足所有传统金融中介的均衡条件就可以表达为变分不等式[3-6, 12-14]

(13)

2.4资金需求者的行为分析和均衡条件

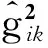
假设连续的需求函数dk是市场价格向量ρ4的函数，则

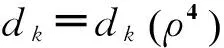
(14)

那么对所有的互联网金融中介

(15)

对所有的传统金融中介

(16)

除此之外，还有

(17)

约束条件式(15)表示资金需求者k会从互联网金融中介i处购买金融产品，如果互联网金融中介商的所有支出费用的总和不超过需求者愿意支付的价格。约束条件式(16)表示资金需求者k会从传统金融中介j处购买金融产品，如果传统金融中介商的所有支出费用的总和不超过需求者愿意支付的价格。约束条件式(17)表示如果资金需求者愿意支付给金融产品的价格是正的，则需求市场产品的数量是恰好等于需求的。

在均衡条件下，条件约束式(15)(16)(17)适用于所有需求市场，并且能表达成这样的变分不等式[3-6]

(18)

3均衡解的存在性条件和唯一性条件

均衡解的存在性条件：

假定存在正的常数M，N，R，使得

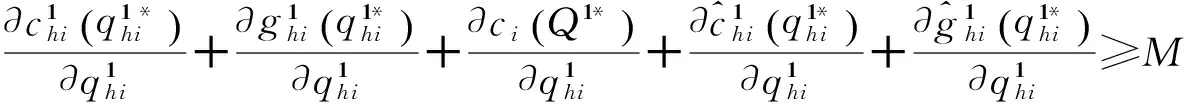
(19)

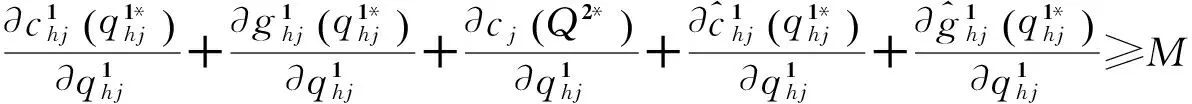
(20)

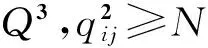
(21)

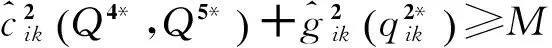
(22)

(23)

(24)

那么，变分不等式至少存在一个解。

均衡解的唯一性条件：假定式(6)(10)(13)(18)中的向量函数是(Q1，Q2，Q3，Q4，Q5，ρ4)关于是严格单调的，那么一定存在一个唯一的金融流(Q1*，Q2*，Q3*，Q4*，Q5*)和唯一的需求价格向量ρ4*，满足互联网金融网络的均衡条件。

4算例仿真

为验证上述构建的互联网金融超网络模型的科学有效性，参考文献[15]和[16]，建立一个由两个资金拥有者、两个互联网金融中介、两个传统金融中介和3个资金需求者组成的互联网金融超网络模型，结构图如图2。

对每一个资金拥有者和互联网金融中介以及传统金融中介j，设置

资金拥有者的资金拥有量

S1=32；S2=32

资金拥有者与互联网金融中介的交易费用函数

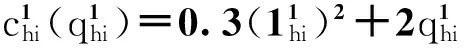
资金拥有者与传统金融中介的交易费用函数

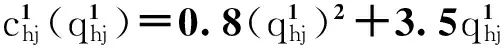
互联网金融中介与传统金融中介的交易费用函数

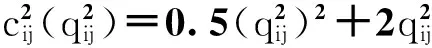
互联网金融中介与资金需求者的交易费用函数

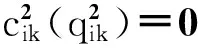
传统金融中介与资金需求者的交易费用函数

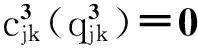
资金拥有者与互联网金融中介的信用风险函数

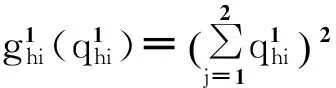
资金拥有者与传统金融中介的信用风险函数

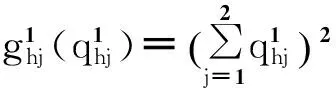
互联网金融中介与传统金融中介的信用风险函数

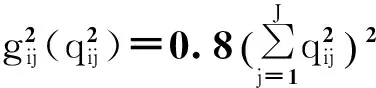
互联网金融中介与资金需求者的信用风险函数

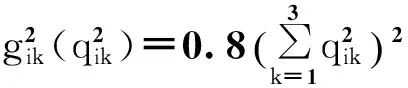
传统金融中介与资金需求者的信用风险函数

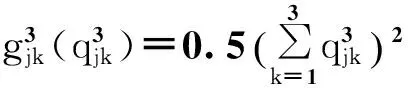
互联网金融中介的操作技巧系数和技术风险系数

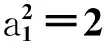
传统金融中介的操作技巧系数和技术风险系数

互联网金融中介与传统金融中介的操作风险函数

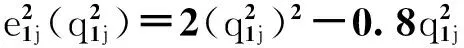
互联网金融中介与资金需求者的操作风险函数

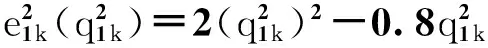
传统金融中介与资金需求者的操作风险函数

互联网金融中介和传统金融中介的转化费用函数

资金需求者的需求函数

参数设置为ε=10-4，α=0.02；Vi，Vj均为单位矩阵，其中的权重均设为1；其余的变量和函数都设为0。

将仿真算例中所设的函数具体表达式代入变分不等式中，使用Matlab2012b实现投影动态系统算法，经过3 174次迭代，收敛效果如图3所示，其良好的收敛效果验证了模型的有效性。

互联网金融超网络的最优均衡解为

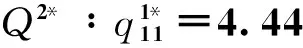
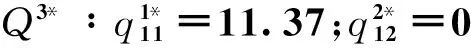
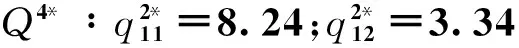
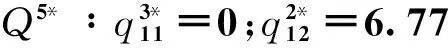
互联网金融中介的资金全部投资出去时的清仓价格为

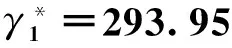
传统金融中介的资金全部投资出去时的清仓价格为

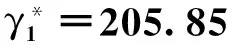
资金需求者的需求价格为

在这个例子中，

Q1*=45.84；Q2*=18.16；Q3*=21.83；Q4*=24.01；Q5*=39.99；

Q1*=45.84；Q3*+Q4*=45.84；Q1*=Q3*+Q4*

Q5*=39.99；Q2*+Q3*=39.99；Q5*=Q2*+Q3*

Q1*+Q2*=Q4*+Q5*=S1+S2=64

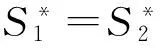
由Q1*=45.84；Q2Λ*=18.16可以看出，在互联网金融环境下，资金拥有者更多的投资于互联网金融中介而非传统金融中介，这对传统金融中介提出了更高的要求和挑战。事实上，互联网环境降低了金融中介的门槛，许多原来与金融并不相关的行业也在向互联网金融中介靠拢，例如余额宝的诞生。有识之士也纷纷选择互联网金融行业进行创业，例如有利网等。互联网金融中介正在蓬勃发展，更多的传统金融中介也积极向互联网金融中介转型。当然在互联网金融发展迅速的同时也需要政府和市场对其加强监管，保证整个行业的健康发展。整体上而言，互联网金融方便快捷，拥有大数据和云计算等先进技术的优势，能提高操作技巧，降低交易费用，更能满足资金拥有者的需求，必将在监管中慢慢完善，不断壮大。

5结语

本文考虑目前快速发展并对未来金融带来深刻影响的互联网金融问题，运用超网络理论，建立了一个由“资金拥有者、互联网金融中介、传统金融中介、资金需求者”构成的超网络模型。引入信用风险函数和操作风险函数，描述各个决策者所面临的信用风险和操作风险，其中认为操作风险不仅会让投资者面临技术风险所带来的损失，也会因为操作技巧而带来超额收益。利用变分不等式表达使整个互联网金融超网络达到均衡状态的条件，并证明其存在性和唯一性。最后，设计算例进行仿真，验证模型的有效性。本文所构建模型是将互联网金融作为一个整体进行抽象。下一步，可针对具体互联网金融模式的特点，如P2P等具构建更细化的超网络模型，深入研究不同的融资模式以及金融产品的差异化属性对互联网金融超网络均衡状态的影响。

参考文献:

[1]谢平,邹传伟. 互联网金融模式研究[J]. 金融研究, 2012, (12): 11-22.

Xie Ping,ZouChuanwei.Research of Internet finance model[J].Journal of Financial Research, 2012, (12): 11-22.

[2]柯珂, 樊智, 佘震宇, 等. 超网络时代的电子金融和风险管理[J]. 上海理工大学学报, 2011, (3):258-263.

Ke Ke, Fan Zhi, Yu Zhenyu, et al. Electronic finance and risk management in the supernetwork age [J]. Journal of University of Shanghai for Science and Technology, 2011, (3):258-263.

[3]宗潇泳. 互联网金融相关理论问题探析[J]. 经营管理者, 2014, (5): 42.

ZongXiaoyong. Related theoretical analysis of internet finance [J]. Managers’ Journal, 2014, (5): 42.

[4]温信祥, 叶晓璐. 法国互联网金融及启示[J].中国金融, 2014, (2): 75-77.

Wen Xinxiang, Ye Xiaolu.French internet finance and enlightenment [J].China Finance, 2014, (2): 75-77.

[5]喻平, 蒋宝珠. 广义虚拟经济视角下的互联网金融发展研究[J]. 广义虚拟经济研究, 2014, (1): 60-68.

Yu Ping, Jiang Baozhu. The research on the development of internet finance based on the view of generalized virtual economy [J]. Research on the Generalized Virtual Economy, 2014, (1): 60-68.[6]Ilias S, Maria K. Investigating the determinants of internet banking adoption in greece[J].Procedia Economics and Finance, 2014, (9): 501-510.

[7]Eunkyoung L, Byungtae L. Herding behavior in online P2P lending: an empirical investigation[J]. Electronic Commerce Research and Applications, 2012, 5(11): 495-503.

[8]Booth G, Gurun U G, Zhang H. Financial networks and trading in bond markets [J]. Journal of Financial Markets, 2014, 18: 126-157.

[9]Nagurney A, Dong J. Supernetworks: Decision-Making in the Information Age [M]. Cheltenham:Edward Elgar Publishing, 2002.

[10]Nagurney A, Ke K. Financial networks with electronic transactions: modeling, analysis, and computations [J]. Quantitative Finance,2003, 3(2): 71-87.

[11] Nagurney A, Ke K. Financial networks with intermediation: risk management with variable weights [J]. European Journal of Operational Research, 2006, 172(1): 40-63.

[12] Solorzano-Margain J P, Martinez-Jaramillo S, Lopez-Gallo F. Financial contagion: extending the exposures network of the Mexican financial system [J]. Computational Management Science, 2013, 10: 125-155.

[13] 张哲. 基于变分不等式的金融超网络[D]. 大连: 大连海事大学, 2010.

Zhang Zhe. Research of financial supernetwork based on variationalinqualities [D]. Dalian: Dalian Maritime University, 2010.

[14] Dong J, Nagurney A. Bicriteria decision making and financial equilibrium: a variational inequality perspective [J]. Computational Economics, 2001, 17(1): 29-42.

[15] Nagurney A, Ke K. Financial networks with intermediation [J]. Quantitative Finance, 2001, 1(4): 441-451.

[16] Nagurney A, Cruz J. International financial networks with intermediation: modeling, analysis, and computations [J]. Computational Management Science, 2003, 1(1): 31-58.

(责任编辑耿金花)

Study on Internet Financial Equilibrium Problem Based on Supernetwork

ZHANG Ting, MI Chuanmin

(College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China)

Abstract:Under the development of the Internet finance, supernetwork theory was included to study the increasingly complex financial network. A framework was developed for modeling, analysis and solutions to multitiered Internet financial network problems with investors, Internet financial intermediaries, traditional intermediaries and investees. The competitive and cooperative relationships between various decision-makers were explicated, as well as their behavior and optimality conditions. Functions of credit risk and operational risk were included, considering the increasing credit risk and operational risk in the environment of Internet. Using the variational inequality theory, the existence and uniqueness of the equilibrium solution is studied.The governing equilibrium conditions of the Internet financial network is also given so that the trend and saturation condition of Internet finance can be studied later. Finally, a simulation example is given to verify the validity of the supernetwork model.

Key words:internet finance; supernetwork; equilibrium; variational inequality

文章编号：1672—3813(2016)02—0036—08;

DOI:10.13306/j.1672-3813.2016.02.005

收稿日期:2014-06-24;修回日期：2014-09-23

基金项目：Marie Curie International Incoming Fellowship within the 7th European Community Framework Programme(FP7-PIIF-GA-2013-629051)；中央高校基本科研业务费专项资金(NJ20140033，NR2015003)；江苏高校哲学社会科学研究项目(2015SJD039)

作者简介：张婷(1991-)，女，江苏昆山人，硕士研究生，主要研究方向为金融工程。

中图分类号：N94

文献标识码：A