不同营销模式中基于时间的影响传播方法研究*

刘　勇，曲思桐，王　楠，郭龙江

黑龙江大学计算机科学技术学院，哈尔滨150080

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(03)-0338-12



不同营销模式中基于时间的影响传播方法研究*

刘勇+，曲思桐，王楠，郭龙江

黑龙江大学计算机科学技术学院，哈尔滨150080

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(03)-0338-12

E-mail: fcst@vip.163.com

http://www.ceaj.org

Tel: +86-10-89056056

* The National Natural Science Foundation of China under Grant No. 81273649 (国家自然科学基金); the Natural Science Foundation of Heilongjiang Province under Grant No. F201430 (黑龙江省自然科学基金); the Scientific Research Fund of Heilongjiang Provincial Education Department under Grant No.12531476 (黑龙江省教育厅科学技术研究项目).

Received 2015-07,Accepted 2015-09.

CNKI网络优先出版: 2015-09-15, http://www.cnki.net/kcms/detail/11.5602.TP.20150915.1618.008.html

摘要：影响最大化问题是在社交网络上找到一组有影响力的用户，使得期望的影响范围最大化。然而，已有book=339,ebook=43的研究工作没有考虑用户之间有效的传播时间区间，而且忽略了营销时间对于选取初始用户的影响。基于真实用户动作日志，确定了用户之间有效的传播时间区间，并提出了一个基于时间的影响力分配模型（influence power allocating model based on time，IPAT）。根据该模型，提出了基于真实时间的影响力最大化问题（influence maximization problem based on time，IMPT）和饥饿营销模式中种集最小化问题（seed set minimization problem in hungry marketing，SMPHM），并证明了这两个问题都是NP-hard问题。为求解IMPT问题和SMPHM问题，分别提出了有效的近似算法A-IMPT（algorithm for IMPT）和A-SMPHM（algorithm for SMPHM），并证明了算法A-IMPT和A-SMPHM的近似比。多个真实社交网络数据集上的实验验证了算法AIMPT和A-SMPHM的有效性和高效率。

关键词：社会网；影响传播；传播时间区间；营销时间；饥饿营销

1　引言

随着社会的不断发展，近年来各类社交网站不断涌现出来，人们开始广泛使用诸如微博、facebook等社交网站。这些社交网之所以变得如此受欢迎，是因为它们使人与人之间的关系变得更加紧密。此外，大量社会网站的普及以及在其平台上提出的大量营销需求都彻底颠覆了传统的信息传播模式。商家通过社会网能将商品或创意在极短的时间内传播给尽可能多的用户。

社会网中一个引人关注的问题就是影响力最大化问题，这个问题会引起很多想要销售他们的产品、服务、创新想法的公司或个人的兴趣。它通过一个“word-of-mouth（口碑效应）”的方式来进行商品或创意的传播，而在线社会网络恰恰提供了很好的平台来处理这类问题。2001年，Domingos等人[1]将影响力最大化问题作为概率问题研究。2003年，Kempe等人[2]首次把这个问题形式化为一个离散优化问题：给定有向图G=(V，E)，正整数k，选择大小为k的初始种集S，在给定传播模型下，通过选取的种集S使尽可能多的节点受到影响。

影响力最大化问题已经被广泛研究[1-4]，但已有的研究往往忽略以下几点：（1）不考虑用户之间的有效传播时间区间；（2）忽略了真实的营销时间对选取初始用户的影响；（3）传统的影响力最大化问题并不适用于现实中的某些营销模式，更没有考虑营销时间在这些营销方式中的重要作用。

对于问题（1），通过对真实动作日志中大量的用户和动作的分析，发现用户和用户之间存在有效的传播时间区间。一个例子能帮助理解这一点。u和v是好朋友，由于工作较忙，u和v 3天以上才通一次电话，但每个周末u和v都一起吃饭，那么很明显，由于信息传播渠道的关系，u和v的传播时间一定大于3天，且一般来说会小于7天。真实的数据也证实了这一点。表1是在Last.fm数据集上提取的几个用户动作信息。其中A到B有边，C到D有边，表中时间均为以0时刻为基准的相对时间，如(A,a)=2表示在0时刻后2个时间间隔的2时刻，用户A执行了动作a。

经过分析，容易发现A传播到B的动作时间都在[5,12]这个区间内，也就是说营销时间小于5，传播发生的概率很小，可忽略不计；若在[5,12]的区间内，则根据营销时间动态调整传播概率；若给定营销时间超过12，则保持原有传播概率不变。本文通过真实动作日志确定了每条边上有效的传播时间区间，再根据具体营销时间动态进行影响力分配。

对于问题（2），同样在真实的数据集Last.fm上进行了实验，证实了本文的观点。表2是运用本文提出的基于时间的影响力最大化算法在不同营销时间限制下选择的种集。设种集个数k=3，表中T代表营销时间限制，例如10代表10个单位时间，S代表选择的初始种集（用节点ID号表示）。

Table 2　 Marketing time T and seed set inLast.fm dataset (k=3)表2　在Last.fm数据集上不同的营销时间与种集(k=3)

从表2中可以看出，在不同的营销时间限制下，相应选取的种集也不同。因此，根据不同的营销时间来确定影响力的分配并选取相应的种集是合理的。

针对问题（3），考虑一个真实生活中的营销场景:小米手机自从上市以来一直受到人们的追捧和关注。原因在于小米手机选择了一种不同的营销方式——饥饿营销。饥饿营销是近几年很有代表性的营销方式，即供应商在固定时间内有意调低供应量，以期制造供不应求“假象”来长期维持商品较高利润率的一种营销策略。而在饥饿营销的短期销售过程内，在商家规定了固定的销售时间和期望的影响范围（商品供应量）这个条件下，人们可以找出销售目标客户中的最少初始用户(最小的种集)来进行产品的初始传播。不仅满足了商家对短期销售时间的要求，又达到了长期节省成本的目的。针对以上情景，本文提出了一种传统影响力最大化问题的变体，即在饥饿营销中基于时间的种集最小化问题。

本文主要贡献如下:

（1）基于用户的动作日志，确定用户之间传播的有效时间区间，并提出了一个基于时间的影响力分配模型（influence power allocating model based on time，IPAT）。根据该模型提出了基于时间的影响最大化问题（influence maximization problem based on time，IMPT），证明了该问题是NP-hard问题，并提出了求解IMPT问题的高效近似算法A-IMPT（algorithm for IMPT）。

（2）首次提出饥饿营销中基于时间的种集最小化问题（seed set minimization problem in hungry marketing，SMPHM），证明了该问题为NP-hard问题，并提出了求解SMPHM问题的高效近似算法A-SMPHM （algorithm for SMPHM），同时证明了A-SMPHM的联机近似比。

（3）多个真实的社会网数据集上的实验结果表明，本文算法能有效并高效求解IMPT问题和SMPHM问题。

本文组织结构如下:第2章介绍了相关工作；第3章给出了影响力分配模型及问题定义；第4章详细阐述了A-IMPT和A-SMPHM算法；第5章给出了实验及分析；第6章总结全文。

2　相关工作

2001年，Domingos等人[1]首次提出了在社会网上寻找具有重要影响力的用户进行产品营销的问题。Kempe等人[2]在2003年第一次将影响力最大化的问题定义为离散优化问题。Kempe等人[3-4]证明了影响力最大化问题是NP-hard问题，并提出了具有1-1/e-ε近似比的贪心算法。虽然得到了较好的近似比，但由于使用了大量的蒙特卡洛模拟估计影响范围，并不适用于大型社会网络。2007年，Leskovec等人[5]提出CELF（cost-effective lazy forward）优化对贪心算法进行了改进，大大提高了贪心算法的效率。Chen等人[6]在2009年提出了一个Degreediscount启发式算法，运行速度非常快，获得了很高的扩展性。Chen等人[7]在2010年提出了基于IC模型的启发式算法PMIA（prevalent marketing influence allocation），利用路径估计影响传播。Goyal等人[8]在2010年提出了获取边上影响概率的方法。Jiang等人[9]在2011年提出了一个基于模拟退火（simulated annealing）的方法解决影响最大化问题。2013年Li等人[10]提出具有遵从感知的影响力最大化问题，考虑了个人接受别人对自己影响的能力。2014年Li等人[11]提出关于地理感知的影响力问题，加入了地理信息因素。Feng等人[12]在2014年提出具有时间衰减的影响力最大化问题，但是他单纯用一个衰减因子更新影响力，并没有考虑到真实数据。2014年Barbieri等人[13]提出基于主题的影响力最大化问题，将问题细化到不同的主题分布上。

然而，上述所有模型都是人为设置用户之间的传播概率，这显然是不合理的，在生活中用户之间的相互影响是受到很多因素限制的。2012年Goyal等人[14]提出基于数据的方法进行影响力最大化问题的计算，通过分析真实动作日志直接计算节点的影响力。但却没有考虑影响传播过程中时间因素对结果的影响。即用户之间的影响具有有效传播时间区间，营销时间不同，最终选取的种集也不一样。

而且，已有的研究一般只考虑解决传统的影响力最大化问题，并不针对其他的营销方式考虑相应的解决方案，近年来越来越多的营销方式的出现也证实了影响传播在这些真实情境中的具体应用价值，因此本文也首次提出了饥饿营销中基于时间的种集最小化问题。

3　传播模型及问题定义

本文给出两种获取有效传播时间区间的度量，提出了基于时间的影响力分配模型，并给出了基于时间的影响最大化问题和饥饿营销中基于时间的种集最小化问题的形式化定义。

3.1获取有效传播时间区间

给定有向图G=(V,E)，动作日志A，A中每条记录格式为(user,action,time)，例如(a,3,4)表示用户a在4时刻执行了动作3。本文利用动作日志和用户的关系计算用户之间的有效传播时间区间，提出两种获取有效传播时间区间的度量。

（1）最大最小值（maximumminimumvalue，MMV）

直观地获取两个用户历史传播时间间隔的最大和最小值作为有效传播时间区间，定义如下：

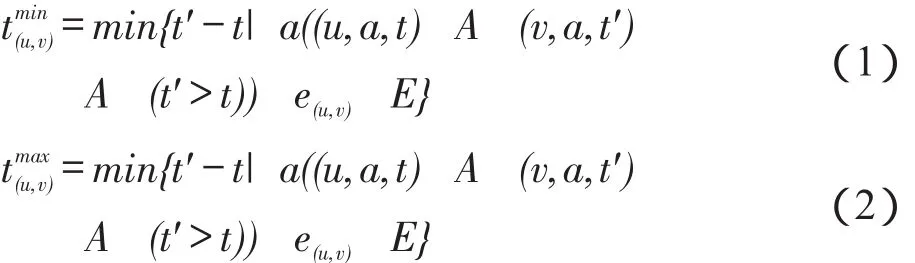
其中，eu,v∈E表示从节点u到节点v有边；区间作为u到v的有效传播时间区间。

（2）平均值+标准差（average value standard value，AVSV）

最大最小值法可能会受到特殊传播事件的干扰，因此提出平均值+标准差方法来更准确地表示有效传播时间区间，定义如下：

其中，μu,v和δu,v分别表示u到v传播时间间隔的均值和标准差，定义如下：最终

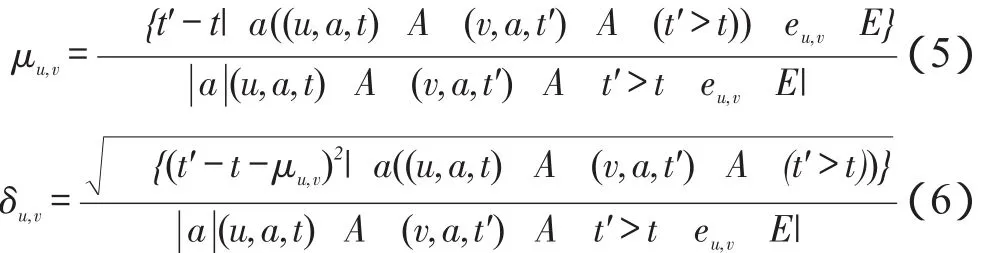
为u →v的有效传播时间区间。图1给出了一个具有有效传播时间的例子。

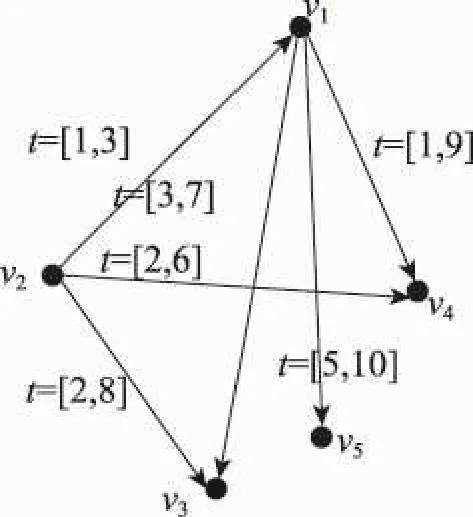
Fig.1　 Social network with effective propagationtime interval图1　带有有效传播时间区间的社会网

其中，tv1,v5=[5,10 ]表示节点v1到节点v5的有效传播时间区间是5时刻之后10时刻之前。也就是说，v1做出某个动作后，v5通常会在5时刻之后10时刻之前采取该动作。若给定营销时间少于5个单位时间，则传播几率很小，可忽略不计；若给定营销时间在[5,10]区间内，则应根据营销时间调整原有传播概率（见式（7））；若给定营销时间超过10单位时间，则应保持原有传播概率不变。

3.2影响力分配模型

在给出了用户之间的有效传播时间区间后，本文提出了一个基于时间的影响力分配模型IPAT。

给定有向图G=(V,E)，一个营销时间T，动作日志A。若营销时间T小于用户u→v之间的有效传播时间，那么u→v的传播几率很小，设定为u→v不传播。因此先将>T的所有边从图G中删掉，得到新的图G′=(V,E′)，图G′中都是在给定时间T内可能传播的边，接下来的操作在图G′上进行。

在T时间内如果图G′中存在边u→v，动作日志A中的某些动作将从节点u传播到节点v，此时v反过来为节点u分配影响力，同时v也对u的祖先节点迭代地分配影响力。在固定时间T内，定义直接影响v的节点集合为Nv={u|e′u,v∈E′}，那么节点v要对Nv中的∑每一个节点u分配影响力，定义为Ind，并且满足u∈NvInd≤1。对于Ind的值有很多种分配方法，本文根据营销时间T动态分配影响概率值，定义如下：

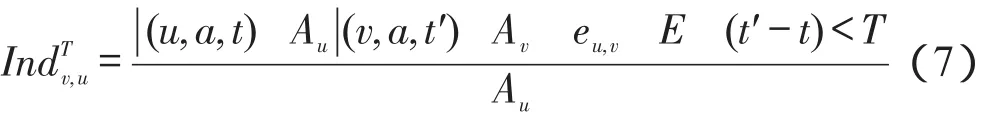
其中，Au是u执行的动作数；分子表示在T时间内u传播到v的动作个数。为保证，还需要对进行规范化，定义如下：

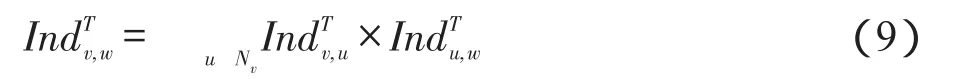
分配直接影响力后，开始由节点v迭代地向u的祖先w分配间接影响力，从而更新节点的影响力。v对祖先w分配的间接影响力Ind定义如下：其中，Indu,u=1。最后，对于每个节点u，把T时间内其他节点为u分配的影响力进行聚集，记为Inf，即为u在T时间∑内的影响力。

类似的，对于种集S⊆V，也可以根据营销时间T定义节点v对∑种集S分配的影响力，定义如下：

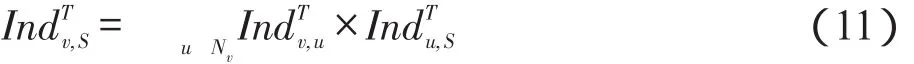
接下来利用图1的例子来说明IPAT模型。已知有向图G=(V,E)如图1所示，动作日志A={(v2,a,0),(v1, a,1),(v3,a,2),(v4,a,2),(v5,a,6),(v2,b,2),(v1,b,3)}。设T=4，根据IPAT模型，由于=5>T，删除v1→v5的边。接下来按照IPAT模型举例计算v4的影响力分配过程。首先，找到v4的直接邻居集合{v1,v2}，即Nv4 ={v1,v2}。根据动作日志发现节点v1共执行过a和b两个动作，而由v1传播到v4的动作只有a一个。根据式（7）可得Ind=1/2，Ind=1/2。分配直接影响力后，v4接着向自己的祖先节点分配间接影响力。因为v4向v2分配了直接影响力，v2向v1直接分配了影响力，所以v1是v4的祖先节点，v4应向v1分配一次间接影响力。根据式（9）来更新v4对v1的影响力，即Ind=1/2+1/2×1/2=3/4，其他节点同理。

3.3问题定义

基于时间的影响最大化问题(IMPT)：给定有向图G=(V,E)，动作日志A(user,action,time)，正整数k，固定的营销时间T，在IPAT传播模型下，计算影响范围最大的种集S(|S | =k)。

饥饿营销中基于时间的种集最小化问题(SMPHM)：给定有向图G=(V,E)，动作日志A(user, action,time)，固定的营销时间T，期望的影响范围Q，在IPAT传播模型下，计算能达到期望影响范围Q的最小种集S。

定理1基于真实时间的影响最大化问题是NP-hard问题。

证明设时间T为社会网中所有用户之间边上有效传播时间区间中的最大时间，即T=max{t|eu,v∈E}，那么IPAT模型也就等价于Goyal提出的CD （credite distribution）影响力传播模型[11]。因此，CD传播模型下的影响力最大化问题是基于时间的影响最大化问题的特殊情况。CD传播模型下的影响力最大化问题已经被证明是NP-hard问题，因此IMPT问题也是NP-hard问题。

定理2饥饿营销中基于时间的种集最小化问题是NP-hard问题。

证明如果SMPHM不是NP- hard问题，则SMPHM存在多项式时间算法A，使用算法A容易构造求解IMPT问题的多项式时间算法。过程如下：给定IMPT问题的一个实例(G(V,E) ,A,k,T)。设期望影响范围Q的取值从最大变化到最小(即Q∈{|V | ,|V | -1, |V| -2,…,1})，则可构造一系列SMPHM的实例(G(V,E) ,A,T,Q)。对SMPHM每个实例(G(V,E) ,A,Q)运行算法A，如果SMPHM的某个实例输出种集S大小为k，则显然S为IMPT问题实例(G(V,E) ,A,k,T)的最优解。上述过程最多调用|V|次算法A，显然整个求解过程仍是多项式时间。

根据定理1，IMPT问题是NP-hard问题，不存在多项时间算法。因此，SMPHM不存在多项式时间算法A，SMPHM问题是NP-hard问题。

4　基于真实时间的A-IMPT和A-SMPHM算法

本文给出求解基于时间的影响最大化问题的算法A-IMPT以及饥饿营销中基于时间的种集最小化问题的算法A-SMPHM。

首先输入真实的营销时间T，单位时间可以是小时、天、周等，可以依据具体的应用来确定。A-IMPT算法主要分3个阶段。第一阶段（第1~5行）对图G进行预处理，根据T来对图G=(V,E)进行删减得到图G′=(V,E′)。第二阶段（第6行）建立入度链表Inde_list，根据IPAT模型和营销时间T为节点分配影响力。同时计算节点的初始影响增益存入优先级队列queue。第三阶段（第7~10行）采用CELF优化方法贪心选取种集。每当选取一个种子节点后，迭代更新其他节点的影响增益。A-IMPT算法的伪代码如下所示。

算法1 A-IMPT算法

输入:社会网G=(V,E)，历史动作日志A，营销时间T，正整数k。

输出:T时间内具有最大影响范围的种集S(|S | =k)。

1. For each (u,v)∈E

4.删除边(u,v);

5.最后得到的图记为G′=(V,E′) ;

6. (Inde_list ,queue)= parentslink(G′,A);

7. S←∅;

8. While (|S|< k )

9. S=S⋃CELF(G′,Inde_list, queue, S);

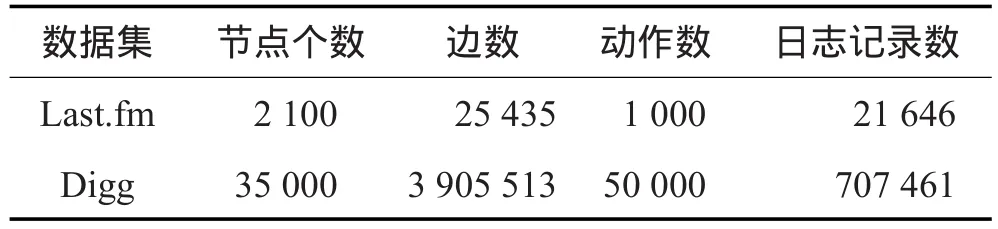
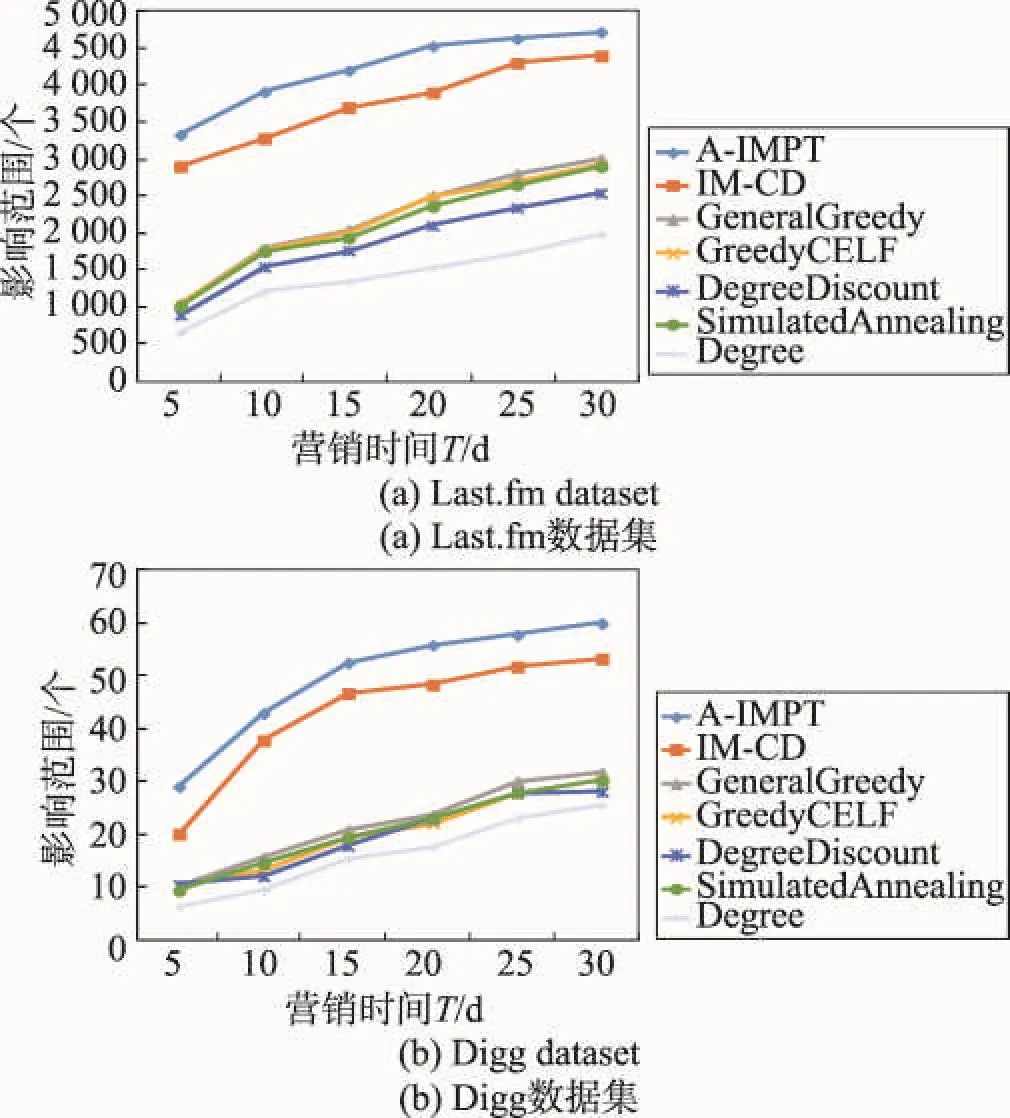
10. Return S;

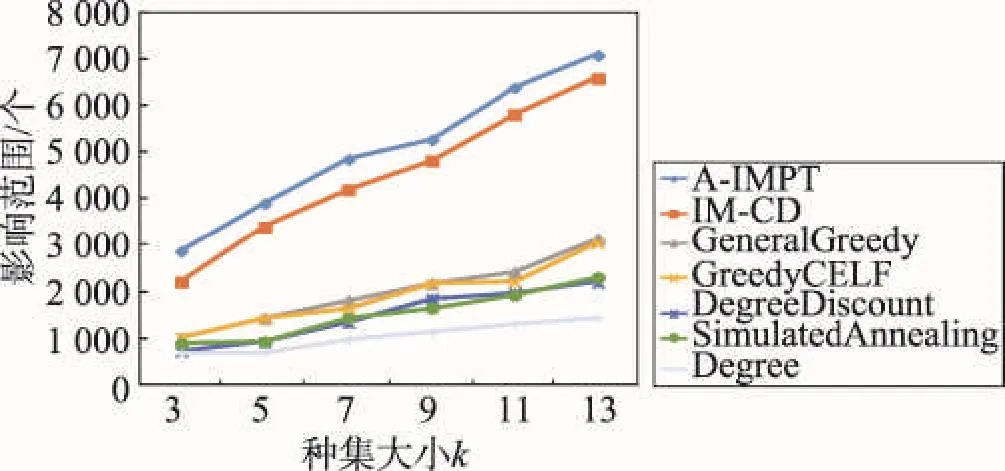
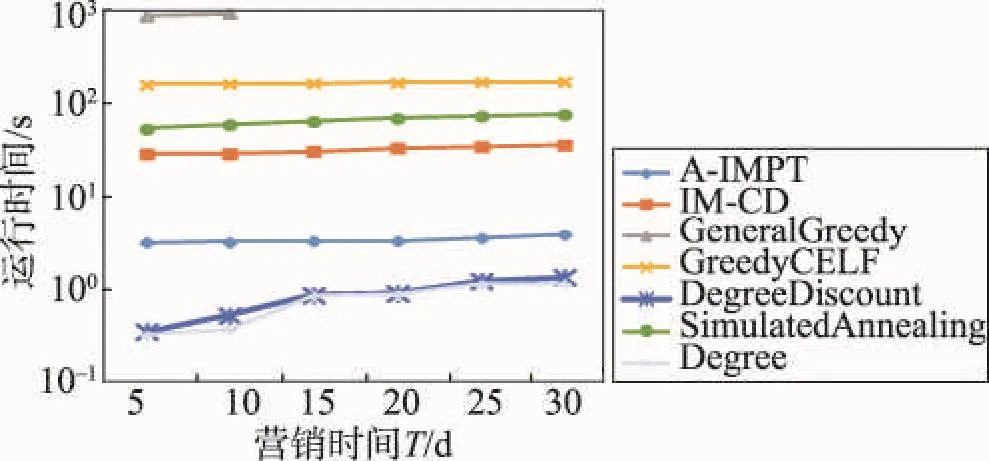
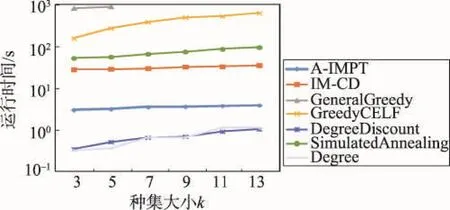
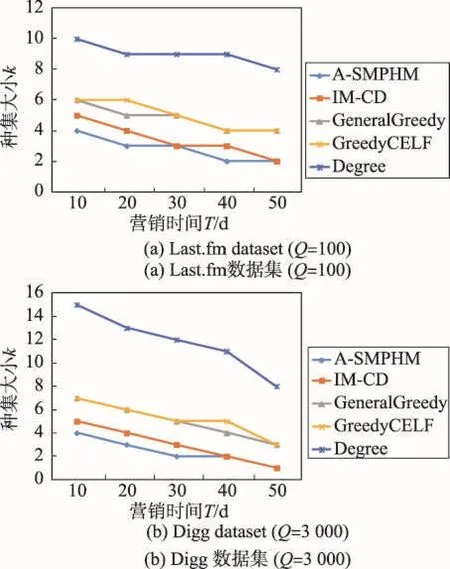
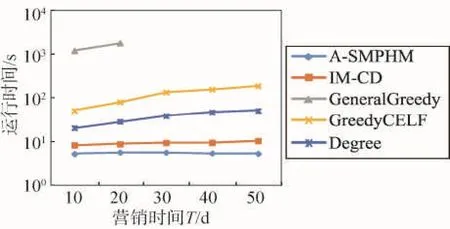
算法2给出了饥饿营销中基于时间的种集最小化问题的算法A-SMPHM，大体思想与算法1相似。为了简便，算法2略去了得到图G′的过程，只给出核心思想。算法第3~4行比较当前种集的影响范围S.mg与输入的期望影响范围Q。如果S.mg

算法2 A-SMPHM算法

输入：社会网G′=(V,E′)，动作日志A，营销时间T，期望的影响范围Q。

输出：T时间内，能够达到期望范围Q的最小种集S。

1. S←∅;

2. (Inde_list ,queue) = parentslink(G′,A);

3. While ( S.mg < Q)

4. S=S⋃CELF(G’,Inde_list,queue,S);

5. Return S;

4.1建立入度链表,更新节点初始影响增益

算法parentslink扫描图G′=(V,E′)，对每个节点建立入度链表Inde_list，扫描动作日志，为每个节点分配影响力。同时计算节点的初始影响增益。

算法（第1~6行）建立入度链表，扫描动作日志，分配影响力。为了方便计算，先将动作日志按照动作进行排序，再按照执行动作的时间进行排序，根据式（7）计算节点之间的直接影响力，之后根据式（9）计算节点之间的间接影响力。因为G′已经根据营销时间处理过，所以可对链表中每个节点迭代地分配直接影响力，然后更新间接影响力。

算法（第7~10行）利用Co-influence算法计算每个节点v∈V的初始影响增益v.mg，利用优先级队列queue，以每个节点的影响增益v.mg为基准进行由大到小排序。并标记计算每个节点v影响增益的轮数v.round为0。具体伪代码如算法3所示。

算法3 parentslink算法

输入：G′=(V,E′)，动作日志A。

输出：每个节点v∈V的影响力值分配链表Inde_list[v]，优先级队列queue。

1. For each v∈V

2.建立节点v的入度链表Inde_list[v];

3. For each u∈Inde_list[v] ;

5. For each w∈Inde_list[u]

7. queue←∅;

8. For each v∈V

9. v.mg =Co-influence(Inde_list,v ,∅);

10. v.round =0; push(queue,v);

4.2 CELF优化选取最大影响增益节点

本节利用CELF优化贪心选取节点。CELF优化利用了InfS的子模性，每一轮不需要重新计算所有节点的影响增益，有效地提高了算法效率。CELF算法分两个阶段。第一阶段（第1~3行）取队列头节点v，如果v的影响增益计算轮数v.round等于当前种集数，则v对当前种集S来说是增益最大的节点。返回v，并利用算法Update更新其他节点u∈VS的影响力入度链表Inde_list，删除所有通过v分配的影响力，同时更新节点u对种集S的影响力分配值Ind。第二阶段（第5~7行）如果v.round不等于当前种集数，说明v的增益v.mg不是针对当前种集S的影响增益。此时利用算法Co-influence重新计算v针对当前种集S的影响增益，更新节点v的影响增益计算轮数v.round，并将节点v重新插入到优先级队列queue，返回第1行重新求增益最大的节点。重复以上过程直到选出一个针对当前种集S具有最大影响增益的节点。具体过程如算法4所示。

算法4CELF算法

输入：社会网G′=(V,E′)影响力值分配链表Inde_list，优先级队列queue，当前种集S。

输出：当前具有最大增益的种子节点v。

1. v = pop(queue);

2. If (v.round == |S|)

3. Update(Inde_list, v, S);

4. Else

5. v.mg = Co-influence(Inde_list, v, S);

6. v.round = |S|; push(queue,v);

7. Goto 1;

8. Return v;

4.3计算节点v针对当前种集S的影响增益

本节采用Co-influence算法计算节点v针对当前种集S的影响增益。算法第5行去除节点v对种集S的影响力分配值Ind，得到节点v对种集S的影响增益v.mg。算法的具体过程如算法5所示。

算法5 Co-influence算法

输入:节点v，影响力分配链表Inde_list，当前种集S。

输出: v针对种集S的影响范围增益v.mg。

1. margin = 0;

2. For each u∈V

3. If (v∈Inde_list[u])

4. margin +=节点u分配给v的影响力;

6. Return v.mg;

4.4更新影响力

当节点v加入种子集合后，本节利用算法Update更新其他节点u∈VS的影响力入度链表Inde_list。算法第2~4行先删除节点u通过v分配的影响力，第5行更新节点u对种集S的影响力分配值Ind。Update算法的具体过程如算法6所示。

算法6 Update算法

输入：节点v，影响力分配链表Inde_list，当前种集S。

输出：影响力分配链表Inde_list。

1. For each u∈V

2. If(v∈Inde_list[u])

3. For each w∈Inde_list[v]

4.删除Inde_list[u]中通过v分给w的影响力;

4.5时间复杂性和近似比计算

A-IMPT和A-SMPHM算法的时间复杂度都为O(|S ||V ||A | γ)，其中|S|为种子节点个数，|V|是图中节点个数，|A|是动作日志记录数，γ是所有节点中祖先节点的最大值max{|Inde_list[u]| ,u∈V}，即最大的Inde_list的长度。

定理3 IM-IMF算法的近似比为1-1/e。

证明当营销时间T为常数时，根据文献[10]的定理2容易证明InfS的子模性和单调性，因此可以用贪心算法找到近似解，近似解和最优解的比值为1-1/e。

5　实验与结果分析

本文在两个社会网数据集上进行实验，并与多种算法进行比较，验证了算法的有效性和高效性。

5.1数据集及实验环境

本文使用两个真实社会网络数据集进行实验，表3给出了数据集的信息。Last.fm[12]是音乐评论网站，本文提取了2 100个节点，25 435条边和动作日志记录。若用户u在时间t评论了歌手a，并且用户u的朋友v在时间t后也评价了歌手a，那么就认为这个动作从u传播到了v。Digg中文翻译为“掘客”，是新闻评论网站，本文提取了35 000个用户，3 905 513条边，其评论传播过程与Last.fm相似。

Table 3　 Last.fm dataset and Digg dataset表3　 Last.fm数据集和Digg数据集

实验中所有算法用C语言编写，在Microsoft Visual C++ 6.0环境下编译。所有实验都在Intel®CoreTM2 Duo CPU，4 GB主存的台式机上运行。

5.2比较算法

实验选择了6种已有的算法和本文A-IMPT算法进行比较，比较算法介绍如下。

（1）IM-CD（influence maximize credit distribution）[14]：利用动作日志，为每个节点在每个动作上建立链表，分配影响力直接求得影响范围，再用CELF优化算法求种集。

（2）GeneralGreedy[3]：贪心方法求种集。

（3）GreedyCELF[5]：CELF优化贪心方法求种集。

（4）DegreeDiscount[6]：启发式度折扣方法求种集。

（5）SimulatedAnnealing[9]：模拟退火法求种集。

（6）Degree：直接根据节点度的大小选择种集。

为了公平比较，以上所有比较算法中都用有效传播时间区间中的进行删图，也就是所有的算法都在图G′=(V,E′)上进行。在本文的所有实验中，如果没有特殊说明，均采用3.1节的AVSV方法计算有效传播时间区间。参考文献[3,5-6,9]中对参数的设置，设置GeneralGreedy、GreedyCELF、SimulatedAnnealing中边上传播概率p=0.1。GeneralGreedy算法中蒙特卡洛模拟次数为R=10 000。在SimulatedAnnealing算法中设置起始温度t0=100，终止温度tf=10，递减温度tm=2。

5.3时间及种集大小对影响范围的影响(AIMPT)算法

本节验证了时间和种集大小对影响范围的影响，并与其他算法比较，验证了A-IMPT算法的有效性。

首先，对不同营销时间下种集的影响范围进行比较。图2（a）给出了A-IMPT算法和6种方法在Last. fm数据集上求得种集影响范围的比较，图2（b）给出在Digg数据集上的比较。其中，设置种集个数k=5。

Fig.2　 Spread and time T in Last.fm and Digg datasets (k=5)图2　在Last.fm和Digg数据集上影响范围与营销时间T(k=5)

从图2可以看出，因为所有算法都利用有效传播时间区间对图G进行了删减，随着时间增加，被删减的图结构越来越少，图G’逐渐增大，所以无论在哪个数据集上，所有算法求得的影响范围都随着营销时间的增加而不断增长，这也是符合真实情景的。其中Degree和DegreeDiscount选取种集的影响范围都比较差，因为这两种算法是完全基于节点的度来计算种集，只考虑节点的度而并不考虑其他因素；General-Greedy、GreedyCELF和SimulatedAnnealing影响范围差别不大，但都远远小于IM-CD和A-IMPT算法，是因为这几种算法只考虑图的拓扑结构，且人为设定边上概率，并不符合真实生活中的情景；IM-CD基于数据求影响范围，但其单纯将分配的影响力设置为1/入度，由于图结构较大，1/入度是很小的数，导致了影响范围也较小，且IM-CD算法并没有考虑时间因素；A-IMPT算法利用真实动作日志分配影响力，经过比较，A-IMPT算法要优于IM-CD算法。

下面考察种集大小对影响范围的影响。图3显示了在Last.fm数据集上，相同营销时间下种子个数不同对影响范围的影响。其中设置营销时间T=10。通过图3可以看出当营销时间T相同时，由于A-IMPT算法利用了真实的动作日志分配了影响力，并迭代更新了节点的影响增益，相比于其他方法，A-IMPT更符合真实情景中对影响力的分配方式，得到了比其他算法更好影响范围。

Fig.3　 Spread and seedsize k in Last.fm dataset (T=10)图3　在Last.fm数据集上影响范围与种子个数k(T=10)

5.4时间及种集大小对运行时间的影响(AIMPT算法)

本节主要比较了时间和种集大小对运行时间的影响，并验证了A-IMPT算法的高效率。

首先固定种集个数k，观察不同的营销时间和运行时间之间的关系。图4是Last.fm数据集上，营销时间T和运行时间之间关系的比较。明显的，General-Greedy使用蒙特卡洛模拟的方法估计影响范围，导致时间非常长，当T>10，图中的绝大部分边都被保留，运行时间超过了1 000 s，且呈指数级上涨，因此图中没有给出，GreedyCELF由于部分过程需要用蒙特卡洛模拟，时间也达到100 s以上；SimulatedAnnealing由于要不断更换种集节点，运行时间也并不理想；IM-CD算法不考虑时间因素，需要扫描每个动作并为每个节点的每个动作建立影响力分配链表，因此IM-CD算法建立了|V|×|A|个链表用来分配影响力，其中|V|是节点个数，|A|是动作日志条数，而动作日志条数往往高达几十万条，这也就导致了运行速度并不理想。而A-IMPT算法提前处理了动作日志，删减了图结构，且只为每个节点分配影响力分配链表，即只建立最多|V|个链表来分配影响力，因此扫描链表的过程中大大提高了时间；DegreeDiscount和Degree算法虽然运行速度比A-IMPT算法快，但是却没有近似比的保证，影响范围远远没有A-IMPT算法好。

Fig.4　 Running time and time T in Last.fm dataset (k=5)图4　在Last.fm数据集上运行时间与营销时间T(k=5)

接下来讨论当营销时间相同时，种集大小与运行时间之间的关系。图5是在Last.fm数据集上，种集大小和运行时间之间的关系比较结果。结合图3和图5可以看到，A-IMPT算法在真实的数据集上获得了理想的影响范围的同时大大减少了运行时间，提高了算法的效率。

本文在Digg数据集上也做了相同的实验，得到了类似的实验结果。由于篇幅有限，这里没有列出。

Fig.5　 Running time and seedsize k in Last.fmdataset (T=10)图5　在Last.fm数据集上运行时间与种集个数k (T=10)

5.5营销时间对种集大小和运行时间的影响(A-SMPHM算法)

由于目前尚没有算法提出解决饥饿营销模式中的影响力传播问题，因此将IM-CD、GeneralGreedy、GreedyCELF和Degree算法进行了调整，并用有效传播时间区间中的?进行了删图（详见算法1）。从而适应本文提出的SMPHM问题，并与A-SMPHM算法进行了比较。实验中，参考文献[3,5-6,9]中对参数的设置，设边上的传播概率p=0.1。蒙特卡洛模拟次数R=10 000。

图6（a）是在Last.fm数据集上固定期望影响范围Q=100，比较营销时间T和选取的最小种子节点个数之间的关系。图6（b）是在Digg数据集上的相同实验。其中设置Q=3 000。从图6中可知，无论在哪个数据集上，固定相同的影响范围和营销时间，ASMPHM算法都比其他方法获得了更小的种集，也就是说A-SMPHM算法有效地获得了更小的初始用户来达到营销中期望达到的影响范围。从而证明了ASMPHM算法的有效性。而从现实生活角度来说，更小的初始用户意味着更低的初期成本和更高的利润，这也是商家希望看到和实现的。

图7是在Last.fm数据集上关于营销时间和运行时间的实验结果。

从图7中可知，A-SMPHM算法效率比General-Greedy算法至少提高3个数量级。Degree算法基于节点的度排序选择种集，运行速度快，但求得的影响范围较差。但SMPHM问题需将每轮影响范围与期望影响范围比较，由于Degree算法不能得到较好的影响范围，导致它需要向种集不断地加入节点以满足期望的影响范围，运行时间并不理想。图6和图7证明了A-SMPHM算法有效解决了饥饿营销中基于时间的种集最小化问题，既以更小的种集达到了期望的影响范围，又达到了理想的效率。

Fig.6　 Time T and seedsize k in Last.fm andDigg datasets图6　在Last.fm和Digg数据集上营销时间T与种集个数k

Fig.7　 Running time and time T in Last.fm dataset (Q=100)图7　在Last.fm数据集上运行时间与营销时间T(Q=100)

5.6比较MMV和AVSV度量方法和准确性

3.1节给出两种计算有效传播时间区间的度量方法，本节实验比较两种度量方法的准确性。为了更好地进行比较，用IM-CD算法作为一个比较算法。首先将Last.fm数据集中的动作按照4:1比例分为训练集和测试集。在训练集中分别使用IM-CD算法和分别加入两种度量的A-IMPT算法得到相应的种集，然后在测试集中求得种集的真实影响范围，设置营销时间T=10。图8给出了在测试集上两种度量方法求得的影响范围的大小。

Fig.8　 Real spread and seedsize k in Last.fm testing set (T=10)图8　在Last.fm测试集上影响范围与种子个数k(T=10)

从图8中可知，在A-IMPT算法中无论是运用最大最小值方法还是平均值+标准差方法都获得了更好的真实影响范围，而IM-CD算法没有考虑时间因素，在测试集中的真实影响范围并不如A-IMPT算法好。比较两种度量方式，平均值+标准差的方法获得了更好的真实影响范围，也就是说，平均值+标准差这种度量的准确性更好。

6　结束语

本文基于真实用户动作日志，确定了用户有效的传播时间区间，并提出了基于时间的影响力分配模型IPAT。根据IPAT模型，本文提出了基于时间的影响力最大化问题（IMPT）以及饥饿营销中基于时间的种集最小化问题（SMPHM），并证明了它们是NP-hard问题。本文提出了求解IMPT问题的有效近似算法A-IMPT，以及求解SMPHM问题的有效近似算法A-SMPHM，并严格证明了A-IMPT和A-SMPHM算法的近似比。多个真实社会网数据集上的实验表明：本文算法能有效并高效求解IMPT问题和SMPHM问题。未来研究工作将考虑基于主题分布和营销时间，对用户之间影响力进行更合理的分配，从而更准确地预测最佳种集。

References:

[1] Domingos P, Richardson M. Mining the network value of customers[C]//Proceedings of the 7th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, San Francisco, USA, Aug 26-29, 2001. New York, USA: ACM, 2001: 57-66.

[2] Kempe D, Kleinberg J, Tardos É. Maximizing the spread of influence through a social network[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, USA, Aug 24-27, 2003. New York, USA:ACM, 2003: 137-146.

[3] Kempe D, Kleinberg J M, Tardos E. Influential nodes in a diffusion model for social networks[C]//LNCS 3580: Proceedings of the 32nd International Colloquium on Automata, Languages and Programming, Lisbon, Portugal, Jul 11-15, 2005. Berlin, Heidelberg: Springer, 2005: 1127-1138.

[4] Kimura M, Saito K. Tractable models for information diffusion in social networks[C]//LNCS 4213: Proceedings of the 10th European Conference on Principles and Practice of Knowledge Discovery in Databases, Berlin, Germany, Sep 18-22, 2006. Berlin, Heidelberg: Springer, 2006: 259-271.

[5] Leskovec J, Krause A, Guestrin C. Cost-effective outbreak detection in networks[C]//Proceedings of the 13th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, San Jose, USA, Aug 12-15, 2007. New York, USA: ACM, 2007: 420-429.

[6] Chen Wei, Wang Yang. Efficient influence maximization in social networks[C]//Proceedings of the 15th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Paris, France, Jun 28-Jul 1, 2009. New York, USA: ACM, 2009: 199-208.

[7] Chen Wei, Wang Chi, Wang Yajun. Scalable influence maximization for prevalent viral marketing in large-scale social networks[C]//Proceedings of the 16th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Wash-ington, USA, Jul 25-28, 2010. New York, USA: ACM, 2010: 1029-1038.

[8] Goyal A, Bonchi F, Lakshmanan L V S. Learning influence probabilities in social networks[C]//Proceedings of the 3th ACM International Conference on Web Search and Data Mining, New York, USA, Feb 3-6, 2010. New York, USA: ACM, 2010: 241-250.

[9] Jiang Qiang, Song Ge, Wang Yang. Simulated annealing based influence maximization in social networks[C]//Proceedings of the 25th Conference on Artificial Intelligence, San Francisco, USA, Aug 7-11, 2011. Menlo Park, USA: AAAI, 2011: 318-326.

[10] Li Hui, Bhowmick S S, Sun Aixin. CINEMA: conformityaware greedy algorithm for influence maximization in online social networks[C]//Proceedings of the 16th International Conference on Extending Database Technology, Genoa, Italy, Mar 18-22, 2013. New York, USA:ACM, 2013: 323-334

[11] Li Guoliang, Chen Shuo, Feng Jianhua, et al. Efficient locationaware influence maximization[C]//Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, Snowbird, USA, Jun 22- 27, 2014. New York, USA:ACM, 2014: 87-98.

[12] Feng Shanshan, Chen Xuefeng, Cong Gao, et al. Influence maximization with novelty decay in social networks[C]// Proceedings of the 28th Conference on Artificial Intelligence, Quebec City, Canada, Jul 27-31, 2014. Menlo Park, USA:AAAI, 2014: 37-43.

[13] Aslay C, Barbieri N, Bonchi F, et al. Online topic-aware influence maximization queries[C]//Proceedings of the 17th International Conference on Extending Database Technology, Athens, Greece, Mar 24-28, 2014: 295-306.

[14] Goyal A, Bonchi F, Lakshmanan L V S. A data-based approach to social influence maximization[J]. Proceedings of the VLDB Endowment, 2011, 5(1): 73-84.

LIU Yong was born in 1975. He received the Ph.D. degree in computer science from Harbin Institute of Technology in 2010. Now he is an associate professor and M.S. supervisor at School of Computer Science and Technology, Heilongjiang University. His research interests include data mining and database, etc.刘勇（1975—），男，河北昌黎人，2010年于哈尔滨工业大学计算机科学专业获得博士学位，现为黑龙江大学计算机科学技术学院副教授、硕士生导师，主要研究领域为数据挖掘，数据库等。

QU Sitong was born in 1992. She is an M.S. candidate at School of Computer Science and Technology, Heilongjiang University. Her research interest is data mining.曲思桐（1992—），女，黑龙江哈尔滨人，黑龙江大学计算机科学技术学院硕士研究生，主要研究领域为数据挖掘。

WANG Nan was born in 1980. She is a Ph.D. candidate at School of Electronic Engineering, Heilongjiang University. Her research interests include sensor network and social network, etc.王楠（1980—），女，黑龙江哈尔滨人，黑龙江大学电子工程学院博士研究生，主要研究领域为传感器网络，社会网络等。

GUO Longjiang was born in 1973. He received the Ph.D. degree in computer science from Harbin Institute of Technology in 2007. Now he is a professor and M.S. supervisor at School of Computer Science and Technology, Heilongjiang University. His research interests include data mining, parallel and distributed computing, etc.郭龙江（1973—），男，河北丰宁人，2007年于哈尔滨工业大学计算机科学专业获得博士学位，现为黑龙江大学计算机科学技术学院教授、硕士生导师，主要研究领域为数据挖掘，并行与分布式计算等。

Research on Time-Based Influence Propagation Methods in Different Marketing Modeƽ

LIU Yong+, QU Sitong, WANG Nan, GUO Longjiang
School of Computer Science and Technology, Heilongjiang University, Harbin 150080, China
+ Corresponding author: E-mail: acliuyong@sina.com

LIU Yong, QU Sitong, WANG Nan, et al. Research on time-based influence propagation methods in different marketing mode. Journal of Frontiers of Computer Science and Technology, 2016, 10(3): 338-349.

Abstract:Influence maximization is the problem of finding a small set of influential users in a social network that maximizes the expected spread. However, the existing works often ignore the effective propagation time interval between uses, and also don’t take influence of the marketing time on the initial seed users into consideration. This paper uses real action log to determine the effective propagation time interval between users, and proposes an influence power allocating model based on time, called IPAT. According to the IPAT model, this paper proposes an influence maximization problem based on time (IMPT) and a seed set minimization problem in hungry marketing (SMPHM), and proves that these two problems are NP-hard. In order to solve IMPT and SMPHM, this paper proposes two effective approximation algorithms, called A-IMPT and A-SMPHM respectively, and theoretically shows that the approximation ratio of the proposed algorithms A-IMPT and A-SMPHM. The experimental results in several datasets on real social networks validate the effectiveness and efficiency of A-IMPT and A-SMPHM.

Key words:social network; influence propagation; propagation time interval; marketing time; hungry marketing

doi:10.3778/j.issn.1673-9418.1507076

文献标志码：A

中图分类号：TP311