带权重条件熵的属性约简算法*
祖鸿娇,米据生
河北师范大学数学与信息科学学院,石家庄050024
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(03)-0445-06
带权重条件熵的属性约简算法*
祖鸿娇+,米据生
河北师范大学数学与信息科学学院,石家庄050024
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(03)-0445-06
E-mail: fcst@vip.163.com
http://www.ceaj.org
Tel: +86-10-89056056
* The National Natural Science Foundation of China under Grant Nos. 61170107, 61300153, 61300121 (国家自然科学基金); the Natural Science Foundation of Hebei Province of China under Grant Nos. A2013208175, A2014205157 (河北省自然科学基金); the Talent Programme of Innovation Team in Colleges and Universities of Hebei Province under Grant No. LJRC022 (河北省高校创新团队领军人才培育计划项目).
Received 2015-05,Accepted 2015-07.
CNKI网络优先出版: 2015-07-03, http://www.cnki.net/kcms/detail/11.5602.TP.20150703.1101.001.html
摘要:粗糙集理论中最重要的内容之一就是属性约简问题,现有的许多属性约简算法往往是基于属性对分类的重要性,如果属性约简的结果能满足用户实际需要的信息,如成本、用户的偏好等,那么约简理论将会有更高的实用价值。基于此,从信息熵的角度定义了带权重的属性重要性,然后重新定义了基于带权重的属性book=1,ebook=150重要性的熵约简算法。最后通过实际例子说明,与基于属性重要性的熵约简算法相比,考虑权重的算法更加符合用户的实际需求。
关键词:粗糙集;条件熵;加权属性重要性;熵约简
1 引言
粗糙集是由Pawlak教授在1982年提出的,用以处理不确定、不精确知识的一种数学理论方法。粗糙集理论[1]在很多领域有广泛的应用,如数据挖掘、机器学习、故障诊断、模式识别[2-5]等。该理论最重要的特点就是它不需要任何先验信息就可以直接从信息系统中提取知识。属性约简是从数据表中获取规则的重要过程,是为了简化原始的信息系统但不影响信息系统的分类能力,从而删除冗余属性的过程,是粗糙集理论中最重要的研究内容之一[6-10]。本文以条件熵为启发知识,对决策表采用启发式知识约简算法,算法的起点是初始条件属性集,采用逐步删除条件属性的方法来得到约简结果。
基于条件熵的属性重要性[11]的属性约简算法是以最少条件属性为出发目标,同样采用启发式原则,令初始的约简属性集为给定的条件属性集,将属性按照其重要性从小到大逐个删除,直到属性集满足约简条件为止。从该约简算法的处理过程可以看出,通过这种算法确实可以得到最小的属性集,然而其得到的约简结果却忽视了如成本、用户的偏好等实际需要,缺乏实际应用价值。2014年重庆大学的张清华和沈文在文献[12]中研究了这类问题,提出了考虑用户需求的加权属性重要性,并给出了一种新的属性约简算法,与本文不同的是,其算法采用的是正域约简。
在现实生活中,人们往往是为了满足自身需求而进行某些社会活动。在粗糙集的熵约简中,用户已经有了每个属性的先验知识,如用户的偏好,而这些先验信息并不能反映其对属性集合的分类能力,而属性的重要性也只反映了其对属性集合的分类能力,并不能反映用户的偏好需求。因此需要通过添加一个权重系数将这两个要求结合起来,并通过调整系数的大小来反映用户对这两个要求的倾向程度。这样,根据重新定义的加权属性重要性设计出一个新的熵约简算法,通过该算法来得到更满足用户需求的属性约简。
2 预备知识
定义1[13](目标信息系统)目标信息系统被定义为一个四元组S=(U,C⋂D,V,f),其中U是研究对象的非空有限集合,也称为论域,U={x1,x2,⋂,xn}; C⋂D称为属性集, C是条件属性集,D是决策属性集;V是属性值的集合;f:U×C⋂D→V称为信息函数,它指定U中每一个对象的属性值。
定义213](不可辨识关系)对于条件属性集C或决策属性集D的一个子集B,有一个U上的不可辨识关系,如果(x,y)属于RB,就说x和y是B不可辨识的。以这种方法定义的不可辨识关系是等价关系。不可辨识关系RB的所有等价类的集合记作,包含元素x的等价类记作。
定义3[14](信息熵)设U是一个论域,属性集合B 在U上的划分为X={X1,X2,⋂,Xn},属性集合B的熵H(B)定义为H(B)=
定义4[15](条件熵)属性集A(U/A={Y1,Y2,⋂,Ym})相对于属性集B(U/B={X1,X2,⋂,Xn})的条件熵H(A|B)定义为H(A|B)=,其中i=1,2,⋂,n,j=1,2,⋂,m。特别地,当Yj⋂Xi=Ø, 即p(Yj|Xi)=0时,定义lb p(Yj|Xi)=0;当属性集B为空集时,H(A|Ø)=1。
定义5[15](熵约简)对于目标信息系统S=(U, C⋂D,V,f),其中U是论域,C是条件属性集,D是决策属性集。对于B⊆C,如果有H(D|B)=H(D|C),则称B为一个熵协调集,若对于B的任何真子集B′,都有H(D|B′)≠H(D|C),则称B为C的一个熵约简。
3 带权重的熵约简算法
3.1带权重的熵约简标准
对于已有的约简算法来说,大多数的约简标准都是为了得到最小的属性集合,而本文则是通过添加一个权重系数,将最少的属性和更满足用户需求的结果作为约简的标准,这样便能得到更具有实际应用价值的研究结果。然而对于不同的用户,其对上述两个标准的倾向程度也存在着差异,可以通过设置不同的权重系数来达到相应的目的。下面就给出属性权重的定义。
定义6(属性权重)对于目标信息系统S=(U, C⋂D,V,f),其中U是论域,C是条件属性集,D是决策属性集。令ti是属性ai的成本值,其中i=1, 2,⋂,n。∀ai∈C,它的属性权重定义为qi=1-ti/j。
属性重要性是研究约简问题时一个关键的概念,文献[7]所用到的属性重要性的概念是一个基于正域的度量,本文定义的属性重要性是基于条件熵的度量。下面给出基于条件熵的属性重要性的概念。
定义7(基于条件熵的属性重要性)对于目标信息系统S=(U,C⋂D,V,f),其中U是论域,C是条件属性集,D是决策属性集,且A⊂C,则对于任意属性a∈C-A的重要性SGF(a,A,D)定义为SGF(a,A,D)= H(D|A)-H(D|A-{a})。
当A为空集时,SGF(a,Ø,D ) =1-H(D|a ) , SGF(a,A,D )的值越大,说明在已知属性子集A的情况下属性a对于决策D越重要。根据上述定义还可以看出,当属性子集A发生改变时,所有属性的重要性也发生相应的变化,也就是说属性的重要性和属性子集是密切相关的。下面利用表1进行说明,表中第一行表示用户所支付的成本。
当属性子集是空集时,根据定义4和定义7, U/{a}={{x1,x7},{x2,x3,x4,x5,x6,x8}},则属性a的重要性为:
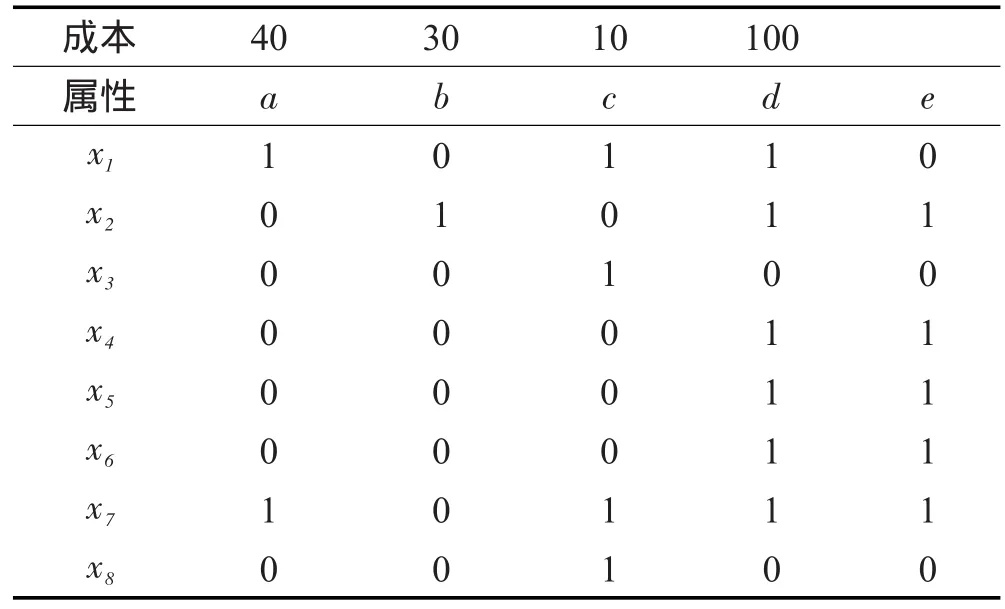
Table 1 Decision information system表1 目标信息系统
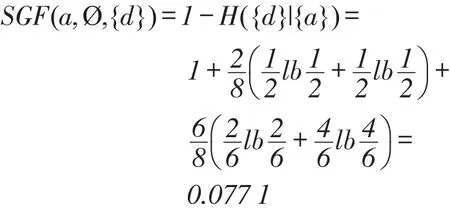
当属性子集为{b,c}时,U/{b,c}={{x1,x3,x7,x8},{x2}, {x4,x5,x6}},U/{a,b,c}={{x1,x7},{x2},{x3,x8}{x4,x5,x6}},则属性a的重要性为:
SGF(a,{b,c},D)=H(D|{b,c})-H(D|{a,b,c})=
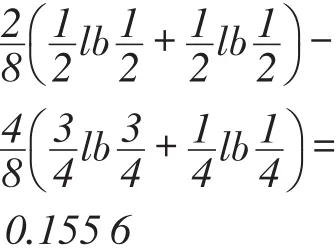
根据上述计算结果可以知道,由于属性子集的改变,属性的重要性也随之改变,从而属性的重要性是动态变化的。在下面定义的算法中,在每一次的循环过程中属性的子集都发生了改变,因此要注意每一次循环都需要重新计算属性的重要性度量。
上面已经有了基于条件熵的属性重要性以及熵约简的概念,下面给出基于属性重要性的熵约简的具体算法。
算法1基于属性重要性的熵约简算法
输入:一个目标信息系统S=(U,C⋂D,V,f),C和D分别为条件属性集和决策属性集。
输出:该目标信息系统的一个熵约简B。
(1)计算目标信息系统S中决策属性D相对条件属性C的条件熵H(D|C);
(2)初始化B=C , A=Ø,计算每个条件属性的重要性SGF(ai,A,D),其中, ai∈C,将ai按SGF(ai,A, D)升序排列;
(3)按SGF(ai,A,D)升序依次选出ai,令B= B-ai,A=A⋂ai,如果B=Ø,则终止循环;
(4)计算条件熵H(D|B-{ai}),如果H(D|C)= H(D|B-{ai}),则停止循环,否则跳到步骤(2);
(5)对于B中每个属性,如果它的属性重要性SGF(ai,B-{ai},D)=H(D|B-{ai})-H(D|B)=0,则删除这个属性,否则就保留,那么此时的B就是约简结果。
3.2基于带权重的属性重要性的熵约简算法
定义8(带权重的属性重要性)考虑目标信息系统S=(U,C⋂D,V,f),其中U是论域,C是条件属性集,D是决策属性集。∀ai∈C,它的加权属性重要性定义为Si=kqi+(1-k)SGF(ai,A,D),其中,qi是属性权重, SGF(ai,A,D)是属性重要性,k为属性权重和属性重要性的权重系数,系数k可以根据用户的需求来设定。当k=0时,加权属性重要性就成了属性的重要性,相应的约简算法就是算法1给出的基于属性重要性的熵约简算法,并且最终得到的约简是具有最少属性的约简。当k=1时,加权属性重要性变成了属性的权重,相应的约简算法是基于权重的属性约简算法,即将算法1中的属性重要性换成属性的权重,这样最终获得的约简更符合用户的需求,即用户支付最少的成本。当0 下面给出综合考虑约简属性的数量以及用户需求的带权重的属性重要性的熵约简算法。 算法2基于带权重的属性重要性的熵约简算法 输入:一个信息系统S=(U,C⋂D,V,f),C和D分别为条件属性集和决策属性集。 输出:该目标信息系统的一个熵约简B。 (1)B初始化,B=C , A=Ø,根据用户的需求调整权重系数k的取值; (2)计算目标信息系统S中决策属性D相对条件属性C的条件熵H(D|C); (3)计算A中每个属性的加权属性的重要性Si=kqi+(1-k)SGF(ai,A,D),初始化SGF(ai,A,D)=1-H({d}|{ai}); (4)选择最小加权属性重要性的属性ai, B= B-ai,A=A⋂ai,如果B=Ø,则跳到(6); (5)如果H(D|C)=H(D|B-{ai}),则循环停止, B是初始的约简,否则跳到步骤(3); (6)对于B中每个属性,如果它的属性重要性SGF(ai,B-{ai},D)=H(D|B-{ai})-H(D|B)=0,则删除这个属性,否则就保留,那么此时的B就是最终的约简。 该算法输出的约简结果B在满足约简条件的同时又能减少用户的支付成本,这是和用户需求一致的。需要注意的是每一次循环步骤(3)时,每个属性的加权属性重要性都应该重新计算。 3.3算法的完备性分析 根据熵约简的定义,如果B⊆C是一个给定的目标信息系统的条件属性的约简,应满足下列条件: (1)H(D|B)=H(D|C); (2)对于B的任何真子集B′, H(D|B′)≠H(D|C)。 如果约简算法同时满足条件(1)和(2),那么这个属性约简算法就是完备的。条件(1)表明属性子集B是一个协调集,这也是属性约简的最基本的要求。条件(2)表明通过该算法得到的约简没有多余的属性,去掉协调集B中的任一属性后都会导致约简的可辨识关系的改变。 定理1基于加权属性重要性的属性算法是完备的。 证明先看条件(1),因为算法2的结束条件是(1),所以由算法2得到的约简一定满足条件(1)。步骤(6)中属性的重要性度量等于0的属性是删除的,根据定义7,在步骤(6)中并不存在冗余的属性,因此条件(2)是满足的。从上面的分析可以得出这样的结论:基于加权属性的重要性的熵约简算法是完备的。□ 例1以表1为例,表中数据量化用户的需求为成本属性,这个成本属性与用户的需求逆相关,即成本值越大,用户对其需求性就越小。 分别根据算法1和算法2计算各自的熵约简,这里取k=0.6,其中C={a,b,c,d}为条件属性,D={e}为决策属性。根据表1 U/C={{x1,x7},{x2},{x3,x8}, {x4,x5,x6}},U/D={{x1,x3,x8},x2,x4,x5,x6,x7}。 首先根据属性重要性算法计算信息系统的属性约简,这里定义初始集为空集,根据定义7,SGF(a, Ø,D)=0.061 3,SGF(b,Ø,D)=0.137 9 , SGF(c,Ø,D)= 0.594 4,SGF(d,Ø,D)=0.512 5,因此选取属性a,则B={b,c,d}。容易验证此时H(D|B)= H(D|C),则循环停止,进行步骤(5)时可以计算出属性b的重要性为0,其余属性都不为0,因此只删除b,最终约简为B={c,d}。 基于算法2,根据定义6,每个条件属性的权重分别为a=0.777 8,b=0.833 3,c=0.944 4, d=0.444 4。在第一轮循环中,每个加权属性重要性分别为a=0.491 2,b=0.555 1,c=0.804 4,d=0.471 6,因此挑出属性d,即B=B-{d}={a,b,c}。容易验证此时H(D|B)=H(D|C),循环停止,并且在进行步骤(6)时可以得到属性b的属性重要性为0,其余均不为0,故删掉b,因此最终约简为B={a,c}。 通过分析可以看出,约简算法2计算所得的总成本是5,约简算法1中所得的总成本是11。算法2的总成本比算法1的总成本要少,说明算法2更符合用户的需求。 本文提到的算法1将原始的属性重要性定义为基于条件熵的属性重要性,算法2将基于熵的属性重要性和量化后的用户需求相结合,也就是先验知识和客观要求的结合,提出了更符合用户需求的新算法。容易看出当算法2中的权重系数k为0时,该算法就是算法1。算法2改进了原始的约简算法,使其更接近现实生活,尤其是对专家系统和医疗诊断系统等现实问题的发展更具有指导性的意义,这也将促进粗糙集理论在现实生活中的应用。 References: [1] Pawlak Z. Rough sets[J]. International Journal of Computer and Information Sciences, 1982, 1115: 341-356. [2] Pawlak Z, Grzymala-Busse J, Slowinski R, et al. Rough sets[J]. Communications of the ACM, l995, 38(11): 89- 95. [3] Lingras P J, Yao Yiyu. Data mining using extensions of the rough set model[J]. Journal of the American Society for Information Science, 1998, 49(5): 415-422. [4] Tsumoto S. Automated discovery of positive and negative knowledge in clinical databases based on rough set model[J]. IEEE EMB Magazine, 2000, 19(4): 56-62. [5] Ziako W C. Rough sets: trends, challenges, and prospects: rough sets and current trends in computing[M]. Berlin: Springer-Verlag, 2001. [6] Duentsch I, Gediga G. Uncertainty measures of rough set prediction[J].Artificial Intelligence, 1998, 106(1): 109-137. [7] Dai Jianhua, Li Yuanxiang, Liu Qun. A hybrid genetic algorithm for reduct of attributes in decision system based on rough set theory[J]. Wuhan University Journal of Natural Sciences, 2002, 7(3): 285-289. [8] Du Yong, Hu Qinghua, Zhu Pengfei, et al. Rule learning for classification based on neighborhood covering reduction[J]. Information Sciences, 2011, 181(24): 5457- 5467. [9] Dai Jianhua, Xu Qing. Attribute selection based on information gain ratio in fuzzy rough set theory with application to tumor classification[J]. Applied Soft Computing, 2013, 13 (1): 211-221. [10] Xu Weihua, Li Yuan, Liao Xiuwu. Approaches to attribute reductions based on rough set and matrix computation in inconsistent ordered information systems[J]. Knowledge Based Systems, 2012, 27: 78-91. [11] Wang Guoyin, Yu Hong, Yang Dachun. Decision table reduction based on conditional information entropy[J]. Chinese Journal of Computers, 2002, 25(7): 759-762. [12] Zhang Qinghua, Shen Wen. Research on attribute reduction algorithm with weight[J]. Journal of Intelligent & Fuzzy Systems, 2014, 27(2): 1011-1019. [13] Zhang Wenxiu, Liang Yi, Wu Weizhi. Information system and knowledge discovery[M]. Beijing: Science Press, 2003: 42-48. [14] Zhang Wenxiu, Liang Yi, Xu Ping. Uncertainty reasoning based on inclusion degree[M]. Beijing: Tsinghua University Press, 2007: 43-49. [15] Dai Jianhua, Wang Wentao, Tian Haowei, et al. Attribute selection based on a new conditional entropy for incompletedecision systems[J]. Knowledge Based System, 2013, 39: 207-213. 附中文参考文献: [11]王国胤,于洪,杨大春.基于条件信息熵的决策表约简[J].计算机学报, 2002, 25(7): 759-762. [13]张文修,梁怡,吴伟志.信息系统与知识发现[M].北京:科学出版社, 2003: 42-48. [14]张文修,梁怡,徐萍.基于包含度的不确定推理[M].北京:清华大学出版社, 2007: 43-49. ZU Hongjiao was born in 1990. She is an M.S. candidate in mathematics at Hebei Normal University. Her research interests include rough set and approximate reasoning, etc.祖鸿娇(1990—),女,河北秦皇岛人,河北师范大学数学专业硕士研究生,主要研究领域为粗糙集,近似推理等。 MI Jusheng was born in 1966. He received the Ph.D. degree in applied mathematics from Xi’an Jiaotong University in 2003. Then he was a post-doctoral fellow at the Chinese University of Hong Kong. Now he is a professor and Ph.D. supervisor at Hebei Normal University. His research interests include rough sets, concept lattices and approximate reasoning, etc.米据生(1966—),男,河北宁晋人,2003年于西安交通大学应用数学专业获得博士学位,随后在香港中文大学从事博士后研究,现为河北师范大学教授、博士生导师,主要研究领域为粗糙集,概念格,近似推理等。 Attribute Reduction Algorithm Based on Conditional Entropy with Weightsƽ ZU Hongjiao+, MI Jusheng ZU Hongjiao, MI Jusheng. Attribute reduction algorithm based on conditional entropy with weights. Journal of Frontiers of Computer Science and Technology, 2016, 10(3): 445-450. Abstract:Attribute reduction is one of the most important contents of rough set theory, and many of the existing reduction algorithms are often based on attribute importance. If the result of attribute reduction can meet the information of actual need, such as the costs and users’preference, etc, the theory of reduction will have higher practical value. So, this paper defines the attribute importance with weights based on information entropy, then defines attribute entropy reduction algorithm which is based on the attribute importance with weights. Finally, the experimental results show that, compared with the entropy reduction algorithm based on the attribute importance, the algorithm with weights is more coincident with the actual requirements of users. Key words:rough set; condition entropy; weighted attribute importance; entropy reduction doi:10.3778/j.issn.1673-9418.1506013 文献标志码:A 中图分类号:O2364 结束语


College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang 050024, China
+ Corresponding author: E-mail: zuhongjiao5@163.com

