求解FFS问题的混合搜索机制粒子群算法*
张海月,秦永彬,许道云
贵州大学计算机科学与技术学院,贵阳550025
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(03)-0433-12
求解FFS问题的混合搜索机制粒子群算法*
张海月,秦永彬,许道云+
贵州大学计算机科学与技术学院,贵阳550025
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(03)-0433-12
E-mail: fcst@vip.163.com
http://www.ceaj.org
Tel: +86-10-89056056
* The National Natural Science Foundation of China under Grant Nos. 61262006, 61540050 (国家自然科学基金); the Major Applied Basic Research Program of Guizhou Province under Grant No. JZ20142001 (贵州省重大应用基础研究项目); the Science and Technology Foundation of Guizhou Province under Grant No. LH20147636 (贵州省科技厅联合基金); the Scientific Research Project of Introduce Talents of Guizhou University under Grant No. 201114 (贵州大学引进人才科研项目); the Graduate Student Innovation Fund of Guizhou University under Grant No. 2015013 (贵州大学研究生创新基金).
Received 2015-10,Accepted 2015-12.
CNKI网络优先出版: 2015-12-02, http://www.cnki.net/kcms/detail/11.5602.TP.20151202.1452.004.html
Key words: flexible flow shop; scheduling algorithm; particle swarm; simulated annealing algorithm
摘要:针对柔性流水车间调度(flexible flow shop scheduling,FFS)问题,提出了一种混合搜索机制粒子群算法(multi-search mechanism particle swarm optimization algorithm,MMPSO),以期获得柔性流水车间调度问题的优化解。在分析柔性流水车间调度问题特点的基础上,设计了针对该问题的粒子信息编码方案,提出了瓶颈机器消除算法以提升初始种群的质量;同时在个体极值搜索中采用NEH-Greedy搜索算法,在全体极值搜索中采用SADA(simulated snnealing disturb algorithm)搜索算法以扩大搜索范围,提高可行解质量,加快收敛速度,在算法迭代搜索过程中对全体极值进行RPA(random perturbation algorithm)操作以避免算法陷入局部最优。实验结果表明,MMPSO算法能够以较快的收敛速度获得柔性流水车间调度问题的一个较好的优化解。
关键词:柔性流水车间;调度算法;粒子群;模拟退火算法
1 引言
流水车间调度问题是由生产制造业引出的规划问题,是确保快速、有效和平稳生产的关键。柔性流水车间调度问题(flexible flow shop scheduling problem)[1-2]是传统流水车间调度问题的延伸与推广,其与传统流水车间调度问题的最大区别是允许工件在一个或多个加工工序中存在并行机,在存在并行机的工序中,工件可任意选择一台并行机加工且加工时间不同,其是一种更加一般化的组合优化问题。在实际生产过程中,多数生产场景都具有柔性流水车间的特点,如化工制造、钢铁铸造、纺织制造等。
柔性流水车间调度问题已被证明是NP-难的[3-4]。针对流水车间调度问题,许多研究者进行了深入的研究,提出了求解此类问题的数学规划方法、启发式算法[5]和智能优化算法[6]。其中,数学规划方法中主要有分支定界法[7]、拉格朗日松弛法[8]、整数规划[9]等,这类方法虽然能给出问题的最优解,但只适用于求解小规模的问题,对于大规模问题的求解会导致指数级的时间开销,无法在实际生产过程中使用。启发式算法通过学习策略寻求最优解,算法运行速度快,能在短时间内得到可行解,在研究与实际生产中得到广泛应用,但可行解质量与最优解的偏离程度是不可预知的,甚至会产生较大的偏差。而近年来兴起的智能优化算法[10]在评价机制基础上通过不断迭代搜索来获得最优解,此类算法虽不能保证得到最优解,但能在可接受的时间范围内得到较好的次优解。常用的智能优化算法包括粒子群算法[11-12]、遗传算法[13]、禁忌搜索算法[14]和模拟退火算法[15]等。近年来众多学者对智能优化算法进行了广泛研究,在系统控制、人工智能、模式识别、生产调度等领域该算法得到迅速推广和应用。在流水作业调度问题研究中,Zandieh等人利用免疫算法[16]增强种群多样性,优化了带依赖序列装载时间约束的混合流水车间调度问题解的质量,并给出了该问题的下界;Mastrolilli等人提出了一种能扩大搜索邻域范围的禁忌搜索算法[17],得到了柔性流水车间调度问题的更好的近似可行解;沈斌等人[18]提出了一种新型的自适应遗传算法,采用初始种群复合化,适应度相同个体的筛选策略以及改进自适应交叉变异概率等方法优化了柔性流水车间调度问题的求解。但大部分学者在柔性流水车间调度问题的研究中,对智能优化算法的改进都集中在扩大搜索范围上,并未对同一台并行机加工工件排序进行优化,在同一台机器上工件之间合适的加工顺序可使下一阶段加工任务的开始时间得以提前,进而提高工作效率,减小工件最大完成时间,优化可行解质量。
本文结合柔性流水车间调度问题的特点,提出了混合搜索机制粒子群算法(multi-search mechanism particle swarm optimization algorithm,MMPSO),用以求解多阶段柔性流水车间调度问题。基于粒子群算法容易理解,实现方便且搜索能力强的特点,MMPSO算法结合粒子群算法的思想,首先设计相应的粒子信息编码方案,根据平均分配机器原则产生较优的初始粒子种群,同时在粒子群全局搜索中增加两种搜索方法增强粒子搜索能力,优化同一台并行机上工件加工顺序,以凹函数惯性权重为参数更新方法加快粒子群收敛速度,算法在执行过程中将对全体极值进行随机扰动避免陷入局部最优,以帮助粒子跳出局部最优。
2 问题描述
柔性流水车间调度问题可描述为:n个工件{J1,J2,⋮,Jn}需要在m道工序上加工,所有工件的加工路线相同,在第i道工序中包含Si台并行机(Si>0⋮,i∈{1,2,⋮,m}),所有工件的第i道工序均可在Si中的任意一台并行机i上加工,所有工件在并行机上加工的时间可以不同。Cij表示工件Ji的工序j的完成时间,Ci表示工件Ji的加工完成时间。该问题假设如下:
(1)所有工件加工路径相同,加工顺序固定;
(2)各个工件没有优先级限制,即工件间加工顺序不受限;
(3)所有机器均可在时间0开始加工;
(4)每个工件的每道工序仅可在一台机器上加工;
(5)每台机器同一时间只能加工一个工件;
(6)工件一旦开始加工不能中断;
(7)机器无故障等特殊情况。
问题的优化目标是最小化最大完成时间(Makespan),即:
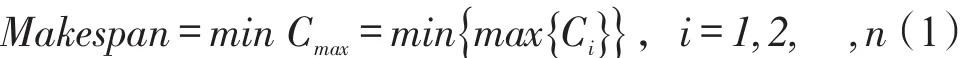
3 混合搜索机制粒子群算法
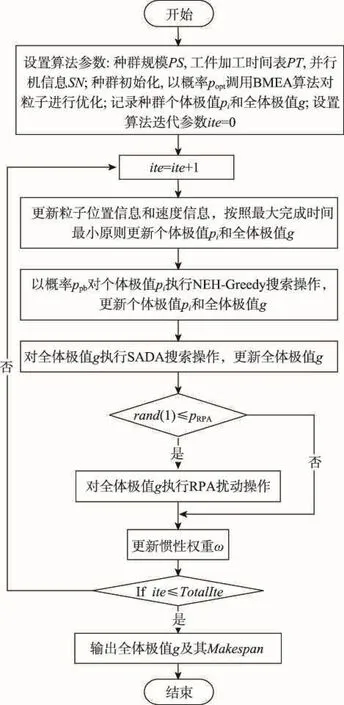
为了将粒子群算法运用于柔性流水车间调度问题的求解,首先需要解决的是解的编码问题。柔性流水车间调度问题中各个工件需要在所有加工工序上选择加工机器,常用的编码方式变得不再适用,因此本文提出了一种矩阵编码方式用于存储可行调度解信息,将粒子信息以行向量的方式存储在矩阵中。标准的粒子群算法的初始化种群随机生成,本文在解空间内初始化粒子信息,并对某些粒子的初始位置信息进行优化操作以提高初始种群的质量。粒子在每次迭代搜索中根据自己和群体飞行经验不断更新位置信息和速度信息,向最优位置靠近。本文在保证可行解合法性的前提下,以叉乘方式更新粒子的位置和速度信息。此外,为扩大粒子群搜索范围,提高算法质量,本文提出了NEH-Greedy搜索算法,以一定概率对个体极值进行优化操作以扩大全体极值的搜索范围。为避免粒子群算法陷入局部最优,对长期处于停滞状态的全体极值增加随机扰动操作,使其跳出停滞状态。下面,将详细介绍MMPSO算法的各个具体步骤。
3.1 MMPSO算法编码方式
柔性流水车间调度问题中每个工件需要指定在每一道加工工序上加工的机器及各并行机上的加工顺序,因此该问题的一个可行解具有两个属性:机器选择和加工顺序。单一的顺序存储不能满足柔性流水车间调度问题可行解的表示,本文采用矩阵编码方式。假设有n个工件{J1,J2,⋮,Jn}待加工,每个工件需要经过m道加工工序{S1,S2,⋮,Sm},第i道工序有Si台并行机。那么该问题的一个可行调度方案如下:
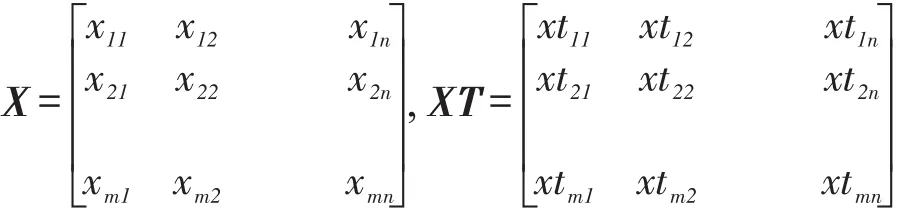
其中,X为机器选择矩阵,XT为加工顺序矩阵。矩阵中,xij⋮(1≤i≤m,1≤j≤n)表示工件Jj在第i道工序上的加工机器编号。若xij=xik⋮, j≠k,表示工件Jj在第i道工序所选择加工机器相同。xtij表示工件Jj在第i道工序加工机器上的顺序编号。
工件在每台机器上的加工时间同样采取矩阵存储,每道工序i存在Si台并行机,为方便计算,将机器按照工序依次编号为1,2,⋮,λ。对任意工序k⋮(⋮1≤k≤m),其并行机Mπ的编号π的取值范围可控制为:
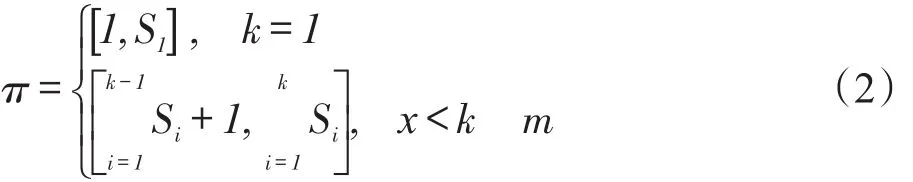
例1某柔性流水车间调度问题中包含5个待加工工件,每个工件有4道加工工序,每道工序的并行机数量分别为2、1、2、3,那么各阶段机器编号分别为{1,2}、{3}、{4,5}、{6,7,8}。一个可行的调度方案如下:
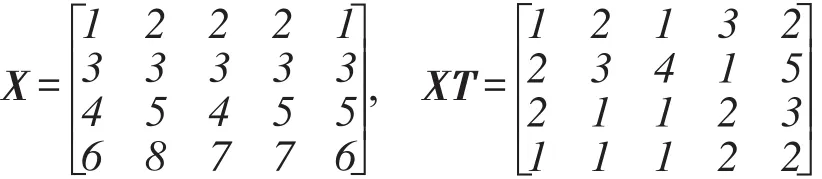
其中,x31=x33=4表示工件J1和工件J3的第三道工序均在机器M4上加工;而由矩阵XT可知,xt31=2,xt33=1,这表明在机器M4上工件J3第一个加工,工件J1第二个加工。
MMPSO算法中每个粒子表示柔性流水车间调度方案的一个可行解,柔性流水车间调度问题的一个可行解具有两个属性,机器选择和加工顺序,因此每个粒子信息也包含以上两个属性。而标准粒子群算法中粒子信息为行向量,以矩阵方式存贮粒子群信息,因此需要将矩阵X和XT分别转换为m×n维行向量O和OT以表示粒子信息:
O=[o1,o2,⋮,om×n], OT=[ot1,ot2,⋮,otm×n]
原调度信息矩阵X(机器选择)中xij转换为粒子信息or,其中r=(j-1)×m+i。同理,原调度信息矩阵XT(加工顺序)中xtkl转换为粒子信息otq,其中q=(l-1)×m+k。
对于第一道加工工序,即⋮k=1⋮,机器编号控制为[1,第一道工序S1并行机数量]。对于非第一道工序,即k≠1,机器编号控制为[前k-1道工序并行机数量之和加1,前k道工序并行机数量之和]。
根据以上编码方式,本文求解Makespan只需对m道加工工序中所有待加工的n个工件计算加工开始时间和结束时间,那么计算Makespan的时间复杂度为O(mn)。
3.2种群初始化
种群初始化是MMPSO算法的起点,一个可行解包含机器选择和加工顺序这两个属性,因此需要同时初始化粒子的以上两种信息。机器选择信息需要在由式(2)表示的每道工序可选机器编号范围内随机产生初始粒子信息,以保证随机产生的调度方案的可行性。例如:对于一个调度方案的机器选择信息O中or代表工件Jj在第i道工序的加工机器(i=(r-1)mod⋮m+1,j=ë(r-1)/m û +1),则初始化为:
粒子加工顺序OT初始化为值全为1的向量。根据粒子的机器选择信息修改加工顺序OT。具体方法为:首先将粒子的机器选择信息O转化为调度矩阵X=[xij]m×n,然后按以下方法确定OT的值。
(1)xij=xik⋮,j≠k,i若为第一道加工工序,即i=1,则工件排序按照其加工时间的升序排列;
(2)若不为第一道加工工序,即i≠1,则按照每个工件前一道工序的完成时间升序排列来确定加工顺序。
由于随机产生的调度方案具有较大的不确定性,在某个粒子的调度排序中可能出现瓶颈机器(即在同一工序上较多工件都选择在同一台机器加工且加工总时间较长,此类机器为瓶颈机器),而其他并行机空闲的状况,此类情况会影响寻优的速度和解的质量。为提高寻优速度,解决产生瓶颈机器的问题,同时为保证粒子种群的多样性,在粒子群中以概率popt对粒子的初始位置信息进行优化操作。本文采用以下瓶颈机器消除算法(bottleneck machine elimination algorithm,BMEA)优化粒子初始位置信息。
算法1 BMEA算法
Input:一个柔性流水车间可行解Sch Output:无瓶颈机器可行解Sch
2. CountSame( ) i←计算每台机器上加工工件数
3. N←可行调度Sch各机器加工工件数
4. w=1←标记
5. for k=1,2,⋮,m
6. while w=1
15. else
16. w=0
17. end
18. end
19. end
20. return Sch
BMEA算法中,需要遍历每一道工序,其复杂度为O(m);对于工序i,最坏情况为所有工件都在同一台机器上加工,最多需要对n-2个工件的加工机器信息进行修改,时间复杂度为O(n)。因此算法BMEA的时间复杂度为O(mn)。
3.3粒子位置及速度信息更新
由于柔性流水车间调度问题的特殊性,粒子位置和速度信息需要合法性检测,基本粒子群更新方法不再适用,需要对粒子的位置和速度更新公式进行改进,修改后的粒子速度更新公式为:
其中,vti+1和vti分别表示粒子i在t+1和t时刻的速度信息;ω为惯性权重;pi是粒子i当前个体极值;g为当前粒子群全体极值;c1,c2∈{ } 0,1;⊗为叉乘操作,若差乘操作对象为零矩阵则取消该项。ω采用递减凹函数策略更新。算法初期,粒子需要较大的自我认知,而后期则需要较大的社会认知,才不会使算法陷入局部最优,加快收敛速度。因此,算法以概率ω选取c1=1,c2=0,否则选取c1=0,c2=1。以ω为比重计算交换列数r(1≤r≤n),随机产生r个交换列,列交换后产生两个新的调度方案,更新较优调度为粒子新时刻速度信息。
相应修改后的粒子位置信息更新公式为:
例2图1中,规模为3×5的个体a1和a2信息,计算a1⊗a2。算法产生随机交叉点r=2,即分别交换第1~2列和第3~5列的位置信息,交叉操作后所得新个体信息为b1和b2。其中b1为a1的1~2列信息与a2的3~5列信息的连接;b2为a1的3~5列信息与a2的1~2列信息的连接。分别计算b1和b2的最大完成时间,取最大完成时间最小排序为a1⊗a2的运算结果。
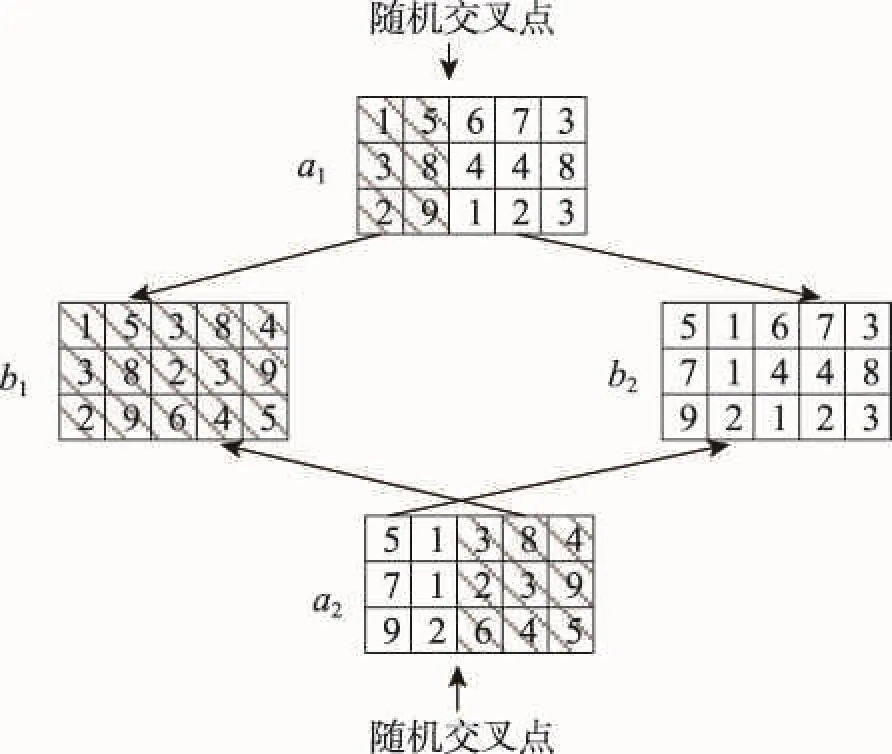
Fig.1 An example of article information updates图1 粒子信息更新举例
3.4 NEH-Greedy搜索算法
基本NEH算法是求解置换流水车间调度问题的效率较高的启发式算法,其赋予加工时间越长的加工优先权,由此优先权取得初始排列,通过插入方法构造一个调度。贪心算法是近似算法中常用的简单方法,该算法对问题求解时,总是做出当前最优解选择,可称局部最优解选择。
在柔性流水车间调度问题中,每个工件在每道加工工序的并行机上加工时间不同,很难对工件进行总时间排序和分别插入操作,因此将在同一机器上工件加工顺序视为传统流水车间调度问题中的某一加工阶段,采用NEH算法得到较好的局部排序。同时结合贪心算法获取当前最优的特点,本文提出NEH-Greedy搜索算法,优化粒子个体极值。算法中,对于一个可行解,首先计算需要加工多个工件的机器集合ψ,取集合ψ中的第一台机器φ1,按待加工工件加工时间升序排列,将排序后的工件前后平均分成两组α1和α2,构成两种子排序{α1,α2}和{α2,α1},产生两个新可行解;评价新可行解与原可行解,保存较优排序为当前最优解;若ψ≠∅,对于ψ中下一台机器重复以上操作,否则算法结束,输出优化解。具体算法描述如下。
算法2 NEH-Greedy搜索算法
Input:一个柔性流水车间可行解Sch
Output:一个柔性流水车间可行解Sch
1. for k=1,2,⋮,m
2.ψ←加工工件数量大于1的机器集合
3. while ψ≠∅
4.φ1←ψ上第一台机器
6.α1←′上前round(num(′)/2)项
7.α2=′-{α1}
8. Sch1←修改Sch并行机φ1上工件加工顺序为{α1,α2}
9. Sch2←修改Sch并行机φ1上工件加工顺序为{α2,α1}
10. Sch=min{}
Makespan(Sch1,Sch2,Sch)
11.ψ=ψ-{φ1}
12. end
13. end
14. return Sch
以概率ppb对粒子群所有粒子执行NEH-Greedy搜索算法,增加粒子搜索空间,提高可行解质量。NEH-Greedy算法中对工件加工的所有m道工序循环操作,循环中对于工序i,判断所有并行机状态,产生新可行解,比较新可行解与原可行解,计算Makespan的复杂度为O(mn),因此该算法的时间复杂度为O(nm2)。
在柔性流水车间调度问题中,同一台机器上工件顺序将影响下一阶段工件的开始时间,从而影响问题的最大完成时间,而在目前对柔性流水车间调度问题的研究中几乎没有对同一台机器上工件顺序进行调优的算法,因此本文引入NEH-Greedy算法从新的优化角度扩大搜索范围。
3.5 SADA搜索算法
粒子群算法中的全体极值为当前粒子群最优解,为进一步扩大搜索范围,提高可行解质量,本文采用模拟退火扰动算法(simulated annealing disturb algorithm,SADA)。基本思想是在每轮迭代中,随机选择3种扰动方案之一产生新解ω′,计算新解ω′与原始解ω的目标值差值ΔE=Cω-Cω′,以概率min{1,exp(-ΔE/T)}更新新解,更新退火温度T=。TotalIte为MMPSO算法总迭代次数,ite为当前迭代次数。SADA搜索算法如下。
算法3 SADA搜索算法
Input:全体极值g,模拟退火温度T
Output:全体极值g
1. i=randi(3)
2. switch (i)
3. Case 1: (选择单点交换扰动)
4. k=randi(m)←随机选择一道加工工序
5. J1=rand(Ji|i=1,2,⋮,n)
6. J2=rand(Ji|i=1,2,⋮,n)⋮←J1≠J2
7. g′←交换g中工件J1、J2在工序k的加工机器
8. Case 2:(选择插入扰动)
9. J1=rand(Ji|i=1,2,⋮,n)
10. J2=rand(Ji|i=1,2,⋮,n)←J1≠J2
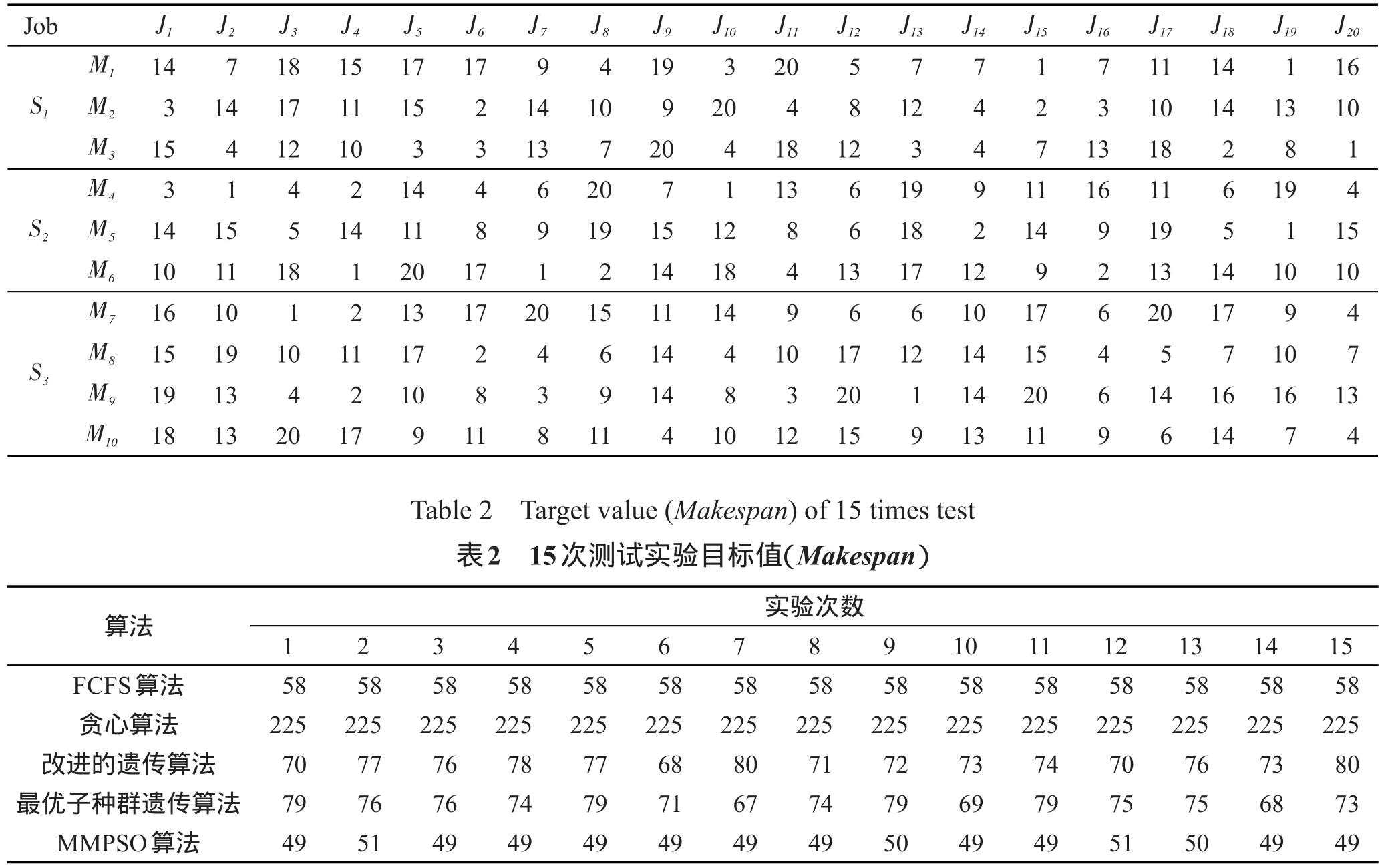
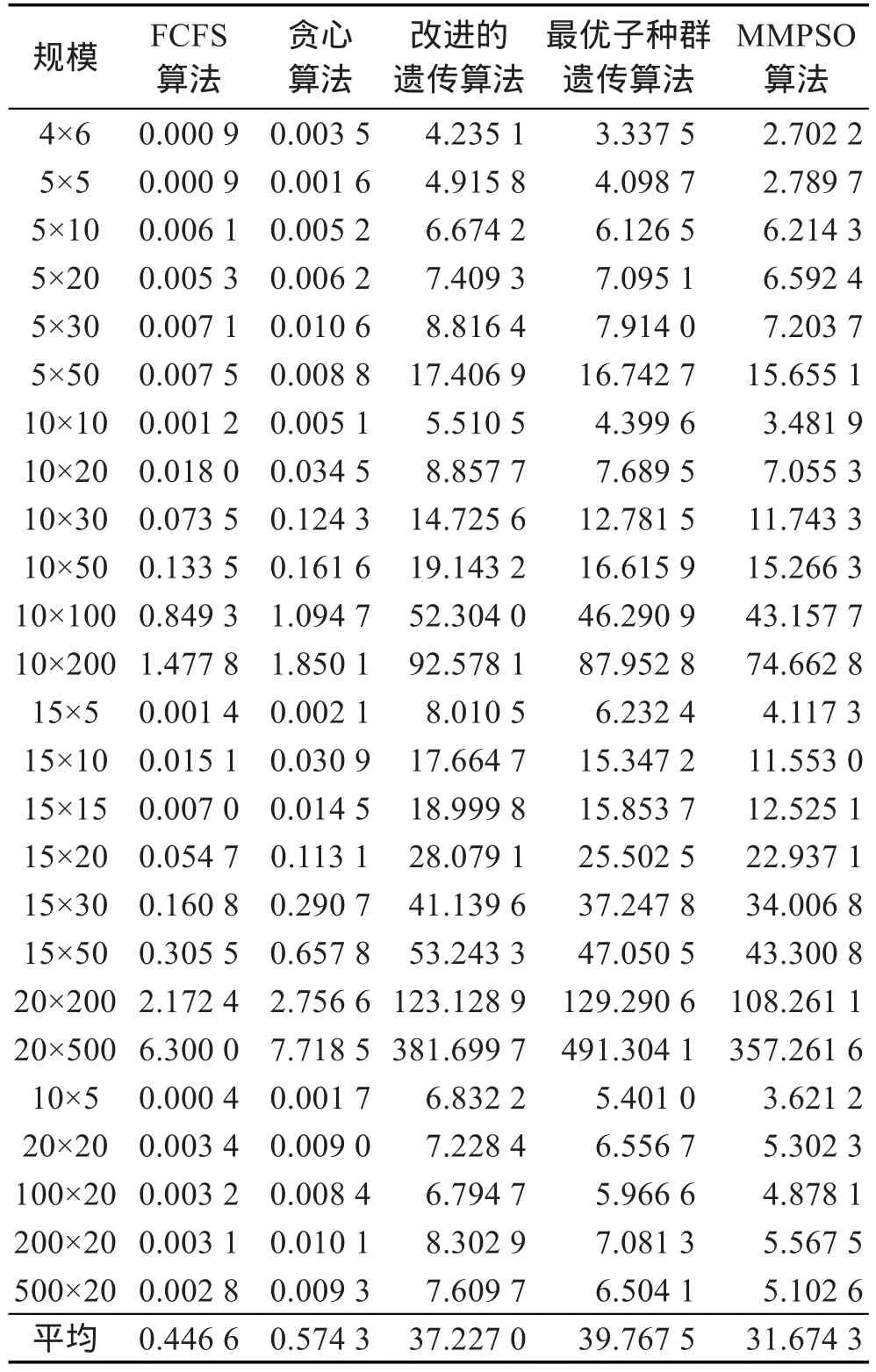
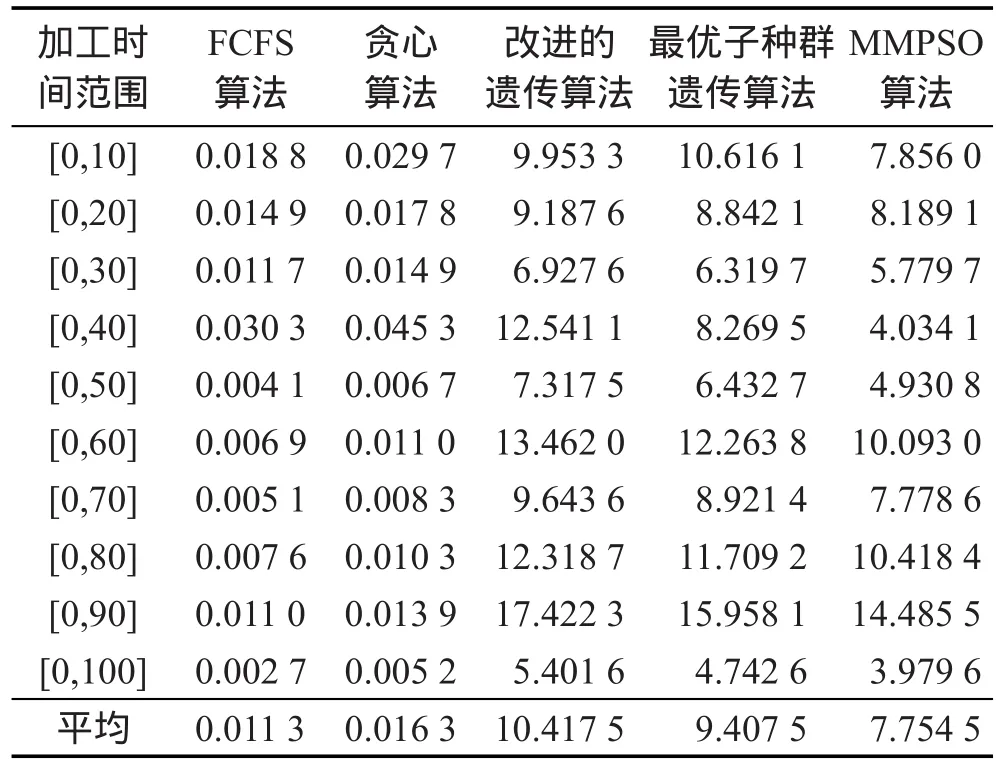
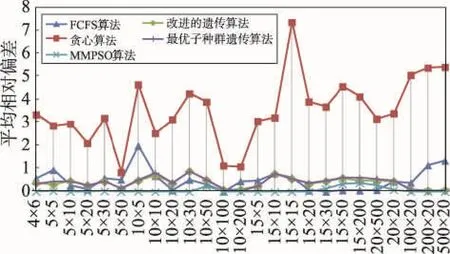
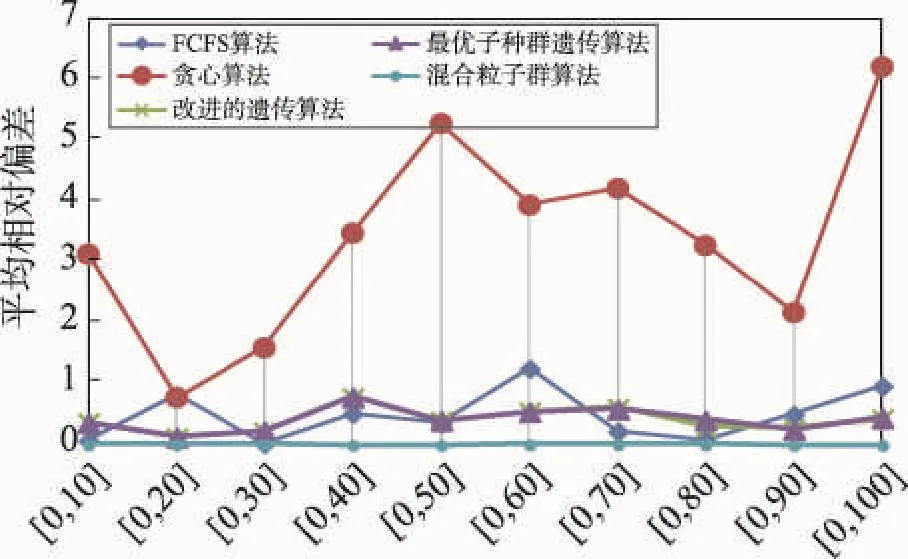
11. if J1 12. g′←将g中工件J2信息插入到J1之前(即第j列数据插入到第i列前) 13. else 14. g′←将g中工件J1信息插入到J2之前 15. end 16. Case 3:(选择子排序交换扰动) 17. J1=rand() Ji|i=1,2,⋮,n 18. J2=rand(Ji|i=1,2,⋮,n)⋮←J1≠J2 19. g′←交换g中工件J1和J2的调度信息(即交换调度信息矩阵中第j列和第i列数据) 20. end 21.ΔE=Cg-Cg′←原始解g与扰动新解g′的Makespan差 22. p=min{1,exp(-ΔE/T)} 23. if rand(1) 24. g=g′ 25. end 27. return g SADA搜索算法中,单点交换扰动与子排序交换扰动均为交换操作,时间复杂度为常数级,即O(1);选择插入扰动中,插入操作的复杂度为O(n),因此该算法复杂度为O(n)。 SADA算法随机选择单点交换扰动、插入扰动、子排序交换扰动3种策略之一搜索全体极值邻域,比单一搜索策略较大程度地扩大了搜索范围。 SADA算法的3种扰动算法以粒子间排序信息为搜索对象,NEH-Greedy算法以同一台机器上的工件加工顺序为优化搜索目标,两种算法从不同角度扩大粒子群搜索范围,加快收敛速度。 3.6随机扰动算法 若最优粒子在一定迭代次数内未更新,表明粒子可能陷入局部最优,则对最优粒子以概率pRPA进行随机扰动操作,避免局部最优,改变粒子停滞状态。随机扰动算法(random perturbation algorithm,RPA)如下。 算法4随机扰动算法 Input:全体极值g Output:全体极值g 1. if rand(1)≤pRPA 2. Jα=rand(Ji|i=1,2,⋮,n) 3.在并行机编号限定范围内对工件Jα每道工序加工机器(即调度矩阵第α列数据)进行随机重置 4. end 5. return g 3.7更新惯性权重 惯性权重更新公式如下: 其中,ωstart为惯性权重初始值;ωend为算法达到最大迭代次数的惯性权重取值;TotalIte为种群迭代次数;ite为当前迭代次数。 本文以递减凹函数ω作为种群更新的惯性权重。在算法初期以个体极值为主要参考进行更新操作,以局部寻优为主,使算法较快进入局部最优;算法后期则以全体极值为参考,以RPA算法帮助粒子跳出局部最优,增强全局搜索能力,保证了全局搜索和局部搜索之间的平衡。 基于以上思想及算法,MMPSO算法流程如图2所示。 Fig.2 Flow chart of MMPSO图2 MMPSO算法流程图 经以上分析,MMPSO算法的时间复杂度为O(TotalIte×nm2)。 为验证本文MMPSO算法的正确性与有效性,将MMPSO算法与FCFS算法、贪心算法[5]、改进的遗传算法[6]和最优子种群遗传算法[13]进行仿真实验和比较。各个算法在Matlab 2014a上编程实现,算法运行在CPU为Intel®CoreTMi5-3470 3.20 GHz,内存为8 GB 的PC上。经过实验,MMPSO算法中惯性权重取值为ωstart=0.94,ωend=0.4,模拟退火初始温度T=0.64,其他参数设置为种群规模PS=30,迭代次数TotalIte=50。 由于目前针对柔性流水车间调度问题没有标准的测试实例集,本文采用随机策略产生测试实例集。实例中工件加工时间为{1,2,⋮,20}上的随机数。例如:根据随机策略产生问题规模(总并行机数×工件数)为10×20的一个柔性流水车间调度问题实例的数据如表1所示。 以表1为实例,对FCFS算法、贪心算法、改进的遗传算法、最优子种群遗传算法和MMPSO算法分别进行两项实验:算法所得可行解质量及算法收敛速度。 Table 1 An instance of flexible flow shop scheduling problem表1 一个柔性流水车间调度问题实例 运用以上5种算法对表1所示的实例分别独立运行15次,各算法目标值如表2所示。 由表2可知,FCFS算法和贪心算法中不存在解的更新机制,因此实验所得目标函数值没有变化,可行解质量有待提高;而改进的遗传算法、最优子种群遗传算法能不断更新解的质量,但在多次测试中所得可行解并不唯一,可行解质量比FCFS算法和贪心算法有所提高;本文提出的MMPSO算法在15次实验中12次取得较优解Makespan=49,说明本文算法有效提高了可行解质量。 针对表1所示的实例,对比混合粒子群算法、最优子种群遗传算法和改进的遗传算法收敛速度,结果如图3所示。 Table 3 Average relative deviation of solution computing by algorithms (Group A)表3 算法所得解平均相对偏差(A组) Fig.3 Objective function values change graph图3 算法目标函数值变化曲线图 由图3可知,MMPSO算法在种群初始阶段便能得到优于最优子种群算法和改进的遗传算法的可行解,且随着迭代次数增加收敛速度最快,最早得到优化解,优化解质量最高。而最优子种群遗传算法和改进的遗传算法收敛速度较慢,且最优解质量差于MMPSO算法。这是由于MMPSO算法在初始化阶段加入对初始粒子的优化算法BMEA算法,可找到较优的可行解,在算法迭代过程中增加NEH-Greedy算法和SADA搜索算法,有效扩大了搜索空间,使得算法收敛速度较快,且引入对当前最优解的RPA扰动,防止算法陷入局部最优,最终使得问题可行解质量有了进一步提高。 单一实例测试具有偶然性,且本研究领域目前没有统一的测试实例集,因此为验证本文算法的适用性,采用随机策略产生测试实例集。测试实例集分为A、B两组不同参数实例。 A组25组不同规模(机器总数×工件数)实例,问题规模分别为4×6、5×5、5×10、5×20、5×30、5×50、10×10、10×20、10×30、10×50、10×100、10×200、15×5、15×10、15×15、15×20、15×30、15×50、20×200、20×500、10×5、20×20、100×20、200×20、500×20。工件在每台机器上的加工时间为[1,20]上的随机整数,保证工件在各并行机上的加工时间不完全相同。 B组测试实例问题规模为10×20。10组不同工件加工时间分别在[1,10]、[1,20]、[1,30]、[1,40]、[1, 50]、[1,60]、[1,70]、[1,80]、[1,90]、[1,100]上随机产生。 对于每一组实例分别运行FCFS算法、贪心算法、改进的遗传算法、最优子种群遗传算法、MMPSO算法各15次,计算相对偏差及运行时间以评价算法质量。平均相对偏差计算公式为: 式中,Li为算法i(i∈S)的输出结果,S={FCFS算法,贪心算法,改进的遗传算法,最优子种群遗传算法,MMPSO算法};L*=min(Li)。比较各算法平均相对偏差如表3、表4所示,运行时间如表5、表6所示。 Table 4 Average relative deviation of solution computing by algorithms (Group B)表4 算法所得解平均相对偏差(B组) Table 5 Running time of algorithms (Group A)表5 算法运行时间(A组) s Table 6 Running time of algorithms (Group B)表6 算法运行时间(B组) s 由表3可知,对于以上5种对比算法的平均相对偏差而言,在不同问题规模下,实例中工件顺序具有随机性,且FCFS算法较大依赖于待加工工件的初始顺序,因此随着问题规模的变化FCFS算法的相对偏差表现较差,个别实例测试中表现较好,优化效果波动明显;贪心算法相对偏差最大,优化效果最差;改进的遗传算法与最优子种群遗传算法有近似的优化性能,相对偏差表现相近,区别不明显,但明显优于FCFS算法和贪心算法;MMPSO算法相对偏差最小,在不同规模的测试实例下均能得到较好的可行解,具有较好的有效性。为了更清晰地比较和评价各算法的优劣,给出了A组测试实例集的平均相对偏差对比图,如图4所示。 Fig.4 Average relative deviation comparison (Group A)图4 平均相对偏差对比图(A组) 在机器数与工件数的数量差距较大时,FCFS算法与贪心算法的平均相对偏差增大,算法表现不稳定;而智能优化算法此类情况下表现优秀,其中MMPSO算法表现最佳,平均相对偏差最小,说明MMPSO算法能较好解决不同规模比例的柔性流水车间调度问题。 表4中,工件加工时间的随机取值范围变化,贪心算法在少数实例下能得到较好的解,相对偏差较小,但大多数情况平均相对偏差较大,且优化效果不稳定;FCFS算法平均相对偏差表现一般,但在加工时间有较大差值时,优化效果出现较大偏差;改进的遗传算法与最优子种群遗传算法在加工时间[0,20]区间内表现最好,相对偏差最小,在所有实例集测试中波动幅度不大;MMPSO算法平均相对偏差最小且几乎没有较大波动,同样能较好地解决不同加工时间范围内的柔性流水车间调度问题,优于其他算法。B组测试实例集的平均相对偏差对比图如图5所示。 Fig.5 Average relative deviation comparison (Group B)图5 平均相对偏差对比图(B组) 对比各算法的时间效率,如表5、表6所示,虽然FCFS算法和贪心算法速度较快,但优化效果差,给实际应用带来较大的损失;而基于群体的智能优化算法虽然时间消耗较大,但在可接受的时间范围内得到较好的可行解,在实际应用过程中能大大降低生产成本,提高利润。比较改进的遗传算法、最优子种群遗传算法和MMPSO算法均属于智能优化算法,其中MMPSO算法运行时间最短,且对比表4、表5,MMPSO算法相对偏差最小,可行解最优。 综上所述,本文MMPSO算法对于柔性流水车间调度问题的求解是非常有效的,而且MMPSO算法性能明显优于参与比较的其他算法。 针对柔性流水车间调度问题的特点,分析现有粒子群算法和模拟退火算法的优势及不足,本文提出了MMPSO算法。以粒子群算法为基础,MMPSO算法初期在解空间内随机产生粒子群信息,通过BMEA算法对随机选择的初始粒子进行优化操作,在保证种群多样性的基础上避免瓶颈机器出现,提高了初始种群质量。随后按照合法性更新策略更新粒子信息。在算法迭代过程中,为扩大粒子搜索范围,本文提出了两种搜索算法:(1)在结合NEH算法和贪心算法基础上提出NEH-Greedy搜索算法,对粒子群个体极值执行NEH-Greedy算法操作,提高可行解质量,扩大算法搜索范围;(2)对粒子全体极值执行SADA搜索算法,进一步扩大粒子搜索范围。同时加入RPA扰动操作,使处于静止状态的全体极值跳出局部最优状态。仿真实验证明了MMPSO算法具有较强的有效性和适用性。 References: [1] Hong Wang. Flexible flow shop scheduling optimum heuristics and artificial intelligence solutions[J]. Expert Systems, 2005, 22(2): 78-85. [2] Jungwattanakit J, Reodecha M, Chaovalitwongse P, et al. Algorithms for flexible flow shop problems with unrelated parallel machines, setup times, and dual criteria[J]. International Journal of Advanced Manufacturing Technology, 2008, 37(3/4): 354-370. [3] Hoogeveen J A, Lenstra J K, Veltman B. Preemptive scheduling in a two-stage multiprocessor flow shop is NP-hard[J]. European Journal of Operational Research, 1996, 89(1): 172-175. [4] Linn R. Hybrid flow shop scheduling: a survey[J]. Computers & Industrial Engineering, 1999, 37(1/2): 57-61. [5] Li Xiaofeng, Zhao Hai, Du Hongjun, et al. Greedy algorithm solution of flexible flow shop scheduling problem[J]. Jilin University Journal, 2009, 27(6): 585-589. [6] Wang Xudong, Dai Qingyun. Scheduling for flexible flowshop problem based on an improved genetic algorithm[C]// Proceedings of the 2014 IEEE International Conference on Consumer Electronics-China. Piscataway, USA: IEEE, 2014: 1-3. [7] Song Ye, Yang Genke. Real time scheduling using branchbound algorithm and artificial neural network[J]. ComputerSimulation, 2008, 25(12): 321-324. [8] Xuan Hua, Tang Lixin. Lagrangian relaxation algorithm for real-time hybrid flowshop scheduling with no-wait in process[J]. Control and Decision, 2006, 21(4): 376-380. [9] Sun Ying, Chi Hong, Jia Chuanliang. Nonlinear mixed-integer programming model for emergency resource dispatching with multi-path[J]. Operations Research and Management Science, 2007, 16(5): 5-8. [10] Liu Bo, Wang Ling, Jin Yihui. An effective PSO-based memetic algorithm for flow shop scheduling[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2007, 27(1): 18-27. [11] Akhshabi M, Tavakkoli-Moghaddam R, Rahnamay-Roodposhti F. A hybrid particle swarm optimization algorithm for a no-wait flow shop scheduling problem with the total flow time[J]. International Journal of Advanced Manufacturing Technology, 2014, 70(5): 1181-1188. [12] Zhang Changsheng, Sun Jigui, Zhu Xingjun, et al. An improved particle swarm optimization algorithm for flow shop scheduling problem[J]. Information Processing Letters, 2008, 108(4): 204-209. [13] Wang Jinpeng, Zhu Hongjun, Zhou Jun. Optimal sub-population genetic algorithm for flexible flow shop scheduling problem[J]. Application Research of Computers, 2012, 29 (2): 442-444. [14] Hertz A. Finding a feasible course schedule using tabu search[J]. Discrete Applied Math, 1992, 35(3): 255-270. [15] van Laarhoven P J M, Aarts E H L, Lenstra J K. Job shop scheduling by simulated annealing[J]. Operation Research, 1992, 40(1): 113-125. [16] Zandieh M, Fatemi Ghomi S M T, Moattar Husseini S M. An immune algorithm approach to hybrid flow shops scheduling with sequence-dependent setup times[J]. Applied Mathematics and Computation, 2006, 180(1): 111-127. [17] Mastrolilli M, Gambaroella L M. Effective neighborhood functions for the flexible job shop problem[J]. Journal of Scheduling, 2000, 3(1): 3-20. [18] Shen Bin, Zhou Yingjun, Wang Jiahai. Flow job shop scheduling based on self-adaptive genetic algorithm[J]. Computer Engineering, 2010, 36(14): 201-203. 附中文参考文献: [5]李晓峰,赵海,杜洪军,等.柔性流水作业排序问题的贪心算法求解[J].吉林大学学报, 2009, 27(6): 585-589. [7]宋晔,杨根科.基于分支定界和神经网络的实时调度策略[J].计算机仿真, 2008, 25(12): 321-324. [8]轩华,唐立新.实时无等待HFS调度的一种拉格朗日松弛算法[J].控制与决策, 2006, 21(4): 376-380. [9]孙颖,池宏,贾传亮.多路径下应急资源调度的非线性混合整数规划模型[J].运筹与管理, 2007, 16(5): 5-8. [13]王金鹏,朱洪俊,周俊.最优子种群遗传算法求解柔性流水车间调度问题[J].计算机应用研究, 2012, 29(2): 442-444. [18]沈斌,周莹君,王家海.基于自适应遗传算法的流水车间作业调度[J].计算机工程, 2010, 36(14): 201-203. ZHANG Haiyue was born 1990. She is an M.S. candidate at Guizhou university. Her research interest is algorithms design and analysis.张海月(1990—),女,河北唐山人,贵州大学硕士研究生,主要研究领域为算法设计与分析。 QIN Yongbin was born in 1980. He is an associate professor and M.S. supervisor at Guizhou university, and the member of CCF. His research interests include computability and computational complexity, intelligent computing and trusted computing.秦永彬(1980—),男,山东人,贵州大学副教授、硕士生导师,CCF会员,主要研究领域为可计算性和计算复杂性,智能计算,可信计算。 XU Daoyun was born in 1959. He is a professor and Ph.D. supervisor at Guizhou University, and the senior member of CCF. His research interests include computability and computational complexity, algorithms design and analysis.许道云(1959—),男,贵州安顺人,贵州大学教授、博士生导师,CCF高级会员,主要研究领域为可计算性和计算复杂性,算法设计与分析。 Multi-Search Mechanism Particle Swarm Optimization Algorithm for Solving FFS Problemƽ ZHANG Haiyue, QIN Yongbin, XU Daoyun+ ZHANG Haiyue, QIN Yongbin, XU Daoyun. Multi-search mechanism particle swarm optimization algorithm for solving FFS problem. Journal of Frontiers of Computer Science and Technology, 2016, 10(3):433-444. Abstract:For the flexible flow shop scheduling (FFS) problem, this paper proposes a multi-search mechanism particle swarm optimization algorithm (MMPSO) in order to obtain a better optimal solution. Based on the analysis of the characteristics of flexible flow shop scheduling problem, this paper designs a particle information encoding scheme for the problem, then proposes the bottleneck machine elimination algorithm to improve the quality of initial population, while using NEH-Greedy search algorithm in the individual extremum search and SADA (simulated annealing disturb algorithm) search algorithm in all extremum search, which are both used to widen the search scope, improve the quality of feasible solutions and speed up the convergence process, in the iterative search RPA (random perturbation algorithm) operations are used to avoid plunging local optimum for all extremum. The experimental results show that the proposed algorithm can obtain a good optimal solution of this flexible flow shop scheduling problem by a faster convergence rate. doi:10.3778/j.issn.1673-9418.1511041 文献标志码:A 中图分类号:TP391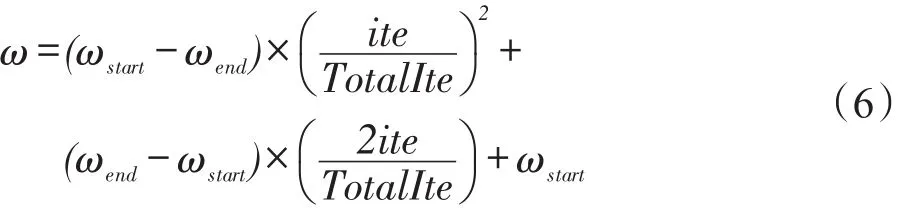
4 实验仿真
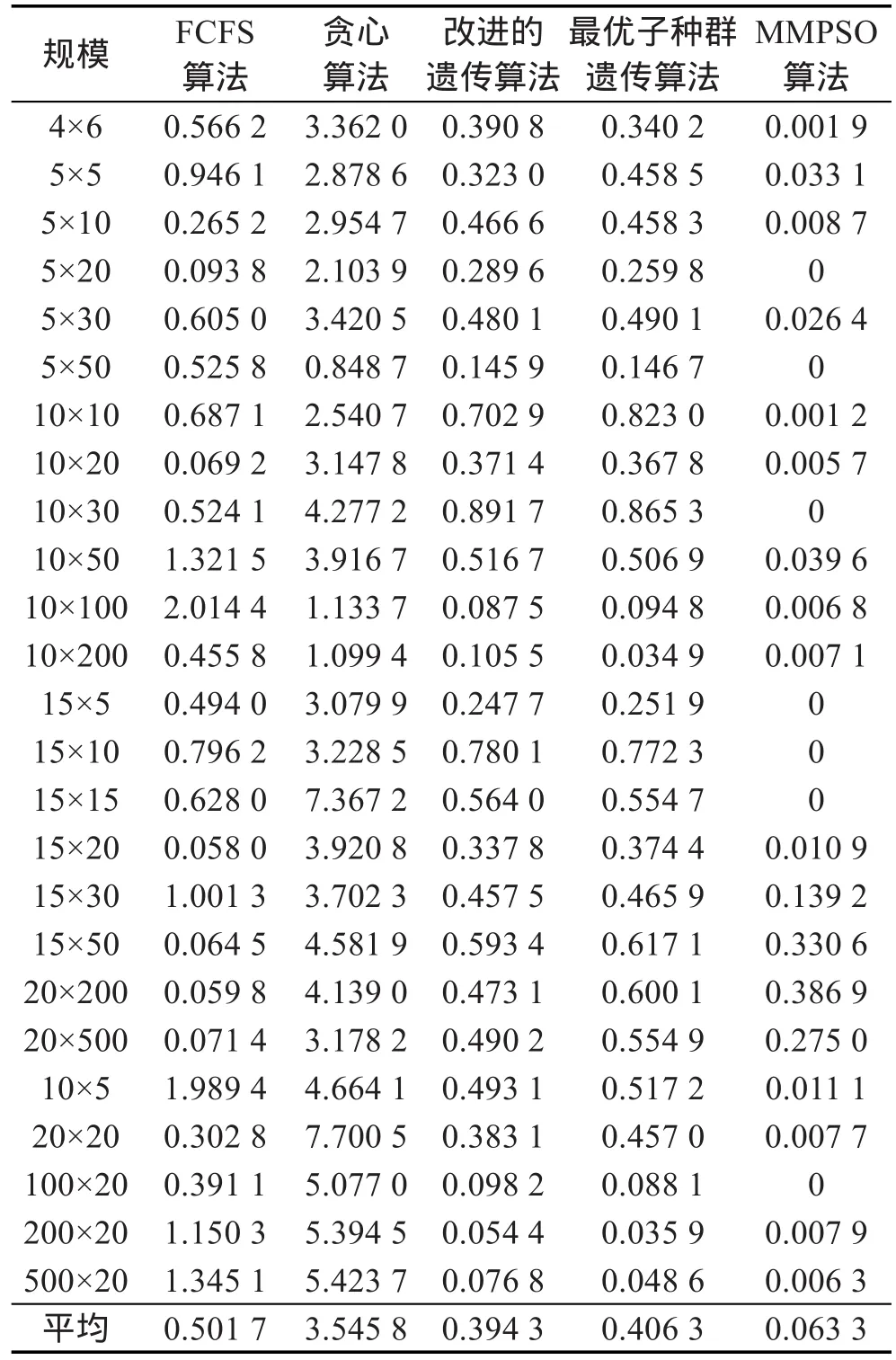
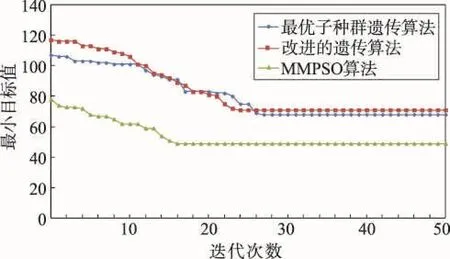
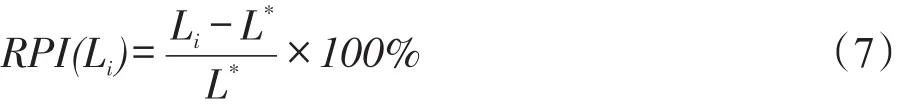
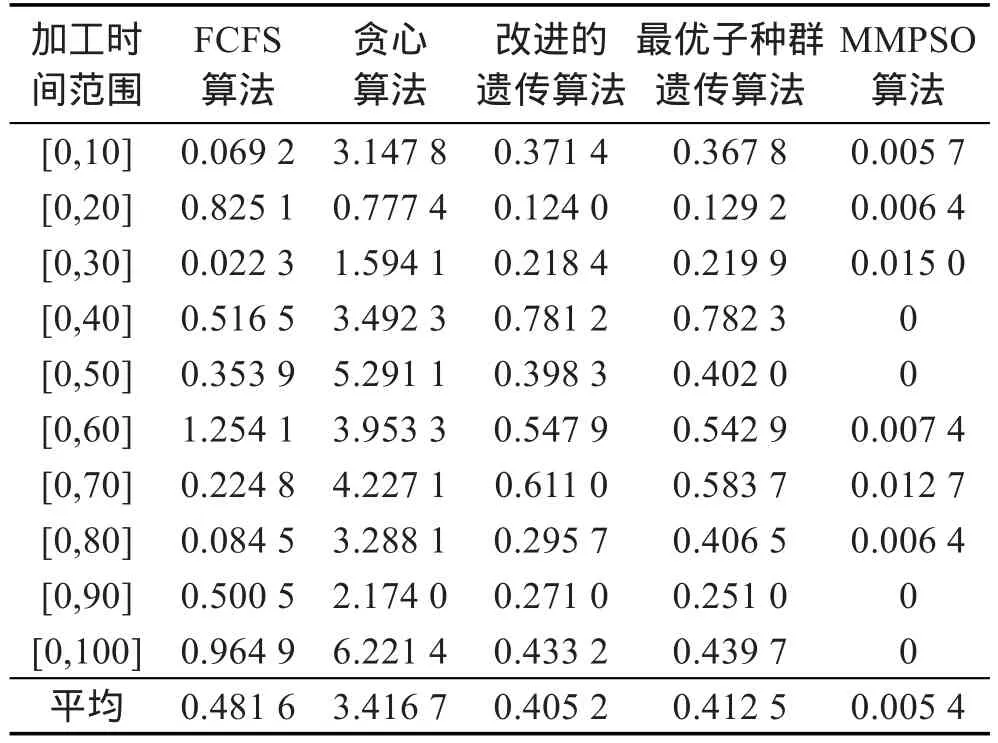
5 结束语



College of Computer Science and Technology, Guizhou University, Guiyang 550025, China
+ Corresponding author: E-mail: dyxu@gzu.edu.cn

