利用边信息的混合距离学习算法*
郭瑛洁,王士同
江南大学数字媒体学院,江苏无锡214122
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(03)-0414-11
利用边信息的混合距离学习算法*
郭瑛洁+,王士同
江南大学数字媒体学院,江苏无锡214122
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(03)-0414-11
E-mail: fcst@vip.163.com
http://www.ceaj.org
Tel: +86-10-89056056
* The National Natural Science Foundation of China under Grant No. 61272210 (国家自然科学基金). Received 2015-05,Accepted 2015-08.
CNKI网络优先出版: 2015-08-28, http://www.cnki.net/kcms/detail/11.5602.TP.20150828.1604.010.html
摘要:使用边信息进行距离学习的方法在许多数据挖掘应用中占有重要位置,而传统的距离学习算法通常使用马氏距离形式的距离函数从而具有一定的局限性。提出了一种基于混合距离进行距离学习的方法,数据集的未知距离度量被表示为若干候选距离的线性组合,利用数据的边信息学习得到各距离所占权值从而得到新的距离函数,并将该距离函数应用于聚类算法以验证其有效性。通过与其他已有的距离学习方法进行对比,基于UCI(University of California,Irvine)数据集的实验结果证明了该算法具有明显的优势。
关键词:距离学习;混合距离;距离函数;边信息
1 引言
合适的距离度量在数据挖掘和机器学习领域占有重要的位置,是科学和工程领域中的基础问题,对许多应用都有着重要的影响,比如信息检索、基于内容的图像视频检索、手写识别等。
在众多的数据挖掘应用中,使用最多的距离度量是欧氏距离。但是采用欧氏距离的方法通常先假设所有的变量都是不相关的,并且数据所有维度的方差为1,所有变量的协方差为0[1]。然而这些条件在实际应用中很难实现。此外,欧氏距离仅适用于特征空间中超球结构的数据集,对超立方体结构、超椭球结构的数据集效果不太理想[2]。因此,在许多实际应用中,欧氏距离并不是最理想的选择。
针对这些问题,近年来在数据挖掘和机器学习领域已经提出了多种方法来学习数据集中的未知距离。研究者们尝试自动地从数据集中学习新的距离函数来替代欧式距离。
在众多的距离学习方法中,有一类方法利用数据的边信息来进行距离学习,而其中边信息通常以成对约束的形式来表示[3]。与用来训练分类模型的类标不同的是,由成对约束表示的边信息在实际应用中更容易获得,且付出的代价更少。比如,对于多媒体应用,边信息可以从用户的相关反馈日志中获得。
在之前的研究中,人们提出了许多利用边信息进行距离学习的方法,比如将距离学习转化为凸优化问题的方法[4]、相关成分分析法[5]、区分成分分析法[6]等。然而这些方法大多数都将目标距离函数假设在马氏距离定义的框架下,即给定两个点x、y,它们之间的距离公式为d(x,y)=(x-y)TA(x-y)。其中,矩阵A为要学习的距离矩阵。如果A取单位矩阵I,则以上公式表示欧式距离。因此,本质上来说,针对马氏距离学习得到的新距离是欧式距离的线性变换。这些距离在数据集结构和特点未知的情况下,不一定能很好地表示数据点之间的远近。
针对这些问题,本文提出了一种新的距离学习方法。与传统的距离学习方法不同的是,本文方法没有局限于学习马氏距离形式的距离度量,而是将适合于数据集的未知距离表示为若干候选距离的线性组合,其中未知距离的权值将通过数据的边信息学习得到。在候选距离的选择上采用了一些非线性的距离度量进行组合,以提升聚类效果。
本文组织结构如下:第2章提出了一种距离学习的新方法——利用边信息学习基于线性组合的混合距离,并给出了求解距离分量对应权值的公式与方法;第3章将学习得到的距离函数应用于聚类算法中;第4章给出了算法的对比实验,通过实验说明本文方法的有效性;第5章给出结论。
2 混合距离学习
2.1基于线性组合的混合距离
由于不同数据集的结构和特点不同,为了合理地计算不同数据集之间的距离,在聚类过程或距离函数中引入权重已经成为一种常用的方法。通过学习得到的权重可以强化重要的特征或距离,削减冗余的信息。比如,通过特征加权的方式来优化聚类算法[7],在距离函数中加入特征权重的方法[8],组合距离的方法[2]等。
本文通过以下线性组合来表示数据集中的位置距离度量:
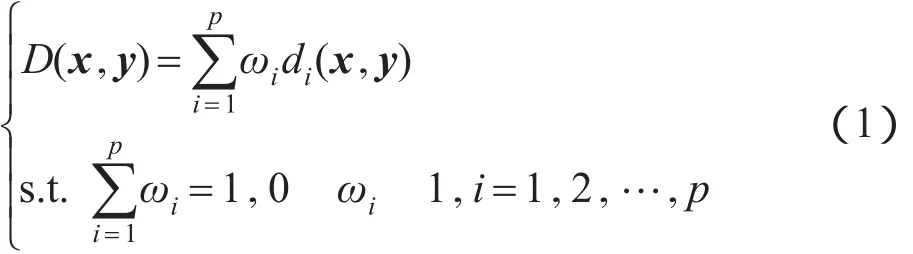
其中,D(x,y)表示数据点x到数据点y之间的距离,由p个距离分量组成;di(x,y)是其第i个距离分量;ωi是第i个距离分量对应的权值。
距离度量D(x,y)本质上是一个函数,给出了两个模式之间标量距离的大小。对于任意的向量x、y、z,距离度量函数应满足如下性质[9]:
(1)非负性,D(x,y)≥0;
(2)自反性,D(x,y)=0当且仅当x=y;
(3)对称性,D(x,y)=D(y,x);
(4)三角不等式,D(x,y)≤D(x,z)+D(z,y)。
定理如果di(x,y)是一个距离,则其线性组合D(x,y)=ωidi(x,y)也是一个距离。
证明条件(1)、条件(2)、条件(3)易证。以下将证明线性组合距离满足条件(4):
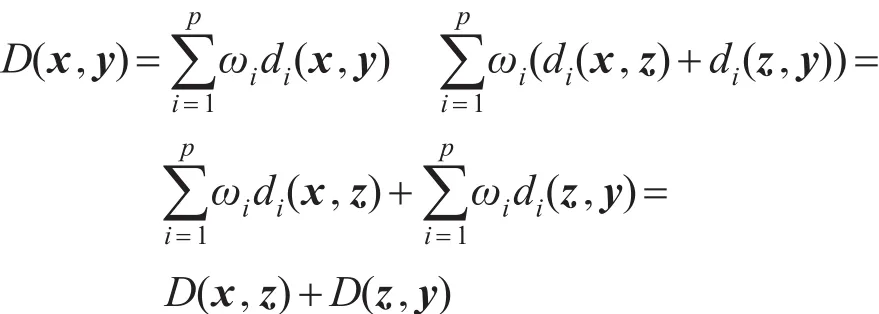
即D(x,y)≤D(x,z)+D(z,y)。因此,线性组合D(x,y)是一个距离。
距离分量越多越能够拟合出好的距离函数,而越多的距离分量会导致距离学习的计算量增加。为了更好地拟合出合适的距离函数,在考虑学习效率的前提下,本文预设10个经典的距离度量进行组合以学习得到一个新的距离函数。这10个距离度量如下:
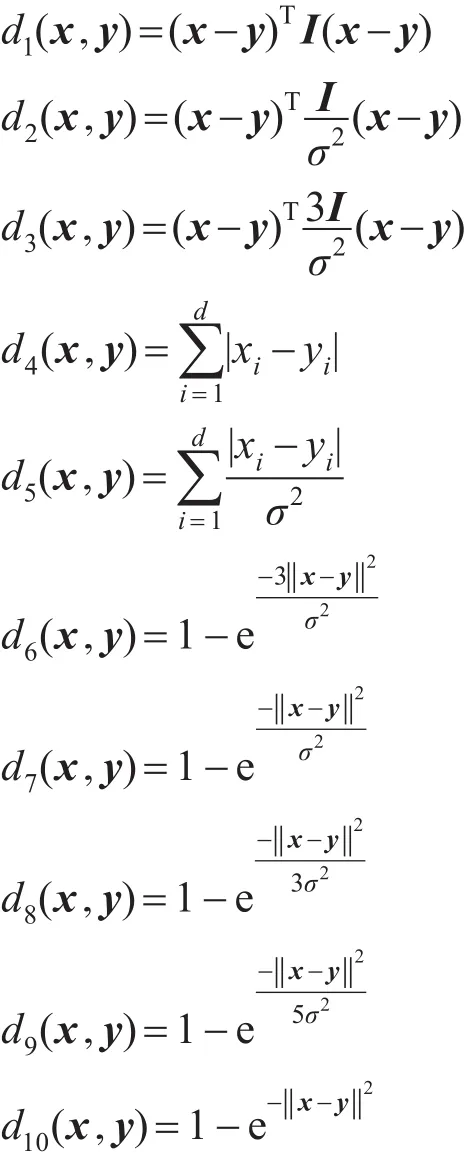
对于距离分量的选取,出于以下考虑:首先,欧式距离d1(x,y)并没有考虑到数据集各个维度的特征,因此使用若干含有方差的距离分量以保留数据各特征分量上的特征,如距离分量d2(x,y)、d3(x,y)。其次,这些距离均为基于欧式的距离度量,对其进行线性组合后,得到的距离函数仍为马氏距离,因此根据Wu等人提出的新距离[10],本文给出了距离分量d6(x,y)~d10(x,y)。这些距离均为非线性的距离度量,如此便可以组成非线性的距离函数。曼哈顿距离可以视为数据点之间在各个维度的平均差,它在一定程度上使得离群点的影响减弱,因此本文加入曼哈顿距离d4(x,y)、d5(x,y)以增加距离分量的多样性。
2.2混合距离学习
在距离学习的过程中,借鉴文献[1]的思想,利用最大间隔的框架优化以下目标函数:
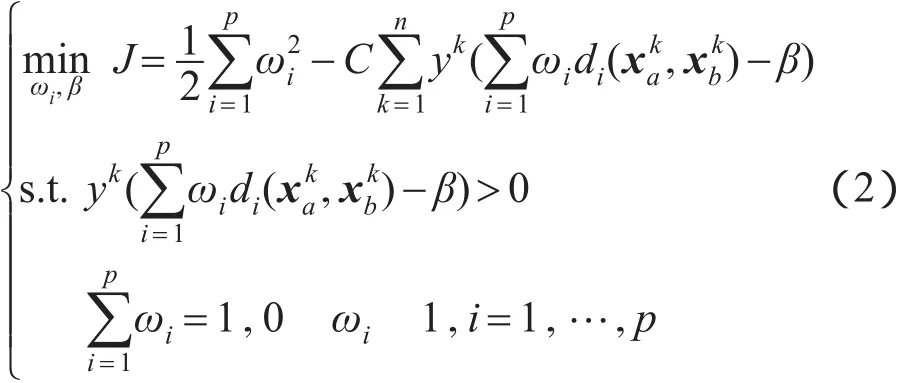
由上述公式可以看到,距离学习问题被转化为带有约束条件的优化问题,可以使用拉格朗日乘子法对式(2)所表示的优化问题进行求解,所得到的拉格朗日函数如下:
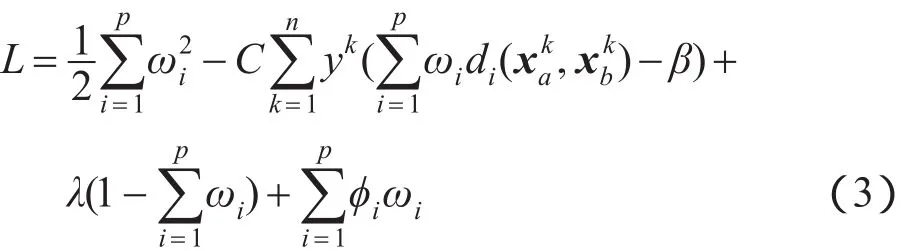
其中,λ和ϕi为拉格朗日乘子。则式(3)的最优化(Karush-Kuhn-Tucker,KKT)条件为:

显然由方程组(4)无法求得ωi,因此本文先暂时舍弃ωi非负的条件,构建如下拉格朗日函数:
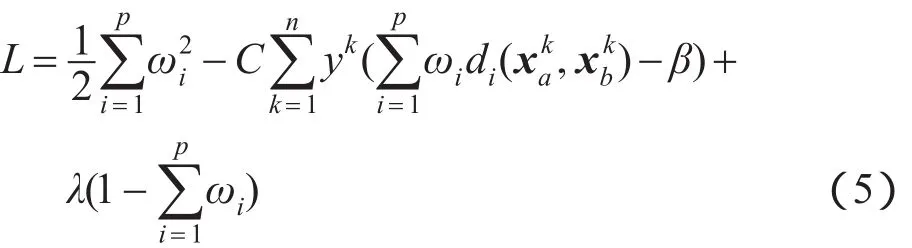
对上述拉格朗日函数进行求解得到:

求解方程组(6)分别得到如下等式:
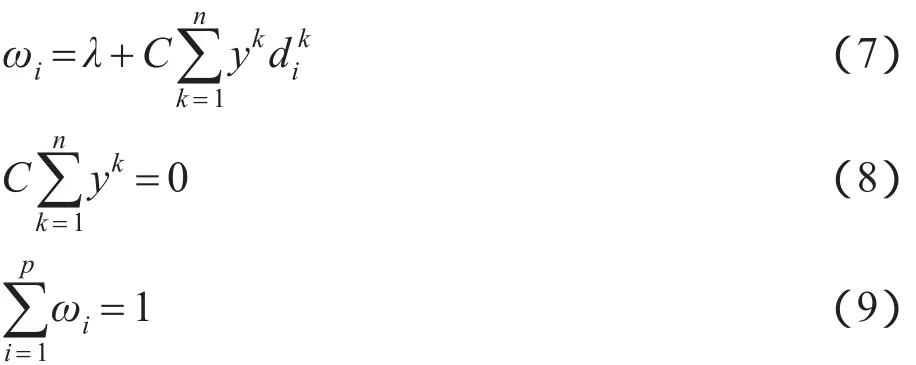
将式(7)代入式(9)得到:

再将式(10)代入式(7)得到:
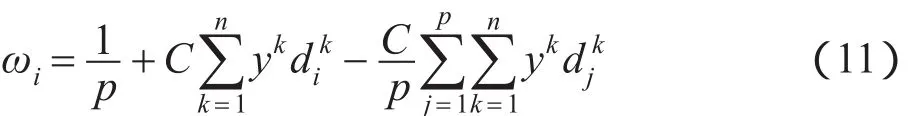
由式(11)可以明显看到,即使在成功的优化过程中ωi也可能会出现负值。由前文可知,在考虑ωi非负条件的情况下,无法通过构建拉格朗日函数求解。因此,受加权中心模糊聚类算法[11]的启发,将ωi的解改写为:其中,p+表示所有使得ωi取正值的i的集合;p-表示无法使ωi取正值的i的集合。本文使用|p+|和|p-|来分别表示集合p+和p-的大小。
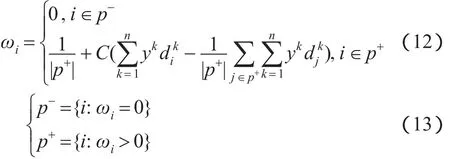
求解集合p+和p-的细节将在算法1中给出。

对于阈值β,使用梯度下降的方法进行求解,通过对式(2)进行求导,得到β的梯度如下:为了满足式(2)中的约束条件ykωidi()-β)>0,参考式(12)的表示方式,将符合约束条件的yk使用集合n+={ykÎD: ykωidi(,)-β) >0}表示,重新定义了β的梯度公式:

其中,|n+|表示集合n+的大小。
因此,根据梯度下降,新的解β′可被表示如下:
β′=β-γÑβJ(16)其中,γ表示梯度下降的学习速率,本文参考Pegasos Algorithm[12]中的方法,设置γ=1/t。
由于在求解β的过程中集合n+在不断改变,进一步修改式(12)为如下形式:
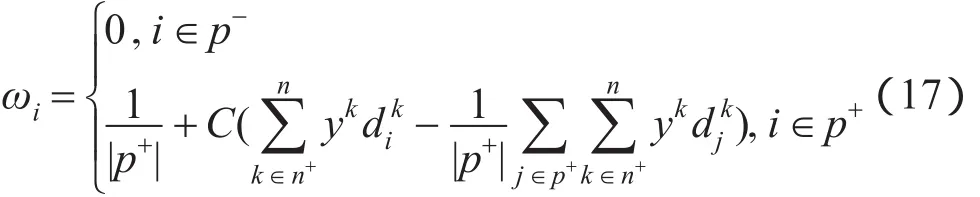
通过构建拉格朗日函数和梯度下降的方法对目标函数进行优化,完成了距离学习。下面将详细描述求解权值ωi的过程。
2.3算法描述
为了便于求解集合p+和p-,给出如下定义:
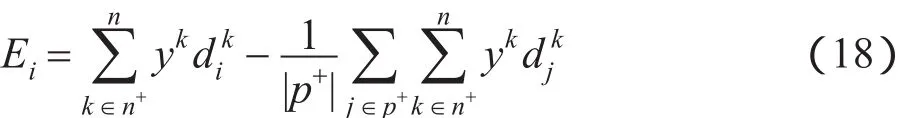
因而,式(12)被简化为:
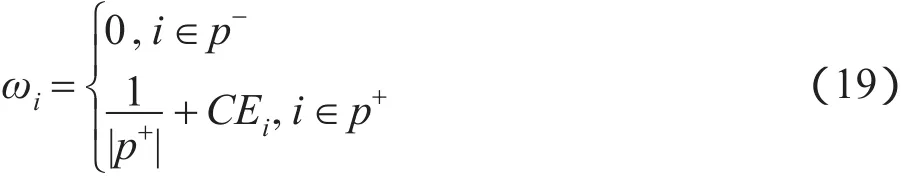
由式(19)显然可得,当Ei越大,则ωi为正值的几率越大。因此,求解集合p+和p-的算法总结如下。
算法1求解集合p+和p-
h-1
3.通过式(19)计算ωg并判断其是否大于0,其中g= argmini Îp+{Ei}。如果ωg>0则回到步骤2,否则设置p+=
h
下面将介绍求解权值ωi的算法。其中初始化ωi的方法比较简单,令==...=,根据式(2)中的约束条件有=1/p。而对于阈值β的初值设定,随机取一些点,在初始权值下取距离的最大值作为β的初值。
算法2学习距离函数
输入:数据矩阵XÎRd´N;成对约束(,yk),其中yk={+1,-1};惩罚因子C。
输出:距离权值ω;阈值β。
1.初始化:ω=ω(0), β=β(0)
2.计算距离矩阵:D(i,k)
3.设置迭代步数:t=1
4.循环,直至收敛,即ω的值不再变化
4.1更新学习率:γ=1/t, t=t+1
4.2更新训练集子集:
n+={ykÎD: ykωidi(,)-β) >0}
4.3计算梯度:ÑβJ=Cyk
4.4更新阈值:β′=β-γÑβJ
4.5更新集合p+和p-:算法1
4.6更新ω
通过以上算法即可求出参数ωi,进而得到新的距离函数。
由上述算法步骤可知,混合距离学习算法的时间复杂度为O(pT1n+pT2n),其中p为待组合的距离分量的个数,n为成对约束的个数,T1为算法1中收敛时的迭代次数,T2为算法2中收敛时的迭代次数。下面将介绍如何将距离函数应用在聚类算法中。
3 半监督聚类应用
一般来说,学习得到的距离函数可以被应用在任何需要距离度量的应用中。下面会将上文学习得到的距离函数应用在k-means聚类算法[13]中以检验距离函数。
3.1 P2C混合距离k-means聚类
一种简单的方法是直接将传统k-means算法中的欧氏距离用混合距离函数替换掉。因此,根据传统的k-means聚类算法,可以通过以下两步迭代实现聚类:
(1)使用混合距离函数将每一个点分配至距离它最近的类中,以形成k个类;
(2)更新每一个类的聚类中心。
对于每一个样本点xq,使用以下公式计算它与聚类中心wl之间的距离:
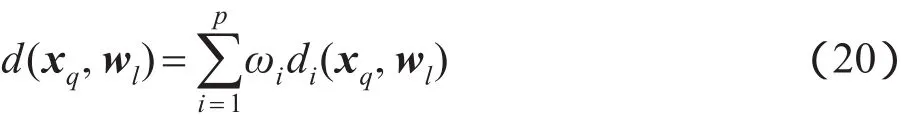
在上述聚类算法中,通过混合距离函数来计算样本点与聚类中心之间的距离,本文将该算法记为点到中心的混合距离k-means聚类算法(point-to-centroid hybrid distance k-means clustering method,HDK-P2C)。
3.2 P2P混合距离k-means聚类
与传统的k-means聚类算法相似,上述P2C混合距离聚类算法通过每个类的聚类中心来表示这个类,这也就暗中假设了数据集为球形结构,然而并不是所有的真实数据集都满足该结构。为了解决这种限制,受文献[1]启发,本文将距离函数应用在了另一种点到点的k-means聚类算法(point-to-point hybrid distance k-means clustering method,HDK-P2P),该算法并未假设数据集为球形结构。相似的想法在之前的聚类研究中也被提出过,比如凝聚层次聚类[14]和近邻传播聚类[15]。
与HDK-P2C方法不同的是,HDK-P2P聚类算法是通过计算样本点xq到类Wl中所有点的平均距离来衡量点xq到类Wl的亲近度。由于不需要在聚类过程中不断更新聚类中心,并且点到点的距离可以在聚类之前就计算完毕存储起来,HDK-P2P算法的效率要高于HDK-P2C算法。其具体实现步骤如下:
算法3点到点的混合距离k-means(HDK-P2P)
输入:数据矩阵XtestÎRd´Nt;权值向量ω;聚类数目k;聚类中心cen ÎRd´k。
输出:分类结果W={Wl}=1,Wl的聚类中心是wl。
1.设置t=0
2.循环,直至聚类中心不再改变
for q=1,2,...,Nt do
2.2计算聚类分配:
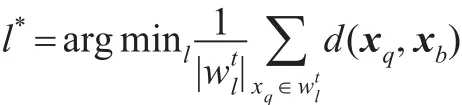
2.3更新聚类结果:
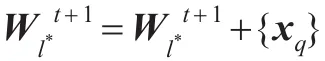
end for
t=t+1
4 实验
本文通过将距离函数应用在聚类算法中的表现来评价该距离函数。下面将本文提出的距离学习算法与其他距离学习算法进行对比,并均应用于kmeans聚类算法中进行验证。
4.1数据集与实验设置
实验数据集包含了12个来自UCI(University of California,Irvine)的真实数据集。其中7个为二类数据集,另外5个为多类数据集。各数据集的细节如表1。
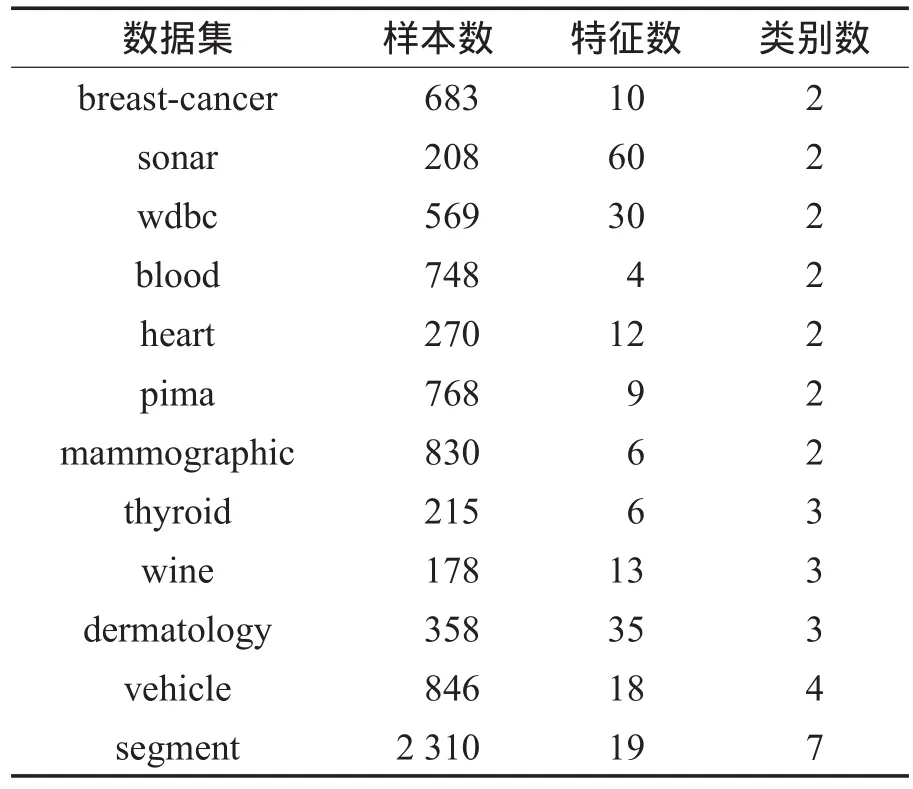
Table 1 List of datasets表1 实验中使用的数据集信息
本文选择这些数据集对算法进行测试是基于以下考虑。首先,这些数据集都拥有不同的性质,它们的类别数与特征数都不尽相同。再者,这些数据集作为基准数据集被广泛应用在机器学习的各项应用中。最后,它们都是真实的数据集,这些真实数据集可以验证本文算法在真实应用中是否可行。
在实验中,首先随机选取数据集中的一个子集(比如全部数据集的10%)来生成边信息,即根据这些样本点的原有类标来生成成对约束作为训练集。其中,拥有相同类标的样本点之间生成正约束对,拥有不同类标的样本点之间生成负约束对。生成全部的正约束对,再随机抽取相同数目的负约束对。
根据成对约束学习得到新的距离函数后,将其应用在全部的数据集中进行聚类。在聚类算法中,聚类数目依据数据集的类别数给定,初始聚类中心从数据集中随机抽取。为了保证可比性,本文所有的对比算法都将使用相同的初始聚类中心。重复每个聚类过程20次,实验结果取20次结果的均值。
4.2对比算法
本文将两种混合距离k-means聚类算法与已有的经典聚类算法和距离学习算法进行对比。包括以下算法:使用欧式距离的经典k-means聚类算法(k-means with Euclidian distance,Euc),使用欧式距离含有约束条件的k-means聚类算法(constrained k-means with Euclidian distance,C-Euc)[16],通过凸优化算法学习得到的全局距离度量进行k-means聚类的算法(probabilistic global distance metric learning,PGDM)[4]。
与本文提出的算法类似,使用欧式距离含有约束条件的k-means聚类算法(C-Euc)也是一种常用的利用边信息的半监督聚类算法。它在传统k-means算法的基础上加上成对约束,在这些约束的“监督”下进行聚类。选择k个初始聚类中心,进入类似k-means算法的迭代过程,在迭代过程中始终要求每一步划分都满足己知的约束对信息,每个样本在没有违反成对约束条件下,被划分给最近的类,最终得到满足所有约束对信息的聚类结果[17]。
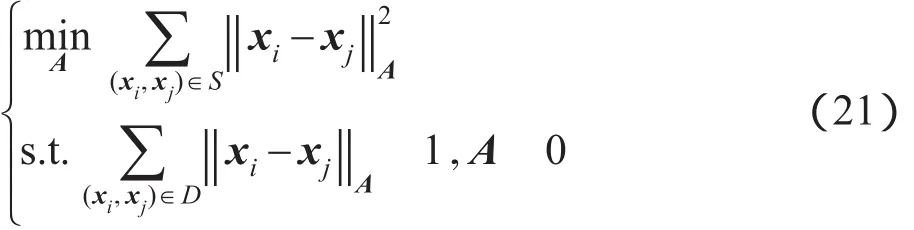
PGDM算法由Xing等人提出,是一种基于凸规划的全局距离度量学习算法。它将正约束对构成的集合记为S,负约束对构成的集合记为D。待求的距离矩阵A就可以通过以下凸规划问题进行求解:其中,||xi,xj=(xiA(xi,xj)表示两个样本点xi和xj之间的距离。根据预期得到的矩阵A的不同可以有不同的解法。如果期望得到对角形式的距离矩阵,可以通过牛顿法进行求解,本文将此算法记为PGDM-Ad(PGDM with diagonal A)。如果期待得到普通矩阵形式的距离矩阵,那么可以通过梯度下降加上逐次映射的方法进行求解,本文将此算法记为PGDM-Af(PGDM with full A)。在实验中,将学习得到的距离矩阵和其他算法一样应用于k-means聚类算法中进行评价。
4.3评价方法
为了评估聚类效果,本文采用一些标准的评价方法,包括Precision、Recall和F1[18]。定义如下:

其中,#True Positive表示将正约束对预测为正约束对的个数;#False Positive表示将负约束对预测为正约束对的个数;#False Negative表示将正约束对预测为负约束对的个数。
4.4实验结果与分析
本文所有实验均在Matlab平台下进行,所有训练数据集和测试数据集均先归一化至[0,1]区间内。对于不同的数据集和不同的算法均取相同百分比的子集构成成对约束(比如10%)。不同的距离度量均从这些成对约束中学习得到,然后均应用于k-means聚类算法中。
本文算法与其他算法实验结果对比如表2所示。表2展示了不同算法在相同的聚类中心和等量的约束对下,聚类效果的F1指标均值。每一个数据集中,对效果最好的两个算法的F1指标进行了加粗。图1展示了部分聚类效果表现优异的数据集的聚类效果图。表3展示了本文算法相对于基于欧氏距离的k-means算法聚类效果的提升率。使用如下公式计算得到:
从实验结果可以看出,本文的距离学习算法HDK-P2C和HDK-P2P在整体上有较好的表现,特别是从表3和图1中可以看出在数据集breast-cancer、wine、thyroid和segment中相对于其他算法有卓越的表现。从表2可以看出,本文算法在大多数数据集中获得了最好的表现,在利用相同数量的边信息条件下,本文提出的距离函数应用在k-means算法中的聚类效果整体上优于利用了同样边信息约束条件的CEuc算法,也优于同样是利用边信息进行距离学习的PGDM算法。
由表3可以看出,虽然本文算法在pima和dermatology数据集中只取得了次优的聚类效果,但是其相对于传统的欧氏距离仍有聚类效果的提升。由此可见,本文提出的距离学习算法得到的距离函数相对于欧式距离,在聚类应用中具有更好的表现。
结合表1和表3也可以看到,本文算法不仅对于二类数据集有较好的聚类效果,对于多类数据集也有很好的效果。比如,数据集wine为3类数据集,数据集segment为7类数据集,它们的聚类效果都取得了30%以上的提升。
在聚类算法中,由于传统的k-means聚类是无监督的聚类方法,它没有融入数据集的边信息,从而对于数据集的适应性不是很好。而C-Euc算法虽然引入了数据集的边信息,但是其使用的距离度量仍然是欧氏距离,并不适用于所有的数据集。PGDM在引入了边信息的基础上学习出了新的距离度量,但是该距离函数仍然是马氏距离的形式,属于线性的距离学习方法。本文算法不仅引入了数据的边信息,而且组合了预设的线性距离度量和非线性距离度量以形成新的距离函数,使得其对于数据集有较好的适应性。
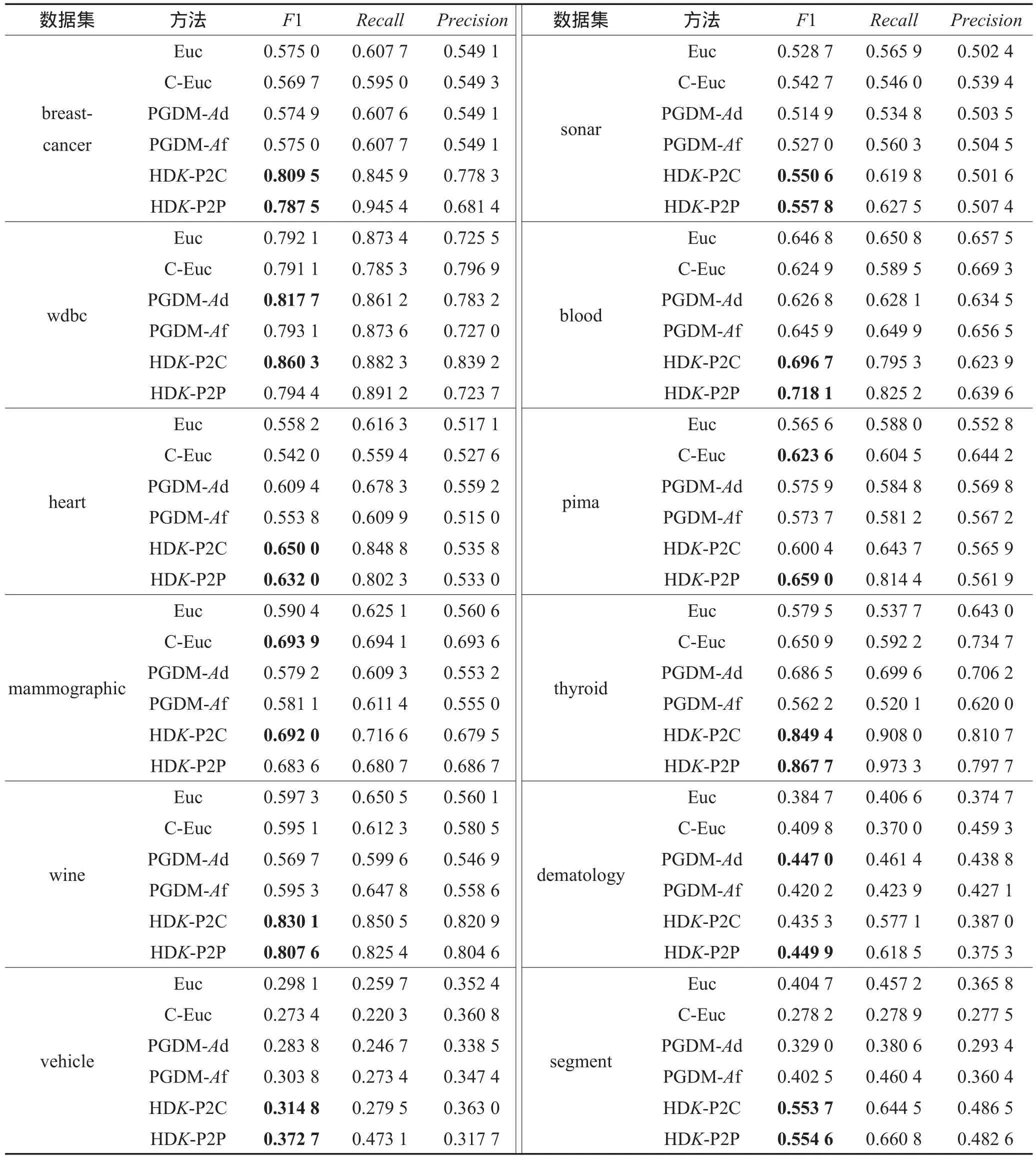
Table 2 Evaluation of clustering performance表2 聚类性能对比
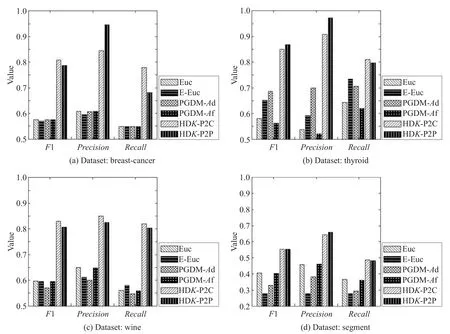
Fig.1 Clustering result of a portion of datasets图1 部分数据集的聚类效果图
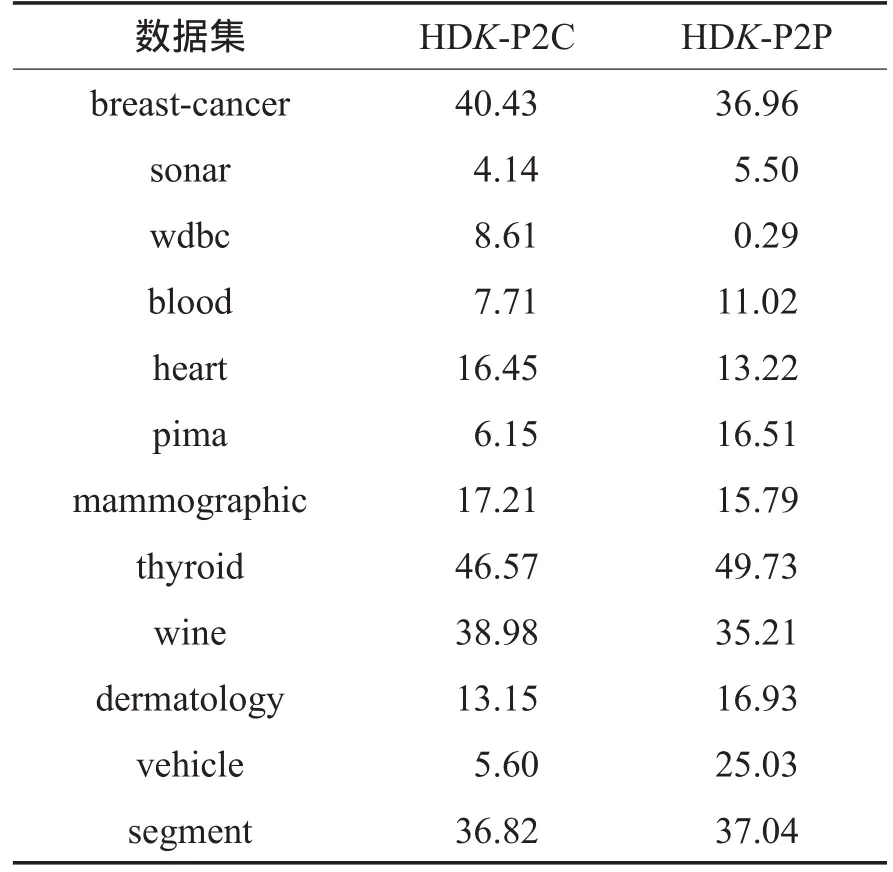
Table 3 Upgrade of this paper algorithm表3 本文算法的提升率%
表4给出了含有约束条件的k-means在采用欧式距离和本文提出的距离函数时聚类效果F1指标的对比。这两种方法均为有约束的聚类算法,其中采用混合距离的有约束条件的k-means聚类算法被表示为C-HD(constrained k-means with hybrid distance)。可以看到,总体来说在有约束条件的前提下,采用本文提出的距离函数的聚类算法在聚类效果上也具有更为优秀的表现。
为了进一步证明本文提出的混合距离在其他典型应用中也具有较好的性能,将混合距离应用在了经典分类算法——K最近邻(K-nearest neighbor,KNN)分类算法中,并与使用欧氏距离的KNN分类算法进行对比。在表5中,使用欧式距离的经典KNN算法被表示为KNN,使用混合距离的KNN算法被表示为KNN-HD(K-nearest neighbor with hybrid distance),表中的数据为分类效果的F1指标。从表5中可以看出,整体上来说,采用了混合距离的KNN算法在分类效果的表现上优于使用欧式距离的KNN算法。分类算法和聚类算法类似,都是利用距离函数来判别数据点之间的相似性,因此具有较好适应性的混合距离在分类算法上也能取得较好的效果。以上实验可以证明本文算法具有有效性。
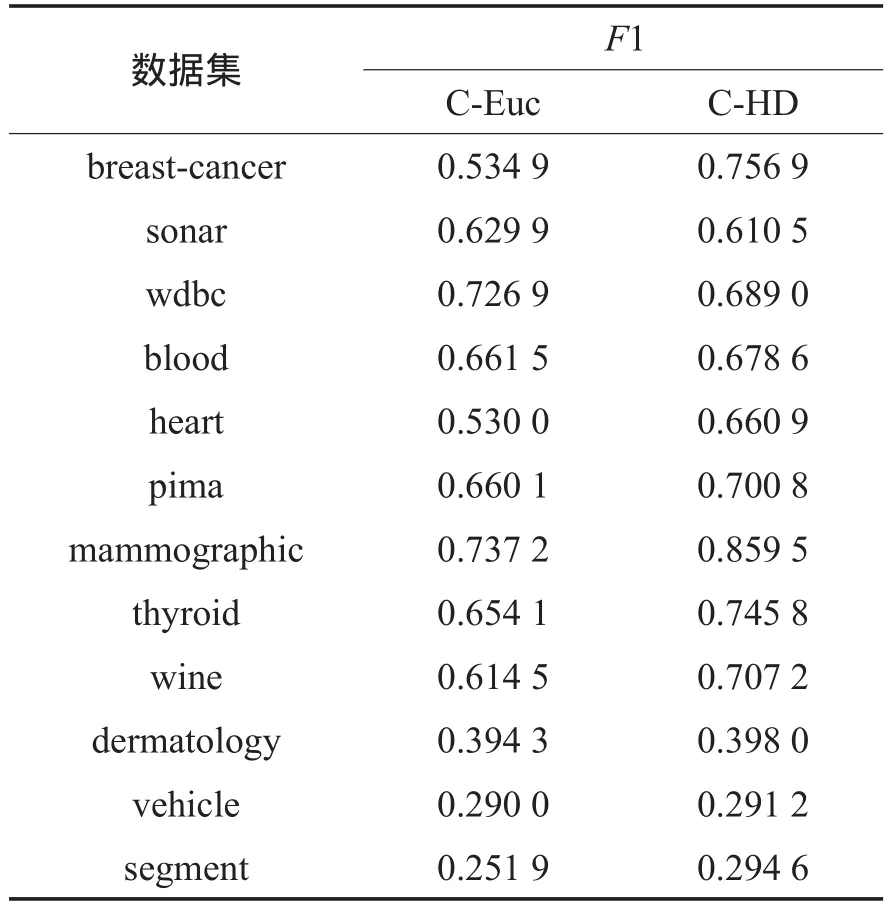
Table 4 Comparision between C-Euc and C-HD表4 C-Euc算法与C-HD算法效果对比

Table 5 Comparision between KNN and KNN-HD表5 KNN算法和KNN-HD算法效果对比
在算法性价比方面,本文算法和利用凸优化的距离学习算法(PGDM)都是利用数据的边信息学习新的距离函数,而本文算法相对于PGDM算法在时间上具有明显的优势,比如对于blood数据集,PGDM算法的平均用时为2.866 3 s,而本文算法用时为1.446 9 s。由于本文使用的是实验用的数据集,在边信息的生成上占用了一定的时间,但是在实际应用中边信息相对于明确的类标而言更易于获取。因此,本文算法在保证有效性的前提下,具有一定的性价比。
5 结束语
本文提出了一种利用边信息的混合距离学习算法。首先构建了一个由候选距离线性组合而成的距离函数模型,然后利用数据的边信息进行距离学习,得到新的距离函数,并将其应用于半监督的k-means聚类算法中检验其有效性。最后,使用UCI数据集对算法的聚类效果进行了验证,并使用F1指标来衡量,通过与其他距离学习方法和半监督聚类算法进行对比,证明了本文算法的有效性。
References:
[1] Wu Lei, Hoi S C H, Jin Rong, et al. Learning Bregman distance functions for semi-supervised clustering[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(3): 478-491.
[2] Wang Jun, Wang Shitong. Double indices FCM algorithm based on hybrid distance metric learning[J]. Journal of Software, 2010, 21(8): 1878-1888.
[3] He Ping, Xu Xiaohua, Hu Kongfa, et al. Semi-supervised clustering via multi-level random walk[J]. Pattern Recognition, 2014, 47(2): 820-832.
[4] Xing E P, Ng AY, Jordan M I, et al. Distance metric learning with application to clustering with side information[C]// Advances in Neural Information Processing Systems 15: Proceedings of the 2003 Neural Information Processing Systems, Vancouver, Canada, Dec 8-13, 2003. Cambridge, USA: MIT Press, 2003: 505-512.
[5] Bar-Hillel A, Hertz T, Shental N, et al. Learning a Mahalanobis metric from equivalence constraints[J]. Journal of Machine Learning Research, 2005, 6(12): 937-965.
[6] Hoi S C H, Liu Wei, Lyu M R, et al. Learning distance met-rics with contextual constraints for image retrieval[C]//Proceedings of the 2006 IEEE Conference on Computer Vision and Pattern Recognition, New York, USA, 2006. Piscataway, USA: IEEE, 2006: 2072-2078.
[7] Bai Liang, Liang Jiye, Dang Chuangyin, et al. A novel attribute weighting algorithm for clustering high-dimensional categorical data[J]. Pattern Recognition, 2011, 44(12): 2843-2861.
[8] Wang Jun, Wang Shitong, Deng Zhaohong.Anovel text clustering algorithm based on feature weighting distance and soft subspace learning[J]. Chinese Journal of Computers, 2012, 35(8): 1655-1665.
[9] Duda R O, Hart P E, Stork D G. Pattern classification[M]. Toronto, Canada: John Wiley & Sons, 2012.
[10] Wu K L, Yang M S. Alternative C-means clustering algorithms[J]. Pattern Recognition, 2002, 35(10): 2267-2278.
[11] Mei Jianping, Chen Lihui. Fuzzy clustering with weighted medoids for relational data[J]. Pattern Recognition, 2010, 43(5): 1964-1974.
[12] Shwartz S S, Singer Y, Pegasos N S. Primal estimated subgradient solver for SVM[J]. Mathematical Programming, 2011, 27(1): 807-814.
[13] Hartigan J A, Wong M A. A K-means clustering algorithm[J]. Applied Statistics, 1979, 28(1): 100-108.
[14] Beeferman D, Berger A. Agglomerative clustering of a search engine query log[C]//Proceedings of the 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, USA, Aug 20-23, 2000. New York, USA: ACM, 2000: 407-416.
[15] Dong Jun, Wang Suoping, Xiong Fanlun. Affinity propagation clustering based on variable- similarity measure[J]. Journal of Electronics & Information Technology, 2010, 32(3): 509-514.
[16] Wagstaff K, Cardie C, Rogers S, et al. Constrained k-means clustering with background knowledge[C]//Proceedings of the 18th International Conference on Machine Learning, Williamstown, USA, 2001. San Francisco, USA: Morgan Kaufmann Publishers Inc, 2001: 577-584.
[17] Covoes T F, Hruschka E R, Ghosh J.Astudy of K-means-based algorithms for constrained clustering[J]. Intelligent Data Analysis, 2013, 17(3): 485-505.
[18] Liu Yi, Jin Rong, Jain A K. Boostcluster: boosting clustering by pairwise constraints[C]//Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, USA, Aug 12- 15, 2007. New York, USA:ACM, 2007: 450-459.
附中文参考文献:
[2]王骏,王士同.基于混合距离学习的双指数模糊C均值算法[J].软件学报, 2010, 21(8): 1878-1888.
[8]王骏,王士同,邓赵红.特征加权距离与软子空间学习相结合的文本聚类新方法[J].计算机学报, 2012, 35(8): 1655-1665.
[15]董俊,王锁萍,熊范纶.可变相似性度量的近邻传播聚类[J].电子与信息学报, 2010, 32(3): 509-514.

GUO Yingjie was born in 1991. She is an M.S. candidate at Jiangnan University. Her research interests include data mining and artificial intelligence.郭瑛洁(1991—),女,河南信阳人,江南大学硕士研究生,主要研究领域为数据挖掘,人工智能。

WANG Shitong was born in 1964. He is a professor and Ph.D. supervisor at Jiangnan University. His research interests include artificial intelligence and pattern recognition, image processing and application.王士同(1964—),男,江苏扬州人,江南大学教授、博士生导师,主要研究领域为人工智能与模式识别,图像处理及应用。在国内外重要核心期刊上发表论文近百篇,其中SCI、EI收录50余篇,主持或参加过6项国家自然科学基金,1项国家教委优秀青年教师基金项目,其他省部级科研项目10多项。先后获国家教委、中船总公司和江苏省省部级科技进步奖5项。
Hybrid Distance Metric Learning Method with Side-Informationƽ
GUO Yingjie+, WANG Shitong
School of Digital Media, Jiangnan University, Wuxi, Jiangsu 214122, China
+ Corresponding author: E-mail: ying_dm@163.com
GUO Yingjie, WANG Shitong. Hybrid distance metric learning method with side- infomation. Journal of Frontiers of Computer Science and Technology, 2016, 10(3):414-424.
Abstract:Learning distance function with side-information plays a key role in many data mining applications. Conventional metric learning approaches often use the distance function which is represented in form of Mahalanbobis distance which has some limitations. This paper proposes a new metric learning method with hybrid distance. In detail, the unknown distance metric is represented as the linear combination of several candidate distance metrics. A new distance function is achieved by learning weights with side-information. This paper applies the new distance function into clustering algorithm to verify the effectiveness. It also chooses the datasets from UCI machine learning repository to do experiments. The comparison with approaches for learning distance functions with side-information reveals the advantages of the proposed techniques.
Key words:distance metric learning; hybrid distance metric; distance function; side-information
doi:10.3778/j.issn.1673-9418.1505005
文献标志码:A
中图分类号:TP181

