广义变分不等式解的精炼*

赵渊嫣，杨　辉，陈　莎

(贵州大学理学院 ，贵州　贵阳　550025)



广义变分不等式解的精炼*

赵渊嫣，杨辉，陈莎

(贵州大学理学院 ，贵州贵阳550025)

摘要：主要通过对集值映射Φ的定义域X和法锥映射进行扰动，对Φ的广义变分不等式的解进行精炼，进一步提出稳定解和法锥稳定解的定义，并证明其存在性结果。

关键词：广义变分不等式；精炼；定义域；法锥映射

0引言

设X是n维欧氏空间Rn的一个子集，是X到Rn的映射。 如果存在x*∈X满足：

(x*-x)T(x*)≥0，∀x∈X

则称x*为关于的变分不等式的解，其中：aTb表示向量a∈Rn和b∈Rn的内积。

众所周知，变分不等式的问题在很多领域都有重要的应用，特别是在a∈Rn非合作博弈、经济平衡理论、不动点理论、非线性最优化理论和交通网络均衡[1-4]中。而在这些应用中，解往往都不是唯一的，所以需要对解进行精炼[5-6]。

广义变分不等式问题如下：

设X是Rn的一个子集，Φ：X→P0(Rn)为集值映射。 这里，P0(Rn)表示Rn中所有非空子集。如果存在x*∈X，z∈Φ(x*)使得：

(x*-x)Tz≥0， ∀x∈X

则称x*为关于Φ的广义变分不等式的解。

而关于Φ的广义变分不等式的解的存在性，在文[8]中已有相关结果： 即X是Rn的非空紧凸子集，Φ：X→P0(Rn)为上半连续的集值映射，且∀x∈X，Φ(x)是Rn中的紧凸集。

广义变分不等式中，其解通常是不唯一的，所以需要对其进行精炼，以满足应用的需求。

在var der Laan，Talman和Yang[9]的文章中，提出了变分不等式解的一种精炼方法，在此将之推广到广义变分不等式中。

本文主要是借助一列扰动，去掉那些不符合要求的解，且至少保留一个解，称之为稳定解。 精炼的主要思想是通过对Φ的定义域X和法锥的扰动来剔除不稳定的解，以实现解的精炼。

1主要结果

在这部分中，基于定义域和法锥映射的扰动，提出广义变分不等式的稳定解和法锥稳定解，并证明其存在性。

首先，介绍一些基本知识。

设X是n维欧氏空间Rn的一个非空紧凸子集，A(X)为X的仿射包。为了不失一般性，对给定正整数m(0≤m≤n)，假定A(X)是一个Rn的(n-m)维的仿射子空间，且表示为：

A(X)={x∈RnCTx=d}

其中，C是n×m的满秩矩阵，d是一个m维向量。 当m=0时，A(X)=Rn。 设Rn的线性子空间为Y={y∈Rny=Cv，v∈Rm}。 当m=0，则Y是零向量。

给定A(X)中的(n-m)维紧凸子集Z，Z在点x∈Z的法锥映射表示为：

则N(Z，·)是Z上的上半连续集值映射，由文[10]显然可得。

对∀x∈Z，N(Z，x)是包含Y的闭凸锥。 且当x属于Z的相对内部时，N(Z，x)=Y。 显然，x*∈Z是关于Φ的广义变分不等式的解当且仅当Φ(x*)∩N(Z，x*)≠φ。

为了讨论广义变分不等式解的精炼，我们引进两个集值映射：χ和G。

设映射χ：[0,1]→X为关于集合X的扰动，且满足以下两个条件：

(X1)映射χ：[0,1]→X是连续的，且对∀ε∈[0,1]，集合χ(ε)是X的非空紧凸子集。

(X2)χ(0)=X，且∀ε和ε′(0≤ε<ε′≤1)，都有χ(ε′)⊂Intχ(ε)。

其中，IntA表示集合A⊂X的相对内部。

通过以下两个例子，我们可以更好地理解χ映射关于定义域X的扰动。

例2.2设χ(ε)=ε{v}+(1-ε)X，v属于X的相对内部。 对每一个x∈Xχ(1)，都存在唯一的ε(0≤ε<1)，使得x属于χ(ε)的相对边界。

给定满足(X1)，(X2)的映射χ，设映射G：X→P0(Rn)满足如下的三个条件：

(G1)G是上半连续的，且∀x∈X，G(x)是包含Y的闭凸锥。

(G2)对任意x∈Bndχ(ε)和y∈N(χ(ε)，x) {0n}，0<ε<1，存在ω∈G(x)，使得yTω>0，其中BndA表示集合A⊂X的相对边界。

(G3)对任意x∈BndX，都有G(x)⊆N(X，x)。

以上条件说明，当x在集合χ(ε)的边界上时，集合G(x)是包含Y的一个锥。对任意非零向量y∈N(χ(ε)，x)，存在一个向量ε∈G(x)与y成锐角。 如果x在集合X的边界，则G(x)是法锥N(X，x)的一个子集。

定义2.3如果一对映射(χ，G)满足(X1)，(X2)，(G1)，(G2)和(G3)，则称这对映射是正则的。

给定一对映射(χ，G)和ε(0≤ε<1)，定义Gε：

χ(ε)→Rn如下：

给定集值映射Φ：X→P0(Rn)，如果存在集值映射G：X→P0(Rn)和点x∈X，使得G(x)∩Φ(x)≠φ，则称点x为映射G(x)和Φ(x)的重合点，称映射G(x)为关于Φ的重合映射。

关于讨论广义变分不等式的稳定解，首先给出集值映射Φ的ε-稳定解的概念。

定义2.4给定一对映射(χ，G)和ε(0≤ε<1)，如果x∈χ(ε)，z∈Ф(x)使得z∈Gε(x)，则称点x∈X是集值映射Φ关于(χ，G)的ε-稳定解。

由此可以看出，集值映射Φ关于(χ，G)的ε-稳定解是Φ和Gε(x)的重合点。当ε-稳定解x在χ(ε)内部，Φ(x)∩Y≠φ；x在χ(ε)的边界时，Φ(x)∩G(x)≠φ，而Y⊂G(x) ，所以G(x)为关于Φ的重合映射。 特别当ε=0时，集值映射Φ的ε-稳定解x是Φ的广义变分不等式的解。

广义变分不等式的稳定解定义如下：

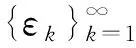
b)对∀k，xk是集值映射Φ关于(χ，G)的εk-稳定解；

则称x*关于(χ，G)是稳定的(简写成(χ，G)-稳定)。

一个(χ,G)-稳定解x*不管是在X的内部还是边界，在它的任意一个邻域内，都存在一个点x∈X，使得Φ(x)∩G(x)≠φ。

关于集值映射Φ的广义变分不等式的稳定解，其存在性结果如下：

定理2.6设集值映射Φ：X→P0(Rn)上半连续，且∀x∈X，Φ(x)是Rn中的紧凸集，(χ，G)是一对正则的映射，则在X上一定存在(χ，G)-稳定解。

证明：首先要证明对任意的ε(0<ε<1)，Φ关于(χ，G)的ε-稳定解存在。 给定ε(0<ε<1)，由(G1)可知Gε上半连续，且对任意x∈χ(ε)，Gε(x)是非空闭凸集。 因为对所有的x∈X，集合G(x)是一个锥，由(G2)知，对任意x∈Bndχ(ε)和y∈N(χ(ε)，x)，存在ω∈Gε(x)和z∈Φ(x)，满足yTω≥yTz。 根据Ky Fan重合定理[11]可以知道当映射Φ(·)和Gε(·)限制在非空紧凸集χ(ε)上时，存在重合点的xε∈χ(ε)满足Φ(xε)∩Gε(xε)≠φ。 因此，当

xε∈Intx(ε)时，Φ(xε)∩Y≠φ

xε∈Bndχ(ε)时，Φ(xε)∩G(xε)≠φ

即xε是Φ的关于(χ，G)的ε-稳定解。

当x*属于X的内部时，由χ的连续性及(X2)可知，当k足够大时，点列xk∈Intχ(εk)，由此可知，存在zk∈Φ(xk)，使得zk∈Y，因此存在z∈Φ(x*)，使得z∈Y，即x*是Φ的解。当x*属于X的边界时，且k足够大时，点列xk∈Bndχ(εk)。 因此，对每一个k∈N，Φ(xk)∩G(xk)≠φ。 因为Φ上半连续，G也是上半连续，且xk收敛于x*，可以得到Φ(x*)∩G(x*)≠φ。 由(G3)可知，Φ(x*)∩N(X，x*)≠φ，即x*是Φ的广义变分不等式的解。

最后，考虑广义变分不等式的法锥稳定解。

定义2.7给定集值映射Φ：X→P0(Rn)和一对映射(χ，G)，如G是关于χ的法锥映射，则称(χ，G)-稳定解x为关于χ是法锥稳定的(简写为χ-法锥稳定)。

定理2.8设映射χ满足(X1)和(X2)，G是关于χ的法锥映射，则(χ，G)是正则的。

证明：由于法锥映射G满足(G1)，(G2)和(G3)，则定理显然可证。

推论2.9设集值映射Φ：X→P0(Rn)上半连续，且任意x∈X，Φ(x)是Rn中的紧凸集。χ：[0,1]→X是满足(X1)和(X2)的映射，则Φ在X上一定存在χ-法锥稳定解。

参考文献【REFERENCES】

[1]QH.Ansari，JC.Yao，A fixed point theorem and its appli—cations to a system of variational inequalities[J].Bull.Anstral.Math.Soc，1999，59(3)：422—433.

[2]Z.Fang A generalized vector variational inequality probl—em with a set—valued semimomntone mapping[J].Nonlinear Analysis，2008，69(5)：1824—1829.

[3]徐庆，朱道立，鲁其辉.Nash均衡、变分不等式和广义均衡问题的关系[J].管理科学学报，2005，8(3)：1—7.

XU Q，ZHU D L，LU Q H.Relations among nash equilbrium，variational inequalities and generalized equilibrium problem[J].Journal of management sciences in China，2005，8(3)：1—7.

[4]陆化普，殷亚峰.交通网络均衡分析的变分不等式方法[J].公路交通科技，1997(2)24—29.

LU H P， YIN Y F. A method of variational inequality for analysing the urban traffic network equilicrium[J].Journal of highway and transportation research and development，1997(2)24—29.

[5]E.E.C.Van Damme.Stability and perfection of nash equilibria[M].Springer—Verlag，Berlin，1987：317.

[6]T M Kehoe.Computation and multiciplicity of equilibria[C].in Handbook of Mathematical Economics，Vol.IV，W.Hildenbrand and H.Sonnenschein，eds，North—holland，Amsterdam，1991：2049—2143.

[7]张从军.集值B_H_S变分不等式及其应用[J].工科数学，1995(4)35—41.

ZHANG C J.Variational inequality for set—valued B_H_S mapping with applications[J].Journal ofmathematics for technology，1995(4)35—41.

[8]俞建.博弈论与非线性分析[M].北京：科学出版社，2008：222.

Yu J. Game theory and non—linear analysis[M].Beijing：Science Press，2008：222.

[9]G V Laan，D Talman ，Z.Yang.Refinements of stationary points with applications to noncooperative games and economics[J].Siam Journal on Optimization，2006，16(3)：854—870.

[10]方嘉琳.集值映射的连续性与连通性[J].四平师院学报(自然科学版)，1979：3—8.

FANG J L.Continuity and connectedness of point—to—set mapping[J].Journal of Siping teachers college(Natural science edition)，1979：3—8.

[11]A J J Talman，Z Yang.A constructive proof of Ky Fan’s coincidence theorem[J].Mathematical Programming，2009，118(2)：317—325.

投稿日期：2016-01-06；修回日期：

Refinements of solutions to generalized variational inequalities

ZHAO Yuanyan，YANG Hui，CHEN Sha

(CollegeofScience，GuizhouUniversity，Guiyang550025，China)

Abstract：In this paper，the domain X and the normal cone are perturbed to refine the solutions of generalized variational inequalities with respect to point—to—set mapping Φ.Further，the concepts of stable solution and normal—stable solution are introduced，and their existence results are proved.

Keywords：generalized variational inequalities；refinements；domain；normal cone mapping

中图分类号：O 177.92；O 178；O 29

文献标识码：A

文章编号：1003—6563(2016)02—0049—03

*基金项目：国家自然科学基金项目“多目标群体博奕与进化的动力学的研究和应用”，课题编号：11271098。

作者简介：赵渊嫣(1990-)，女，贵州大学理学院数学系硕士研究生。研究方向：应用数学。