椎弓根螺钉直径、长度变化对脊椎应力影响的三维有限元分析

田　野，汤　耿，伍　权，徐卫平

(1贵州大学　机械工程学院，贵州　贵阳　550025；2贵州师范大学 机械与电气工程学院，贵州　贵阳　550001)



椎弓根螺钉直径、长度变化对脊椎应力影响的三维有限元分析

田野1，汤耿2，伍权2，徐卫平2

(1贵州大学机械工程学院，贵州贵阳550025；2贵州师范大学 机械与电气工程学院，贵州贵阳550001)

摘要：在 CT图像的基础上利用Mimics 软件完成脊椎轮廓三维重建，通过3—matic模块对模型进行光滑处理并以iges格式导入 UG 软件中进一步构建椎体曲面模型，并利用缝合及建模相关功能完成脊椎模型的三维重构；通过UG软件进行网格划分，设置材料属性，添加边界条件及载荷并进行有限元分析，完成螺钉内固定应力分析；椎弓根螺钉直径在3.5 ～ 5.5 mm 范围变化时，随着螺钉直径的增大有利于改善脊椎骨应力的大小；随着螺钉长度变化，脊椎骨应力的大小变化不明显。

关键词：脊椎；三维重建；有限元分析；应力

0引言

脊柱为人体的中轴骨骼，是身体的支柱，有负重、减震、保护和运动等功能。随着椎弓根钉棒系统的发展，对于退变、肿瘤、创伤和畸形等胸腰椎疾病，椎弓根螺钉固定已经成为维持脊椎稳定性的一个主要方式。影响椎弓根螺钉稳定性的因素主要有螺钉的长度、直径；从生物力学角度讲，直径较大、长度较长的椎弓根螺钉能提供更有力的固定强度，但螺钉导致椎弓根的膨胀或内壁破损有使椎管直径变小的潜在可能，将可能引起脊髓或神经受压；因而在不同长度、直径椎弓根螺钉影响下，有必要对脊椎的力学分布影响进行分析，为临床选择和设计椎弓根螺钉提供理论依据。

随着有限元分析技术的迅猛发展，其计算精确度得到了不断提高，仿真结果能够和工程实践高度吻合，在工程实践进行前对其有极大的指导意义[1，2，3]；有限元分析法在计算复杂形状、载荷和材料性能方面的优异能力，随着与传统医学的结合，让各类临床医生从临床角度出发，针对不同的问题建立不同仿真模型，用来模拟分析各种临床实际问题，可方便实现实验的可重复性与患者个性化，能有效的提供针对性的手术方案。NX UG拥有一体化建模、分析的强大功能，避免在不同软件之间进行模型数据传递的失真问题[4]；因此，基于NX UG进行模型的三维重建与有限元分析，从生物力学角度，可为椎弓根螺钉设计研究提供参考。

1脊椎三维重建

1.1技术路线

逆向工程技术中的关键技术之一是曲面重构技术，人体骨关节模型重构面向的是个性化假体制作、生物力学分析、手术方案模拟、假体设计，它的应用与研究均是以骨骼的三维模型为基础。由于人体骨骼一般均为复杂曲面，而脊椎的曲面更为复杂，结合这一特点，本文给出了如图1所示的逆向设计路线。

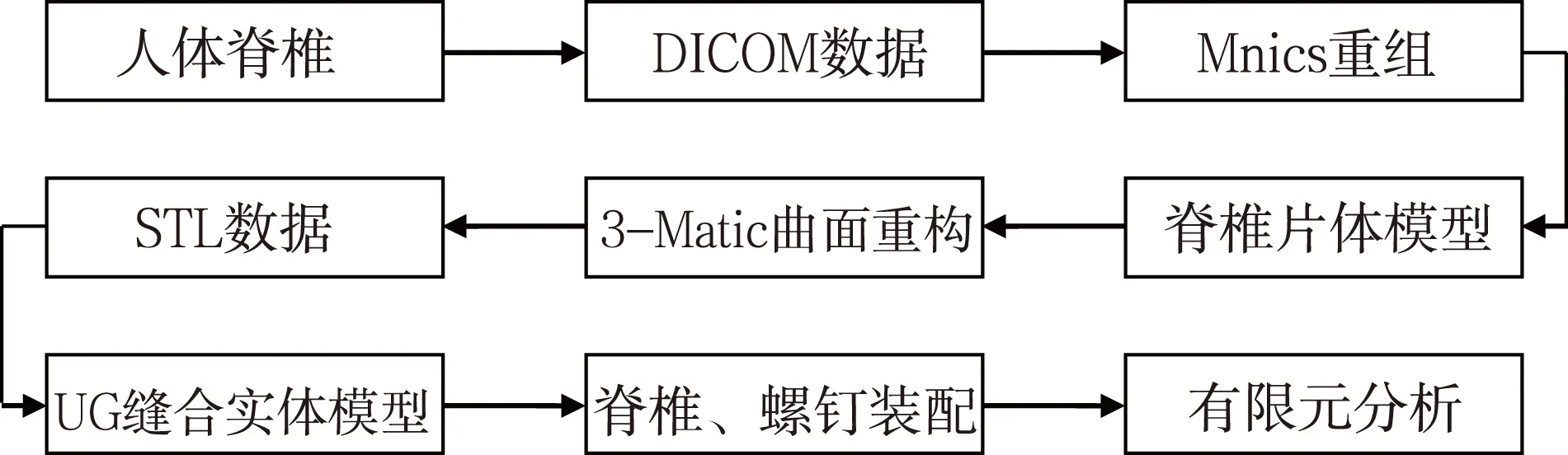
图1　脊椎逆向设计路线

1.2椎体模型三维重建

首先，使用CT扫描获取脊椎部位CT图像并以DICOM格式存储，然后导入到Mimics设计环境下，通过图像识别与分割技术，将软组织与骨骼部分进行分离，填充内部与外部不连通的孔洞和修缘；通过 Calculate—3D工具，选择相应的蒙板并设置质量参数，把二维数据文件进行堆叠，然后完成椎体的三维重建；生成STL三维模型。并在3—matic中将生成的三维模型进行光滑处理，生成具有较好面网格质量的模型以方便后续处理。此时，导出模型存在缺陷，可以继续导入到正向设计软件UG中缝合成可进一步处理的实体模型、并完成脊椎与螺钉的装配；基本流程如图2所示。

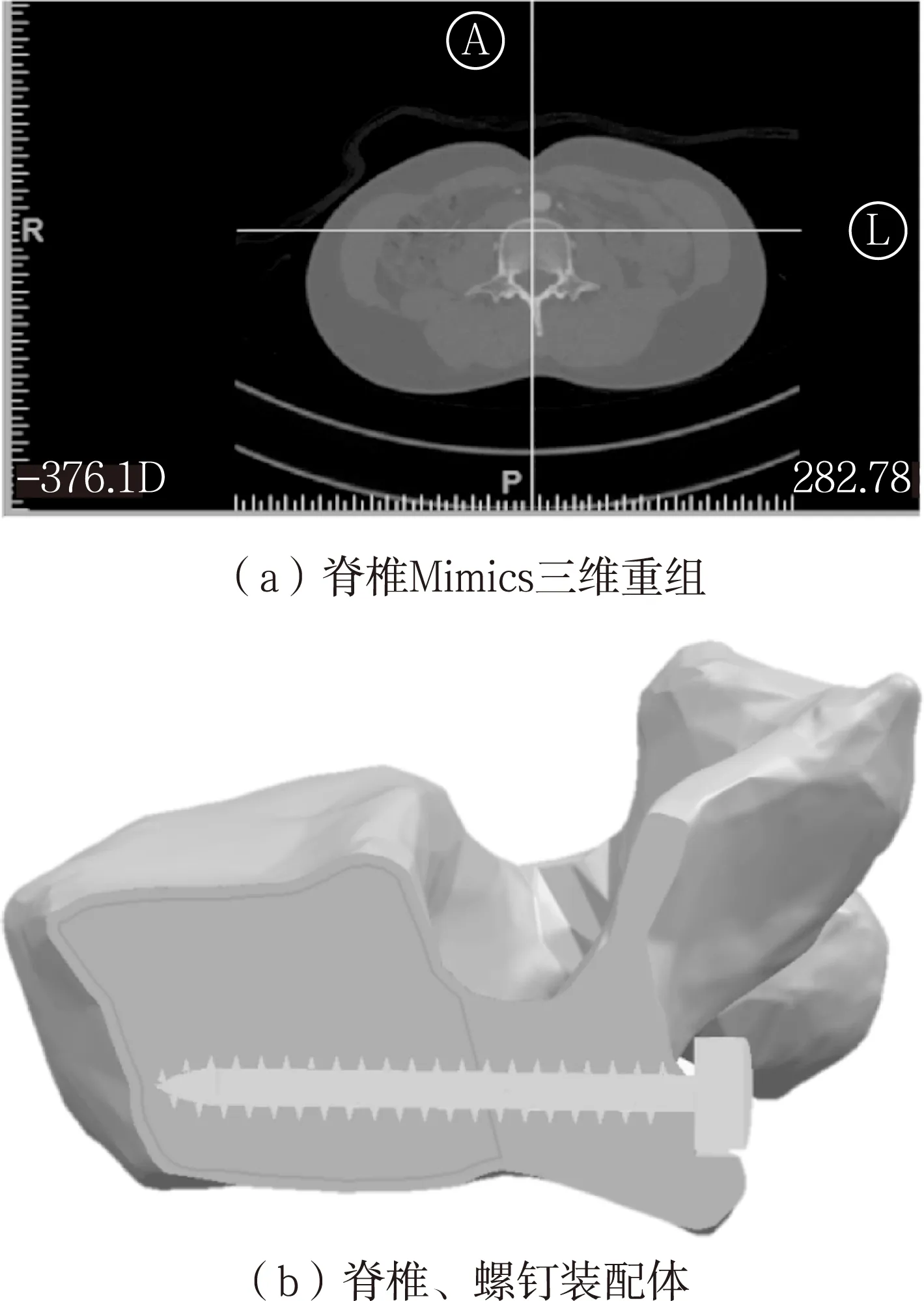
图2　椎体模型重构

2有限元分析及验证

2.1仿真分析理论基础

有限元分析法遵循由整体到分块，再从分块到整体，采用分块近似插值函数去逼近整体连续函数，使连续体力学问题得到整体离散逼近、分块连续的近似解，从而得到较精确的计算结果[5]基本遵循3个方程，利用弹性力学的几何方程写出单元应变εe与节点位移的关系矩阵，称应变矩阵B即：

εe=Bδe

(1)

由材料的物理方程，得到单元弹性矩阵[D]，从而推出用节点位移表示单元应力：

{σ}e=[D]εe=[D][B][δ]e

(2)

然后考虑节点平衡求得单元节点力与节点位移的关系，由矩阵[K]表示，称单元刚度矩阵。利用变分原理，建立作用于单元上的节点力与节点位移之间的关系式，即单元的平衡方程：

(3)

2.2前处理

2.2.1材料属性设置和网格划分

有限元模型中各部分材料赋值均为真实成年人体骨骼解剖结构材料值[6]，如表1所示，由于椎弓根及棘突内松质骨含量很低，故设定松质骨主要存在于椎体内，然后在椎体模型上模拟1 mm厚的密质骨。将各部位材料的弹性模量、泊松比等材料系数及特征值输入模型。

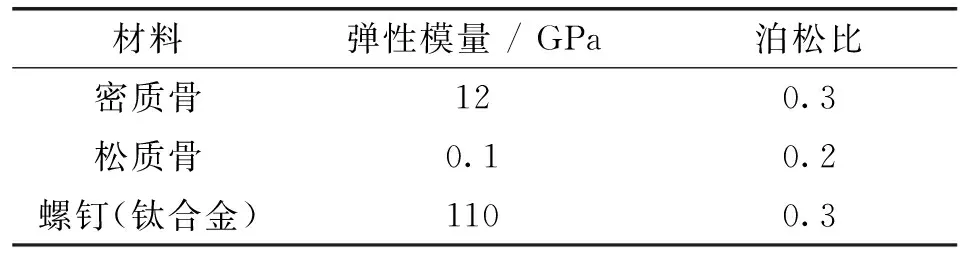
表1　有限元模型各结构材料常数

分别对脊椎与螺钉模型进行网格划分，采用自带的3D 四面体自动网格划分，其类型是 CTETRA10节点四面体网格；由于模型较为复杂，有较多尖锐的局部细小特征，故采用自动修复有故障单元[7]，网格划分完成后如图3(a)所示。

2.2.2载荷及边界条件

本实验采用NX Nastran 求解器进行求解，选择求解器类型为结构分析，求解器类型为静力分析，椎体模型下表面添加固定约束，在螺钉上添加用户自定义约束以约束螺钉沿径向、切向的平移自由度，沿螺钉轴向施加250N载荷如图3(b)所示；面接触作为一种连接方式在工程中非常常见，严格意义上讲，面接触具有非线性特点，但是为了简化问题、简化求解规模，如果面接触之间处于微小的弹变范畴，当做线性处理也能保证模拟接触状态的精度，这样的处理在工程中具有大量的背景，故在脊椎与螺钉接触面之间定义“曲面与曲面接触”[8]。

2.3仿真结果及分析

由于螺钉长度与直径有相应的标准系列，在螺钉直径分别为3.5 mm、4 mm、4.5 mm、5 mm、5.5 mm、6 mm，螺钉长度在20 mm、25 mm、30 mm、35 mm、40 mm间变化时，有30种螺钉长度与直径组合，对30种组合数据分别进行解算，分别得到30组不同数据，其最大von Mises应力分别出现在第一节螺纹处、椎弓根中间最小截面处，其分布云图如图3(c)、(d)所示。

螺钉直径在3.5～5.5 mm之间变化时，随着螺钉长度改变，最大应力出现在脊椎第一节螺纹处，如图3(c)所示；螺钉直径达到6 mm时，随着螺钉长度改变，最大应力出现在脊椎椎弓根中间最小截面处，如图3(d)所示。

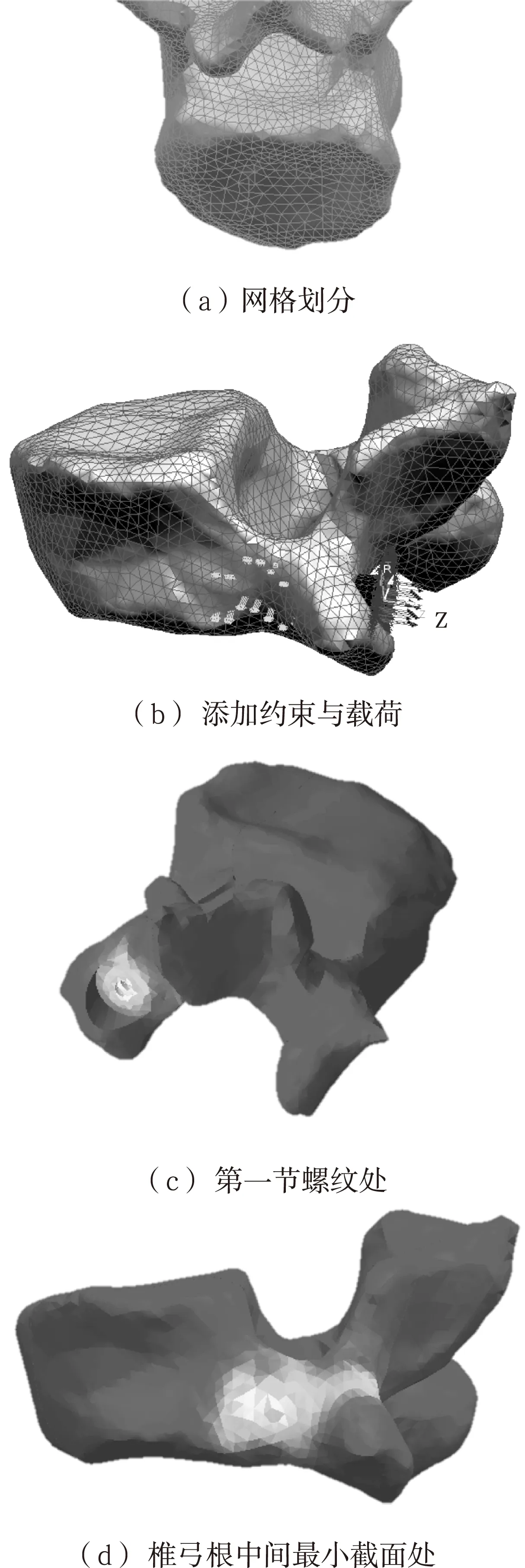
图　3　有限元分析流程及结果

当直径在3.5 ～5.5 mm之间，螺钉直径一定的情况下，随着螺钉长度增加，脊椎所受最大应力逐渐减小；螺钉直径为6 mm时，随着长度增加，脊椎应力大小呈现先增大后减小趋势，其变化如图4(a)所示；螺钉长度一定的情况下，长度为40 mm时，随着直径增加，脊椎应力大小呈现减小趋势，减小程度较大；长度在20 ～35 mm时，当直径在3.5～5.5 mm间增加，脊椎应力大小呈现减小趋势，减小程度较大，当直径增大到6 mm时，脊椎应力大小反而增大，其变化如图4(b)所示。

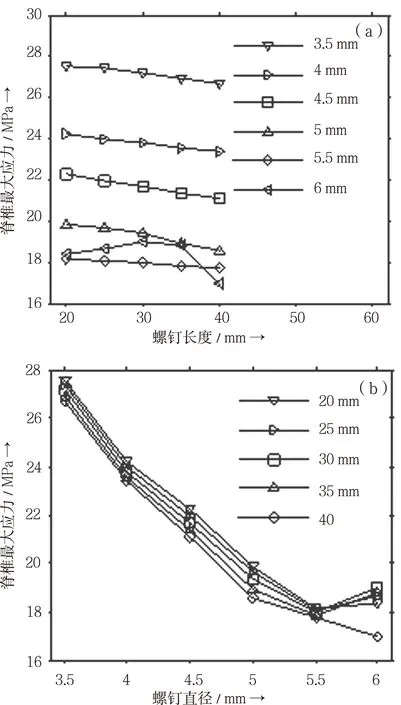
图4　脊椎应力图

3结论

1)对于直径相同的螺钉，螺钉长度变化对脊椎应力分布情况及大小的改变不显著，随着长度增加，脊椎应力大小整体呈现减小趋势，最大应力出现在脊椎第一节螺纹处；当螺钉直径为6 mm时，最大应力出现位置从脊椎第一圈螺纹处变化为脊椎椎弓根中间最小截面处。

2)对于长度相同的螺钉，螺钉直径变化对脊椎应力分布情况及大小的改变显著，螺钉直径在3.5～5.5 mm之间增加，脊椎应力大小呈现减小趋势；随着直径进一步增大为6 mm，由于椎弓根最小截面处整体刚度、强度降低，应力突然增大，最大应力位置从脊椎第一圈螺纹处变为脊椎椎弓根中间最小截面处。

3)在选择螺钉时，螺钉长度增加，脊椎的应力的分布与大小变化较小；随着直径在一定范围内增加，脊椎应力有明显降低，但直径太大，降低椎弓根小截面处的刚度与强度，故应力反而增加；故直径在3.5～5.5 mm之间，选择大直径螺钉有利于提高螺钉椎体连接强度，不必刻意增加螺钉长度。

参考文献【REFERENCES】

[1]郭松青.基于CT图像建立人体足部骨骼三维有限元模型的研究[D].合肥工业大学，2006.

GUO S Q.Research on the 3—dimensional finite element modeli—ng of human foot—skeleton based on CT images[J].Journal of Hefei University，2006.

[2]张美超，张志凌，夏虹，赵卫东.枢椎齿突骨折的有限元分析[J].中国临床解剖学杂志，2005，23(1)：96—99.

ZHANG M C，ZHNG Z L，XIA H，ZHAO W D.Analysis of axis odontoid fracture on a finite element model[J].chinese journal of clinical anatomy，2005，23(1)：96—99.

[3]陈琼.三维有限元建模方法的研究现状[J].口腔医学，2006，26(2)：154—155.

CHEN Q.Applied situation of finite element modeling method[J].Stomatology，2006，26(2)：154—155.

[4]宋志国，吴云飞.UG 应用教程[M].北京：电子工业出版社，2003.

SONG Z G，WU Y F.The tutorials of UG[M].BEI JING：Electronic Industry Press，2003.

[5]侯炜.汽车车架的有限元静动态响应分析[D].秦皇岛：燕山大学，2006.

HOU W.Static and dynamic response analysis of frame by finite element method[D].QINGHUANGDAO：Yanshan University，2006.

[6]ZHONG Z C，WANG J P.Finite element analysis of thelumbar spine with a new cage using a topology optimization method[J].Medical Engineering and Physics，2006，28(1)：90—98.

[7]胡仁喜，康士廷.UG NX 8. 0 动力学与有限元分析从入门到精通[M].北京：机械工业出版社，2012.

[8]沈春根，王贵成，王树林.UG NX7.0有限元分析入门与实例精讲[M].北京：机械工业出版社，2010：63—69.

投稿日期：2015-11-16；修回日期：2015-11-17

Three dimensional finite element analysis of stress distribution on continuously varying of diameter and length of pedicle screw

TIAN Ye1，TANG Geng2，WU Quan2，XU Weiping2

(1CollegeofMechanicalEngineering，GuizhouUniversity，Guiyang550025，China；2CollegeofMechanicalEngineering，GuizhouNormalUniversity，Guiyang550001，China)

Abstract：3—D contour model is generated by Mimics software based on the CT image.The model is smoothed by 3—matic module and imported into the UG software with iges format file.The 3D reconstruction of the spine model is completed by using the suture and modeling related functions.The stress analysis of the screw internal fixation is completed by dividing grid with the UG software，setting up the material properties，adding boundary conditions and finite element analysis.While the diameter of screw is in range from 3.5 mm to 5.5 mm，it could improve the value of stress on the spinal column with the increase of pedicle screw diameter.The variation of stresses of vertebra is not obvious with the changing of screw diameter.

Keywords：spinal column；3—D reconstruction；finite element analysis；stress

中图分类号：TH 16；R 319

文献标识码：A

文章编号：1003—6563(2016)02—0074—04

作者简介：田野(1989-)，男，硕士研究生。研究方向：先进制造技术。

通讯作者：▲徐卫平(1967-)，男，教授，硕士生导师。研究方向：先进制造技术。