基于TVM的西北江三角洲地区非一致性洪水频率分析*

刘丙军，邱凯华,2，廖叶颖

(1.中山大学地理科学与规划学院，广东 广州510275；2. 广东省水文局，广东 广州510150)

基于TVM的西北江三角洲地区非一致性洪水频率分析*

刘丙军1，邱凯华1,2，廖叶颖1

(1.中山大学地理科学与规划学院，广东 广州510275；2. 广东省水文局，广东 广州510150)

为探讨非一致性洪水频率分析方法，选取1960-2009年西北江三角洲主要控制水文站马口站和三水站逐年最大日流量序列，运用基于时变矩(TVM)的方法，研究了西北江三角洲地区非一致性洪水频率分析问题，就指定设计流量下重现期变化和指定重现期下设计流量变化进行分析，揭示了变化环境背景下设计洪水的响应规律，并与传统水文频率分析方法结果进行对比，结果表明：① TVM方法考虑到水文序列特征参数随时间发生变化，能较好反映变化环境下水文要素特征值的非一致性特征；② 西北江三角洲马口站和三水站指定流量标准下重现期越来越短，而指定重现期标准下设计流量值越来越大，这一现象与近年来该地区极端水文事件频发的事实相符。

西北江三角洲；洪水频率；非一致性；时变矩

西北江三角洲地区地势低平、河网纵横、经济发达、人口密集、城镇集中，在快速城市化、典型人类活动(上游水利工程调度与河道挖沙)、海平面上升等多重复杂、不确定性因素影响下，该地区降雨、径流等水文要素发生显著变异，水文极值和特征值偏离常规，同一断面水量频率与水位频率不对应，同一次水文事件上下游水文要素频率不一致等等，水文序列一致性遭到严重破坏。尤其是近年来河道挖沙导致西北江三角洲中上游河段冲刷下切、下段淤积，河道比降明显变小，西江、北江分流比发生重大改变，造成上游水文控制站马口站和三水站洪水过程一致性受到严重破坏[1-2]。开展变化环境下西北江三角洲地区非一致洪水频率分析，对揭示该地区洪水过程变异特征，指导水利工程建设具有重要理论和实践意义。

当前，非一致性水文频率分析的主要方法有直接分析法，包括基于混合分布的非一致性水文频率分析方法[3]、基于条件概率分布的非一致性水文频率分析方法[4]，以及基于时变矩的水文频率分析方法等[5-8]。不同方法有不同的适用条件，如基于混合分布的非一致性水文频率分析方法考虑了水文要素变异前后的非同分布问题，但因分布函数和参数较多，估算困难；基于条件概率分布的非一致性水文频率分析方法则利用条件概率定义水文概率密度分布函数，适用于因数据缺失、气候差异等造成的非一致性水文序列频率分析；基于时变矩的水文频率分析方法则通过改变不同时期水文序列分布函数的参数值，反映外界环境对水文要素的影响，可体现时间序列统计分布随时间的变化情况，该方法已广泛运用于水文要素频率非一致性分析。叶长青等[9]采用时变矩模型对坪石站和龙川站年最大日流量序列进行非平稳性处理，探讨不同变化环境背景下武江流域和东江流域非一致性洪水频率的响应规律；杜涛等[10]选取时间为协变量，研究了渭河流域暴雨时间序列统计分布随时间的变化情况，结果表明未来时期的设计暴雨量级有显著增大的趋势；刘德地和杜佩玲[11]基于时变矩水文频率分析法对东江流域龙川站的年最大洪峰流量的重现期进行计算，得到序列呈下降趋势，原有同等防洪能力重现期增大。

综上分析，本文针对非一致性水文序列特征参数随时间变化的特点，选取1960-2009年西北江三角洲主要水文控制站马口站和三水站逐日洪水过程，运用基于时变矩(TVM)的分析方法，研究了该地区洪水频率的非一致性问题，并与传统水文分析方法相比，探讨了TVM分析方法的适用性，旨在为丰富变化环境下水文要素变异分析理论、完善该地区水文时频分析研究成果提供一定理论和实践依据。

1 研究区与数据

西北江三角洲网河区主要由西江水系、北江水系组成。西江干流至思贤滘长2 075 km，集雨面积35.3万km2，北江干流至思贤滘长468 km，集雨面积4.7万km2，西江、北江在思贤滘相互贯通，组合进入西北江三角洲网河区(图1)。该地区受东南季风和西南季风影响，属于湿热多雨的亚热带气候，多年平均气温14～22 ℃，多年平均降水量约为1 760～2 325 mm，西江多年平均年径流量为2 322亿m3，北江多年平均年径流量为451亿m3。

图1 西北江三角洲地区水系图Fig.1 The river network of the study area

西北江三角洲上游西江、北江流域形状呈蒲扇形、支流多、集水面积大、集流时间长，洪水峰型肥胖，呈现锋高、量大、来势猛、高水持续时间长的特点。洪水主要受锋面暴雨和热带气旋造成，发生时间集中在6-10月，约占年径流总量的80%。

本次研究选取的数据为马口站和三水站历史年最大日流量序列，时间序列为1960-2009年，序列长度为50 a。水文资料主要来自水文统计年鉴。

2 研究方法

变化环境下，流域水文要素一致性遭受破坏，表征水文要素的特征值亦发生改变，水文频率重现期不再固定不变。时变矩方法主要分析水文频率曲线特征参数随时间变化的影响，如认为均值(m)和标准差(σ)随时间具有线性或抛物线性趋势特征，水文频率曲线可表示成含时间t的函数式，由此揭示水文特征值随时间的演变特征。

时变矩分析方法的具体计算思路是：首先进行水文序列一致性判断，若水文序列发生显著变异，则选择TVM方法进行分析。TVM分析时，选取合适的分布模型作为水文频率拟合线型，常用的分布模型有PIII分布、GEV分布、Gumbel分布等；选取合适的趋势模型(如线性或抛物线性趋势)嵌入分布模型，表征均值(m)和标准差(σ)随时间的变化特征；最后对分布模型进行参数估算和模型优选(本文选用极大似然法进行参数估计，采用AIC最小值法进行模型优选)，提出水文要素非一致性分析的最优拟合模型。具体计算流程见图2。

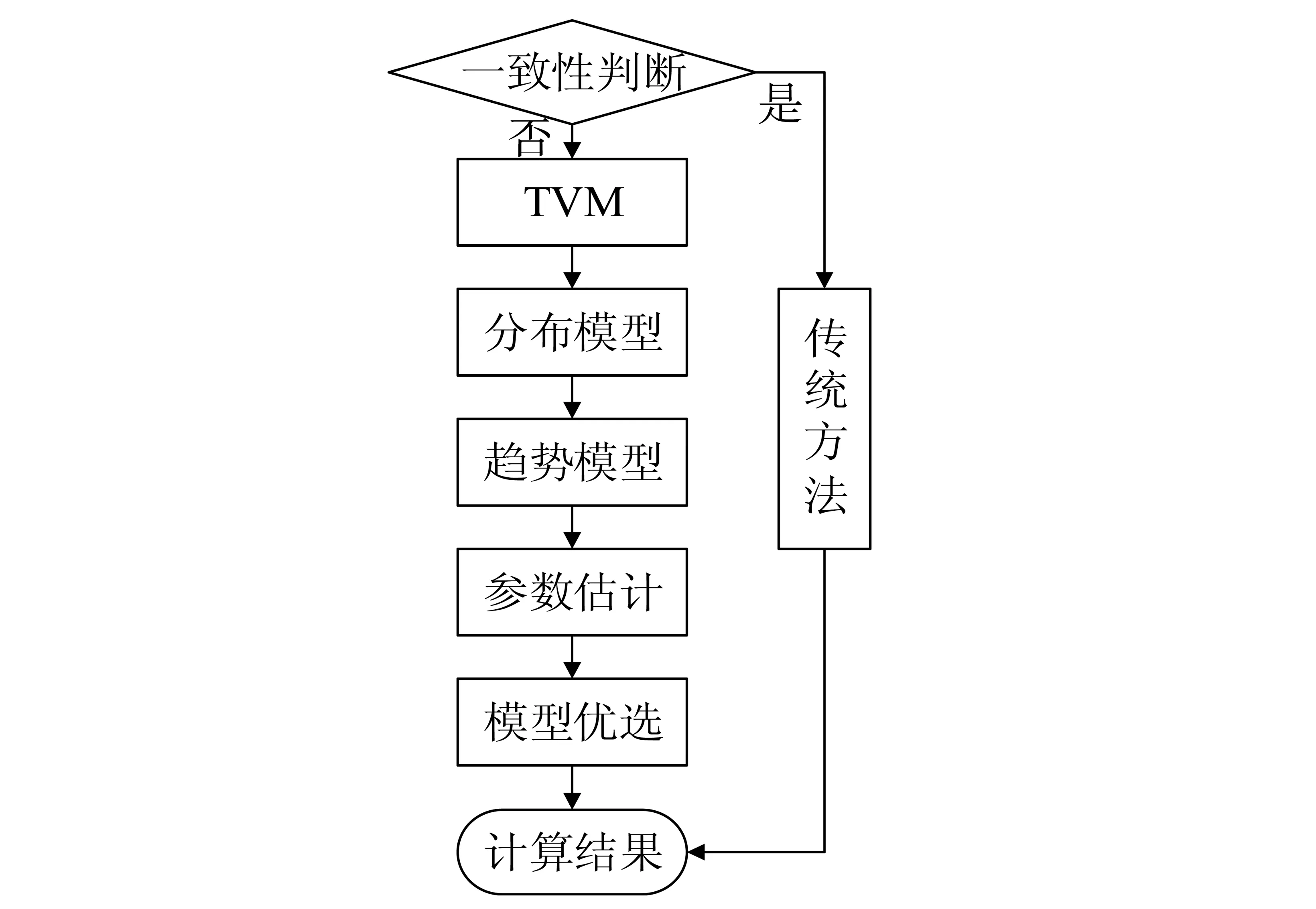
图2 TVM计算流程图Fig.2 The flow chart of TVM method

1)概率分布模型。为分析西北江三角洲地区洪水序列的水文频率适宜分布函数，选取了10种概率分布函数，其中二参数概率分布和三参数概率分布各5种。二参数概率分布包括Gamma分布、Gumbel分布、LN2(两参数对数正态分布)、Logistic分布和正态分布；三参数概率包括PIII分布、GEV分布[12]、GLO分布、Weibull分布[13]和LN3分布(三参数对数正态分布)。其中，三参数概率分布函数需分别选取一个参数作为不变值[14]，确定PIII分布和LN3分布不变参数为下界参数ξ，GEV分布、GLO分布、Weibull分布不变参数为形状参数k。

2)趋势模型。为分析均值(m)和标准差(σ)的时间变化特征，采用Strupczewski等[7]提出的TVM模型，考虑以下5种假设：均值具有趋势，记为A；标准差具有趋势，记为B；均值和标准差均具有趋势，且与固定Cv值相关，记为C；均值和标准差均具有趋势，两者无相关，记为D；均值和标准差均无趋势，记为O。对于均值和标准差具有的趋势，均可做线性趋势(L)和抛物线趋势(P)两种假设。各类概率分布模型均值和标准差趋势分类见表1。

3)参数估计。本次TVM模型选用极大似然法对概率密度函数进行参数估计，与传统极大似然法不同，TVM极大似然估计引入了时间t，表达式为：

(1)

式中，n为序列样本个数。

4)最优模型选择。本文选择AIC准则对最佳模型做出选择[15]，若AIC值最小，则模型最佳。AIC表达式为

AIC=-2lnML+2k

(2)

式中，ML为似然函数极大值；k为模型参数个数。

3 研究实例

3.1 水文序列一致性分析

受河道大规模挖沙等人类活动的影响，马口站和三水站的分流比发生显著变化，导致流量序列发生变异，序列一致性遭受破坏。选用1960-2009年马口和三水两个水文站逐年最大日流量序列进行非一致性水文频率分析，采用基于秩的非参数MK方法[16]进行趋势变异分析，结果表明：三水站与马口站的U值分别达到1.73和2.52，通过了置信度90%的显著性检验，表明马口站和三水站的年最大日流量序列趋势变异显著，符合TVM方法要求水文序列具有趋势变异的假设前提。

表1 各类趋势模型前两阶矩的表达式1)

3.2 TVM模型优选

在TVM模型中，选取10种水文分布模型和8种趋势模型进行组合，并选用极大似然估计法进行参数估计，采用AIC信息准则进行模型优选，结果见表2。按照AIC拟合值最小为原则，马口水文站年最大日流量序列最优拟合分布模型为GLO模型，最优拟合趋势模型为CP模型，TVM最优模型为GLOCP模型；三水站年最大日流量序列最优拟合分布模型为GEV模型，最优拟合趋势模型为AP模型，TVM最优模型为GEVAP模型。

3.3 计算结果分析

1)均值与标准差变化过程。分析马口站TVM法最优GLOCP模型和三水站TVM法最优GEVAP模型均值和标准差的变化过程，结果见图3。与传统的水文频率分析方法相比，发现近50 a来，马口站与三水站年最大日流量过程均值增幅分别达到20%和60%，马口站年最大日流量序列标准差也随时间呈抛物线型上升变化，增幅约为20%。

2)指定流量标准下重现期变化。选取指定流量为传统频率法T=100 a设计流量(马口站为52 550 m3/s，三水站为17 210 m3/s)，分析由TVM方法计算得到的指定流量标准(传统频率法T=100 a设计流量)下的重现期变化特征，结果见图4。结果表明，与传统频率分析下某一指定流量标准值重现期不变相比，TVM方法计算得到的指定流量标准值其重现期随着时间发生变化，马口站和三水站指定流量标准值的重现期呈抛物线型下降趋势：马口站指定设计流量下重现期从1960年150 a左右，增加至1975年达到最大接近200 a，1975年之后，重现期呈减少趋势，到2009年接近50 a。三水站指定设计流量下重现期从1980年以前大于600 a，1970年左右达到最大值约700 a，1970年之后重现期显著减小，至1990年重现期为200 a左右，1990年之后重现期减小速率放缓，至1995年之后重现期减小至100 a以下。此现象表明，同一设计洪水过程，在20世纪70年代属特大洪水(重现期较大)，而至2000年后降为一般洪水(重现期明显降低)。谢平等[17]在研究1960-2002年三水站年径流序列时，也发现三水站水文情势发生显著变化，包括指定设计流量的重现期明显变小等。

表2 TVM模型AIC拟合值

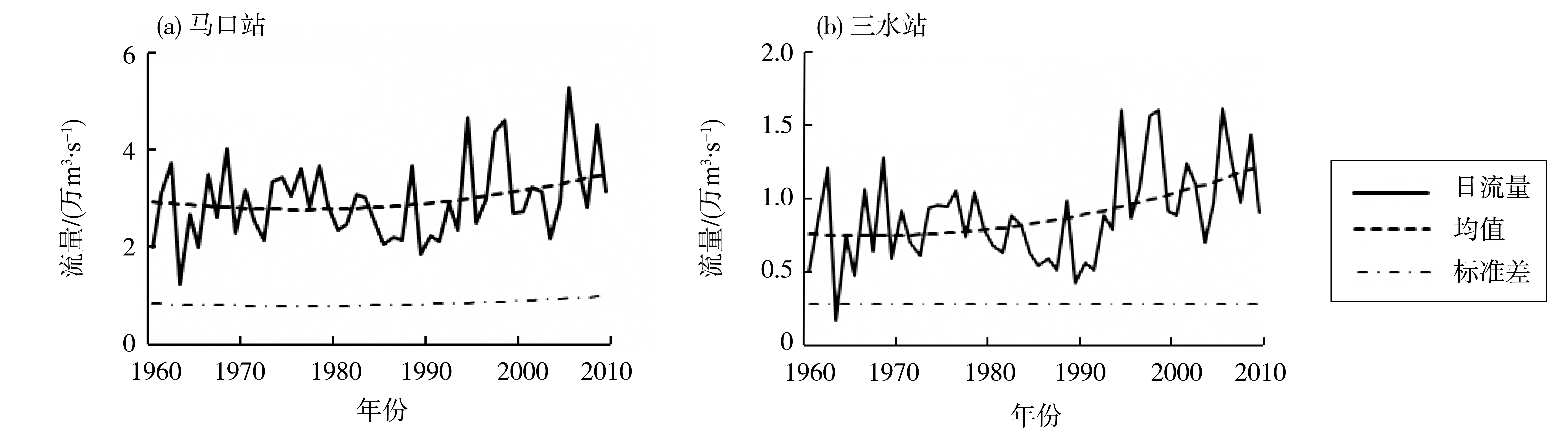
图3 TVM模型均值和标准差变化过程Fig.3 Changing process of the mean and standard deviation

3)指定重现期下设计流量变化。选取指定重现期T=100 a，分析由TVM方法计算得到该指定重现期标准下的设计流量变化特征，结果见图5。结果表明，与传统频率分析下某一指定重现期标准下的设计流量值不变(马口站52 550 m3/s，三水站17 210 m3/s)相比，TVM方法计算得到的指定重现期标准下的设计流量值随着时间发生变化：马口站和三水站指定重现期标准下的设计流量值呈抛物线型上升趋势。马口站指定重现期标准下的设计流量值从1960年56 000 m3/s左右减少至1975年52 000 m3/s左右，1975年之后呈增加趋势，到2009年67 000 m3/s左右，百年一遇标准下的设计流量值增大了20%。三水站指定重现期标准下的设计流量值呈现增加趋势且增加速率不断加快，从1960年15 000 m3/s左右增加至1990年16 000 m3/s左右，到2009年已接近20 000 m3/s，百年一遇标准下的设计流量值增大了30%。此现象表明，同一频率设计洪水，其流量值在20世纪70年代较小，至2000年之后明显增大。Zhang等[18]研究结果也表明随着水文序列的变异，西江与北江上中游地区的设计洪水值也发生了不同幅度的增长。

图5 指定重现期设计流量变化过程图Fig.5 Changing process of design discharge with the appointed return period

分析TVM方法计算得到的马口站和三水站洪水频率计算成果，两个水文站同量级洪水重现期均不断减小，大洪水出现频率不断增大，同频率洪水设计流量不断增大。根据西北江三角洲地区历史洪水事件，近年来该地区大洪水出现频率明显增大，同量级的洪水与历史相比大大增加，如90年代以来的西北江三角洲几场大洪水 “94.6”、“97.7”、“98.6”、“05.6”、“08.6”，在马口站和三水站洪峰流量均达到相当高的级别。可见，由TVM计算结果洪水频率和设计洪量的变化特点，与西北江三角洲近年来实际情况较为一致，TVM方法较好反应了不同时期环境变化对洪水频率和洪量的影响。

4 结 论

西北江三角洲河道挖沙剧烈影响下，西江、北江分流比明显发生变化，导致西江与北江流量过程一致性遭受严重破坏。本文选用TVM方法，选取1960-2009年西北江三角洲马口水文站和三水水文站共计50 a的年最大日流量数据序列，采用TVM方法，研究了西江和北江洪水频率非一致性问题。研究结果如下：

1)TVM方法通过考虑水文序列特征参数随时间变化的特征，能较好反映不同时期环境变化对洪水频率和洪量的影响，对于其余非一致性水文要素的频率分析和水利工程的设计标准的指导有启示意义。

2)与传统水文频率分析方法相比，TVM方法分析得到马口站和三水站指定流量标准下重现期越来越短，马口站在传统频率分析下百年一遇流量标准下的重现期缩短了2～3倍，三水站缩短了10倍以上；指定重现期标准下设计流量越来越大，百年一遇标准下马口站的设计流量值增大了20%，三水站增大了30%。这与近年来该地区大洪水出现频率增大的事实相一致。

TVM方法虽然在非一致性水文序列频率分析时具有一定的优势，但是该方法仍存在一定局限性，如该方法无法描述水文序列的跳跃式突变特征、利用时间函数描述非一致性将造成更大不确定性问题等。同时，TVM方法受样本容量限制影响较大，其结果的有效性尚待进一步论证研究。

[1] 蔡华阳,杨清书. 西北江网河来水来沙及分水分沙变化特征[J].热带地理, 2009, 29(5): 434-444.

[2] 张灵,王兆礼,陈晓宏. 西北江网河区顶端分流比变化特征研究[J].水文, 2010, 30(6): 2-4.

[3] 李新,曾杭,冯平. 洪水序列变异条件下的频率分析与计算[J].水力发电学报,2014(06):11-19，45.

[4] 宋松柏，李扬，蔡明科．具有跳跃变异的非一致分布水文序列频率计算方法[J]．水利学报，2012，43(6): 734-739,748.

[5] STRUPCZEWSKI W G, SINGH V P, FELUCH W. Non-stationary approach to at-site flood frequency modeling I: Maximum likelihood estimation [J]. Journal of Hydrology, 2001, 248: 123-142.

[6] KHALIQ M N, OUARDA T B M J, ONDO J C, et al. Frequency analysis of a sequence of dependent and/or non-stationary hydro-meteorological observations: A review [J]. Journal of Hydrology, 2006, 329: 534-552.

[7] STRUPCZEWSKI W G, SINGH V P, MITOSEK H T. Non-stationary approach to at-site flood frequency modeling III: Flood analysis of Polish rivers[J]. Journal of Hydrology, 2001, 248: 152-167.

[8] ICHARD M V, CHAD Y, MEGHAN W. Nonstationarity: Flood magnification and recurrence reduction factors in the United States [J]. Journal of the American Water Resources Association, 2011, 47 (3): 464-474.

[9] 叶长青,陈晓宏,张家鸣,等. 不同变化环境背景下非平稳性洪水频率对比研究[J]. 水力发电学报,2014(03):1-9，18.

[10] 杜涛, 熊立华, 江聪. 渭河流域降雨时间序列非一致性频率分析[J]. 干旱区地理, 2014, 37(3): 468-479.

[11] 刘德地,杜佩玲.不同条件下水文要素重现期的计算方法[J]. 水文,2014(5):1-5，74.

[12] 陈子燊,刘曾美,路剑飞. 广义极值分布参数估计方法的对比分析[J]. 中山大学学报(自然科学版),2010(6):105-109.

[13] 潘璀林,陈子燊. 基于GH Copula的韩江水文干旱联合概率分布研究[J]. 中山大学学报(自然科学版),2015(1):110-115.

[14] RAO A R, HAMED K H. Flood Frequency Analysis [M]. New York: CRC Press LCC, 2000.

[15] GUBER A K, PACHEPSKY Y A, YAKIREVICH A M, et al. Modeling runoff and microbial overland transport with KINEROS2/STWIR model: Accuracy and uncertainty as affected by source of infiltration parameters [J]. Journal of Hydrology, 2014, 519: 644-655.

[16] 于延胜,陈兴伟. 基于Mann-Kendall法的水文序列趋势成分比重研究[J].自然资源学报,2011(9):1585-1591.

[17] 谢平,唐亚松,陈广才,等. 西北江三角洲水文泥沙序列变异分析——以马口站和三水站为例[J].泥沙研究,2010(5):26-31.

[18] ZHANG Q, GU X H, SINGH V P, et al. Flood frequency analysis with consideration of hydrological alterations: Changing properties, causes and implications [J]. Journal of Hydrology, 2014, 519: 803-813.

Non-stationary flood frequency analysis of North River and West River Delta with time-varying moments

LIUBingjun1,QIUKaihua1,2,LIAOYeying1

(1.School of Geography and Planning, Sun Yat-sen University, Guangzhou 510275, China;2. Guangdong Water Resources and Hydropower Technology Promotion, Guangzhou 510150, China)

The time-varying moment (TVM) was used to analyze the non-stationary flood frequency in the North River and West River Delta and its response to the changing environment using the annual peak discharge records of Makou and Sanshui stations from 1960 to 2009. In comparison with traditional frequency analysis, TVM takes into consideration of varying characteristic parameters of hydrological time series and therefore gives better results reflecting the evolution character on the changing environment. The return period decreases with the appointed design discharges, while the design discharge increases significantly with the appointed return period, which is consistent with the phenomenon of more and more extreme hydrologic events in the North River and West River Delta in recent years.

North River and West River Delta; flood frequency analysis; non-stationary runoff series; time-varying moments

10.13471/j.cnki.acta.snus.2016.04.021

2015-09-01

广东省水利科技创新资助项目(2014-20)； 国家自然科学基金资助项目(91547108，50909106，91547202)

刘丙军(1976年生)，男；研究方向：水资源系统分析;E-mail:liubj@mail.sysu.edu.cn

TV122

A

0529-6579(2016)04-0130-06