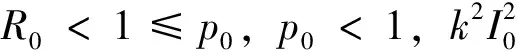具有密度依赖和有限抗病毒能力的计算机病毒模型的前向与后向分支*
李 君
(西安电子科技大学数学与统计学院,陕西 西安 710071)
具有密度依赖和有限抗病毒能力的计算机病毒模型的前向与后向分支*
李 君
(西安电子科技大学数学与统计学院,陕西 西安 710071)
研究了一个具有密度依赖和有限抗病毒能力的计算机病毒模型。首先分析了在阈值条件下系统平衡点的存在性和局部稳定性,然后给出了系统发生前向和后向分支的条件,同时证明了该系统的极限环是不存在的,并用数值模拟验证了结果。
抗病毒能力;稳定性;前向分支;后向分支
计算机病毒在网络上的传播和经典的传染病模型传播在许多方面都有非常类似的特征,因此其建模思想大致相同[1-8]。在大部分的传染病模型研究中,种群的总数量总是被假设为一个常数或者是满足指数增长的。但是由于网络资源的有限性,能够上网的计算机数量服从Logistic增长的密度依赖模式更符合实际,因此我们考虑在有限资源下的计算机病毒模型。
另一方面,杀毒软件是目前最有效的防治计算机病毒的方法之一[1,9]。正如文[1]中所述,杀毒软件的杀毒能力常与它的花费是成比例的。对于有限的软件花费,其杀毒能力也是有限的。因此我们采用下面的恢复函数
(1)

(2)
这里,A代表环境容纳量,即有限的网络资源所能承载的计算机的最大个数,k是指和已被感染电脑的联网时平均有效感染率,μ代表计算机由于老化等原因的自然淘汰比例,d是指由于病毒的影响使计算机瘫痪,从而退出网络的比例,函数T(I)是指杀毒软件的有效杀毒能力。记m=d+μ,由于方程组(2)的前两个方程不包含R(t),故只需要考虑下面的导出系统
(3)
1 正性和有界性
首先证明模型(3)的正性和有界性。
引理1 系统(3)具有初值S(0)>0,I(0)>0的所有解当t≥0时都是正的,且最终有界。
证明 显见直线S=0和I=0都是系统(3)的不变直线,因此区域
是系统(3)的正不变区域。下证所有的解S(t),I(t)在它们的存在区域里都是有界的。定义M=max{A,S(0)}。由于
故S(t)≤M对所有的t≥0都成立,即当t∈[0,∞)时S(t)存在且是有界的。记V(t)=S(t)+I(t),V(t)沿着系统(3)的正解的导数为
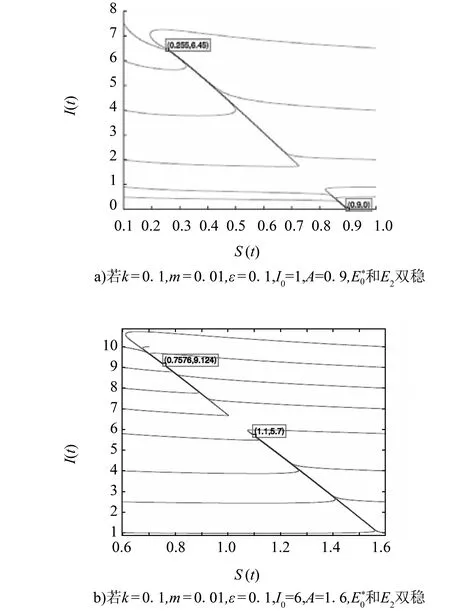
对于比较小的正常数0<τ 为得到系统的平衡点,令 (4) 以及 (5) (6) (7) 或者 (8) 因此b<0和Δ≥0当且仅当(7)式成立。假设(7)式成立,那么(6)式有两个正解I1与I2, 这里 (9) 相应地,记Si=A-kIi,Ei=(Si,Ii),i=1,2。 那么Ei是系统(3)的一个正平衡点当且仅当Ii>I0成立。若I1>I0,则 (10) 由b的定义可得, (11) 又由(10)式得 (12) 故当且仅当(11)式与(12)式成立时,有I1>I0。此外,当R0≤p1或者R0>p1,R0>p2,I1≤I0成立。类似地,若(11)式成立或者p2 峨眉健康文化思想是一种基于道教和佛教禅修的健康实践方法。“健康文化中的生命和长寿概念具有深刻的社会文化基础、强烈的精神和物质文化。”[13]与制度文化(人类为自己的生存和社会发展的需要积极创造的有组织的规范体系)形成对比,在峨眉武术健康文化的发展历程中,几千年来,在峨眉武术的各种拳种技术体系影响下,将古代中医保健思想融为一体,渗透儒、释、道思想,已成为一种宝贵的非物质文化遗产。但从精神文化(心理学概念和理论)的实证分析,峨眉武术健康文化被视为天、人、身、心的运动以及文武思想的延伸,成为健康文化的基本出发点和理论基础。 引理3 若R0 下面给出系统发生前向与后向分支的条件。由引理3中的(i)可得 定理1 假设R0≥p0, 在实际情况当中,(iv)和(v)所描述的情况是不同的。情形(iv)意味着当R0<1时计算机病毒将会持续,见图1。在情形(v)中,当R0>1时,系统不仅发生前向分支,而且还会发生后向分支,但当R0<1时计算机病毒将会被完全清除,见图2。前向分支图见图3,其参数值为k=0.1,m=0.01,ε=0.1,I0=12。 情形(iv)和情形(v)所发生的现象是非常有趣的,它们可以有效的帮助我们控制病毒的蔓延。事实上,从p0的表达式可以看出,当I0增加的时候p0也是增加的。当I0足够大,以至于p0>1,当R0<1时系统(3)不会发生后向分支。当继续增大I0直到R0 图1 若k=0.1,m=0.01,ε=0.1,I0=1,R0<1,病毒持续生存,后向分支Fig. 1 The virus is persistence and system occurs backward bifurcation if k=0.1,m=0.01,ε=0.1,I0=1,R0<1 图3 系统(3)的前向分支图Fig.3 The bifurcation diagram of system (3) 通过分析系统(3)在平衡点处的特征值,可以得到下面关于平衡点的局部稳定性的结论。 定理2 对于模型(3),下面的结论成立: (vii)E0是一个鞍点; (ix) 当1 (x) 当E1存在时它是一个鞍点; (xi) 当E2存在时它是一个稳定的焦点或结点。 定理3 如果下面的条件之一成立, (xii)R0<1,p0>1; (xiii)R0<1≤p1,p0<1; 下面证明原系统中不存在极限环。在大部分文献中,证明的方法是Dulac准则。这个准则是针对于光滑向量场的,但是系统(3)在I=I0处并不光滑,所以采用的是Wang[10]所采用的思想。记系统(3)的右端函数分别为f1和f2,则有下面的引理。 那么系统(3)不存在极限环。 证明 证明过程类似于文[10],略。 利用引理4,可以得到下面关于系统(3)极限环的不存在性。 定理4 系统(3)不存在极限环。 证明 由引理1的证明,若系统(3)存在极限环,那么它必存在于区域 考虑如下的函数B (13) 那么 对于I>I0, 故由引理4,系统(3)不存在极限环。 下面的定理给出了出现双稳情形的条件。 定理5 对于系统(3),下面的结论成立: (xv)如果max{1,p0,p1} 证明 情形(xv) 证明与上面类似,略。 图4 系统(3)出现的双稳现象Fig.4 The bistable of system (3) [1] REN J, YANG X, ZHU Q, et al. A novel computer virus model and its dynamics [J]. Nonlinear Anal Real World Appl, 2012, 13: 376-384. [2] YANG L, YANG X, WEN L, et al. A novel computer virus propagation model and its dynamics [J]. Int J Comput Math, 2012, 89: 2307-2314. [3] YANG L, YANG X. The spread of computer viruses under the influence of removable storage devices [J]. Appl Math Comput, 2012, 219: 3914-3922. [4] YANG L, YANG X, ZHU Q, et al. A computer virus model with graded cure rates [J]. Nonlinear Anal Real World Appl, 2013, 14: 414-422. [5] ZHU Q, YANG X, YANG L, et al. Optimal control of computer virus under a delayed model [J]. Appl Math Comput, 2012, 218: 11613-11619. [6] YANG L, YANG X. The impact of nonlinear infection rate on the spread of computer virus [J]. Nonlinear Dynamics, 2015,82: 85-95. [7] CHEN L, HATTAF K, SUN J. Optimal control of a delayed SLBS computer virus model [J]. Physical A, 2015, 427: 244-250. [8] MUROYA Y, KUNIYA T. Global stability of nonresident computer virus models [J]. Math Meth App Sci, 2015, 2: 281-295. [9] FORREST S, HOFMAYER S, SOMAYAJI A. Computer immunology [J]. Communications of the ACM, 1997, 40: 88-96. [10] WANG W. Backward bifurcation of an epidemic model with treatment [J]. Math Biosci, 2006, 201: 58-71. Forward and backward bifurcation of a computer virus model with density-dependent and limited anti-virus ability LIJun (School of Mathematics and Statistics, Xidian University, Xi’an 710071, China) A computer virus model with density-dependent and limited anti-virus ability is studied. The existence of equilibria is given and the local stability is established under the threshold value condition. After some mathematical analyses, it is showed that the forward and backward bifurcations occur and alsos proved that there is no limit cycle for system. Finally, the results are confirmed by numerical simulation. anti-virus ability; stability; forward bifurcation; backward bifurcation 10.13471/j.cnki.acta.snus.2016.01.006 2015-10-16 西安电子科技大学博士启动基金资助项目(7214614503);中央高校基本科研业务费资助项目(7215614501) 李君(1981年生),男;研究方向:常微分方程及其应用;E-mail:lijun@xidian.edu.cn O A 0529-6579(2016)01-0035-05
2 平衡点和稳定性分析


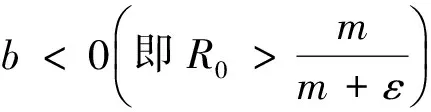
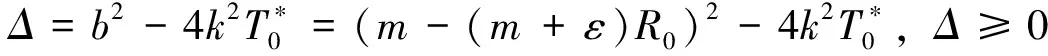





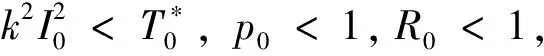




3 全局行为