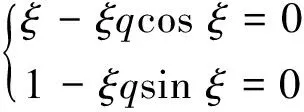Banach空间中立型泛函微分方程的概周期温和解*

张留伟

(中山大学中法核工程与技术学院, 广东 珠海 519082)

Banach空间中立型泛函微分方程的概周期温和解*

张留伟

(中山大学中法核工程与技术学院, 广东 珠海 519082)

借助于一般的谱分解技巧，利用线性算子半群理论研究了Banach空间X中立型泛函微分方程一致连续的有界温和解的存在性与唯一性，得到了当X没有与c0同构的子空间时方程概周期温和解存在与唯一的谱条件，推广了线性微分方程的现有结果。

概周期；Carleman谱；线性算子半群；中立型泛函微分方程

周期解与概周期解的存在性问题一直是微分方程研究的重要课题之一[1-2]，对于线性常微分方程而言，Massera于1950年证明了有界解的存在蕴涵周期解的存在。与周期系统不同，即便对于标量概周期常微分方程，所有解有界也未必蕴涵概周期解存在。因此，研究概周期微分方程概周期解的存在性时，除了假设解有界外还必须附加其他条件。一方面，对于概周期线性常微分方程而言，在附加了分离性的假设下，Favard首先证明了其概周期解的存在性，Kato建立了有限时滞概周期微分方程的分离性定理，袁荣[3]把Favard理论推广到逐段常变量微分方程。对于一般的Banach空间中的微分方程，Arendt[4]证明了在满足非齐次项Carleman谱可数的条件下一阶和二阶Cauchy问题概周期解的存在性。Batty[5]和Toshiki Naito[6]利用单调算子演化半群理论和Carleman谱分解技巧研究了Banach空间中周期演化方程

概周期解的存在性与唯一性。

本文研究抽象中立型时滞微分方程

(1)

概周期解的存在性，其中A是C0半群(T(t))t≥0的无穷小生成元，

r>0为一给定的实数，F:C([-r,0],X)→X是有界线性算子，且R(f)⊂D(A)，f是定义在上取值于Banach空间X的概周期函数。借助于一般的谱分解技巧，利用线性算子半群理论，得到了方程(1)概周期温和解存在与唯一的谱条件，推广了非齐次线性微分方程的有关结果并给出了所得结果的应用。

1 预备知识

令S1表示复平面中的单位圆。Rez表示复数z的实部。对给定的两个复Banach空间X，Y，L(X,Y)表示X到Y的所有有界线性算子所做成的Banach空间。σ(T)，ρ(T)，R(λ,T)分别表示算子T的谱，预解集和预解。BC(,X)，BUC(,X)分别表示X值有界连续函数空间和有界一致连续函数空间，并赋以范数‖x‖‖x(t)‖，则两者均为Banach空间。

对u∈BUC(,X)，记

引理1[7]设u∈BUC(,X)，则ξ∈SP(u)当且仅当u的Fourier-Carleman变换

在iξ的邻域无全纯扩张。

引理2[7-8]设f,gn∈BUC(,X)，当n→+∞时，gn→f，则

(i)SP(f)是闭的，

(ii)SP(f(·+h))=SP(f)，

(iii) 若α∈{0}，则SP(αf)=SP(f)，

(iv) 若∀n∈，SP(fn)⊂Λ，则SP(f)⊂，其中表示Λ的闭包，

(v) 若A是闭算子，∀t∈，f(t)∈D(A)，Af(·)∈BUC(,X)，则SP(Af)⊂SP(f)，

(vi) ∀ψ∈L1()，SP(ψ*f)⊂SP(f)∩supp(ψ)，

(vii) ∀ψ∈BC(,X)，SP(ψ+f)⊂SP(f)∪SP(ψ)。

引理3[5]A是Banach空间Y上C0等距群U=(U(t))t∈的无穷小生成元，z∈Y，ξ∈，存在中iξ的一个邻域V和全纯函数h:V→Y，使得h(λ)=R(λ,A)z，∀λ∈V，Reλ>0，则iξ∈ρ(Az)，其中Az是U限制在⊂Y上的无穷小生成元。

引理4[9]iSP(u)=Du，其中Du是(S(t))t∈限制在Muspan{S(t)u,t∈}上的无穷小生成元。

定义1 对ε>0，存在l(ε)>0 ，对∀a∈，∃τ∈(a,a+l)， 使得

则称ε>0是概周期函数。所有X值概周期函数记为AP(,X)，有AP(,X)⊂BUC(,X)。

设f∈AP(,X)，称使得

a(λ,f)

不为零的λ为f的Fourier指数，a(λ,f)为与λ相应的Fourier系数。f的所有Fourier系数的集合记为σb(f)，则σb(f)至多为可数集。

由文[5]知

定义2 连续函数u称为方程(1)的温和解，如果对所有t≥s，有

(2)

其中，(T(t))t≥0是以A为无穷小生成元的C0半群。

对u∈BUC(,X)，记u(r)Fur，易见是自治算子。记Thu(t)T(h)u(t-h)，则称Th为C0半群(T(t))t≥0的演化半群，其无穷小生成元记为G。

引理5 设(Th)h≥0是关于C0半群(T(t))t≥0的的演化半群，Q是BUC(,X)中所有(Th)h≥0的强连续点的集合，则

(i) 若u∈BUC(,X)是方程(1)的温和解，则u∈Q,

(ii) 设(Th)h≥0的无穷小生成G，有G(u+u)=Au-f，

(iii)AP(,X)⊂Q。

证明 (i) 由于u是方程(1)的温和解，有

由T(h)的强连续性，F的有界变差性， 及h，ω与t无关，知

即(Th)h≥0在u强连续。

(ii) 由于u是方程(1)的温和解，得

由线性算子半群的理论[10]，得知G(u+u)=Au-f。

(iii) 参见文[11]。

2 主要结论

本文的主要结论是定理1与定理2，在给出主要定理之前,先证明一些引理。

令

Δ(λ)λI-A+λBλ

引理6ρ(A,λ)是开的，Δ-1在ρ(A,λ)中解析。

证明 易见，∀λ，μ∈，有Δ(λ)-Δ(μ)∈L(X) ，且

因此，

由等式

知，μ∈ρ(A,λ)，故ρ(A,λ)在中是开的。

为证Δ-1的解析性，只须证Δ-1(λ)对∀λ∈ρ(A,λ)是可微的。设λ∈ρ(A,η)，取h∈，使得λ+h∈ρ(A,η)，注意到，当h→0时，

且

因此，当h→0 时，

引理7 设u∈BUC(,X)是方程(1)的温和解，则

(3)

证明 由u是方程(1)的温和解，知∀t∈，，且u(t)+Fut=u(0)+

即

对u进行拉普拉斯变换，得

记

则

显然，g(λ)在整个复平面上有全纯扩张。由于

为简便起见，记

M{v∈BUC(,X):σ(v)⊂S1∪S2)

其中S1，S2⊂S1是单位圆的两个不相交的闭子集。记Mv，有以下引理：

引理8[6]在上述假设下，有M=M1⊕M2，其中v∈Mi，当且仅当σ(v)⊂Si，i=1，2。

注1 对概周期函数仍有类似上述分解。

引理9 设u∈BUC(,X)是方程(1)的温和解，其中f∈AP(,X)，则SP(u)⊂SP(f)。

证明 由引理8知，若B是BUC(,X)上的自治算子，对u∈BUC(,X)，有SP(Bu)⊂SP(u)。由引理5及引理2，有

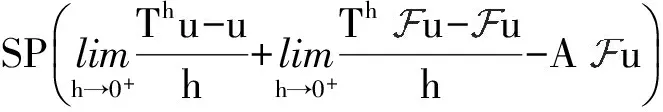
SP(u)

定理1 若

(4)

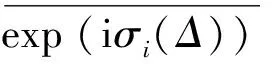
(5)

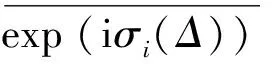
证明 有引理7，知SP(u)⊂σi(Δ)∪SP(f)，记Λ，令，由引理8，知存在投影P:M→M1，且P与，Th可交换。因此，

PG(u+

G(Pu+Pu)=APu-Pf

注意到Pf=f，知Pu也是方程(1)的温和解。

下证唯一性。 设v∈BUC(,X)是方程(1)的另一温和解，使得⊂，则ω-v是方程(1)对应齐次方程的解，因此，有SP(ω-v)⊂σi(Δ)。 注意到

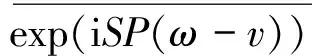
由文[12]及定理1，容易得到下述定理。

定理2 若

(6)

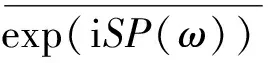
注2 当F=0 时，由本文的定理2 退化为文[6]中定理 3.5；而当F是一般的常差分算子时，我们给出所得结论的一个简单的应用。

例1 考虑中立型方程

(7)

其中,0

(8)

令λ=iξ，注意到exp(iξ)=cosξ+i sinξ， 代入(8)式，得

iξ+1-iξq(cosξ-i sinξ)=0

即

(9)

明显ξ≠0，由(9)式

(10)

[1]LIWG,LLIBREJ,WUH.Polynomialandlinearizednormalformsforalmostperiodicdifferentialsystems[J].DiscreteContinDynSyst, 2015, 36(1): 345-360.

[2]FIGUEROAP,PINTOM.Poincaré’sproblemintheclassofalmostperiodictypefunctions[J].BullBelgMathSocSimonStevin, 2015, 22 (2): 177-198.

[3]YUANR.OnFavard’stheorems[J].JDifferentialEquations, 2010, 249(8), 1884-1916.

[4]ARENDTW,BATTYCJK.Almostperiodicsolutionsoffirst-andsecond-orderCauchyproblems[J].JDifferentialEquations, 1997, 137: 363-383.

[5]BATTYCJK,HUTTERW,RBIGERF.AlmostperiodicofmildsolutionsofinhomogeneousperiodicCauchyproblems[J].JDifferentialEquations, 1999, 156: 309-327.

[6]NAITOT,MINHNV,SHINJS.Newspectralcriteriaforalmostperiodicsolutionsofevolutionequations[J].StudiaMath, 2001, 142: 97-111.

[7]NAITOT,MINHNV.Evolutionsemigroupsandspectralcriteriaforalmostperiodicsolutionsofperiodicevolutionequations[J].JDifferentialEquations, 1999, 152: 358-376.

[8]PRÜSSJ.Evolutionaryintegralequationsandapplications[M].Basel:Birkhäser, 1993.

[9]VUQP.AlmostperiodicsolutionsofVolterraequations[J].DifferentialIntegralEquations, 1994, 7: 1083-1093.

[10]DAVIESEB.One-parametersemigroups[M].London：AcademicPress, 1980.

[11]PAZYA.Semigroupsoflinearoperatorsandapplicationstopartialdifferentialequations[M].Berlin/NewYork:Springer-Verlag, 1983.

[12]LEVITANBM,ZHIKOVVV.Almostperiodicfunctionsanddifferentialequations[M].Moscow:MoscowUnivPublHouse, 1978 [EnglishtranslationbyCambridgeUnivPress, 1982].

[13]HINOY,NAITOT,MINHNV,etal.AlmostperiodicsolutionsofdifferentialequationsinBanachspaces[M].London/NewYork:Taylor&Francis, 2002.

Almost periodic mild solutions to functional differential equations of neutral type in Banach space

ZHANGLiuwei

(Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai 519082, China)

With the general spectral decomposition techniques and by means of the linear operator semigroups theory, the existence and uniqueness of uniformly continuous mild solutions to the functional differential equations of neutral type in Banach spaceXarestudied.ThespectrumconditionswhichimplytheexistenceanduniquenessofalmostperiodicmildsolutionstotheequationsareobtainedwhenXhasnosubspaceisomorphictoc0.Theresultsextendrecentresultsofthelineardifferentialequations.

almost periodicity; Carleman spectrum; linear operator semigroups; functional differential equations of neutral type

10.13471/j.cnki.acta.snus.2016.01.005

2015-09-14

国家自然科学基金资助项目(11271379)

张留伟(1982年生)，男；研究方向：泛函微分方程;E-mail:zhliuw@mail.sysu.edu.cn

O

A

0529-6579(2016)01-0030-05