关于线性代数教学的几点思考

朱艳丽（华南农业大学　数学与信息学院，广东　广州　510642）

关于线性代数教学的几点思考

朱艳丽
（华南农业大学数学与信息学院，广东广州510642）

摘要：随着信息技术的飞速发展，线性代数在许多科学领域起着越来越重要的作用，线性代数也成为高等院校的一门重要的基础课程，本文主要介绍了两点在线性代数教学中学生经常遇到的问题以及解决的方法，这在教师的实际教学和学生日常学习中非常实用，最后也对如何学好这门课提出了一些自己的建议。

关键词：特征值；可逆；正交；正定；对称

引言

线性代数是高等院校的一门重要基础课程，随着计算机科学的飞速发展，使它在许多科学领域都起着越来越重要的作用。由于线性代数里面所包含的基本概念较多，涉及的理论和方法具有较强的逻辑性和抽象性，以至于很多学生，尤其中学是文科背景出来的学生学习起来非常吃力。本文主要介绍两个在线性代数学习中学生容易遇到的问题和解决的方法，第一个是学生在求矩阵特征值时经常遇见的问题，一旦遇到矩阵特征方程的次数是三次或三次以上时，学生往往不知道如何分解因式求特征值，针对这个问题通过代数学里的艾森斯坦判别法来解决；第二个是对于书本里面四个容易混淆的概念：可逆矩阵、正交矩阵、正定矩阵、对称矩阵的定义进行了梳理，并讨论了它们之间的区别和联系，让大家对这四个概念有着更加清晰和深刻；最后对如何学好线性代数提出了一些建议。

一、用艾森斯坦判别法求矩阵的特征值

在线性代数的学习中，求矩阵的特征值经常遇到，因为这在矩阵的对角化和二次型化标准形时都要用到。而求矩阵的特征值需要先求矩阵的特征多项式，再求特征多项式的根。这时一旦遇到次数是三次或三次以上的特征多项式求特征根时，学生往往不知道怎么分解因式找特征根，这时可以使用代数学里的艾森斯坦判别法来解决。下面先介绍艾森斯坦判别法的定理内容：定理：f(x)=anxn+an-1xn-1+…+a0是一个整系数多项式，而是它的一个有理根。其中r,s互素，那么必有s|an,r|a0。特别的，如果f(x)的首项系数an=1，那么f(x)的有理根都是整数，而且是a0的因子。

1.如果矩阵的特征多项式是整系数多项式，由于特征多项式的首项系数为1，使用艾森斯坦判别法我们知道矩阵的特征值一定是其特征多项式中常数项的因子，这样求特征值的范围就大大缩小了，可以先找出特征多项式中常数项的所有因子，它们就是矩阵的所有可能的特征值，最后再把它们带回到特征多项式中，满足该特征方程的就是矩阵的特征值。下面我们看一道例题：

解：矩阵A的特征多项式为：f(λ)=|λI-A|=λ3-6λ2+3λ+10，由艾森斯坦判别法可知该矩阵的特征值是常数项10的因子，所以可能的特征值有±1,±2，±5,±10代入特征多项式后发现-1,2,5是矩阵A的特征值。

2.如果矩阵的特征多项式是有理系数但不是整系数多项式时，我们可以找到一个与之有相同特征值的整系数多项式，从而也可以使用艾森斯坦判别法求出其特征值。如例2：

这个方法在求特征值时非常有用，尤其是对次数是三次以及三次以上的特征多项式求有理特征根时效果明显，并且简单，容易操作，学生很容易理解和掌握，在日常的教学中可以介绍给学生。

二、可逆矩阵、正交矩阵、正定矩阵、对称矩阵的区别与联系

线性代数这门课程逻辑性强，前后知识点联系紧密，理解清楚每个概念非常重要，由于涉及到的概念较多，学生对概念理解的不够彻底，容易把很多概念混在一起。最常见的问题是学完整本书后，把矩阵里面的可逆矩阵，正交矩阵、正定矩阵、对称矩阵混在一起，搞不清楚它们之间的区别和联系因此有必要把这几个概念理清楚。可逆矩阵的概念在线性代数的学习里经常见到，它几乎贯穿在整个线性代数的学习中，可逆矩阵一般可以用三种方式来定义：1. n阶矩阵A可逆当且仅当存在n阶矩阵B使得AB=(BA)=I（I为单位矩阵）；2. n阶矩阵A可逆当且仅当存在有限个初等矩阵p1,p2,…，pn使得A=p1,p2,…，pn；3. n阶矩阵A可逆当且仅当（A*为A的伴随矩阵）。

第一个是可逆矩阵最基本的定义，是后面两个定义的基础，在有关可逆矩阵的证明时会常用到；第二个定义是用初等变换求逆矩阵的基本原理，在实际的求逆矩阵时我们经常会使用初等变换求矩阵的逆矩阵；第三个定义在实际操作中经常用来判断矩阵是否可逆，因为只需要判断矩阵的行列式是否为零就可以了，方法简单容易操作。正交矩阵的定义有两种：1. n阶矩阵A为正交矩阵当且仅当AAT=ATA=I；2. n阶矩阵A为正交矩阵当且仅当矩阵A的行向量和列向量都是标准正交向量组。

第一个定义是正交矩阵的基本定义，在许多关于正交矩阵的证明里会用到；第二个定义可以从矩阵本身看出其是否为正交矩阵，在实际的判断正交矩阵时经常用到。

正定矩阵是根据二次型来定义的，它的定义是通过正定二次型来刻画的，正定二次型对应的对称矩阵称为正定矩阵，所以正定矩阵首先是对称矩阵。关于正定矩阵的等价命题一般常用的有三种：

1.实对称矩阵A正定当且仅当A与单位矩阵I合同；2.实对称矩阵A正定当且仅当存在可逆矩阵C使得A=CTC；3.（霍尔维茨定理）实对称矩阵A正定当且仅当A的所有顺序阶主子式均大于零。

其中在证明与正定矩阵有关的问题时经常用到前面两个命题，而最后一个命题是我们在实际中判断一个矩阵是否正定最常用的方法。

对称矩阵的定义一般有两种：1. A为对称矩阵当且仅当AT=A；2. A=(aij)为对称矩阵当且仅当aij=aji，即矩阵A关于主对角线对称位置上的元素对应相等。

第一个定义是对称矩阵的基本定义，在许多关于对称的证明里会用到；第二个是从矩阵的元素来定义它的对称性，非常的直观且容易理解。

通过对定义的分析和理解，可以很容易分清四者的区别和联系：1.正交矩阵，正定矩阵都是可逆的，因为正交矩阵的行列式为±1，正定矩阵的行列式大于零，都不等于零，所以可逆；2.正交矩阵和正定矩阵之间没有特别的联系，但正定矩阵一定是对称矩阵，正交矩阵不一定是对称矩阵；3.有限个可逆矩阵相乘还是可逆的，有限个正交矩阵相乘也是正交的，但是两个正定矩阵相乘未必正定，两个对称矩阵相乘也未必是对称矩阵；

其实如果n阶矩阵A,B均为对称矩阵，AB为对称矩阵当且仅当AB=BA，由于矩阵的乘法一般不满足交换律，所以两个对称矩阵相乘未必是对称矩阵。

4.在平时的教学中，很多学生会问，矩阵的可逆性，正交性，正定性，对称性对矩阵的加法和减法保持吗？即A,B可逆，A±B可逆吗？当然不一定，这些反例证明是很容易的。

三、结束语

在线性代数的教学和学习中，无论是求矩阵的特征值还是关于可逆矩阵、正交矩阵、正定矩阵，对称矩阵、它们都是非常基础和重要的知识点，在线性代数教学中经常遇到，这样的解释和总结往往让学生更容易理解和掌握，可以在平时的教学中使用。学好线性代数首先要做到：1.理解清楚定义，这是最基本的第一步，只有对每个概念的定义理解清楚了，才能开始下一步的学习；2.会用基本定理，对于有的定理而言，证明的过程不需要掌握，但是要知道该定理用在什么地方以及怎么用；3.掌握常用方法，比如求逆矩阵的方法，求行列式的方法，判断线性方程组是否有解，以及如何求出解的方法，化二次型为标准形的方法等等；4.善于总结归纳，把一些容易混淆的定义放在一起，找出它们之间的区别和联系，比如：矩阵与行列式，初学线性代数的人会经常搞不清楚它们的关系，本质的区别就是，矩阵是一张数表，行列式是一个具体的数值；形状上看，矩阵的行数和列数不一定一样，行列式的行数和列数必须一样；写法上来看，矩阵一般用大写的小括号表示，行列式一般用两条竖线表示；它们之间的联系就是只有方阵才可以求它的行列式。5.通过找反例解决心中疑问，比如：行列式有乘法规则，即A,B是数域P上的两个n阶矩阵，那么|AB|=|A||B|，这时有同学就会提出问题，|A+b|=|A|+|| B||是否成立？这时可以通过找反例解决这个问题，如令A=

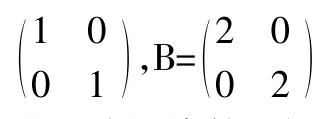
，则|A+B|=9≠5=1+4=|A|+|B|。以上就是对如何学习线性代数这门课提出的一些建议，相信只要做到以上几点，一定可以学好这门课。

参考文献

[1]北京大学数学系几何与代数教研室前代数小组.高等代数（第三版）[M].北京：高等教育出版社，2003.

[2]盛骤，谢式千，于渤.线性代数[M].北京：高等教育出版社，2012.

[3]魏福义，黄燕萍.线性代数[M].北京：中国农业出版社，2012.

[4]同济大学数学系.线性代数（第五版）[M].北京：高等教育出版社，2007.

Abstract:With the rapid development of information technology, linear algebra plays an increasingly important role in many scientific fields; it is an important basic course in higher education. This paper mainly introduces the problems and solutions which are often encountered in linear algebra teaching, finally also putting forward some suggestions on how to learn this course.

Keywords:eigenvalue; reversible; orthogonal; positive definite; symmetric

中图分类号：G642

文献标志码：A

文章编号：2096-000X（2016）05-0132-02

作者简介：朱艳丽（1979-），女，汉族，四川眉山人，硕士，讲师，研究方向：代数图论，组合图论。