利用激光扫描点云的碳纤维织物表面三维模型重建

程 杰， 陈 利

(1. 天津工业大学 信息化中心， 天津 300387； 2. 天津工业大学 纺织学院， 天津 300387)

利用激光扫描点云的碳纤维织物表面三维模型重建

程 杰1， 陈 利2

(1. 天津工业大学 信息化中心， 天津 300387； 2. 天津工业大学 纺织学院， 天津 300387)

织物表面的自动化分析与测量是纺织企业需要解决的重要问题。针对该问题，利用三维激光扫描系统，运用调整照明、分析织物组织循环图和控制扫描范围的方法采集到高质量、密集的碳纤维织物表面原始点云。对原始点云实施了分类预处理。通过向预处理后的点集中加入点云约束条件和梯度约束条件构建了尺度独立的屏蔽约束条件，重建出较为理想的碳纤维织物表面三维模型。结果表明，利用重建模型测量纱线宽度的平均测量误差为0.12 mm。

碳纤维织物； 三维激光扫描； 滤波降噪； 三维重建

碳纤维织物具有膨胀系数低、强度和模量高等卓越的物理和力学性能，在工业上应用广泛。碳纤维织物表面结构分析与结构参数表征是复合工艺和微观力学设计的重要基础，也是纺织企业生产的重要依据。传统上，这个工作是由技术人员借助照布镜等仪器手工完成，分析过程费时，效率很低。数字图像处理技术是20世纪80年代提出的织物表面分析最为简便有效的方法。利用这种方法，对普通面料的经纬密度、花节长度等参数进行了测量并取得了较为理想的结果。该技术直接利用表面灰度变化，或将灰度信息转换到频率域处理。这就意味着环境光、背景光等照明条件将直接对图像质量产生极大影响。

三维采集技术借助仪器和算法获取物体表面三维坐标，拓展了观察和分析的视角。在诸多三维信息采集方法中，三维激光扫描技术能够在短时间内获得密集的空间点云，并具有测量精度高，采样不受曲面复杂度影响、能够在一定程度上克服周围光线条件和采样样品光学条件影响等优势。作为一种高效精确的非接触式测量方法，已经被应用到文物保护、雕塑制作等工程领域。

在纺织行业中，三维技术已被应用于织物表面三维模型的构建与相关检测中。沈毅等[1]利用平行结构光和基于极坐标径向扫描的方法对织物投影图像中等高线条纹及织物边缘进行识别，得到织物曲面上的等高线及织物边缘点坐标，最后利用基于极坐标网格的三维曲面建模方法对悬垂织物的三维形态进行了重建。刘瑞鑫[2]借助光度立体视觉方法，在梯度空间矢量中恢复了织物表面的高度信息。Kang等[3]利用电荷耦合元件双CCD和激光投影的立体视觉方法重建了起球的织物表面，并利用高度阈值算法将分层接结的三维表面模型转化为二进制图像后提取了相关参数，进而完成了表面起球评级。Ouyang等[4]利用织物表面的深度信息检测了织物起球程度，并提取出织物密度等参数。目前，三维激光扫描所获得的密集散乱点云还主要用于人体模型等较大模型的构建[5]与分析中。

本文采用三维激光采集与处理技术，获得了理想的织物点云。在此基础上，重建了较为精确的织物表面三维模型，为后续表面结构分析与参数表征提供精确的三维数字化模型，进而有利于提高分析测量的自动化程度。

1 碳纤维织物表面三维点云的采集

碳纤维织物表面原始三维点云采用海科斯康公司旗下的柔性关节臂ROMER配合Scan Shark V4ix激光扫描测头所组合成的三维激光扫描系统扫描完成。该设备每秒扫描23 000个点，扫描精度为24 μm。利用30 Hz的红色激光线对织物一侧表面反复扫描，扫描距离为15 cm。扫描设备控制端软件采用该公司旗下产品SCANWORKS。扫描样品为12 K碳纤维平纹机织物与斜纹机织物，如图1所示。

图1 碳纤维织物样品Fig.1 Carbon-fiber fabric sample. (a) Plain; (b) Twill

一般情况下，三维激光扫描技术能够迅速采集到百万级的原始点云。然而，碳纤维织物表面全黑且反光率极高。对于高反光率表面，喷涂是常用的方法，但喷涂显然是破坏面料的做法，于自动化生产不利。为此，本文将碳纤维织物平铺于实验台上，利用低照度环形灯对实验台扫描面积作均匀照明，克服了这一问题。实验系统的建立如图2所示。

图2 实验系统建立Fig.2 Set-up of experimental table

为简化数据，根据实验目的合理选择扫描范围十分必要。由于后期织物表面结构参数测量所选视野范围至少应当包含2×2个完全组织循环，而所选取的平纹和斜纹碳纤维织物样品的纱线循环数分别为2和8，因此扫描范围应当至少分别达到10 mm×10 mm和54 mm×54 mm。如果考虑到织物经纬密度的测量是判断10 cm之内经向和纬向纱线根数，为防止边界扫描点云数据点不足，在扫描时可适当增加扫描范围。为此，采集过程中分别对平纹和斜纹织物10 cm×10 cm和15 cm×15 cm左右的正方形范围内的织物一面进行了反复扫描。取样，为避免由于切割或拉伸引起织物边缘形变，扫描区域为大块碳布的中部，扫描时尽量保持面料表面平整，使织物紧密贴合在实验台上。

经过反复扫描,获得平纹织物表面原始点云1 432 846个，斜纹织物1 919 669个。在原始点云的可视化效果中，纱线走向可分辨，但放大后细节不清晰，且存在大量噪声和孔洞，这是设备在设计原理及精度上存在缺陷、测试环境中存在不可避免的干扰、操作中的人为误差和被测表面的物理属性影响[6]等因素导致的。

在实践中，直接利用原始扫描点云重建碳纤维织物表面模型(如泊松重建)仍然存在很多困难[7]。比如碳纤维织物表面纹理起伏十分微小，对噪声更为敏感，重建模型上会形成更多的假面，根本无法取得精确的三维重建模型,更无法完成后续的基本测量。以斜纹织物样品为例，图3、4分别示出渲染后的原始扫描点云效果和利用原始点云重建出的织物表面。

图3 渲染后的斜纹织物原始扫描点云效果Fig.3 Rendered visualization of original points cloud of twill

图4 利用原始扫描点云重建出的斜纹织物表面Fig.4 Reconstruction of original scanning points cloud of twill

2 织物表面原始点云降噪

为尽量避免噪声和空洞的干扰，本文在重建织物表面形态之前对不同分布特征的原始点云进行分类处理。

2.1 离群点的剔除

离群点远离整体点云，对刻划表面特征无用，应当剔除。Ramaswamy等[8]提出将离群点看作k邻域中与对象距离最大的前n个点。这一方法不对离群点作排序或评级，但是需要首先给定参数。为找到一种自动化程度更高、能够最大限度排除预设参数对结果影响的方法，陆声链等[9]提出了基于距离之和的离群点检测，算法首先要确定用户期望得到的离群点数量M，然后计算数据集中两两对象之间的距离并累加，距离之和最大的M个对象被判断为离群点。

实验中，数据点最近邻域的数量设为k=50，平纹和斜纹织物原始点云中离群点平均去除率为1.89%。

利用去除离群点后的散乱点云需要转换为三角网格模型文件进行下一步处理。

2.2 内点位置的调整

内点与真实点数据混杂在一起，在测量允许的误差范围内，经过一定的处理可用于描述织物表面特征。本文实验将调整这部分噪点的位置，使其尽量回归织物表面。

经典的Laplacian算子利用网格顶点邻域位置的平均值迭代式的校正有限元网格的顶点位置，但是，调整过程会导致模型出现明显的变形与体积收缩。为此，Taubin[10]、Vollmer等[11]、Desbrun等[12]对Laplacian平滑进行了改进。其中，Taubin的λ/μ方法利用两级转换函数，以不同尺度因子连续2次对网格模型做Laplacian平滑。该方法平滑速度适中，特征保持与增强性能卓越，经过大量实验，与其他几种Laplacian改进算法[10-12]和双边滤波算法[13]相比，最适合于碳纤维织物表面三维网格处理。

假设，离散表面信号是一个定义在多面体表面顶点上的函数x={x1,…，xn}t。那么，这个离散的表面信号的Laplacian算子可用邻域的权重均值表示为

(1)

式中wij为权重且为非负值，且有

(2)

△x=-Kx

(3)

本文K是对称循环矩阵：

高斯滤波和尺度空间理论是参数曲面中基于卷积的平滑算法中最常用的方法。应用这2种方法，平滑算法用矩阵可表示为

x=x+λ△x=(1-λk)(1-μk)x=f(K)x

(4)

式中：尺度因子0<λ<1，μ<-λ<0，用于控制扩散速度k∈[0,2]。f(K)是通过评价矩阵K中的单边多项式f(K)=(1-λk)(1-μk)获得的矩阵。对于N次迭代过程，则有

f(k)=(1-λk)(1-μk)N/2(N为偶数)

大量实验表明：参数取λ=0.3,μ=-0.43，迭代9次时的平滑与特征保持效果最好，如图5所示。

3 碳纤维织物表面三维重建

预处理后的点云去除了距离表面很远的离群点，表面特征得到了增强。然而，要从这些包含了实体模型几何形状的散乱点云数据中构建织物表面三维形态就需要推断未知表面的拓扑结构，精确地拟合含有噪声的数据，并且合理地填充空洞,这个过程就是表面三维重建过程[14-16]。

表面三维重建就是要得到曲面的近似数字化表征，包括插值和拟合2种方法。插值方法是将表面所有或者大部分集中的数据点作为初始条件，通过内插获得密集的三角面片，并将这个三角面片的集合作为表面模型。很显然，如果噪声集中，重建表面就会偏离实际表面，因此还要依靠后续的修正和平滑处理获得理想表面。拟合方法利用采样点云直接重建近似表面，根据曲面表征形式的不同，可分为显示拟合(显式表面重建)和隐式拟合(隐式表面重建)。显式拟合将二维参数变换到三维空间，算法成熟，擅长拟合单一曲面，但在处理过渡曲面和分块拟合复杂曲面时依赖大量的人工分割、拼合操作。隐式拟合利用等值面进行表面重建。在处理过渡曲面、保持曲面完整性和光顺性方面非常有优势，但许多算法仍然处于研究阶段，实际应用不多，是三维技术领域研究的热点[17]。

3.1 重建原理

泊松重建[11]是一次性拟合所有数据点的隐式重建算法。与其他重建方法相比，不易形成伪平面，在求解时又可形成一个良性的线性系统。

(5)

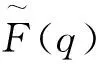
(6)

由此，泊松表面重建的核心可表达为通过精确估计模型的指示函数和提取等值面去无限逼近真实的表面模型。

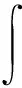
(7)

利用Euler-Lagrange方程，用梯度的散度(标量函数的拉普拉斯算子)代替梯度。平滑后指示函数梯度的散度与模型内表面向量场散度之间的关系可表示为标准的泊松方程形式，如式(8)。

(8)

尽管泊松重建是从三维扫描点云中重建出水密表面的有效算法[15]，然而它仅利用一个全局性的偏移量校正指示函数。在实际中，选取一个最为合适的全局偏移量是非常困难的。为此，可利用显式插值的方法[12]提高模型的精确度。

向式(7)增加适当约束条件修正采样点误差，如式(9)所示：

(9)

式中：α为衡量拟合梯度和拟合值重要性的权重；Area(S)通过计算局部采样密度获得的重建表面面积，取w(p)=1。式(9)可被简化为

(10)

本文，〈·,·〉(w,P)是单元立方体函数空间的双线性、对称、为正、半定义的表达形式，该表达式通过函数值的权重和获得，如式(11)。

(11)

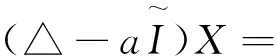
(12)

式中，△表示拉普拉斯算符。屏蔽泊松方程利用瀑布式多重网格解法求解。

等值面的提取借助经典的步进立方体算法[18]完成。理想情况下，采样点应当位于指示函数的零值表面上。然而由于采样噪声、八叉数构建采用了近似值等原因，等值面绝非零值面。一般取采样点指标函数值的加权平均作为标准值γ。

(12)

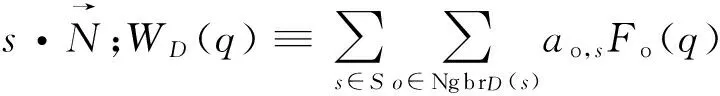
3.2 重建实验

运用屏蔽泊松方法重建织物表面时，以去除离群点并利用Taubin的λ/μ方法滤波(λ=0.3,μ=-0.43，迭代9次)后的点集作为输入点集，分别在八叉树深度为6至12下分别利用泊松重建和屏蔽泊松算法重建了织物表面。结果表明，深度为11、12时的重建效果明显好于深度小于10时的重建效果，但深度为11和12时的重建效果之间差别并不大。而当重建深度增加1，重建时间将增加50%～100%。为同时兼顾重建效果和运行效率，八叉树深度为11时，重建效果就能够满足后期分析要求，而不必为追求更完善的细节过多增加运行时间。经过渲染后的重建效果如图6所示。

图6 八叉树深度为11时平纹织物和斜纹织物的重建效果 Fig.6 Rendered visualization of 3-D surface models of plain (a) and twill (b) at octree depths 11

重建出来的碳纤维织物表面的三维模型可作为后续测量的基础模型。

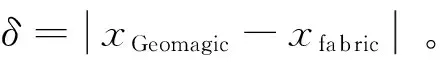
实验中，直接拾取三维重建表面模型两点距离得到平纹织物经纱宽度为2.896mm，纬纱为2.911mm；斜纹织物经纱宽度为2.903mm，纬纱为2.947mm；人工直接测量布样时得到平纹织物经纱宽度为3.02mm，纬纱为3.04mm；斜纹织物经纱宽度为3.03mm，纬纱为3.04mm。由此可知，在重建模型上，经纱宽度的平均测量误差为0.13mm，纬纱宽度的平均测量误差为0.11mm。

4 结 论

本文利用柔性关节臂+线激光扫描头所组成的三维扫描系统采集到了织物表面原始点云。对织物表面原始点云实施了分类预处理。利用基于邻域点欧式距离的平均值作为测度剔除了1.895%的离群点。在此基础上，应用Taubin的λ/μ算法对织物点云进行平滑处理，调整了点云中的第2类噪声(内点)。当λ=0.3,μ=-0.43，迭代9次时的处理效果最佳。最后，通过向重建输入点集能量公式中加入点云约束条件和梯度约束条件构建了尺度独立的屏蔽约束条件。当重建深度取11时，在兼顾运行效率的同时，重建出了理想的碳纤维织物表面三维模型。结果表明，利用重建模型测量相比于直接利用面料所得的纱线宽度的平均测量误差为0.12mm。由于该模型包含了边缘上任意一点的三维坐标信息，因此可用于后续的织物表面形态与纹理分析，还可作为相关参数自动化测量的基础模型。基于该模型的测量是利用空间坐标而非表面光线特征，从而能够一定程度上克服光线条件给测量带来的不良影响。

[1] 沈毅, 刘玄木, 王寿兵. 织物悬垂三维形态的测量与重建[J]. 纺织学报, 2006, 27(6): 12-15.SHENYi,LIUXuanmu,WANGShoubing.Measurementandreconstructionof3Ddrapingshapeofwovenfabric[J].JournalofTextileResearch, 2006, 6(6): 12-15.

[2] 刘瑞鑫. 织物褶裥等级客观评估系统的研究[D]. 南京：东南大学, 2012: 12-16.LIURuixin.Studyonobjectiveassessmentsystemoffabricpleatgrade[D].Nanjing:SoutheastUniversity, 2012: 12-16.

[3]KANGTJ,CHODH,KIMSM.Objectiveevaluationoffabricpillingusingstereovision[J].TextileResearchJournal, 2004, 74(11): 1013-1017.

[4]OUYANGW,WANGR,XUB.Fabricpillingmeasurementusingthree-dimensionalimage[J].JournalofElectronicImaging, 2013 (22): 9-13.

[5] 黄海峤，莫碧贤，郭绮莲, 等. 从三维人体扫描生成服装样板[J]. 纺织学报, 2010, 31(9): 132-142.HUANGHaiqiao,MOBixian,GUOQilian,etal.Garmentpatternsgeneratingbasedon3-Dbodyscann-ing[J].JournalofTextileResearch, 2010, 31(9): 132-142.

[6] 李宝, 程志全, 党岗, 等. 三维点云法向量估计综述[J]. 计算机工程与应用, 2010, 46(23): 1-7.LIBao,CHENGZhiquan,DANGGang,etal.Surveyonnormalestimationfor3Dpointclouds[J].ComputerEngineeringandApplication, 2010, 46(23): 1-7.

[7]LIMSP,HARONH.Surfacereconstructiontechniques:areview[J].ArtificialIntelligenceReview, 2014(42): 59-78.

[8]RAMASWAMYS,RASTOGIR,SHIMK.Efficientalgorithmsforminingoutliersfromlargedatasets[C]//.ACMSIGMODRecord.ACM, 2000: 427-438.

[9] 陆声链, 林士敏. 基于距离的孤立点检测研究[J]. 计算机工程与应用, 2004(33): 73-94.LUShenglian,LINShimin.Researchofdistance-basedoutliersdetection[J].ComputerEngineeringandApplication, 2004(33): 73-94.

[10]TAUBING.Asignalprocessingapproachtofairsurfacedesign[C].//Proceedingsofthe22ndAnnualConferenceonComputerGraphicsandInteractiveTechniques. [S.L]:ACM, 1995: 351-358.

[11]VOLLMERJ,MMNCLR,MUELLERH.Improvedlaplaciansmoothingofnoisysurfacemeshes[C].//ComputerGraphicsForum.[S.l.]:BlackwellPublishersLtd, 1999: 131-138.

[12]DESBRUNM,MEYERM,SEHRODERP,etal.ImplicitFairingofIrregularMeshesusingDiffusionandCurvatureFlow[C]//Proceedingsofthe26thAnnualConferenceonComputerGraphicsandInteractiveTechniques. [S.l.]:ACMPress/Addison-WesleyPublishingCo, 1999:317-324.

[13] FLEISHMAN S, DRORI I, COHEN-OR D. Bilateral mesh denoising [J]. ACM Transactions on Graphics, 2003(22): 950-953.

[14] KAZHDAN M, BOLITHO M, HOPPE H. Poisson Surface Reconstruction [C]//[s.n.].Proceedings of the Fourth Eurographics Symposium on Geometry Processing Eurographics Association, 2006:10-11.

[15] KAZHDAN M, HOPPE H. Screened poisson surface reconstruction [J]. ACM Transactions on Graphics (TOG), 2013, 32(3): 61-70.

[16] 马晓泉. 三维激光扫描数据处理与曲面重建方法研究[D]. 上海：华东理工大学, 2013: 6-7. MA Xiaoquan. 3D laser scanning data processing and surface reconstruction method [D]. Shanghai: East China Institute of Technology, 2013: 6-7.

[17] 莫堃. 基于隐式函数的曲面重构方法及其应用[D]. 济南：山东大学, 2010: 5-13. MO Kun. Surface reconstruction based on implicit function and its application [D]. Jinan: Shandong University, 2010: 5-13.

[18] LORENSEN W E, CLINE H E. Marching cubes: a high resolution 3D surface construction algo-rithm [C]//ACM Siggraph Computer Graphics. [S.l.]: ACM, 1987: 163-169.

3-D reconstruction of carbon-fiber fabric surface from laser scanning points cloud

CHENG Jie1, CHEN Li2

(1.InformatizationCenter,TianjinPolytechnicUniversity,Tianjin300387,China;2.SchoolofTextiles,TianjinPolytechnicUniversity,Tianjin300387,China)

Automatic analysis and measurement of fabric surface is an important problem for textile enterprises. To solve this problem, this paper captured high quality and dense original points cloud of carbon-fiber fabric surface using 3-D laser scanning system by adjusting illumination, analyzing organization chart and selecting appropriate scanning scope. According to the distribution of the original points cloud, they are classified and preprocessed in different ways.Scale-independent screened constrains including points constrains and gradient constrains are interpolated in the energy equation of preprocessed points set. Ideal 3-D model of fabric surface is reconstructed. The experimental results show that the average error of the width of yarn which is measured on the model is 0.12 mm.

carbon-fiber fabric; 3-D laser scanning; denoising and filtering; 3-D reconstruction

10.13475/j.fzxb.20150203107

2015-02-20

2015-08-18

国家自然科学基金项目(11072175)

程杰(1979—)，女，讲师，博士生。主要研究方向为机器视觉、三维重建。陈利，通信作者，E-mail：chenli@tjpu.edu.cn。

TS 101.8

A